“限地价,竞配建”土地出让方式的理论分析与实证研究
赵 娅
(上海交通大学安泰经济与管理学院,上海200052)
1 引言
2010年12月,北京市政府和国土部门首次明确了“限地价,竞配建”①简单地说,在“限地价,竞配建”挂牌出让中,地方政府事先设定一个不公开的地价上限,竞标者按照升价拍卖规则进行竞价,在当前价格达到地价上限时,竞标者以此地价上限为底价,针对保障房的配建面积进行竞争,当最终只有一个竞标者尚未退出拍卖时,此竞标者获胜,支付地价上限,并按成交的面积配建保障房。由于对地价和保障房面积的竞争均遵循升价拍卖规则,且地价存在上限,在达到上限时即进入第二阶段,因此可将这一出让方式刻画为一个有限价的两阶段的升价拍卖模型。的挂牌出让规则,目的在于促进保障性住房②保障性住房包括经济适用房、回迁房、两限房(限价限面积)、公租房和廉租房。的建设并控制地价和房价[1]。此后,包括广州、杭州在内多个地市也纷纷开始尝试这一出让规则[2]。截至2011年底,北京市已经有18宗地块按照此规则成功出让。实施这一规则的关键在于如何设置合理的地价上限。自2010年12月20日开始,国土资源部正式启动溢价率超过50%的地块交易需在两日内上报的机制③见《关于严格落实房地产用地调控政策促进土地市场健康发展有关问题的通知》。。事实上,通过观察即可发现,目前设置的地价上限几乎都处于将溢价率维持在接近50%的水平。那么,在采用此地价上限时,这一出让规则能否达到预期的效果呢?针对这一出让规则,很多意欲购房者也担心开发商会将建设保障房的利润损失转嫁到普通商品房的房价上,这一担心是否有必要?在出让保障房建设用地时,还有一种常用的招标出让方式,本文称之为“定配建、竞地价”④在“定配建,竞地价”招标出让中,地方政府事先规定并公布保障房的配建面积,然后由开发商针对土地价格进行封闭式报价,出价最高者或得分最高者(综合评标中)获胜,支付自己报出的土地价格,并在土地开发中配建规定面积的保障性住房。由于综合评标招标方式的均衡策略较为复杂,为简单起见,本文仅考虑价高者得的招标出让方式,因此可将这一出让方式刻画为一价封闭式拍卖。,这种出让方式自2007年就开始应用在北京市土地市场上,且已成功出让数十宗地块。在“限地价,竞配建”挂牌方式出现之后,这种招标方式仍在使用。虽然这两种规则出台的初衷是相同的,但在现实中,这两种出让方式是否收到了同样的效果呢?
针对上述问题,本文将“限地价,竞配建”规则刻画为设有限价的两阶段拍卖模型,并假设地方政府在追求土地出让收入的同时还会关注保障房建设带来的社会福利,在标准假设下讨论开发商的竞价策略和地方政府设置地价上限时的最优选择。对于多阶段拍卖模型,理论界已有很多研究,但都假设所有阶段的竞争针对同一目标即价格展开,例如Brisset和Morand[3]、Ye[4]、以及Perry和Wolfstetter[5],而本文的两阶段模型则围绕价格和保障房的面积展开。另外,本文考虑的两阶段拍卖模型与多属性拍卖也有类似之处。Che[6]和Branco[7]以及其他众多讨论多属性封闭式拍卖模型的研究都指出了评分规则在模型设计和现实执行中的重要性。当评分规则是特定的分段函数时,本文中的两阶段拍卖模型与多属性拍卖模型是等价的,这与David等[8]得到的结论是类似的。但目前使用的“定配建,竞地价”招标方式与之并不等价,本文的理论和案例分析均表明在保证建设相同面积的保障房时,招标的地价更低;挂牌的地价虽高,但通常能促使开发商建设更多的保障房。
2 “限地价,竞配建”挂牌方式——设有限价的两阶段拍卖模型
2.1 规则描述与模型假设
假设在某个地块的挂牌出让中,有N个风险中性的竞标者参与竞价,N={1,2,…,n}。竞标者的个人价值v相互独立且服从[v,v]上的同一分布F(·),密度函数为f(·)。拍卖设起始价r。在竞价的第一阶段,开发商针对土地的价格p出价,当价格达到地价上限M时,若至少有两个开发商愿意继续竞价,挂牌进入第二阶段,针对保障房的配建面积S竞价。若第一阶段的出价达不到M,则最后退出拍卖的开发商获胜,并按当前价格支付土地出让金。假设在保障房建成之后,地方政府要按照一定的价格进行回购,定义θ∈(0,1)为周边房价与保障房的价格之差与周边房价的比值,因此可将θ视为建设单位面积的保障房对开发商造成的损失,而地方政府回购单位面积的保障房需支出1-θ。假设地方政府在追求土地出让金的同时还会关注保障房建设对社会福利的改善,且其收益函数线性可加,即π=R+δS-(1-θ)S,其中δ为保障房建设对地方政府带来的边际收益,因此保障房面积S与土地出让收入R的权重分别为δ和1。除了每个竞标者的个人价值v为私人信息之外,其余均为公共信息。
2.2 竞标者的均衡策略
由于模型中的两个阶段都属于升价拍卖,根据拍卖理论,竞标者会在当前价格达到自己的个人价值时退出竞价,由此可得竞标者的均衡策略,如定理1和定理2所示。
定理1:在第一阶段中,竞标者的均衡出价策略为在当前价格达到p(v)=max{r,min{v,M}}时停止出价。
证明:由于第一阶段中设有限价M和起始价r,因此竞标者会在价格达到max{r,min{v,M}}时停止出价。
定理2:假设有K个(K≥2)开发商进入第二阶段,其在当前配建面积达到S(v)=(v-M)时退出竞价。
证明:在第二阶段中,价值为v的获胜竞标者报配建租赁房的面积S,承担的成本θS,并支付地价M,由于竞标者在总成本θS+M达到v时停止出价,因此第二阶段中竞标者的均衡策略是在S=(v-M)时退出竞价。
2.3 地方政府的均衡策略
给定竞标者的均衡策略,作为出让方的地方政府在设置地价上限M时会最大化自己的期望收入,由此可得地方政府的均衡策略如定理3所示。
定理3:当开发保障房的边际收益低于土地价格上涨的边际收益时,最优的地价上限为M*=1.5r;当开发保障房的边际收益高于土地价格上涨的边际收益时,最优的地价上限M*=r;当开发保障房和土地价格上涨的边际收益相等时,最优的地价上限 M*∈[r,1.5r]。
证明:当开发商执行定理1和2中的均衡策略时,地方政府的策略是选择使自身期望收益最大化的地价上限。地方政府从土地出让中获得的期望收益为:
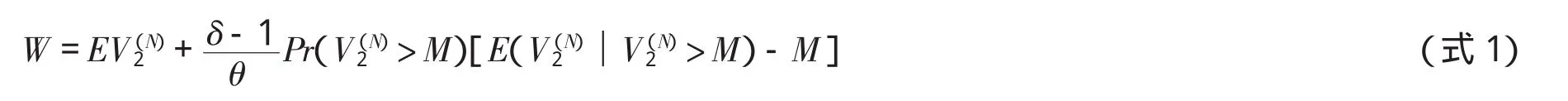
推论1:只有当建设保障房的相对边际收益δ由小于1上升到大于1时,地方政府才会降低地价上限。
推论2:如果能够使δ>1,地方政府的期望收益和整个社会的福利会同时达到最大值。
推论3:在δ>1时,提高保障房的回购价格可提高地方政府的期望收益和整个社会的福利。
证明:在δ>1时,提高保障房的回购价格意味着θ减小,由式1可知地方政府的期望收益会上升,同时保障房的建设面积也会增加,提高了整个社会的福利。

表1 以“限地价,竞配建”挂牌出让的3宗代表性地块的基本情况Tab.1 General characteristics of the three typical cases assigned by“controlling land price but bidding on providing public house”listing rule
推论4:“限地价,竞配建”方式为开发商带来的收益与普通挂牌方式相等。
证明:对开发商来说,建设保障房会损失一部分利润,但其支付的地价也更低。如果假设保障房和商品住房的开发成本相同,同一地块用普通挂牌方式和“限地价、竞配建”方式进行出让,开发商的事后收益分别为V1-V2和V1-M-θS。根据定理2,后者可简化为V1-V2。因此开发商不会将配建保障房带来的损失转嫁到商品房房价上,让全社会的购房者买单。
2.4 案例分析
为了对“限地价,竞配建”方式的理论结果进行验证,本文对2010—2011年间北京市土地市场上采用这一规则成功出让的18宗地块进行分析。表1中列举了其中3宗代表性地块的基本信息。
在2010年12月20日之前开始挂牌竞价的地块有7宗,其中最高报价低于地价上限的地块有3宗,另外4宗地块的报价则最终以竞投保障房配建面积成交,在这4宗地块中,有3宗地块的溢价率超过了50%,例如表1中的地块2。由可知1.5r<M*<V(2N),与保障房建设相比,地方政府更关注土地出让收入。
在2010年12月20日之后开始挂牌竞价的地块有11宗,其中4宗地块的最高报价超过了地价上限,以竞投配建保障房面积成交,而且这4宗地块的溢价率均低于但非常接近50%,例如表1中的地块3。这说明地方政府设置地价上限时显然以溢价率不超过50%为基础,即M*<1.5r<V(2N)。另外7宗地块的最高报价未达到地价上限,且溢价率非常低,有3宗地块甚至以起始价成交。根据推论4,土地价格的下降能够完全弥补开发商建设保障房的损失,因此在起始价不变的前提下,不存在“限地价,竞配建”方式抑制竞标者参与拍卖的可能,由此可推测,在实施溢价率超50%须上报的政策之后,地方政府提高了拍卖的起始价,以期能设定更高的地价上限。
综上,在18宗地块中有10宗地块的最高报价低于地价上限,虽然无法获得其地价上限的数据,但根据定理3,这10宗地块的地价上限M>max{r,V(2N)},表明δ≤1,这再次说明即使地方政府同时也注重保障房建设带来的社会福利,但仍无法超越其对土地出让收入的追求,而且在这种背景下“,限地价,竞配建”方式在现实中往往无法达到预期的成效。但是在异常交易须上报的政策辅助下,当1.5r<V(2N)时,地方政府设置的地价上限M*=1.5r可使开发商进入第二阶段,针对保障房面积进行竞争,从而达到控制土地价格,促进保障房建设的目的。而且,为了使这一出让方式发挥预期作用,除了异常交易须上报这一辅助政策之外,中央政府还必须对地方政府设定的拍卖起始价r进行限制,保证r<V(2N)①要获得V2(N)的数据,可利用北京市的普通挂牌出让的历史成交数据,对成交价格即次高个人价值进行建模,然后预测某个待出让地块的V2(N)。。
3 “定配建,竞地价”招标出让方式——封闭式拍卖模型
3.1 理论分析
在标准假设下,“限地价,竞配建”挂牌方式与特定评分规则下的第二评分招标方式是等价的。在评分规则为时,竞标者报出面积和价格(S,p)的组合,出让方根据报价组合计算每个竞标者的得分,分数最高者获胜。当次高分低于M时,获胜者支付得到次高分数的竞标者报出的价格;当次高分高于M时,获胜者支付自己报出的价格M,并按次高分的竞标者报出的面积建设保障房。
很明显,目前使用的“定配建,竞地价”招标方式与“限地价,竞配建”挂牌方式以及与之等价的招标方式并不相同。假设地方政府在以“定配建,竞地价”招标方式出让某个地块时,设定配建面积S0,有K个竞标者参与投标,其个人价值按大小顺序排列分别为V1,V2,…,VK,最终土地价格为p。如果此地块以“限地价,竞配建”挂牌方式出让,且获胜者也要配建保障房S0时,地方政府设定的地价上限为M0;假设地价上限为p时,最终保障房的配建面积为S。
定理4:当最高和次高竞标者的个人价值相差较小时,如果配建面积相同,招标地价低于挂牌地价;如果土地成交价格相同,挂牌出让的配建面积高于招标出让。
证明:在规定配建面积S0的招标出让中,竞标者相当于具有个人价值V-θS0,因此在一价拍卖中,竞标者的出价策略为当竞标者个人价值服从均匀分布时,招标出让的土地价格为如果挂牌出让中获胜者需要配建保障房的面积也是S0,那么θS0=V2-M0。比较p和 M0可发现,当 M0=(K-1)(V1-V2)时,p=M0;当 M0<(>)(K-1)(V1-V2)时,p >(<)M0。同理可比较 S 和 S0。
3.2 案例分析
为了对这一结论进行验证,本文对2010—2011年间北京市土地市场中以“定配建,竞地价”招标出让的地块进行分析。鉴于数据可得性的原因,本文仅选取样本期内的6宗地块。每个地块的数据包括地块的名称、所有竞标者的报价、房价损失θ、竞标者数量K、配建面积S、成交价格p、获胜竞标者的价值V1、次高价值V2、以及地价上限M0。利用定理4的证明中提出的均衡策略可计算获胜者的个人价值,在个人价值服从均匀分布,且有K个竞标者的情况下,获胜者的个人价值同理,利用第二高的报价数据可得到次高竞标者的价值V2,根据定理2中的均衡策略,即可计算相应的地价上限。表2中列出了6宗地块的计算结果。
如表2所示,所有地块的成交价格均低于普通招标方式下的土地价格,这说明“定配建,竞地价”招标方式既降低了土地价格,又带动了保障房的建设,与“限地价,竞配建”挂牌方式一样,都可作为促进保障房建设的重要手段。而且,6个地块中只有五里坨地块的招标价格高于地价上限,其余地块的招标价格均低于地价上限。五里坨地块的最高报价2.5×108元与次高报价1.588×108元相差了36%之多,而其余价高者得地块的最高报价和次高报价相差比例最高仅为3%。由此可验证定理4中的结论,而且现实中最高和次高竞标者个人价值的差别往往并不大,即竞标者之间的竞争较为激烈。

表2 以“定配建,竞地价”招标出让的6宗地块的计算结果Tab.2 The calculate results of the six cases assigned by“given fixed public house,bidding on the price of land”procurement rule
定理4说明,在一定条件下,地方政府可以通过在挂牌和招标方式之间进行选择,以实现控制地价或促进保障房开发的目的,而且表2中的案例分析表明这一条件在现实中通常是成立的。因此,若地方政府的主要目标是降低地价,招标方式是更好的选择;若主要目标是促进保障房建设,挂牌方式则要优于招标方式。
4 结论及政策启示
根据本文研究,当地方政府从保障房建设中获得的边际收益高于土地出让收入增加的边际收益时,无论从地方政府角度或全社会角度来看,“限地价,竞配建”的挂牌方式都要优于普通挂牌方式,因为其不仅能够控制土地价格,还有效激励了开发商对保障房的建设。中央政府可将保障房建设作为对地方官员政绩考核的一项重要指标,有效地激励地方政府在土地出中同时注重土地出让收入和保障房的建设规模。但这样一来地方政府从土地出让中获得的收入会大幅度降低,进而对地方政府的财政收支带来压力,因此中央政府在必要时需对积极实施这一出让规则的地方政府进行财政补贴。
更重要的是,如果能够对拍卖的起始价进行限制,在“溢价率超50%的地块交易须上报”这一政策的辅助下,“限地价,竞配建”挂牌方式可发挥预期的作用,实现中央政府控制地价并促进保障房建设的初衷。只有设定合适的起始价,地方政府以溢价率低于50%为标准设置地价上限时,才可保证开发商愿意针对保障房配建面积进行竞争。
“限地价,竞配建”挂牌出让与“定配建,竞地价”招标出让相比各有优劣,因此地方政府可根据中央政府在不同时期针对房地产市场采取的调控政策重点选择合适的出让方式。当降低地价为迫切之需时,地方政府应更多采用“定配建,竞地价”的招标方式;当促进保障房建设为政策目标时,“限地价,竞配建”挂牌出让则是一个更好的选择。随着政策重点的转向,“限地价,竞配建”的挂牌出让规则在北京市土地市场上应运而生。但与此同时,控制地价仍然是中央政府赋予地方政府的一项重要任务,因此从长期来看,这两种出让方式各有优势,将共同存在于中国的土地市场中。
(References):
[1]田青.加强保障房建设有利于调控房价[J].住房公积金研究,2011,(5):63-64.
[2]钟恺琳.广州试水“限地价、竞配建”[J].房地产导刊,2011,(6):22-23.
[3]Brisset K.,Morand P.H.Multistage auction with endogenous entry:a rational for B2B auction practices[J].Working paper,University Do Porto,2005.
[4]Ye L.Indicative bidding and a theory of two-stage auctions[J].Games and Economic Behavior,2007,58:181-207.
[5]Perry M.,Wolfstetter E.A sealed-bid auction that matches the English auction[J].Games and Economic Behavior,2000,33(2):265-273.
[6]Che Y.K.Design Competition through Multidimensional Auctions[J].The RAND Journal of Economics,1993,24(4):668-680.
[7]Branco F.The Design of Multidimensional Auctions[J].The RAND Journal of Economics,1997,28(1):63-81.
[8]David,Azoulay-Schwartz,Kraus.Bidding in sealed-bid and English multi-attribute auctions[J].Decision Support Systems,2006,42:527-556.

