开式弹链脱弹力分析

刘演龙, 王 雷

(1.海军驻重庆地区军事代表室,重庆 401120;2.海军驻西安地区军事代表室，陕西 西安 710043)

1 工作原理

根据自动炮的进弹方式不同，弹链节可分为开式弹链和闭式弹链两种。闭式弹链节的抱弹部的横截面为包角接近360°的圆环，炮弹只能从后方取出；开式弹链节的抱弹部不封闭，炮弹能够从前方、下方或后方3个方向取出。在当今高射速自动炮中，通常采用开式弹链，纵向脱弹方式，以减小自动机后坐距离，缩短自动机循环时间，达到提高射速的目的，一般炮弹是从弹链下方(纵向)脱出[1-2]。弹链节的脱弹力的大小将会影响到炮弹在脱弹时的难易程度。对于内能源自动炮来讲，脱弹力大小的选定尤为重要，脱弹力过大，在脱弹过程中将过多的消耗自动机的能量，降低自动机的后坐与复进速度，影响火炮的射速，甚至影响火炮射击的连发性能；在供弹线路复杂、供弹线路长的供弹系统中，弹链必须具有足够大的脱弹力，以保证在供弹过程中不因链带的抖动而使炮弹发生脱落或移位。在某型舰炮的研制过程中，为保证舰炮射速的实现，减小自动机的阻力，弹链脱弹力就选定较小，但该舰炮供弹系统线路长而复杂，射击试验时就多次出现炮弹从弹链内脱落的故障，严重影响舰炮功能的实现。由此可见在弹链的研制过程中，对弹链节脱弹力的研究是十分必要的。

2 开式弹链的脱弹过程分析

2.1 弹链力学模型

为了便于从理论上分析开式弹链的脱弹过程，可把弹链节简化为开口圆弧形曲杆。曲杆的截面为矩形，其高度t等于弹链节厚度，宽度b沿曲杆长度方向递变。弹链节在自由状态时半径为R，脱弹过程中弹链节开口逐渐张大(如图1所示)。

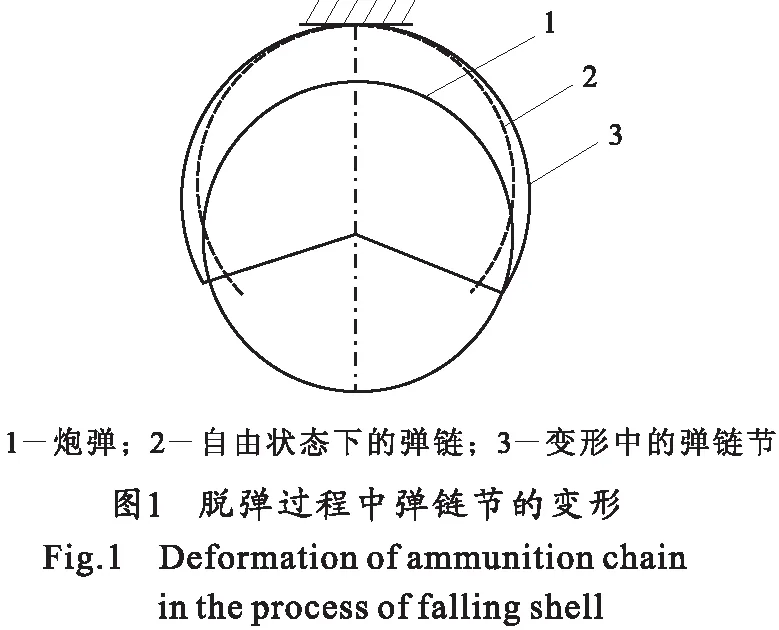
当弹链从静止抱弹状态开始到脱弹结束，炮弹对弹链抱弹部施加一定的载荷，弹链抱弹部将产生弯矩[3]。为了便于研究，现可将脱弹过程中作用在弹链节单边上的力转化为其自由端的一个集中力P和切向力f，且P始终通过自由端曲率圆中心。由于弹链节截面为对称y轴的一段圆弧，所以取一边圆弧来分析不影响研究结果。

2.2 力学特性分析

如图2所示，取曲杆上任一段AB，当在B端施加力P和FQ时，曲杆各段都发生了弯曲变形，最终累计到B点，使得B点产生位移，因此可认为在B段施加力P和f时，OA段进行弯曲变形后AB段再以A′点为定点进行了弯曲变形，最终整个曲杆达到了弯曲变形后的平衡。

2.3 建立曲杆的微分方程

曲杆弯曲变形平衡后，取曲杆上任意微段AB(如图3所示)，N、Q和M分别为曲杆的法向力、切向力和弯矩。

将作用在微段上的力分别向微段变形后的切向和法向投影，建立平衡方程，并以A点为矩心建立力矩平衡方程：

(N+dN)cosφ-N-(Q+dQ)sinφ=0

(1)

(Q+dQ)cosφ-Q+(N+dN)sinφ=0

(2)

(3)

式中：k为dθ段曲杆的曲率;φ为该微段变形后的曲率圆弧对应的圆心角，由于曲杆发生了纯弯曲变形，即在弯曲变形过程中没有拉伸变长，所以就有:

(4)

根据以上分析，略去二阶以上微量，得到曲杆平衡方程组如下：

dN=QRkdθ

(5)

dQ=-NRkdθ

(6)

dM=QRdθ

(7)

2.4 建立物理方程

对于薄曲杆，横截面上弯矩与曲率k之间的关系可用直梁平面弯曲理论来建立，由于弯矩使得曲杆曲率变小，于是该曲杆弯曲变形的物理方程为：

M=-EIk

(8)

式中：I为曲杆截面的轴惯性矩；b0为弹链节端点处的宽度；kx为弹链节宽度的变化率；E为弹链节材料弹性模量；t为弹链节材料厚度。

(9)

因为ΔMi是造成第i段弹性变形的力矩，那将式(7)代入整理得：

(10)

2.5 脱弹过程分析

2.5.1 脱弹过程力学分析

由于弹链节变形的对称性，可将半个弹链节简化为一端固定，另外一端支承在固定点的阶梯形圆弧曲杆，如图2所示。脱弹时炮弹对弹链节作用了力P和f，将弹链节横截面分为若干微段，每一微段变形前所对应的圆心角为Δθ，根据(5)、(6)、(7)式可知弹链节上第i段AB都有：

ΔNi=Qi-1RkiΔθ

(11)

ΔQi=-Ni-1RkiΔθ

(12)

ΔMi=QiRΔθ

(13)

又有：

Ni=Ni-1+ΔNi

(14)

Qi=Qi-1+ΔQi

(15)

式中：i=1，2，…，n。N0=f=Pu,Q0=P

又由式(10)可知：

(16)

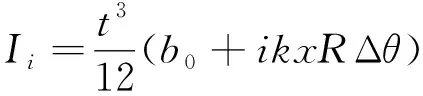
2.5.2 脱弹过程几何分析

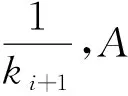
根据弹链节在坐标系中的位置及三角关系可求的B点坐标(xB，yB)：

当xA=xoi+1时，AOi+1为铅直线：

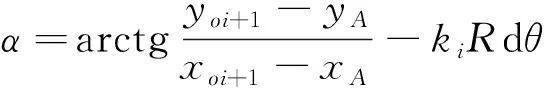
采用这种计算方法，可从固定点开始，逐渐推算到端点的坐标(xD，yD)，其中yD就是脱弹过程中弹链开口尺寸的二分之一。

当yD≥R时，可认为脱弹过程结束。

2.6 脱弹力

如图5所示，将P和f投影到水平方向上，则有：

即：F=2Psinαi+2fcosα1=2P(sinα1+ucosα1)

其中F为与脱弹力方向相反、大小相等的力，α1为弹链节末端的倾斜角。根据前面的分析可知：给定一个P值就能唯一确定一组k值，这组k值唯一确定了弹链节在P的作用下平衡后的几何状态，即确定了α1(具体值可根据弹链节计算过程中的最后两点的坐标求得)和一个脱弹过程开口尺寸2yD；而P与α1最终确定了脱弹力F，显然脱弹力F与弹链节脱弹过程开口尺寸2yD是一一对应的，因此可改变P来求得整个弹链脱弹过程中F和yD的关系。

3 算 例

以某型舰炮弹链为例，将弹链结构参数和最大弹带阻力P代入上节计算程序中进行脱弹力F计算，并改变该弹链的开口尺寸和弹链材料厚度，计算结果绘成曲线示于图6和图7中。

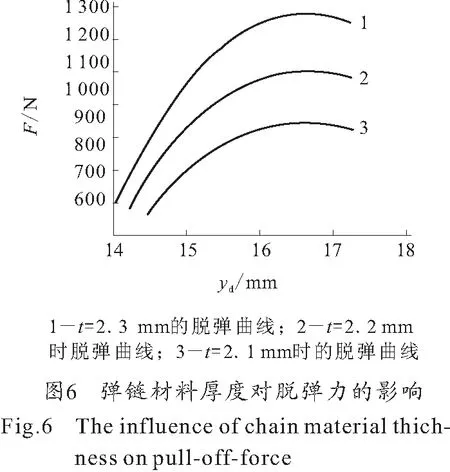
由图6和图7可以看出，弹链材料壁厚越大，脱链力越大，弹链开口尺寸越小，脱链力越大。

为验证理论计算的正确性和解决射击时弹链掉弹的故障，采用调整弹链的开口尺寸，弹链的其他有关参数保持不变的方法，将弹链前爪脱弹力从600～900 N提高到1 000 N以上，整体脱弹力从1 800 N提高到2 100 N以上。理论计算和实测数据对比如表1所示。

表1 某型弹链开口尺寸调整前后前爪脱弹力对照表

4 结束语

本文从定性和定量两个方面对开式弹链的脱弹过程进行了详细的理论分析，得出了影响弹链脱弹力的两个重要因素(厚度和开口尺寸)，并结合某型舰炮研制中为解决弹链掉弹故障，通过改变弹链材料的厚度和弹链的开口尺寸来调整弹链的脱弹力，进行了详细计算，计算结果为该型弹链的研制提供了重要的理论支持，在实践中采用改变弹链开口尺寸的方法，其实践结果与理论计算相吻合，圆满的解决了某型舰炮研制中出现的掉弹故障，同时这种研究方法为同类型开式弹链的研究提供了理论依据。

[1] 戴成勋. 自动武器设计新编[M]. 北京：国防工业出版社，1990:35-38.

DAI Cheng-xun.The newly organized of automatic weapon design[M]. Beijing:National Defense Industry Press,1990:35-38. (in Chinese)

[2] 马福球，陈运生，朵英贤.火炮与自动武器[M].北京：北京理工大学出版社，2003:76-83.

MA Fu-qiu，CHENG Yun-sheng，DUO Ying-xian.Gun and automatic weapone[M]. Beijing: Beijing Institute of Technology Press,2003:76-83.(in Chinese)

[3] 刘鸿文.材料力学[M]. 北京：高等教育出版社,2004:187-193.

LIU Hong-wen. Mechanics of materials[M].Beijing:Higher Education Press,2004: 187-193.(in Chinese)