某自行高炮波导缝隙天线仿真研究

范 薇，丁天宝，余继良

(西北机电工程研究所，陕西 咸阳 712099)

在对某自行高炮搜索雷达天线电磁环境进行分析时，搜索雷达天线建模是极其重要的。而波导缝隙天线阵是搜索雷达天线的关键技术。

波导缝隙天线阵具有结构紧凑辐射效率高、功率容量大和可靠性高等优点，在微波毫米波应用性系统中得到广泛应用。但是由于波导缝隙的相关结构参数计算比较复杂，从而增加了波导缝隙天线阵列设计的难度和成本。波导缝隙天线阵的设计方法通常有两种：一种是实验测量方法，另一种是理论计算方法。实验测量法具有设计简单和计算量小等优点，但需要加工多个缝隙进行测量且对测量系统要求很高，再加上缝隙尺寸的精度要求使得加工成本较高。理论计算方法主要是基于Elliot理论，利用各缝隙的各单元缝隙的自导纳和缝隙间的互耦阻抗、归一化导纳等约束条件求解天线的结构参数。理论计算方法对于较复杂的波导缝隙天线，由于其缝隙较多，使得仿真计算时间过长甚至无法实现天线的仿真。

笔者在本文中，提出了利用偶极子阵列天线代替波导缝隙天线进行仿真，求得天线远场方向图。相比其他分析方法，求解过程简单明了、物理意义清晰，具有计算量小和仿真速度快等优点。最后采用该方法仿真了工作频率为10 GHz的4单元矩形波导缝隙天线，仿真结果表明该方法比较有效。

1 缝隙天线理论基础

缝隙天线是开在薄金属板上的开槽天线，根据巴俾涅原理，金属板上的缝隙天线可用一个互补(对偶)的偶极子天线来分析。因此运用偶极子代替缝隙将得到缝隙天线的辐射场[1]。缝隙天线及其互补的偶极子如图1所示。

若在缝隙中心处加上电压源V0，则在缝隙口面就形成垂直于长边的电场分布Es(Z)，口面电场近似为正弦分布。

(1)

式中：Esm=V0/W,W为缝隙宽度；l为缝隙长度；β为波导内基模的传播矢量。

磁流线密度为：Jm=-n×Es，

对这样的缝隙天线，有一个互补的偶极子天线与之对应。偶极子的辐射电场表示如下:

(2)

式中:j为虚数单位；r为空间任一点的位置矢量；exp(-jβr)表示空间的相位变化；θ为传播矢量β与坐标轴z的夹角；η为媒质的特性阻抗;下标d表示dipole偶极子。

设在偶极子电流波腹Idm处的切向磁场为Hdm，由安培环路定律得:

Idm=∮Hdmdl=2HdmW

则得:

(3)

由电磁对偶关系可得缝隙天线产生的磁场为:

(4)

缝隙天线产生的电场为:

(5)

式中，Es m是缝隙口面上电场腹点值，因是细缝(W≪l),在Es m处的电压为V0=Es mW。

由式(3)和(5)可见，波导缝隙天线的方向图与对偶的偶极子方向图相同。

通过以上公式的推导，在理论方面，充分验证利用偶极子阵列仿真分析波导缝隙天线是正确的。

2 矩形波导缝隙天线仿真模型

2.1 基于Elliot理论对矩形波导缝隙天线建模

本文主要采用CST的微波工作室(MWS)对一个单根波导缝隙天线进行建模和仿真，波导内截面尺寸为a=22.86 mm,b=10.16 mm,波导壁厚t=1 mm，裂缝宽度W=1 mm。本文仿真的单根波导缝隙天线有4个单元，缝隙之间的距离为1/2λg(λg为波导波长)；辐射波导短路板离最近的辐射缝隙距离为1/4λg，基于Elliot理论,采用泰勒口径分布进行馈电，各个缝隙等幅激励[2-4]。经过计算求得各个缝隙单元的缝隙偏置和谐振长度，计算结果如表1所示。

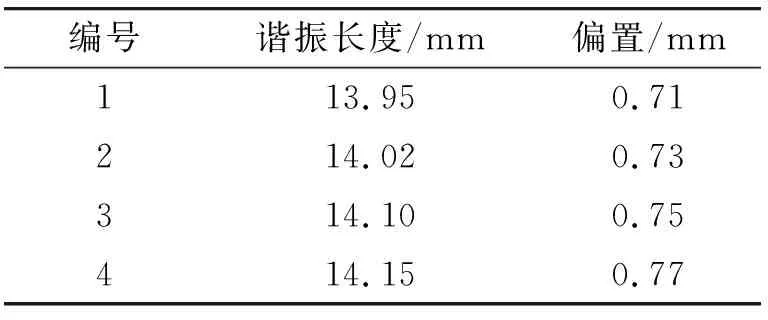
表1 4单元波导缝隙天线缝隙的谐振长度及偏置距离

根据以上数据在CST微波工作室中建立矩形波导缝隙天线仿真模型，其三维立体效果图如图2所示。

2.2 基于偶极子阵列对矩形波导缝隙天线建模

基于缝隙天线理论基础，运用偶极子代替矩形波导缝隙天线中的各缝隙建立偶极子阵列模型，此模型等效于矩形波导缝隙天线模型。偶极子及偶极子阵列仿真模型如图3所示，这个天线阵列有4个偶极子单元，每个阵列单元长为l=0.5λ，半径a≪λ，λ为有效波长，该阵列的阵列单元平行于z轴放置，阵列单元之间的间距与上述4单元波导缝隙天线缝隙间的距离相同[5]。

3 仿真与结果分析

3.1 波导缝隙天线远场方向图仿真

在4单元矩形波导缝隙天线仿真模型中，波导壁为理想电导体，端口采用波导端口，馈电方式采用端馈，仿真频率为10 GHz。对模型进行仿真计算，得到远场方向图如图4所示。

3.2 偶极子阵列天线仿真计算

对上述已建立的阵列天线仿真模型，在相同的CST环境中(仿真频率为10GHz)将各个偶极子端口设为离散端口并以高斯脉冲信号激励，偶极子端口阻抗与波导缝隙阻抗相同都为50 Ω。仿真得到天线远场方向图如图5所示。

3.3 仿真结果分析

由图4和图5可以看出，在相同的电磁仿真环境下，偶极子阵列天线E面、H面远场方向图与波导缝隙天线E面、H面远场方向图基本一致。差别只是偶极子阵列天线远场增益为12.78 dB,波导缝隙天线远场增益为12.08 dB。波导缝隙天线远场增益小于偶极子阵列天线远场增益0.7 dB，这是因为矩形波导缝隙天线辐射缝隙的导纳计算存在误差，以至于缝隙的谐振长度未达到优化程度。通过结果分析可知，运用偶极子阵列天线代替波导缝隙天线这个方法是可行的。

3.4 该方法在工程上的应用体现

从上述4单元波导缝隙天线和偶极子阵列天线的仿真结果可以看出，采用该方法获得两天线的远场方向图是一致的。因此，本文继续采用该方法仿真分析一个4×4的波导缝隙阵列天线，仿真结果充分说明该方法运用在复杂波导缝隙阵列天线建模中是可行的。

3.4.1 波导缝隙阵列天线仿真

根据前面设计的由4个缝隙单元组成的单根波导缝隙天线理论和仿真结果，在CST微波工作室中建立4×4的面阵天线。图6、图7分别表示波导缝隙阵列天线和偶极子阵列天线。对波导缝隙阵中每根缝隙天线一端进行馈电，仿真频率为10 GHz，不考虑阵列之间的互耦影响，仿真得到远场方向图，如图8(a)所示。偶极子阵列天线在相同的CST环境中，将各个偶极子端口设为离散端口并以高斯脉冲信号激励，得到远场方向图如图8(b)所示。

通过上述两阵列天线初步仿真的结果，可以看出，偶极子阵列天线与波导缝隙阵列天线的远场增益仍相差0.7 dB。因此，验证了在复杂波导缝隙阵列天线建模仿真中，运用这个简化方法在一定误差范围内可以得到高效、正确的结果。

4 结 论

本文提出了一种新的计算波导缝隙天线远场方法。通过对矩形波导缝隙表面电流的合理假设得到缝隙阻抗，将缝隙天线看作偶极子的连续阵进行仿真分析。本文采用CST微波工作室(MWS)分别对矩形波导缝隙天线、偶极子阵列天线的远场方向图进行了仿真分析，结果显示：两种天线模型仿真得到的远场方向图基本一致。由此说明，利用偶极子阵列模型仿真分析矩形波导缝隙天线不仅能够满足波导缝隙天线的辐射特性，而且可以大大降低建模过程的复杂度，并且能很好地满足工程应用的需求。该方法也可用在工程上后续的一些电磁兼容问题中。它为下一步搜索雷达天线建模提供了有力依据，从而为某自行高炮搜索雷达天线电磁环境的仿真奠定了坚实基础。

[1] 杨儒贵.高等电磁理论[M].北京：高等教育出版社，2008：187-189.

YANG Ru-gui.Advanced electromagnetic theory[M].Beijing: Higher Education Press, 2008：187-189.(in Chinese)

[2] ROBERT S.ELLIOT.The design of slot arrays including internal mutual coupling[J].IEEE Trans.Antennas and Propagation,1986,34(9):1149-1154.

[3] SANGSTER A J, WANG H.Resonance properties of omnidirectional slot doublet in rectangular waveguide[J].Electronics letters, 1993,29(1):16-18.

[4] ROBERT S.ELLIOTT.Antenna theory and design[M].USA:Prentice Hall,Inc.,Englewood Cliffs,N.J.07632.1981:325-336.

[5] 杨莘元，廖艳苹，马惠珠，等.有限偶极子天线阵的特性研究[J].哈尔滨工程大学学报，2006.

YANG Xin-yuan,LIAO Yan-ping,MA Hui-zhu,et al. Research on characteristics of finite dipole arrays[J]. Journal of Harbin Engineering University，2006.(in Chinese)