基于概率分布的目标未来域解算模型

夏方超，姚 忠，王 雷

(1.西北机电工程研究所，陕西 咸阳 712099;2.海军驻西安地区军事代表室，陕西 西安 710043)

采用跟踪集火射击体制的传统高炮(舰炮)，在拦截末端高速机动目标时，因射击时间短，造成命中概率下降，同时要求火炮随动系统功率更大，以实现高速调炮。能在短时间内发射大量弹丸的超高射速弹幕武器，采用空域窗拦阻射击体制，可拦截末端高速机动目标[1]。空域窗拦阻射击体制的前提是对目标未来域的解算，笔者提出了一种基于概率分布的未来域解算方法。

1 未来域解算方法

目标未来点的解算误差是由观测设备的测量误差和火控系统的解算误差等诸多因素引起的，其中，火控解算误差主要为目标运动假设误差。本文主要研究观测设备为雷达时的测量误差。

1.1 雷达测量误差

雷达测量误差可分为系统误差和随机误差两类。理论上，系统误差在校准雷达时可以消除。随机误差系指因某种偶然因素引起的测量误差，又称偶然误差，一般不能消除。随机误差是影响雷达测量精度的主要因素[2]。

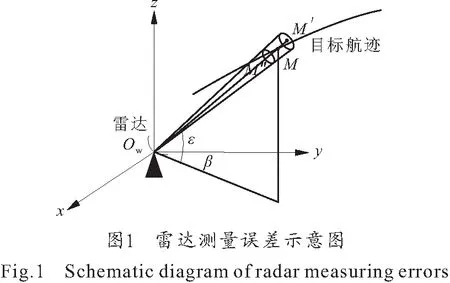
设t时刻雷达对空中某一目标进行测量时，目标视在位置为M(D,β,ε)，雷达测量误差的存在使得目标真实位置有以下情形：

1) 距离误差：目标斜距离的测量值为D，雷达的测距精度为±σD，则目标斜距离的真实值位于距离区间[D-σD,D+σD]内。

2) 方位角误差：目标方位角的测量值为β，雷达的方位角测量精度为±σβ，则目标方位角的真实值位于角度区间[β-σβ,β+σβ]内。

3) 高低角误差：目标高低角的测量值为ε，雷达的高低角测量精度为±σε，则目标高低角的真实值位于角度区间[ε-σε,ε+σε]内。

因此，t时刻雷达所给出的某被测目标的视在位置为点M，目标的真实位置则位于以M为中心，横截面为椭圆的圆台空域内，如图 1所示。

1.2 目标运动假设误差

目标未来点的预测与目标未来的运动规律有着极大关系。跟踪集火射击体制下，一般将目标运动规律假设为：等速直线运动或等加速运动[3]。跟踪射击的预测时间主要为弹丸飞行时间，预测时间较短；拦阻射击体制下的预测时间包括火控解算时间、调炮时间和弹丸飞行时间等，预测时间较长。针对上述问题，本文提出了一种多航路目标未来域解算方法：

1) 根据所要拦截目标的类型和所掌握的目标机动先验知识，确定目标最可能的攻击方式，将系统对目标位置、速度和加速度的预测误差转化为目标以一定概率飞行的多条航路。

2) 在不能确切获取目标特殊战术动作的情况下，建立能在一段时间内提供适当精度的目标运动描述。威尔斯特拉斯近似定理表明，多项式可在一个有限区间内以任何所需精度来近似一个连续函数。因此，本文提出采用多项式运动假设拟合目标未来航路。

2 目标未来域数学模型

本文的重点在于讨论目标未来域的解算方法，为简化数学模型，假设目标飞行方向朝向雷达。

2.1 飞行时间预测误差

以等加速运动模型为预测模型，将该运动模型下解算得到的目标未来点定义为理想未来点O，目标到达理想未来点O所用的飞行时间定义为理想飞行时间tO。目标提前或滞后到达理想未来点O的时间误差称为飞行时间预测误差。对目标飞行时间产生影响的主要因素有以下两方面：

1) 测量误差

在上述假设条件下，雷达测量误差中影响目标飞行时间的为测距误差±σD，该误差主要为随机误差[2]，测距误差近似地服从正态分布[3]，其引起的目标飞行时间预测误差ΔtL也近似服从正态分布，ΔtL可表达为:

(1)

式中:vT为目标速度;±表示目标提前或滞后到达理想未来点。

对于一维正态随机变量，其值落在区间[μ-3σ,μ+3σ]内的概率为0.997 4，可认为是肯定事件[3]，所以可确定目标飞行时间预测误差的数字特征为:

(2)

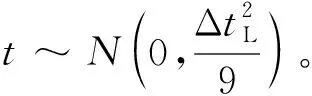
2) 运动假设误差

采用不同的目标运动假设，目标到达理想未来点的时间也不同。目标真实航路是由自动驾驶仪产生，末端航迹存在随机性[4]，该过程中的目标飞行时间预测误差可近似视为正态随机变量[3]，数字特征为:

(3)

ΔtH=|tO-max(ti)|

(4)

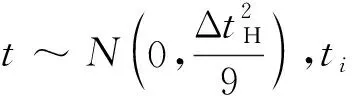
3) 飞行时间综合预测误差

测量误差和运动假设误差引起的目标飞行时间预测误差相互叠加。有限个相互独立的正态随机变量的线性组合仍然服从正态分布[3]，因此，目标飞行时间综合预测误差仍为正态随机变量，数字特征为:

(5)

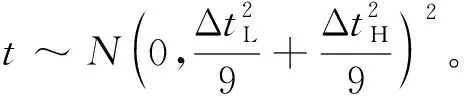
2.2 位置预测误差

目标到达预测迎弹面时的实际位置与预测位置存在偏差，称为目标位置预测误差，其影响因素如下：

1) 测量误差

测量误差中影响目标位置预测误差的为角测量误差，该误差为正态随机变量[2-3]，使目标真实位置分布在一椭圆区域内。设(xM,yM)为x坐标系下的目标视在位置，Sε、Sβ分别为散布椭圆的半轴长。目标位置预测误差为二维正态随机变量，数字特征为:

E(x)=xM,E(y)=yM

(6)

(7)

坐标变换对线段长度无影响，测量误差在目标视在位置处的线误差可投影到x坐标系内，故Sε、Sβ仍可表示为:

Sε=CmDσε，Sβ=CmDσβ

(8)

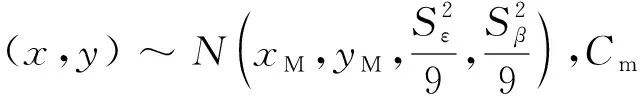
Cm=1.047 197×10-3(rad/mil)

2) 运动假设误差

3) 位置综合预测误差

如图 2所示，预测未来点Mi分布在以理想未来点O为中心的椭圆区域内，而目标真实位置又分布在以Mi为中心的椭圆区域内。加入测量误差，拟合预测迎弹面内目标可能出现的区域时，应主要考虑边缘未来点的测量误差[5]。

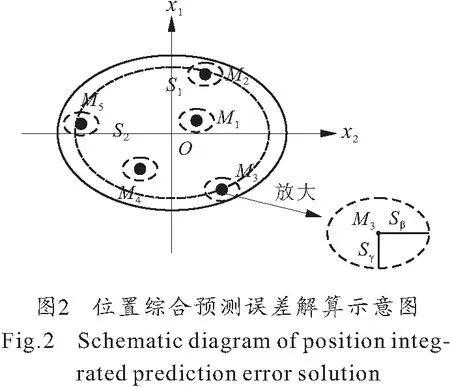
x坐标系中[5]，坐标原点为理想未来点O；x3轴为弹目相对速度方向；x1轴在弹目相对速度的铅垂面内，垂直于x3轴，方向向上；x2轴垂直于x1Ox3平面，方向取右手系，x1Ox2平面即为预测迎弹面。雷达测量误差在目标视在位置处的线误差，可直接与x坐标系下的未来点散布误差叠加。综合考虑所有情形，得到目标未来点最大散布区域：

(9)

目标未来点在该区域内的散布模型较复杂，为简化计算模型，本文将其等效为正态随机分布。

综上所述，目标未来域为被测目标所有未来点的集合。如图 3所示，目标未来点在时间上服从一维正态分布，主要分布在x3轴上；在空间位置上服从二维正态分布，主要分布在预测迎弹面x1Ox2内。因此，目标未来域为服从三维正态分布的时空域，可用三维正态分布的3σ等概率曲面所包含的空域描述，该空域为椭球域。

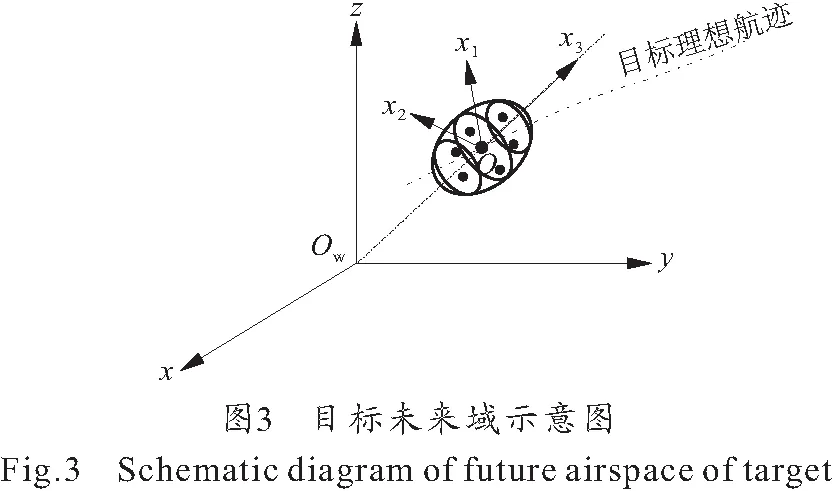
未来域数学模型可表示为：

(10)

目标未来点在未来域内出现的概率密度函数：

X∈[μ-3σ,μ+3σ]

(11)

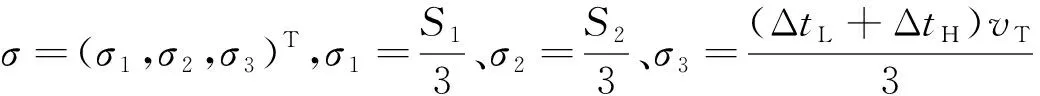
目标未来点落在未来域内的概率：

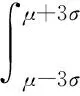
3 仿真实例

本文以某大口径火炮弹道为仿真目标，进行目标未来域的解算。设雷达在目标距离5.2 km处发现目标，并开始跟踪，拦截位置为目标距离1.026 km处，如图 4所示。以雷达开始跟踪时刻为仿真起始时刻，6 s后火控系统可解算出目标在拦截位置处的未来域参数，并将射击诸元发送到武器系统，指挥武器系统完成调炮和射击。

某雷达测量精度为[6]：距离±13.7 m；角度±1 mil。按照上述测量误差处理方法，可得到雷达测量误差引起的目标未来点散布误差，如表 1所示。

表1 雷达测量误差引起的未来点散布误差

雷达跟踪目标后，火控系统通过滤波和状态参数估值器获取目标运动参数，结合表 1中的方位误差和高低误差数据，可解算出目标在预测迎弹面内的位置综合预测误差，如图 5所示。

加入时间预测误差，即可得到拦截位置处的目标未来域参数，如表 2所示。

表 2 目标未来域参数

弹丸的未来域如图 6所示。

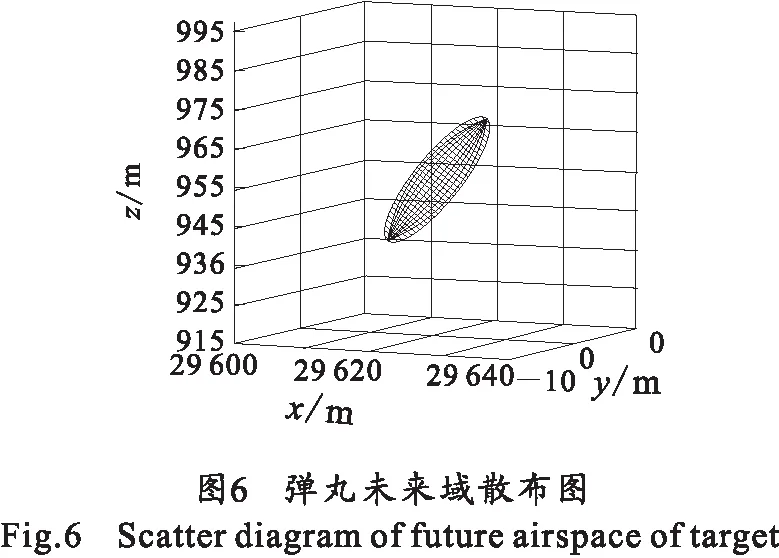
由图 5和图 6可以看出，非制导的射弹类目标末端弹道平滑，目标运动假设误差较小，未来点的散布误差主要为雷达测量误差。以上分析表明，目标未来域的大小与雷达的测量精度、目标的类型密切相关，雷达测量精度越高，目标机动性越差，火控系统对目标未来点的预测精度就越高，目标未来域也就越小。

4 结束语

本文提出了目标未来域的概念，基于概率分布的方法，分析了目标未来域的主要影响因素，给出了目标未来域的解算方法，建立了目标未来域的数学模型。以现有雷达测量精度为依据，得到了某大口径火炮弹丸的未来域模型。

[1] 王强，俞国庆，孙世岩,等. 拦阻射击下“金属风暴”武器系统的作战使用[J]. 兵工自动化，2008,28(9):7-10.

WANG Qiang, YU Guo-qing, SUN Shi-yan, et al. Combat employment of metal storm weapon system under interdiction fire[J]. Ordnance Industry Automation, 2008, 28(9): 7-10.(in Chinese)

[2] 丁鹭飞，耿富录. 雷达原理[M]. 西安：西安电子科技大学出版社,2002:170-270.

DING Lu-fei, GENG Fu-lu. Principles of radar[M]. Xi’an: Xidian University Press, 2002: 170-270. (in Chinese)

[3] 盛骤，谢式千，潘承毅. 概率论与数理统计[M]. 北京：高等教育出版社，1989：53-189.

SHENG Zhou, XIE Shi-qian, PAN Cheng-yi. Probability and mathematical statistics. Beijing: Higher Education Press, 1989: 53-189. (in Chinese)

[4] 刘兴堂. 导弹制导控制系统分析、设计与仿真[M]. 西安：西北工业大学出版社，2006：252-341.

LIU Xing-tang. The analysis,design and simulation of the missile guidance and control system[M]. Xi’an: Northwest Industrial University Press, 2006: 252-341. (in Chinese)

[5] 邢昌风，李敏勇，吴玲. 舰载武器系统效能分析[M]. 北京：国防工业出版社，2008：173-179.

XING Chang-feng, LI Min-yong, WU Ling. The analysis of ship-bone weapons system[M]. Beijing: National Defense Industry Press, 2008: 173-179. (in Chinese)

[6] 赵登平. 世界海用雷达手册[M]. 北京：国防工业出版社,2007：181-185.

ZHAO Deng-ping. Handbook of world marine radar[M]. Beijing: National Defense Industry Press, 2007: 181-185. (in Chinese)