六相感应电机的矢量控制研究*

屈 鲁，谢 卫，卢颖娟

(上海海事大学物流工程学院，上海 200135)

0 引言

六相感应电机调速系统由于具有低压器件实现大功率，转矩脉动减小，系统动、静态特性提高，可靠性提高，转子谐波损耗减小等优势，在电动汽车、船舰推进、航空航天等领域的研究与实践日益增加[1]。由于感应电机是一种典型的非线性、多变量、强耦合的控制对象，所以对其进行高性能控制十分复杂。

在三相感应电机调速系统中应用最多的高性能控制方案是:(1)按转子磁链定向的矢量控制系统;(2)按定子磁链控制的直接转矩控制系统。由于直接转矩控制系统调速范围不够宽，而矢量控制系统具有连续控制平滑和调速范围比较宽的优点，因此矢量控制仍是交流调速系统研究的重要方向之一。目前，矢量控制技术己被广泛应用于高性能感应电机调速系统中[2]。

1 六相感应电机的基本模型

1.1 六相感应电机的物理模型

六相感应电机的转子绕组仍为常见的笼型结构，定子绕组采用两组互差30°电角度的对称三相绕组构成的六相双Y型结构。若将笼型转子绕组也等效为类似的六相双Y型绕组，则六相感应电机的物理模型可用图1表示[3]。

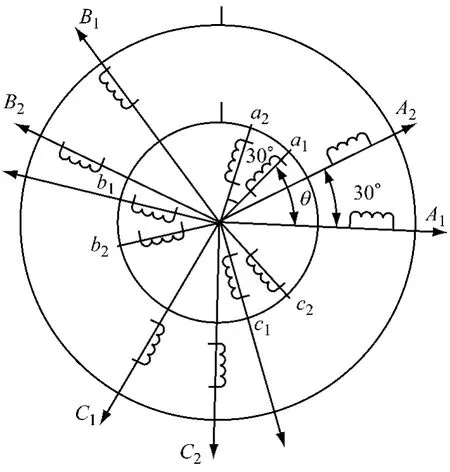
图1 六相感应电机的物理模型

1.2 六相感应电机的数学模型

六相感应电机在三相静止坐标系A-B-C下的数学模型是一个高阶、非线性、强耦合的多变量系统，可以通过坐标变换进行降阶、化简，由此建立六相感应电机在两相同步旋转坐标系d-q下的数学模型。

六相感应电机在两相同步旋转坐标系d-q下的磁链方程为

式中:Lm——d-q坐标系同轴定子与转子等效绕组间互感;

Ls——d-q坐标系定子等效两相绕组自感;

Lr——d-q坐标系转子等效两相绕组自感。

六相感应电机在两相同步旋转坐标系d-q下的电压方程为

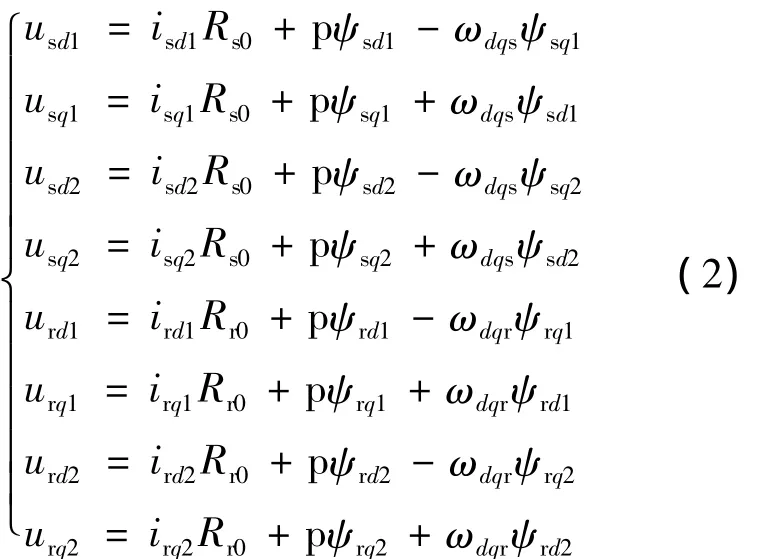
式中:ωdqs——d-q坐标系相对于定子 A1相的角转速;

ωdqr——d-q坐标系相对于转子a1相的角转速。

六相感应电机在两相同步旋转坐标系d-q下的转矩方程为

六相感应电机在两相同步旋转坐标系d-q下的运动方程为

1.3 六相感应电机的矢量控制方程

当采用定子电流、转子磁链及角速度作为状态变量，并按转子磁链定向时，即d轴沿着转子总磁链的方向且 ψrd1=ψrd2=ψr，ψrq1=ψrq2=0，从而可得六相感应电机基于转子磁链定向的矢量控制方程为

2 六相感应电机矢量控制模型

六相感应电机的矢量控制模型主要包括两个部分:定子电流的解耦模型和转子磁链的电流模型。

2.1 定子电流的解耦模型

由电磁转矩公式可知，电磁转矩仅由定子电流转矩分量isq1与isq2产生;由转子磁链公式可知，转子磁链仅由定子电流励磁分量isd1和isd2产生。从这个意义上看，定子电流的转矩分量与励磁分量是解耦的。

根据矢量控制基本方程，可以将六相感应电机的数学模型绘成图2所示的结构形式。由图可以看出，六相感应电机模型被分成ω和ψr两个子系统。

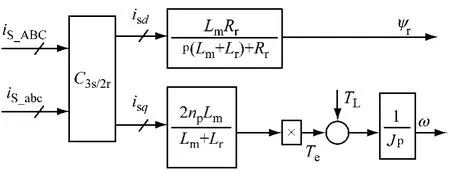
图2 六相感应电机定子电流解耦模型

2.2 转子磁链的电流模型

要实现按转子磁链定向的矢量控制，很关键的因素是要获得转子磁链信号，一般采用间接计算的方法。在计算模型中，由于主要实测信号的不同，转子磁链模型又分为电流模型和电压模型，此处选用电流模型。

图3是转子磁链电流模型的运算框图。六相定子电流经3/2变换，再经同步旋转变换并按转子磁链定向，得到两相同步旋转d-q坐标系上的电流，利用矢量控制方程式(5)可以获得ψr和ωs信号，由ωs与实测转速ω相加得到定子同步频率信号ωdqs，再经积分即为转子磁链的相位角φ，它也就是同步旋转变换的旋转相位角。

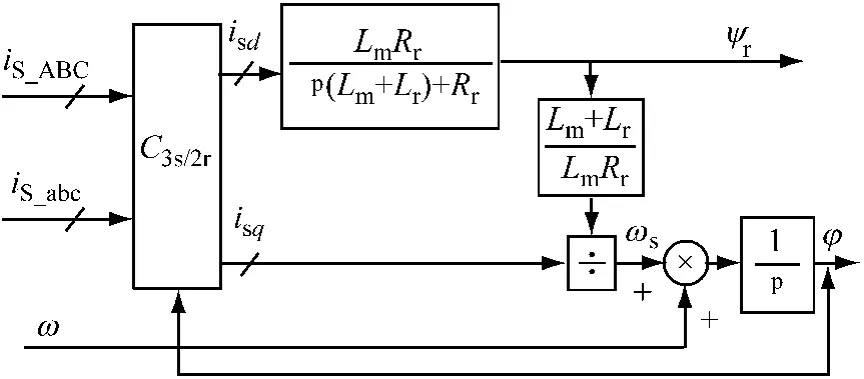
图3 六相感应电机转子磁链的电流模型

3 矢量控制系统调节器的设计

基于转子磁链定向的六相感应电机矢量控制系统，是一种带转矩内环的转速、磁链闭环的矢量控制系统。该系统分为转速控制子系统和磁链控制子系统[4-6]。

3.1 转速控制子系统

转速控制子系统设置了转速调节器ASR，只需要建立转速误差反馈，采用PI调节器，就可以得到如下参考转矩，即

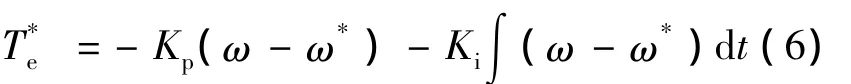
式中，Kp、Ki分别为比例增益和积分增益。转速调节器的输出T*e作为内环转矩调节器ATR的给定值，转矩反馈信号取自转子磁链观测器，其计算值为

只需要建立转矩误差反馈，采用PI调节器，就可以得到如下参考电流，即

设置转矩闭环的目的是，降低或消除两个控制子系统之间的耦合作用;另外，磁链一旦发生变化，相当于转矩内环的一种扰动作用，必将受到转矩闭环的抑制，从而减少磁链突变对转矩的影响。

3.2 磁链控制子系统

磁链控制子系统设置了磁链调节器AΨR，磁链的反馈信号来自转子磁链观测器。只需要建立磁链误差反馈，采用PI调节器，就可以得到如下参考电流，即

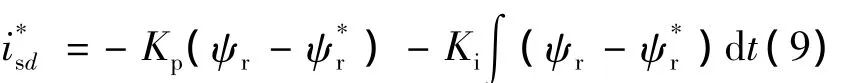
设置磁链闭环的目的是，控制转子磁链使其等于给定值，实现恒转矩调速。

综上所述，可以得到六相感应电机按转子磁链定向的矢量控制结构，如图4所示。

4 仿真分析

在MATLAB/Simulink环境下，建立六相感应电机矢量控制仿真系统。其中，六相感应电机的额定数据如下:np=3，f1=50 Hz，Rs=0.22 Ω，Rr=0.47 Ω，Ls=0.039 5 H，Lr=0.039 5 H，Lm=0.036 4 H，J=0.116 N·m2。负载转矩在 0.8 s时刻突变，由0 N·m→15 N·m;在1.4 s时刻突变，由15 N·m→0 N·m。

对建立的控制系统模型进行动态仿真，仿真得到转矩跟踪曲线、转速跟踪曲线和转子磁链跟踪曲线，分别如图5～图7所示。

图4 六相感应电机按转子磁链定向的矢量控制结构图

图5 转矩跟踪曲线

图6 转速跟踪曲线

图7 转子磁链跟踪曲线

从仿真波形可知:六相感应电机的实际转速和转子磁链可以很好地跟踪给定转速n*=1 000 r/min和给定转子磁链

5 结语

本文对六相感应电机按转子磁链定向的矢量控制进行了研究。在此基础上，设计了六相感应电机的转速控制子系统和磁链控制子系统，实现了定子电流的解耦和转子磁链的观测，并在Simulink中进行动态仿真。仿真结果证明了六相感应电机矢量控制系统能很好地跟踪速度、磁链给定，具有较好的动静态响应能力。

[1]庄朝晖，熊有伦，马挺.多相感应电机变频调速系统回顾、现状及展望[J].电气传动，2001(2):3-7.

[2]陈伯时.电力拖动自动控制系统[M].3版.北京:机械工业出版社，2003.

[3]ZHAO Y，LIPO T A.SVPWM control of dual threephase induction machine using vector space de-composition[J].IEEE Transactions on Industry Applications，1995，31(5):1100-1109.

[4]BOJOI R，LAZZARI M，PROFUMO F，et al.Digital field oriented control for dual three phase induction motor drives[J].IEEE Trans Ind App，2002(IA-02):818-815.

[5]KIANINEZHAD R，NAHID M B，BETIN F，et al.Sensorless field-oriented control for six-phase induction machines[J].IEEE Trans Ind App，2005(IAS-05):999-1006.

[6]BOJOI R，GRIVA G，PROFUMO F.Field oriented control of dual three-phase induction motor drives using a luenberger flux observer[J].IEEE Trans Ind App，2006(IA-06):1253-1260.