模糊控制在直线感应电机磁场定向控制中的应用
张云红, 曾成碧, 徐 伟, 肖先勇
(1.四川大学电气信息学院,四川成都 610065;
2.墨尔本皇家理工学院工程技术研究所,澳大利亚墨尔本 3001)
0 引言
单边直线电机(以下简称“直线电机”)轨道交通系统作为一种新兴的城市运输方式,从20世纪80年代起,已经应用于许多城市的轨道交通系统中,比如加拿大温哥华、日本东京、美国底特律、马来西亚吉隆坡以及中国的广州和北京等[1-2]。目前直线电机在各高校和企业都成为研究的热点。直线电机驱动系统结构简单,不靠轮和轨之间的摩擦力,而是直接依赖初次级间电磁感应原理所产生的水平推力,因此该系统具有很好的加减速性能和较强的爬坡能力[3-4]。但由于它相当于旋转电机沿半径中轴切开并水平展开,在其运行时,会产生纵向边缘效应,引起气隙有效磁通和牵引力系数降低[5]。所以直线电机的数学模型虽由旋转电机而来,但比其更加复杂。本文引用J.Duncan[6-8]提出的直线电机数学模型,它考虑了电机的纵向边缘效应,与实际情况相符。在此基础上,建立了直线电机转子磁场定向控制的仿真模型。传统PI控制器算法简单,稳定性高。但其基于线性系统设计,且参数固定,对于参数不断变化的直线电机,其控制性能会大打折扣[9]。模糊控制不依赖于控制对象的数学模型,能够模仿人的思维且将人的经验带入控制过程中[10-11]。文中将PI控制和模糊控制结合起来,设计了模糊自适应PI控制器,它能根据外部的变化,及时调节PI控制器的比例系数(KP)和积分系数(KI),使其适应外部环境。将此控制器用在仿真模型的速度环中。仿真结果表明,模糊自适应PI控制器能够克服控制系统的参数变化和非线性等因素,使其具有更快的速度跟踪能力,更强的抗扰性和更好的鲁棒性。
1 直线电机次级(转子)磁场定向控制原理
1.1 直线电机数学模型
根据旋转电机理论,本文建立了在次级磁场定向同步坐标系下的直线电机数学模型,主要总结如下[12]。
初次级电压方程:

初次级磁链方程:

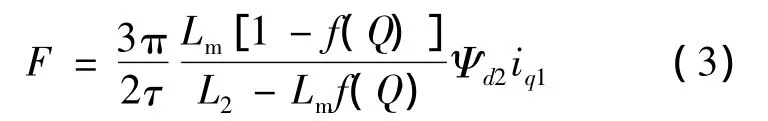
上述方程中的f(Q)为边缘效应量化函数,其表达式如下:

电机推力方程:
其中:ud1,uq1——分别为 d、q 轴初级电压;
Ψd1,Ψq1——分别为 d、q轴初级磁链;
Ψd2,Ψq2——分别为 d、q轴次级磁链;
ω1——同步角频率;
ω2——运动电角速度;
R1、R2——分别为初、次级电阻;
id1、iq1——分别为 d、q 轴初级电流;

Tv——初级通过空间一点的时间;
T2——涡流的衰减时间常数;
D——电机初级长度;v——电机线速度;ωsl——滑差频率。
1.2 磁场定向控制原理
磁场定向分为气隙磁场、定子磁场和转子磁场定向。由于气隙磁场和定子磁场定向控制方式复杂,本文采用转子磁场定向控制。

滑差频率方程:id2、iq2——分别为 d、q 轴次级电流;Lm——励磁电感;
Ll1、Ll2——分别为初、次级漏感;
τ——初级极距;
L2——次级自感;
p——微分算子;转子磁链角度方程:
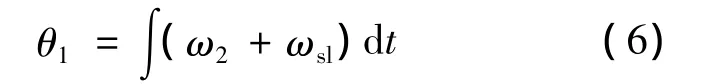
次级磁链方程:

2 仿真模型介绍
在MATLAB/Simulink中建立的直线感应电机磁场定向控制结构如图1所示。该模型包含一个速度控制的外闭环和两个初级电流控制的内闭环。外闭环采用模糊自适应PI控制器,两个内闭环采用PI控制器。逆变器采用SVPWM算法,直线感应电机的模型基于J.Duncan的数学模型。
PI控制是一种成熟的控制方法,并广泛应用于工业控制系统中,其控制原理如图2所示。比例调节能够按比例反应系统偏差,一旦系统出现偏差,它将立即作用以减少偏差。比例系数大,能够减少调节时间,但过大会降低系统稳定性,甚至造成系统不稳定。积分调节的目的是消除系统稳态误差。只要系统存在稳态误差,积分作用就一直进行,直至误差消除。积分系数越小,积分作用就越强。但引入积分调节使系统稳定性下降,动态响应变慢。

图1 直线电机磁场定向控制结构图

图2 PI控制器结构图
文中结合PI控制和模糊控制设计的模糊自适应PI控制器结构如图3所示。该控制器是一个双输入双输出的系统。输入为运动电角速度误差(e)和其误差变化率(ec),输出为ΔKP和ΔKI。
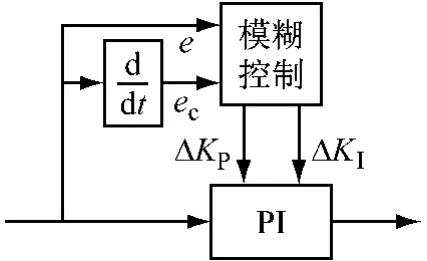
图3 模糊自适应PI控制器结构图
该控制器通过模糊控制器的输出ΔKP和ΔKI调节PI控制器的比例系数和积分系数,可表述为

式中,K'P和K'I为调整后的KP和KI。
模糊控制器的整个控制过程包括三个部分:输入模糊化、模糊推理和输出反模糊化,如图4所示。
(1)输入模糊化。如图4所示,E和EC为输入e和ec的模糊变量。设输入和输出的论域均为{-6,-5,- 4,- 3,- 2,- 1,0,1,2,3,4,5,6}。量化因子Ke和Kc用于模糊化输入变量,如式(10)所示:

(2)模糊推理。定义模糊集合为{NB,NM,NS,Z,PS,PM,PB},其隶属度函数如图 5 所示。NB和PB的隶属度函数分别为Z型隶属度函数,其余为三角形隶属度函数。

图5 输入输出的隶属度函数
专家建议或经验在模糊控制系统中被转换为控制规则。根据输入的模糊集合,该模糊控制器的输出均有49条控制规则,如表1和表2所示,且采用Mamdani模糊推理方法。Kp和KI的输出表面如图6和图7所示。
(3)输出反模糊化。Kp和KI为ΔKP和 ΔKI的模糊变量。ΔKP和ΔKI为系统输出的精确控制量。y1和y2为比例因子。反模糊化可描述为

表1 Kp的控制规则

表2 KI的控制规则
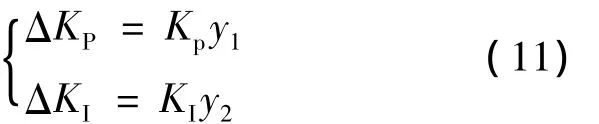

图6 Kp的输出表面
3 仿真结果和分析
模糊自适应 PI控制器的主要参数:Kp=0.06,KI=1,y1=0.1,y2=0.5。直线电机的主要参数如表3所示。

图7 Ki的输出表面

表3 直线感应电机主要参数
为比较PI控制器和模糊自适应PI控制器的性能,分别在两种情况下进行仿真:(1)电机空载起动至线速度为5.6 m/s,并在第5 s时突然停止运动;(2)电机带1 000 N负载起动至线速度为5.6 m/s,并在第5 s时突然停止运动。为简化分析,该仿真忽略空气和轮轨间等一切形式的摩擦力。
通过空载和带负载的直线电机线速度曲线可看出,在速度环采用模糊自适应PI控制器的直线电机控制系统中,电机起动时线速度能较快达到设定值(空载时,采用模糊自适应PI控制器和PI控制器的系统上升时间分别为 0.105 s和0.118 s;带负载时,分别为0.12 s和 0.127 s),说明该控制系统具有较好的跟随性能;电机制动时能较快停止且未出现超调和稳态误差。这是因为空载起动和突然制动相当于速度发生了突变,在模糊自适应PI控制器的调节下,速度环可以根据速度反馈量的变化大小和快慢,实时地修正其比例系数和积分系数,使其适应外界的变化,从而系统具有更好的抗扰性和鲁棒性,具体如图8和图9所示。

图8 空载时直线电机仿真图形
在两种工况下,电机推力在传统PI和自适应PI的调节下,其最后的变化曲线几乎重合。这是因为对于推力控制,电流采取了限流措施,以防止电机烧坏。在饱和的状态下,采用模糊自适应PI控制器的控制系统和采用PI控制器的控制系统的输出是一样的,都为电流限幅的上限;推力电流都采用相同的PI控制器,所以输出的推力电流相同,因此输出的推力也一样。励磁电感的曲线验证了励磁电感随电机速度的上升而逐渐衰减。
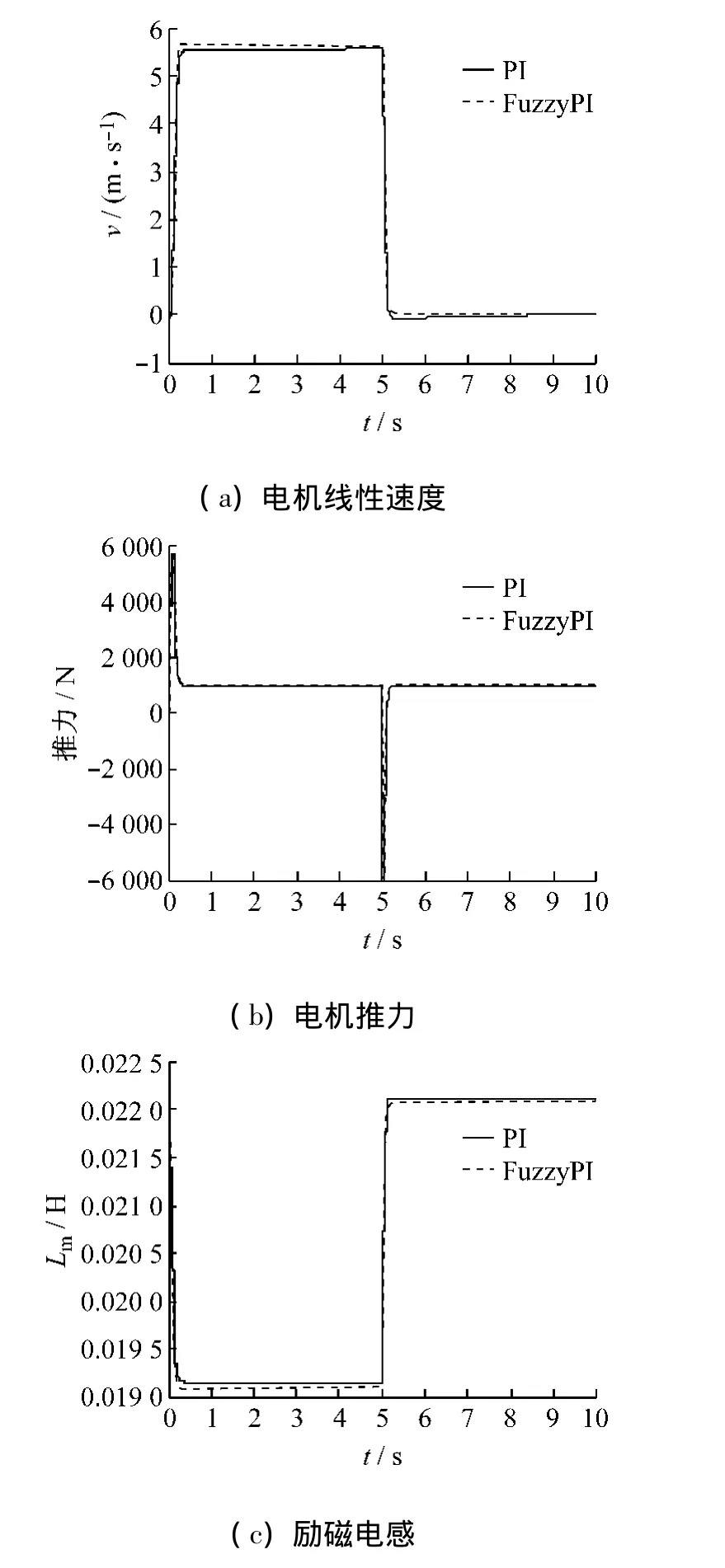
图9 带1 000 N负载时直线电机仿真图形
4 结语
本文结合PI控制和模糊控制的优点,设计了一种模糊自适应PI控制器,将其应用在直线电机转子磁场定向控制的速度环中。其中根据 J.Duncan对边端效应的直线电机互感的校正系数,本文利用MATLAB/Simulink中的模糊逻辑工具箱建立了模糊自适应PI控制器的仿真模型,并分别在空载和带载的情况下进行了仿真研究,并与传统的PI控制策略进行了对比。大量仿真结果表明:采用模糊自适应PI控制器的控制系统具有较好的跟随性能、抗扰性和鲁棒性。
[1]徐伟,李耀华,孙广生,等.交通用大功率直线异步电动机牵引特性[J].电工技术学报,2008,23(7):14-20.
[2]王珂,史黎明,何晋伟,等.单边直线感应电机法向力牵引力解耦控制[J].中国电机工程学报,2009,29(6):100-104.
[3]杨伟民,徐月同,陆华才,等.基于DSP的永磁同步直线电机无位置传感器控制系统[J].电机与控制应用,2007,34(4):28-32.
[4]任晋旗,李耀华,王珂.直线异步电动机的损耗模型与效率优化控制[J].电工技术学报,2009,24(12):68-73.
[5]潘霞远,刘希喆,吴捷,等.永磁同步直线电机的鲁棒PID控制[J].电机与控制应用,2008,35(9):34-38.
[6]DUNCAN J,ENG C.Linear induction motor-equivalent-circuit model[J].IEE Proceeding of Electrical Power Application,1983,130(1):51-57.
[7]W X,ZHU J G.An improved equivalent circuit model of a single-sided linear induction motor[J].IEEE Transactions on Vehicular Technology,2010,59(5):2277-2289.
[8]W X,ZHU J G.Equivalent circuits for single-sided linear induction motors[J].IEEE Trans Ind Appl,2010,46(6):2410-2423.
[9]TURSINI M,PARASILITI F,ZHANG D Q.Realtime gain tuning of PI controllers for high-performance PMSM drives[J].IEEE Trans Appl,2002,38(4):1018-1026.
[10]叶云岳,陆凯元.直线电机的PID控制与模糊控制[J].电工技术学报,2001,16(3):11-15.
[11]WAI R J,CHU C C.Motion control of linear induction motor via Petri fuzzy neural network[J].IEEE Trans Ind Electron,2007,54(1):281-295.
[12]任晋旗,李耀华,徐伟,等.直线感应电机在线参数辨识[J].中国电机工程学报,2008,28(24):113-117.

