论量子超光速性
黄志洵
(中国传媒大学信息工程学院,北京100024)
论量子超光速性
黄志洵
(中国传媒大学信息工程学院,北京100024)
A.Einstein对量子力学(QM)的反对态度从1926年开始显露,1935年与B.Podolsky、N.Rosen联合发表论文时达到顶点,而EPR论文后来是从反面促进了科学的发展。该文以狭义相对论(SR)为思想基础,而SR和EPR都否定超光速的可能性。但QM允许超光速存在,并与研究超光速的前提即QM非局域性一致。1985年John Bell说,Bell不等式是分析EPR推论的产物,该推论说在EPR文章条件下不应存在超距作用;但那些条件导致QM预示的奇特相关性。Aspect实验的结果是在预料之中的,因为QM从未错过,现在知道即使在苛刻的条件下它也不会错;可以肯定实验证明了Einstein的观念站不住脚。Bell认为在进退两难的处境下可以回到Lorentz和Poincarè,他们的以太是一种特惠参考系,在其中事物可以比光快。Bell指出正是EPR给出了超光速的预期。……1992年以来有多个超光速实验成功的报道,有的以量子隧穿为基础,有的利用经典物理现象(如消失波、反常色散)。而在2008年,D.Salart等用处于纠缠态的相距18km的2个光子完成的实验证明其相互作用的速度比光速大一万倍以上,为104c~107c;可以说此实验对有关EPR的长期争论作了结论。
过去25年来,量子超光速性是笔者的主要研究课题之一。1985年我们提出了量子势垒的等效电路模型;1991年我们最早指出截止波导中消失波模有负相速(vp<0)和负群速(vg<0)现象,笔者的专著《截止波导理论导论》获全国优秀科技著作奖。2003年我们用同轴光子晶体进行实验并观测到阻带中的超光速群速,为(1.5~2.4)c。2005年我们提出广义信息速度(General Information Velocity,GIV)和在2010年提出量子超光速性(Quantum Superluminality,QS)两个概念,并建议改造现有的高能粒子加速器以寻找和发现超光速奇异电子。本文则较深刻地讨论了QS的若干问题,涉及微观粒子的速度定义、EPR思维与超光速研究的关系、量子纠缠态作用速度、量子隧穿的超光速性、负波速、Casimir效应的超光速性。文中指出Sommerfeld-Brillouin波速理论的意义和不足,用实验例说明量子光学(QO)方法与经典物理概念结合运用是重要的。
自2000年以来的负群速实验常以某金属(如铯、钾、铷)的原子蒸汽状态作为受试对象,充分利用激光的高科技特性和手段,从而使之成为具有典型QO特征的现代物理实验,因而极不同于经典性质的物理实验。负群速不仅是超光速的特殊形态,而且普遍具有下述特征:输入脉冲进入媒质前,出口处即呈现输出脉冲峰,因而与经典因果性不同。
虽然关于QS的知识和发现是丰富的和生动的,并且极有启发性,但它并不正面和直接地回答“物质、能量、信息能否以超光速传送”的问题。设计巧妙而有说服力的实验仍是科学家们的基本任务。
量子力学;量子超光速性;量子纠缠态;量子隧穿;负波速;量子光学(QO)
(接上期)
6 量子隧穿的超光速性
量子理论中由E.Schrödinger[1]提出的描写粒子和波的运动方程(SE),其重要性类似电磁理论中的Maxwell方程。关于它,有一些流行的误解(例如说它只能在低速下使用),因此需要有所说明。1924年de Broglie根据电子说“粒子有波性”,认为能量E动量p的粒子入射时必带有一种波动(最早叫相波phase wave,后来叫物质波),1928年由电子绕射实验证实。de Broglie的论文对E.Schrödinger有很大启发,他尝试把物质波推广到非自由粒子方面,从而得到了一个简洁的解,能级以某种算符的本征值形式出现。这时Schrödinger立即把方法用到氢原子中的电子身上。他开始运用电子运动的相对论力学,但结果却与实验不符。几个月后他改用非相对论方法处理电子,得出的结果与观测相符。他最终写出了论文并在1926年上半年陆续发表。Schrödinger后来说,虽然在寻找波方程时“被迫放弃了相对论”,使他感到“不好意思”;但那时他不得不如此,因为引入相对论时发生了“大得惊人的困难”。
所谓含时的Schrödinger方程是他在1926年6月提出的,其形式为

(14)
=-▽2+U
(15)
得到

(14a)
这是含时Schrödinger方程的简明写法。




故有

(16)
这是不含时Schrödinger方程,它描写的状态是定态,E是能量本征值。因此,不含时的Schrödinger方程是能量算符的本征方程。
对Schrödinger方程应有全面的了解。首先,应区分自由粒子(不受力场作用)和非自由粒子(受力场作用)的不同情况。前者相当于U=0,其能量E(就是动能Ek)为

(17)
式中v、p为粒子速度和动量。在后一情况,能量~动量关系变了,应当是

(18)
所以两种情况是不同的。至于“含时”和“非含时”的区别,前者是说作用在粒子上的力场随时间t变化。但是在许多实际问题中,作用在粒子上的力场不随时间变,故有后一种情况(“非含时”方程);这时偏微分方程较易处理,用分离变量法即可变为求解常微分方程的问题。
不含时(定态)的SE可写为另一形式:
(19)

因此,认为SE只能在低速条件下使用的说法是错误的。我们并不反对RQM波方程(特别是Dirac方程),只是反对贬低SE。如照有的物理学家的说法,微观粒子将区分为两大类——低速运动粒子用Schrödinger方程,高速运动的粒子用Dirac方程。这不仅与事实不符,也是教条主义思维的反映(只因为SE是非相对论性的便作如是判断)。其实,说Newton力学方程在高速运动时便失效不能使用,至今也没有实验上的证明。实际上,当比较运动状态的演化规律时,与经典力学中的Newton定律对应的是QM中的SE;这就是Schrödinger工作的历史地位,至今无人能够撼动。


(20)
这是波函数归一化条件。无疑的,我们在写出上式时必定知道这指的是没有物质粒子产生或湮灭的物理过程。
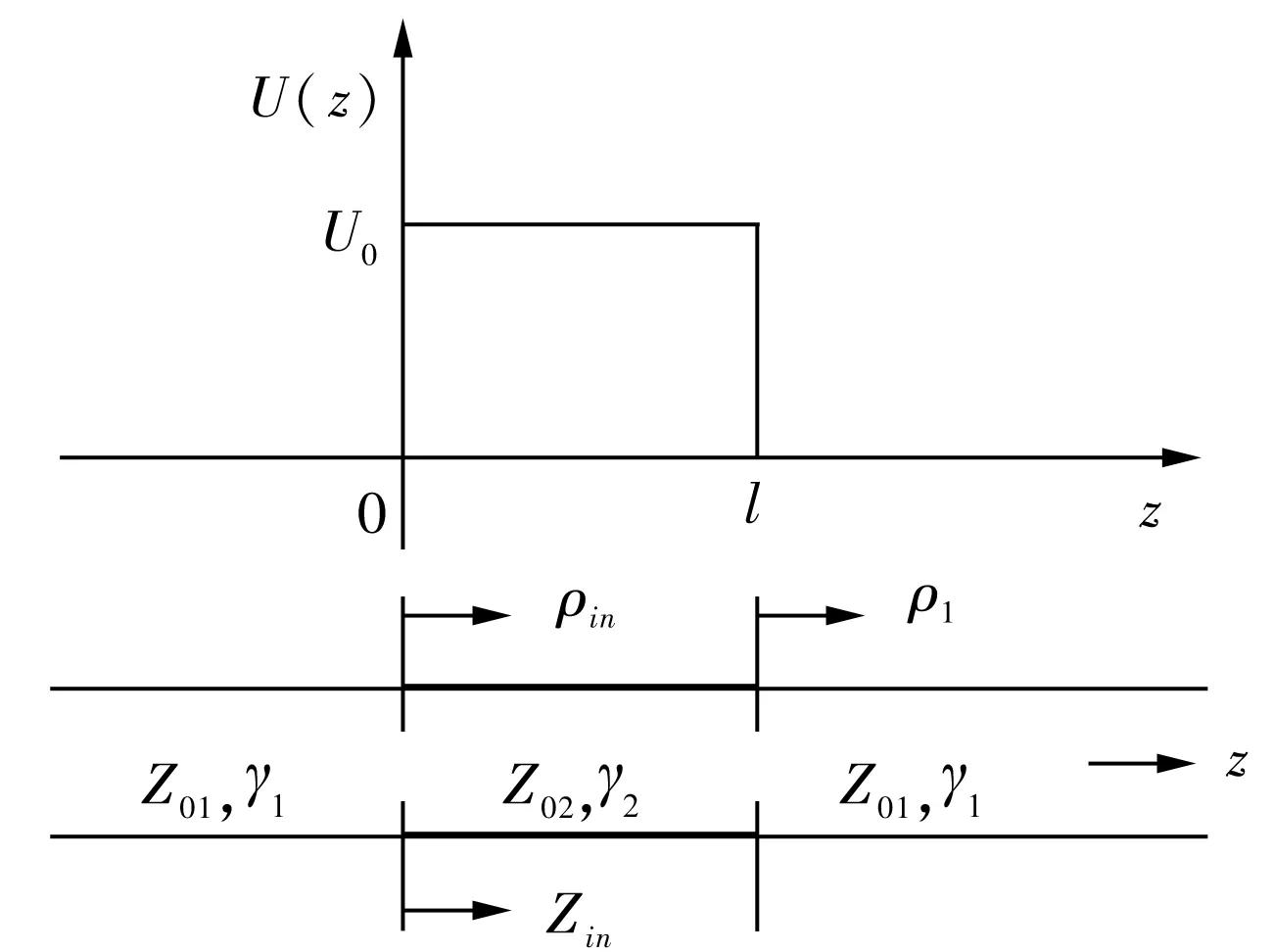
为了了解20世纪90年代以来的多个超光速实验,必须建立关于量子隧道效应和消失波效应的理论基础。考虑一个粒子沿坐标z方向作一维运动,途中遇到一个势能区域,宽度为l,高度为U0;假定粒子能量为E,而E 粒子在力场作用下射向一个矩形势垒时的分析:设垒高为U0,垒宽为l,入射粒子能量为E;设粒子运动方向为z方向,几率流密度算式为 (21) 式中ψ是波函数,h是Planck常数,m是粒子质量,z是粒子运动方向。J在垒内和垒外是不同的。垒外也分两种情况:入射端为Jinc,出射端为Jtr,后者表示传输的(透射的)几率流密度。考虑U0>E的情况,即垒高(能量)大于入射粒子能量;设粒子速度为v,按能量守恒有 (22) 这时(E-U0)<0,故有v2<0,v为虚数;这是不合理、不可能的,故一个经典力学中的粒子不可能到达势垒的右方。微观粒子则不同,按照QM中的不确定性原理(测不准关系式),不能同时得到粒子速度和坐标位置的准确值,即不能同时得到粒子动量和势能的准确值。故在垒内势能为已知的情况下,动能是不确定的。这时,表示粒子能量等于动能与势能之和的公式失去了意义。即使在势垒右方发现粒子,也不存在理论上的困难。 定义传输系数(透射系数)为 (23) 对1维Schrödinger波方程求解,可计算Jtr和Jinc,从而求出T的算式,并近似地给出: (24) 令 (25) 由于U0>E,α>0;现在有 T≅Ae-αl (24a) 图2 势垒内的消失波 早在20世纪中期物理学家即对量子隧穿展开研究。首先是隧穿的动力学理论,特别是隧穿时间如何定义;其次是用怎样的物理结构来做量子隧穿实验。在前一方面,最早有L.A.MacColl[35]的“波包在势垒的传输及反射”,认为微观粒子隧穿势垒不需要时间,后来证明并不正确,但隧穿时间非常短暂。1955年E.P.Wigner[36]讨论了相时间(phase time)定义,根据波包峰的位置进行分析,断定隧穿时间非常小,故粒子穿过势垒的速度可以比光快。他还认为隧穿时间将达到最大值,并在垒厚加大时保持恒定。这就是说,当l加大,有效的隧穿速度也不断加大而无限制;虽然透射粒子的几率急剧降低,但仍有少数粒子的运动突破了光速极限。在后一方面,1985年笔者发表了论文“波导截止现象的量子类比”[37],最早提出用量子隧道效应理论描述传统上属于经典电磁学范畴的波导,建立了相关的几率波分析理论,指出一维量子隧道过程与截止波导中的消失波传播等效。7年后,G.Nimtz小组公布了用截止波导进行的实验,得到了群速超光速(vg=4.7c)。 图3 传输线上的来回反射 电子学家们非常熟悉传输线理论(theory of transmission line);“传输线”一词的应用有两种常见情况:①平行双导线(截止频率fc=0),是非本征值问题;②波导(fc≠0),是本征值问题。图3是情况①,长度l、传播常数γ、特性阻抗Z0的均匀传输线接在信号源(es、Zs)和负载(ZL)之间,下方的图表示了波的入射、传输、反射和透射。从表面上看这个一维波动过程较复杂,实际上只要设定传输线两端的复反射系数(ρs、ρL),就可导出如下方程: (26) 实际上,微路电路中的二端口理论(theory of two-ports)可以用来分析量子理论问题。例如用ai(i=1,2)表示入射波,bi(i=1,2)表示出射波,那么一个微波或光学元件的线性矩阵方程为 (27) 图4 势垒的等效传输线模型 式中Sij是散射矩阵,在量子光学中称为变换矩阵;上式中ai、bi、Sij均为复数。正是由于学术上互相联系和贯通,使笔者于1985年提出量子隧穿的等效电路模型(图4)。由于求解1维SE所得到的解表示几率波函数ψ(z)等于入射波与反射波的合成;对符号略作改变后可重写出统一的方程: ψ(z)=C+e-γz+C-eγz (28) 式中 γ=jh0 (29) 在矩形势垒区中(0≤z≤l),当E>U0,γ是虚数;当E ψ(z)=ψ+(z)+ψ-(z) (30) (31) 于是,我们可以画出势垒效应的等效传输线,见图4;图中γ是传输线传播常数,Z0是传输线特性阻抗,Zin是传输线输入阻抗,ρ1、ρ2为势垒两壁处的反射系数。根据传输线理论,有 (32) (33) 为使几率密度流公式与传输线上功率流公式等效,定义电流类似于[-jψ′(z)],故特性阻抗为 (34) 传播常数为 (35) 故γZ0=j;现在z=0处的输入阻抗为 (36) 如势垒厚,可忽略用ρ2代表的反射,这时Zin≌Z02,ρ1≌0。 然而,等效传输线所代表的不是平行双线而是波导——一种在频域有截止现象的波动过程。首先定义与传输线上简谐电压、电流的工作频率相似的波频率作为等效波导的工作频率: (37) 相对应的波导截止频率为 (38) 故可导出等效波导的传播常数: (39) 这是描写量子隧穿现象的色散方程。现在我们得到一个重要结论,即量子隧道效应可以和介入到信号传播路径中的截止波导相比拟;当ω>ωc,是波导传输模;当ω≤ωc,是截止模。ω≤ωc,即E (40) 而根据已知的传播常数γ和特性阻抗Z0,就可求出分布参数链路中Γ形单节电路的串联阻抗Z和并联导纳Y Z=γZ0=j=jωω-1 (41) (42) 这就证明了量子隧道效应(矩形势垒)可等效为TE波导。等效电路(单节)见图5。 图5 量子隧道效应等效为TE波导的单节电路 由公式(38)可知,等效波导的ωc取决于矩形势垒的高度;故只要改变U0即可改变γ;当U0=0,有 (43) 而在U0≠0,且U0>E时,消失态的衰减常数α与γ是一回事(γ=α),故可得 (44) 因而改变U0即可改消失态衰减常数;同时我们了解在几率波消失场情况下波函数满足以下对应关系: (45) 在传输线理论中,取射频电压为U,射频电流为I,则有功率流公式: (46) 式中K是常数,Z0是特性阻抗,*代表复数共轭值。在量子隧道效应描述中,与功率流对应的是几率密度流: (47) 二者是等效的;因此,波函数幅度的减小等效于电路模型中电功率的减小。 因此,笔者的理论贡献在于:提出用量子隧道效应理论描述传统上属于经典电磁学范畴的波导,建立了相关的几率波分析理论,指出一维量子隧道过程与截止波导中的消失波传播等效。因此很明显,遵循Schrödinger方程而运动的电子与电磁消失波传播的方法之间的类比,成为量子理论方法的一项重要内容;与粒子隧道效应相比,由众多光子组成的电磁波较易探测,可以使用截止频率以下波导状态。由于笔者在1985年到1991年的理论工作[37,38],无疑肯定了在物理实验中使用波导作为势垒的可能性。 实验上的证实发生在1992年~1997年间[9,10],在微波获得了群速超光速。另外,量子隧穿超光速实验又在1993年~1994年间在光波频段获得成功[7,8],使用的是固体介质势垒(在SiO2基片上搞多层涂复而形成的结构);文献[7]用实验证明了:光子经过势垒的速度比光速大70%(v=1.7c)。最后,2007年利用玻璃双三棱镜的间隙构成势垒,证明微波光子以超光速穿过它[39];研究人员说,这虽违反了SR,但可以用QM和QED很好地解释。 对超光速实验现象的研究给人们以重要的启示——必须把经典电磁理论与量子理论结合起来才能深刻认识有关物理现象。例如2007年G.Nimtz和A.Stahlhofen在解释其双三棱镜超光速实验时说,光学中的消失模对应QED创始人Feynman引入的虚粒子(virtual particles),而双三棱镜的受抑全内反射(FTIR)就是典型例子,即用宏观尺度的结构可以演示消失模的QM式行为。由于相移为零,通过势垒的传播几乎不需要时间。 (a) (b)图6 双三棱镜超光速实验示意 隧穿时间(traversal time of particle tunneling through a barrier)在超光速研究中占有重要地位。图6是用双三棱镜超光速实验的方法示意,使用两块玻璃棱镜,拼起来是每边40cm的立方体。使用波长较长的微波(λ≌33cm);对大隧穿距离而言λ足够长,对光子路径可被拐弯而言λ足够短。实验时使微波束从第一个三棱镜面的侧方斜向射入(θ>θc),在镜内底面被反射后由另一斜面射出,到达检测器A。根据Bose-QTE效应,有少数波束穿过底面,并通过间隙d从第二个三棱镜的底面进入该棱镜,再折射出去到达检测器B。由于A、B的位置对称安放,在d=0时两个光路的长度相同。但当d≠0,后一光路较长,增量为d。现在的实验发现两个光路的信号传输时间没有差别,或者说两路微波到达A、B的时间相同。故可判断后一情况的波速较快,或者说微波穿过间隙(势垒)没有耗费时间,即速度为无限大(即便v≠∞,也可断定v>c,而且大出很多)。对图6(a)有: (48) 式中v1、t1分别为由E到B的速度和时间,l2是Goss-Hänchen位移造成的;当拉开棱镜造成间隔d时,亦即对图6(b)而言,由E到B的速度为 (49) t2是相应的时间;如实验发现t1=t2=τ,则有: (49a) 故v2>v1;若v1是光速,则有 (49b) 故v2>c,亦即发现了超光速。此外,实验还发现当拉开棱镜(即逐步加大d)时,隧穿时间不变;但在d≥1m时就无法观测了。……考虑到J.J.Carey[40]的实验,我们可以说“从太赫波到微波都以双三棱镜实现了超光速的波传播”。 就图6而言,隧穿时间是指光(波或粒子)通过距离d所需时间。由于距离d与QM隧道效应的势垒宽度相对应,不应从经典物理和宏观尺度出发简单地看待问题。实际上,有的研究领域(如超晶格、薄膜生成、纳米技术)中的势垒宽度d非常小,因此人们需要的是与隧穿性质、隧穿输运的动力过程相应的时间特性的理解,在长期研究过程中就有了各种不同的定义和表述方式。 (50) 式中△z是粒子终点位置与起点位置之差,△Ф是SE定态解中透射波与入射波的相位差[43]。Wigner还认为粒子隧穿时的速度可能比光速快。 相时间定义获得了应用,例如1962年T.Hartman[42]对波包隧穿(tunneling of a wave-packet)作研究后认为,当势垒厚度增加以致“不透明”时,相时间达到饱和为一恒定值,厚度再增加则粒子速度会不断增大到光速以上。1983年M.Buttiker[43]用居留时间(dwell time)定义讨论一维隧穿,该定义是积分的粒子密度除以入射流通量,物理意义则表示粒子在区域内所用的平均时间。同年(1983),T.Sollner[44]等以实验证明隧穿过程的时间非常短(τ<10-13s);1987年M.Tsuchiya[45]首次实现了对隧穿时间的直接测量。……其他工作还有许多,如定义复时间(complex time)、互作用时间(interaction time)等,说明问题的复杂性。如上所述,可以知道经典电磁理论中的简单定义和论述(针对相延时和群延时)似不可直接移用于量子隧穿。 (51) 式中Ф是相位,如取Ф=βz,则有 (52) 故所谓相时间速度(phase time velocity)就是群速vg,而非通常的相速vp! 现在我们讨论负波速现象,特别是量子光学中的负群速实验。1905年Einstein[20]否定了物质作超光速运动的可能性,1907年Einstein[47]又否定了信号以超光速传送和存在负速度的可能性。但在1914年A.Sommerfeld和L.Brillouin[46]从经典理论出发进行分析并提出波速理论,对相速(vp)、群速(vg)、能速(ve)、信号速(vs)在全频域的变化规律作了阐述,指出“超光速群速”和“负群速”都可能存在。近年来的实验已充分证明了这一判断的正确性[48]。不仅如此,笔者在研究截止波导理论和消失态的过程中[38],不仅发现波的群速为负的可能,而且发现了波的相速为负的可能——这样的理论判断也为实验所证实[49]。因此,文献[47]的有关错误已被理论和实验所证明。……Sommerfeld假定在t=0时向媒质表面(z=0)输入一个正弦信号,则在时间t、深度z处的波可由一个积分方程表达: (53) 式中复频域由p=σ+jω代表,实数σ要保证积分路径在一定区域内,ω0是稳态载频。上式也写作 (54) 式中n=n(p)是复折射率。现在知道,直到t=z/c,才有波前(波阵)到达,波前速度是c;当t=z/c,稳态、瞬态分量抵消,波仍为零;这表示信号总是从零起逐步建立。当t>z/c,就有 f(z,t)=e-αzsin(ω0t-βz) (55) 式中:α、β分别为媒质的衰减常数、相位常数。在稳态完全建立之前的过程,则称为预现波(precusors),也叫前兆——它逐渐而迅速地发展,完成一个连续的过渡。 图7 关于电磁波波速的Brillouin图 对于Sommerfeld积分方程,一般讲无法求出封闭形式的解。但有求积分近似值的一种方法——把原来的积分路径变形为一条通过点ps(称为鞍点)的路径,故这个鞍点是对积分产生最大贡献的点。在求积分值时,可把注意力集中在鞍点附近,亦即群速为z/t的频率附近。图7是部分结果(vp和vg);对横坐标轴(角频率ω),必须分为两大范畴而作观察——中心频率(ω0)附近的反常色散区,以及远离反常色散区的频域(低端和高端)。图7中的实线显示了频率由0~∞的全领域中c/vg的变化。我们看到,在中心频率ω0附近,c/vg可为零(这表示vg=∞),然后转变为负值(这表示vg<0)。正是这条曲线表明负群速比无限大群速更进了一步,或者说前者达到了比后者更快的速度。为准确起见,我们引述L.Brillouin的著作中的一段话(用英文原文)如下:“It is then easy to construct graphically the curve forc/vg.This curve presents a curious anomaly in the absorption band.c/vgcan become less than 1,and even less than zero.This means that the group velocityvgcan be greater than the velocity of light c,can be infinite and even negative!”因此,早在1960年Brillouin即指出群速可以比光速大,可以是无限大,甚至可以为负值。 但必须指出,Brillouin波速理论中未有负相速,图7中的虚线表示c/vp与频率的关系,由该曲线可知c/vp可大于1或小于1,亦即vp 应当注意的是,Sommerfeld、Einstein、Brillouin三位都是经典物理时代的科学家,与量子时代是脱节的。1960年发明的激光,他们或因去世而不知晓,或因年老而不甚理解;仅此一例即说明这些曾作出贡献的科学家已与量子时代格格不入。然而正是量子光学(Quantum Optics,QO)吸引了大批较年轻的科学家进行研究,并做出了出色的实验(包括负波速实验)。由下述例子可看出量子光学(QO)实验与经典物理实验的重大区别。 (a) (b)图8 WKD实验的铯原子能级图和结果示意 2000年发表的王力军实验也称为WKD实验[11],受试物质为铯(Cs)原子气体,它不是自然存在的。天然的铯有16种可能的量子态,称为超精细基态磁副能级。把所有的铯原子激励到其中一种量子态,它几乎与绝对零度的温度相对应。这是靠激光器的光泵作用达到的,而激光也不是自然界具有的现象。图8(a)是增益辅助反常色散过程的原子能级图。原子在气态时,每个原子可有3种状况:激发态|0〉、|1〉和|2〉。首先由光泵作用制备出所有原子的基态。采用两束强连续波Raman光束E1、E2,使其通过原子媒质传播。E1、E2的频率为f1、f2,频差为小量2△;两种场的调谐通过原子跃迁频率f01实现(体现为较大的△0)。由于E1、E2辅助场的Rabi频率小于△0,大多数原子保持在|1〉态。现在引入探束Ep,会发生Raman跃迁,原子在吸收来自E1和E2场的Raman激励光子时会发射光子到Ep场,并造成由|1〉到|2〉的跃迁。由于探束场内有两种增益频率作用,增益值最大,探束场与跃迁场(E1或E2)发生谐振时均会引起最大增益作用。简言之,在两个增益线之间会出现反常色散区。实验布置的核心是一个铯蒸气室,长6cm,用Pyrex玻璃制成,内壁敷石蜡,以维持铯原子基态自旋极化。气室放在小而均匀的磁场中(1Gs),场方向与光传播方向平行。外加磁场的诱导和外加2个激光束的pump作用,使容器内的铯气达到所需的物理状态。这个人为地使光脉冲以超光速运动的实验是量子光学的,也是出色的,详细情况见[11] 和[50]。图8(b)是实验结果示意,G曲线表示增益与频率的关系,n曲线表示折射率与频率的关系;由于是示意图,纵坐标未给出刻度数据。 现在可以看出,图8是量子光学(QO)以及经典物理概念的代表,而实验是两方面结合的结果;因为折射率(refraction index)和反常色散(anomalous dispersion)都是经典概念(图8(b)中a、b两点之间为反常色散区)。定义折射率为 (56) 而群速指数为 (57) 根据Rayleigh公式,有 引入二项式定理(取近似),并作进一步运算后得 (58) 故群速公式成为 (59) 在正常色散时dn/df>0,总有vg (60) 如n>0,那么在反常色散足够强时式(60)才能满足。如果反常色散进一步加强,达到n+fdn/df=0,速群vg成为无限大(vg=∞)。那么,实现负速群的条件是什么呢?假如满足以下两个条件 (61) (62) 这时有vg<0,实现了负群速;WKD实验就属于这种情况。 论文作者说:“我们测量到群速指数ng=-310±5,实际上,这意味着通过原子气室传播的光脉冲到达出口处要比它在真空中走过同样距离的情况早许多,即脉冲峰在进入气室之前就已离开了气室(peak of the pulse appears to leave the cell before entering it)”。因此WKD实验的结果是vg=-c/310。在国内,有人说“这是亚光速,因为|vg|=c/310,故|vg| (a) (b) (c)图9 四波混频实验方法的说明 2012年5月初西北工业大学杨新铁教授发来邮件,说“最近美国科学家研发出超光速脉冲”;这个新消息在Google上和百度上也是刚出现,是指美国标准与技术研究院(NIST)提出的一种新方法,称为四波混频(four-wave mixing)。笔者在检索后得知领头的科学家是P.D.Lett博士,而他在2007年即发表过有关论文;现在的报道是指R.T.Glasser等[12]的论文“Stimulated generation of superluminal light pulses via four-wave mixing”,其中的超光速是指群速超光速,更具体些讲是负群速。大致意思是说,研究人员向充有铷(Rb)原子蒸气的小室发送长200ns的种子激光脉冲,小室放大了它并将峰值前移,使脉冲波峰比真空中光速c快了50ns。所谓四波混频是指向媒质注入弱光束并另行注入一个不同频率的泵浦光束,如图9。通过这个过程产生出第三种频率的光束,因为泵浦光束中的光子转换成注入光束中的光子产生了共轭模式。由于四波混频色散,放大了的种子脉冲具有负群速,并且激励产生传播速度更快的共轭脉冲。这种反常色散是由于在种子脉冲频率和产生的共轭脉冲频率处的不对称增益线和吸收线造成的。总起来讲这是由热的铷蒸气中通过four-wave mixing 而成功造成群速超光速的光脉冲。作者指出不仅注入脉冲以负群速传播,而且在分隔空间模式通过四波混频产生不同频率的另一个脉冲,并且其速度比参考脉冲在真空中的传播速度快。由于在分隔空间模式中产生一个共轭脉冲,除了种子脉冲以外,这个共轭脉冲也可能以超光速传播。四波混频的过程是消灭两个泵浦光子并且产生单一的探测和共轭光子。 实验技术情况如下:①泵激光为线极化的连续波,功率大(约220mw),波长λ=795nm;②输入种子脉冲为垂直极化,峰功率约5μw,半高宽200ns;③小室长1.7cm,內部原子蒸气温度约116℃;④群速度是通过测量脉冲峰值相对于光速c传播的参考脉冲的到达时间来确定;⑤当泵浦光束很强时,注入的种子脉冲和产生的共轭脉冲都可能表现出负群速,并且取决于注入的泵浦脉冲和种子脉冲失谐。 我们知道,量子光学(QO)是以量子理论或激光技术研究光学问题的学科。以上举出的两个例子(WKD实验和Glasser实验)是QO实验的典型例子,其实施方法是经典物理实验所不具备和做不到的。这两个例子也证明,量子超光速性(QS)研究已成为QO的一个分支。我们认为在国内重复这些实验有难度,而且Lett-Glasser实验比WKD实验更难。我们还注意到西方国家的这类论文一般不提SR,只是说自己工作的意义是可能在光通信、量子纠缠、量子信息学研究等方面。表1给出多年来关于负波速的一些有代表性的理论与实验工作。 表1 多年来关于负波速的部分研究工作 续表 荷兰物理学家Hendrik Casimir于1948年提出存在一种力,现在的通俗解释为:当计算两个互相平行的不带电导体板之间的能量时,当板距d小于真空中虚光子的波长,长波排除,板外的无限多模式大于板内的无限多模式,造成一个小的力量使两板靠近。计算Casimir力有许多方法,例如可用Green函数描写Casimir能,就可以计算与边界条件对应的4种情况。从量子场论(QFT)出发而进行思考,可以认为真空中放置双板后改变了真空的结构,故有两种真空:板外的常态真空或自由真空,板间的负能真空。1990年的研究证明,对于与板垂直的电磁波传播而言,真空中的光速并不相同,变化量△c/c约为1.6×10-60d-4,故当d=10-9m时,△c=10-24c。因此,由于量子电动力学双环效应,K.Scharnhorst断定这会使电磁波的相速和群速大于真空中光速c。虽然超光速的量很小,但却提升了对原理的兴趣。可以说,在发现Casimir效应许多年后的今天,它仍使人们感到惊奇。 Casimir效应是一种宏观量子现象,是从量子场论出发而演绎出来的。可以认为Casimir能是负能,两导体板间的Casimir力是互相吸引。“负能量”可理解为“板间的虚空比真空还空”,必定产生内向力使板子靠近。既然Casimir效应已被实验所证明[60,61],我们就得承认上述“两种真空”的说法是正确的。既如此,“板内和板外的光速可能不一样”就是合乎逻辑的了。因此,正是边界条件的改变影响了真空,从而影响了电磁波的传播速度。换言之,光的传播是取决于真空的结构,而“真空有结构”正是量子物理学的基本观点。 Casimir效应型结构(双平行板)是把边界条件强加到光子真空涨落上,这时可用量子电动力学(QED)来考虑问题。1990年K.Scharnhorst[62]对此作了双环修正(two-loop corrections)计算,根据QED有效作用发现,对于处在真空中的双板,考虑与板垂直的光传播时,光速会发生改变。Scharnhorst发现这种“改变”是光速增大了(进入超光速区)。图10是作QED计算时的双环图(two-loop diagram),它对光子极化算子(photon polarization operator)作出贡献,因而对折射率的计算作出贡献。 图10 QED计算中的双环图 总之,Scharnhorst并未计算“光子在两块金属板之间的飞行速度”,而是计算双板间波垂直传播时的波速,发现相速比光速略大(vp>c)。在频率不高条件下讨论,可以忽略色散,群速等于相速,故群速比光速大(vg>c)。1993年G.Barton和K.Scharnhorst[63]称两块金属平板为“平行双反射镜”(parallel mirrors),重新解释有关问题,指出:“由于量子化场的散射,在两个平行双反射镜之间垂直穿行的频率为ω的光,所经历的真空是折射率为n(ω)的色散媒质。我们早先的低频结果表示n(0)<1,是结合了Kramers-Kroning色散关系和经典的Sommerfeld-Brillouin论据,以宣示两者之中任一情况:①n(∞)<1,因而信号速度c/n(∞) >c;②n的虚部为负,反射镜间的真空不足以像一种正常无源媒质那样对光探测作出响应。”因此很明显,两作者关注的是真空的性质;他们认为在Casimir效应的物理情况和条件下,真空的折射率不再等于1,而比1要小。当然这仍是QFT的观点,与经典物理学不同。……图11是笔者根据情况的发展提出的学科关系,实线表示“有密切联系”,虚线表示“有联系”。可以说,Casimir效应与超光速研究有关并不令人特别奇怪。 大家知道,李政道教授曾一再提醒物理学界“要研究真空的构造(construction of vacuum)”,甚至创造新的物理真空。这一点其实在Casimir效应研究中已有了充分的体现;而正是新真空的存在造成了超光速现象。这是非常生动而奇妙的研究领域。 图11 Casimir效应与各学科的关系 量子力学(QM)从提出至今已有86年历史。现在,它已成为现代物理学的基础与核心,其影响还在不断地扩展。一系列的相关实验,诸如关于Bell不等式的判别实验,关于量子隧穿呈现出来的超光速性实验,以及近年来关于量子纠缠态的实验,使用量子光学(QO)和激光高科技进行的负群速实验,还有对Casimir效应中蕴含的群速超光速计算,等等;均已超越了哲学思辨式的探讨,显示出一系列全新的非经典物理现象,引起了人们的极大关注。近年来,不仅有众多科学工作者在从事QM基础理论与量子信息学(QIT)理论与实验的研究,有关新著作也在不断出版;这是非常可喜的现象。 与此同时,也引发出一些争论,甚至是激烈的争论,这本属正常。但是,有的文章却在缺乏事实依据的情况下企图否定QM这一理论体系,至今不承认QM这个伟大理论的成就,亦不承认QM非局域性为超光速提供了现实的可能性。这是一种“复古”的倾向,在物理概念上也制造了一些混乱。有人企图用SR反对乃至批判QM,这种“原教旨主义”式的做法是可笑的。因为正如英国科学刊物New Scientist所说:“相对论仍然是一种古典理论”;与此相对照,QM和QO则具备现代科学理论的特征,尽管它描写的量子世界与人类生活经验常常大相径庭。又如Sommerfeld-Brillouin波速理论今天仍有价值,但其中一些论断与现在的许多实验并不相符。因此,“要与时俱进”才是正确的口号,即使对大师级人物也应扬弃他们的那些过时的和错误的东西。 1977~1991年间,笔者通过截止波导理论研究发现了负波速(负相速、负群速)现象,此发现写在了有关著作中,并于1999~2000年间由国外的实验所证实。我们在1985年从量子理论出发分析波导这种宏观器件取得了成果,建立了QM隧道效应的等效传输线电路模型,发展了消失态理论;这些工作也在国外的实验中得到了验证。此外,笔者与人合作在无线电波频率上进行了模拟光子晶体的同轴系统的实验,获得了群速超光速的实验结果。另外,笔者领导建立了以三棱镜为基础的微波实验系统,两镜间隙即构成量子势垒。……这些初步的理论与实验工作是我们通过持续努力所作的贡献。必须指出,笔者于2005年提出广义信息速度(GIV)、2010年提出量子超光速性(QS)这两个概念和术语,为相关研究指明了方向,也是本文的基础。而本文内容则证明了量子世界的非局域性和超光速性是客观存在的事实,也展示了大自然的无比深邃和丰富。 必须说明,虽然量子理论揭示了超光速的可能性,近年来又出现了多个著名的实验,以及多方面的工作;但其本身并不直接回答“物质、能量和信息能否以超光速传送”的问题。例如人类在未来是否可能设计和建造超光速宇宙飞船飞往其他星系?量子理论不能给出答复。又如在信息传送方面,一些物理学家虽然承认“纠缠态违背了相对论”,承认“在两个互相纠缠的粒子之间有某种东西的传播速度超过了光速”,但却仍然认为目前还不能利用纠缠态实现超光速信息传送。总之,在现阶段科学尚不能回答的问题还很多,它的历史还短;其发展还需要时间。 尽管如此,我们却不应气馁,亦不能停止努力和追求。例如,对量子超光速性的研究促使笔者于2010年提出如下的实验建议[64]:对现有的高能物理实验设备(粒子加速器)进行改造,寻找可能存在的以超光速运动的奇异电子(strange electron)。提出这个设想有以下几个理论前提和基础:①不认为以光速运行的粒子的质量会成为无限大;②认为量子势垒可以使粒子加速(quantum tunneling现象);③虽知全世界的加速器都是亚光速类型的系统(用电磁场使带电粒子加速),也不认为超光速实验无路可走,而建议利用电磁相互作用来实现超光速;④认为既然科学界还未找到加速中子的技术,受试粒子仍用荷电粒子(最方便的是电子),这些想法请专家们指教! 笔者之所以提出上述实验建议是基于这样的事实:目前全世界做超光速研究的科学家尚无人以实验证明“有质量的物质粒子(如电子、质子、中子,或是原子、分子),能够以超光速飞行”,因此,虽然航天专家询问“在未来设计和建造光速飞船或超光速飞船的可能性究竟如何”,但笔者始终认为作为科学家还是要从最基本的实验做起,然后才能尝试回答上述问题。因此必须强调“超光速研究目前还处在非常初级的阶段”,未来会怎样尚无法预测。 * * * 致谢:在思考本文内容的漫长时间中,笔者曾多次与量子力学专家、首都师范大学物理系耿天明教授交流讨论,获得有益的启发,谨此致谢! [1]Schrödinger E.Quantisation as a problem of proper values[J].Ann d Phys,1926,79(4),80(4),81(4). [2]Einstein A,Podolsky B,Rosen N.Can quantum mechanical description of physical reality be considered complete[J].Phys Rev,1935,47:777-780. [3]Aspect A,Grangier P,Roger G.Experiment realization of Einstein-Podolsky-Rosen-Bohm gedanken experiment,a new violation of Bell’s inequalities[J].Phys Rev Lett,1982,49:91-96. [4]Bell J.On the problem of hidden variables in quantum mechanics[J].Rev Mod Phys,1965,38:447-452. [5]Brown J,Davies P(易必洁译).原子中的幽灵[M].长沙:湖南科技出版社,1992. [6]Enders A,Nimtz G.On superluminal barrier traversal[J].J Phys France,1992,(2):1693-1698. [7]Steinberg A M,Kwait P G,Chaio R Y. Measurement of the single photon tunneling time[J]. Phys Rev Lett,1993,71(5) :708-711. [8]Spielmann Ch,et al.Tunneling of optical pulses through photonic band gaps[J].Phys Rev Lett,1994,73(17) :2308-2311. [9]Haibel A,Nimtz G.Universal relationship of time and frequency in photonic tunneling[J]. Ann d Phys,2001,10:707-712. [10]黄志洵.论消失态[J].中国传媒大学学报(自然科学版),2008,15(3):1-9. [11]Wang L J,Kuzmich A,Dogariu A.Gain-asisted superluminal light propagation[J]. Nature,2000,406:277-279. [12]Glasser R T,et al.Stimulated generation of superluminal light pulses via four-wave mixing[J].arXiv:1204.0810 vl [quant ph],2012. (also:Phys Rev Lett 2012,108(17,26)) [13]Gisin N,et.al.Optical test of quantum non-locality:from EPR-Bell tests towards experiments with moving observers[J].Ann Phys,2000,9:831-841. (又见:Salart D,et al. Testing the speed of “spooky” action at a distance[J]. Nature,2008,454:861-864.) [14]黄志洵.论Casimir效应中的超光速现象[J].中国传媒大学学报(自然科学版),2012,19(2):1-8. [15]黄志洵.超光速实验的一个新方案[J].前沿科学,2010,4(3):41-62. [16]黄志洵,耿天明.超光速研究中的几个理论问题[J].中国工程科学,2007,9(4):6-17 [17]Lorentz H A.Electromagnetic phenomana in a system moving with any velocity less than that of light[J].Konin Akad Weten(Amsterdan),1904,6:809-831. [18]Klenberger R,et al.Atomic transient recorde[J].Nature,2004,427(6977):817-831. [19]Levine I N(宁世光,等译).量子化学 Quantum Chemistry[M]. 北京:人民教育出版社,1980. [20]Einstein A.Zur elektrodynamik bewegter Korper[J].Ann d Phys,1905,17(7):891-895. [21]Einstein A(郝建纲,刘道军译).相对论的意义[M].上海:上海科技教育出版社,2001. [22]Segre E(夏孝勇等译).从X射线到夸克[M].上海:上海科学技术文献出版社,1984. [23]Born M,Einstein A.The Born-Einstein Letters(1916-1955)[M].Palgrave Macmillan,2005. (中译本:范岱年译,玻恩—爱因斯坦书信集[M].上海:上海科技教育出版社,2010.) [24]Bohr N.量子力学和物理实在[A]戈革译.尼耳斯·玻尔集(第7卷) [C].北京:科学出版社,1988. [25]Bohr N.物理实在的量子力学描述能不能被认为是完备的?[A]戈革译.尼耳斯·玻尔集(第七卷)[C].北京:科学出版社,1998. [26]Bohm D.Quantum Theory[M].London:Constable and Co,1954. [27]Huang Z X(黄志洵).Some problems in research of EPR thinking[A].超光速研究的理论与实验[C].北京:科学出版社,2005. [28]潘建伟,塞林格.量子态远程传送的实验实现[J].物理,1999,28(10):609-613.(又见:Bouwmeester D.Experimental quantum teleportation[J].Nature,1997,390:575-579.) [29]Eberhard P H.Quantum theory and pictures of reality[M].Berlin:Springer,1989. [30]Feinberg G.Possibility of faster-than-light particles[J].Phys Rev,1967,159:1089-1105. [31]Bohm D.A Suggested interpretation of the quantum theory in terms of hidden variables[J].Phys Rev,1952,85:180-193. [32]Franson J D.Bell inequality for position and time[J].Phys Rev Lett,1989,62:2205-2208. [33]曹庄琪.导波光学[M].北京:科学出版社,2007. [34]黄志洵.超光速研究的量子力学基础[J].中国工程科学,2004,6(4):15-25. [35]Maccoll L A.Note on the transmission and reflection of wave packets by potential barriers[J].Phys Rev,1932,40:621-626. [36]Wigner E P.Lower limit for the energy derivative of the scattering phase shift[J]. Phys Rev,1955,98:145-147. [37]黄志洵.波导截止现象的量子类比[J].电子科学学刊,1985,7(3):232-237. [38]黄志洵.截止波导理论导论[M].北京:中国计量出版社,1981. [39]Anderson M.Light seems to defy its own speed limit[J].New Scientist,2007,(10). [40]Carey J J.Noncausal time response in frustrated total internal reflection[J].Phys Rev Lett,2000,84,1431-1434. [41]顾本源.量子力学中电子隧穿势垒的时间[J].北京石油化工学院学报,2002,10(4):64-67. [42]Hartman T E.Tunneling of a wave packet[J]. J Appl Phys,1962,33:3427-3433. [43]Buttiker M.Larmor precession and the traversal time for tunneling[J].Phys Rev,1983,B27:6178-6188. [44]Sollner T C,et al.Resonant tunneling through quantum wells at frequencies up to 2.5 THz[J].Appl Phys Lett,1983,43:588-590. [45]Tsuchiya M,Matsusue T,Sakaki H.Tunneling escape rate of electrons from quantum well in double-barrier heterostructures[J].Phys Rev Lett.1987,59:2356-2359. [46]Sommerfeld A.Uber die fortpflanzung des lichtes in dispergierenden medien[J].Ann d Phys,1914,44(1):177-182.(又见:Brillouin L.Uber die fortpflanzung des lichtes in dispergierenden medien.Ann d Phys,1914,44(1):203-208.also:Brillouin L.Wave propagation and group velocity[M].New York:Academic Press,1960.) [47]Einstein A.The relativity principle and it’s conclusion[J].Jahr der Radioaktivität und Elektronik,1907,4:411-462. (中译本:关于相对性原理和由此得出的结论[A].范岱年,赵中立,许良英译.爱因斯坦文集,第2卷[C].北京:商务印书馆,1983.) [48]黄志洵.论电磁波传播中的负速度[J].中国传媒大学学报(自然科学版),2007,14(1):1-11. [49]Wynne K,et al.Tunneling of single cycle terahertz pulse through waveguides[J].Optics communication,2000,176:429-435. [50]黄志洵.超光速研究新进展[M].北京:国防工业出版社,2002. [51]Garrett C G B,McCumber D E.Propagation of a Gaussian light pulse through an anomalous dispersion medium[J].Phys Rev A,1970,1(2) :305-313. [52]Chu S,Wong S.Linear pulse propagation in an absorbing medium[J].Phys Rev Lett,1982,48(11) :738-741. [53]Mitchell M W,Chiao R Y.Causality and negative group delays in a simple bandpass amplifier[J].Am Jour Phys,1998,66:14-19. [54]Wynne K,Jaroszynski D A.Superluminal terahertz pulses[J].Optics Letters,1999,24(1),25-27. [55]Munday J N,Robertson W M.Negative group velocity pulse tunneling through a coaxial photonic crystal[J].App Phys Lett,2002,81(11) :2127-2129. [56]Akulshin A M,Cimmino A,Opat G I.Nagative group velocity of a light pulse in cesium vapor[J].Quant Electr.,2002,32:567-569. [57]陈徐宗等.光脉冲在电磁感应介质中的超慢群速与负群速传播实验研究[J].北京广播学院学报(自然科学版),2004,11:19-26. [58]Stenner M D,Gauthier D J,Neifeld M A.The speed of information in a fast-light optical medium[J].Nature,2003,425:695-698. [59]Casimir H.On the attraction between two perfect conducting plates[J].Proc Ned Akad Wet,1948,51:793-797. [60]Lamoreaux S K.Demonstration of the Casimir force in the 0.6 to 6μm range[J].Phys Rev Lett,1997,78,5-8. [61]Mohideen U,Roy A.Precision measurement of the Casimir force from 0.1 to 0.9μm [J]. Phys Rev Lett,1998,81:4549-4552. [62]Scharnhorst K.On propagation of light in the vacuum between plates[J].Phys Lett B,1990,236(3) :354-359. [63]Barton G,Scharnhorst K.QED between parallel mirrors:light signals faster than light,or amplified by the vacuum[J].J Phys A:Math Gen,1993,26:2037-2046. [64]黄志洵.超光速实验的一个新方案[J].前沿科学,2010,4(3):41-62. [65]Gehring G M,et.al.Observation of backward pulse propagation thhough a medium with a negative group velocity[J]. Science,2006,312:895~897. (责任编辑:龙学锋) DiscussionsoftheQuantumSuperluminality HUANG Zhi-xun (Communication University of China,Beijing 100096) A.Einstein held an opposite attitude towards Quantum Mechanics(QM),which first appeared in 1926 and reached the top in 1935 when he,together with B.Podolsky,N.Rosen published the EPR thesis and it promotes science development in an opposite side.The EPR thesis is based on Special Relativity(SR).Both SR and EPR deny the possibility of faster-than-light.But QM allows the existence of faster-than-light,agreeing to non-locality of QM is the premise of researching in faster-than-light.In 1965,during the interview John Bell confided that his unequality was the outcome of EPR thinking,which denied ultra-space effect under EPR thesis,conditions resulted in quite peculiar correlations that QM predicted.The results of Aspect’s experiments were within expectation that QM has never been wrong now and will not in the future despite of strict requirements.Undoubtedly,the experiments proved that Einstein’s ideas didn’t hold water.In Bell’s opinion,to get rid of the difficulties after the announcement of the Aspect’s experiments,it intends to go back to Lorentz and Poincarè,and assume that ether existed as a referential system in which matters went faster than light.Bell repeatedly pointed out that be wanted to go back to ether because EPR had predicted there was something faster than light in the background.…… Since 1992,it is reported that there have been many successful faster than light experiments.Some of them are based on quantum tunneling effect;some are based on classic physical phenomena such as evanescent waves,anomalous dispersion.And in 2008,D.Salart et.al.performed a experiment using entangled photons between two villages separated by 18km.In conclusion,the speed of the influence of quantum entanglement would have to exceed than of light by at least four orders of magnitude,i.e.104c~107c.Anyway,this experiment was the summation of discussions about the EPR thesis for a long time. For the past 25 years Quantum Superluminality was one subject of my chief study.In 1985,we proposed the model of quantum potential barrier equivalent circuit.In 1991,we first indicated that there could be the wave velocityvp<0andvg<0 in the evanescent waves mode of the waveguide below cut off and the book “An Introduction to the Theory of waveguide Below Cut-off ” made me get the First National Scientific and Technology Book Award of China.Moreover,in 2003 we through an experiment in the coaxial photonic crystal,a superluminal group velocity of (1.5~2.4)c are observed in the stop-band of frequency.In 2005,we suggested the term of General Information Velocity(GIV);and in 2010,we suggested the term of Quantum Superluminality(QS),and also suggested remodel the existing accelerator to discover the superluminal strange electron.Now,this paper discusses some problems of Quantum Superluminality profoundly,such as the velocity definition of the microscopic particles,the relation between the EPR thinking and the faster-than-light research,the interaction speed of the quantum entangle-state,superluminality of the quantum tunneling,the negative wave velocity,QS of the Casimir effect.We show that the unite of Quantum Optics(QO)and classical physical sujects are becoming more important. Since 2000,the negative group velocity experiments are always employing some atomic metal(such as Cs、Ka、Rb) vapor for tests.It make full use of the latest achievement in laser science and technology,then it was modern physical experiment in QO,not the classical physical experiment.The negative group velocity not only the special situation of faster-than-light,but also has the features:the exiting pulse’s peak can appear to exit the medium before the peak of the input pulse enters.So it was different that of classical causality. Although that knowledges and discovers of QS are widen and lively,then it greatly inspired us;but it is not the immediate conclusion that answers some questions about the possibility of material,energy and information according to faster-than-light propagation.To design the ingenious and convincing superluminal experiments are also basic task of scientists. quantum mechanics(QM);quantum superluminality(QS);quantum entanglement state(QES);quantum tunneling;negative wave velocity;quantum optics(QO) 2012-05-07 黄志洵(1936-),男(汉族),北京市人;中国传媒大学教授、博士生导师,中国科学院电子学研究所客座研究员。 O412 A 1673-4793(2012)04-0001-17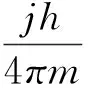








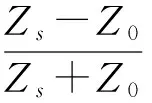
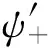














7 量子隧穿时间与负波速

























8 Casimir效应中的量子超光速性[59,14]


9 结束语

