一道课本习题的探索性学习与类比
● (孝感高级中学 湖北孝感 432000)
一道课本习题的探索性学习与类比
●王国涛(孝感高级中学 湖北孝感 432000)
探索性学习是培养学生能力的有效途径之一.笔者从一道课本习题(普通高中课程标准实验教科书《数学》必修4第144页第5题)出发,引导学生在课堂上积极探索、突破和创新,课后忘我参与,兴趣盎然,惊喜地得到了2个实用而优美的结论,教学取得了良好的效果.
1 原题呈现
原题设f(α)=sinxα+cosxα,x∈{n|n=2k,k∈N+},利用三角变换,估计f(α)在x=2,4,6时的取值情况,进而对x取一般值时f(α)的取值范围作出一个猜想.




(1)
倘若仅满足把答案猜想出来,则无异于“入宝山而空返”,学生也意犹未尽.那么,猜想是否正确,该怎样证明呢?笔者在课堂上让学生自己探索证明思路和方法.
2 猜想的多角度证明
生1:既然是2k次方,可以考虑用二项式定理将其展开,但不能合并,用二倍角公式即可.
证法1利用二倍角公式和二项式定理证明
因为

又-1≤cos2α≤1,所以0≤cos22α≤1.由不等式和组合数的性质得
因此

生2:我是从函数角度考虑的,通过同角关系式构造幂函数,再利用导数知识证明.
证法2构造函数,利用导数知识证明
令x=sin2α,0≤x≤1,则
f(α)=sin2kα+cos2kα=g(x)=xk+(1-x)k.
当k=1时,g(x)=1,式(1)成立.当k≥2,k∈N+时,由
g′(x)=kxk-1-k(1-x)k-1=k[xk-1-(1-x)k-1]=0,


又因为g(0)=g(1)=1,所以

生3:我考虑到要证明的结论与正整数有关,故可以利用数学归纳法证明.
证法3利用数学归纳法证明
当n=1时,sin2α+cos2α=1,即式(1)成立;

假设n=k和n=k+1时,式(1)成立,即

则当n=k+2时,注意到
一方面

另一方面

故

即当n=k+2时,式(1)也成立.
师:还有没有其他证明方法呢?能否从凸函数的性质考虑呢?
生4:哦!我明白了,可以利用不等式的性质和下凸函数的性质证明.
证法4利用不等式的性质和凸函数的性质证明


3 类比探究
f(α)=sinxα+cosxα(x∈{n|n=2k,k∈N+})的取值范围已经得到完美解决,那么sinmα,cosnα的差、商、积与倒数和的最值情况怎样?此时下课铃响了,此问题留给学生课后思考.学生们兴致都很高,第2天便将成果展示给笔者,其中2个优美的结论如下:

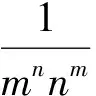



证明
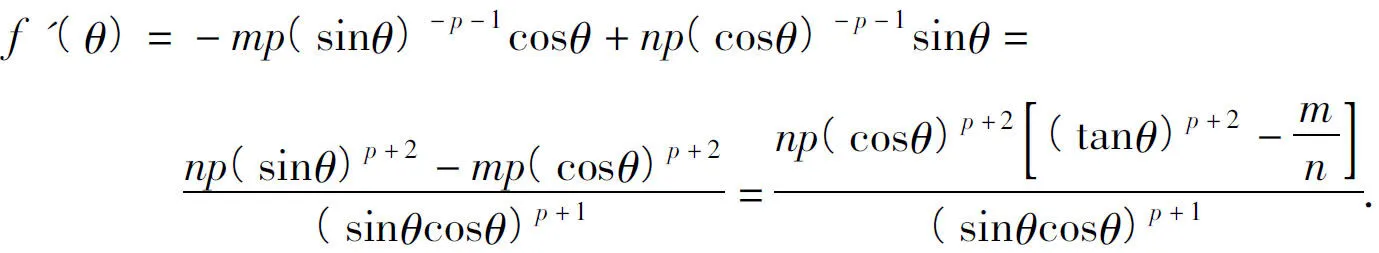


因此
4 结论应用

(2012年《数学通讯》问题99)


(2010年联盟杯高中数学竞赛预赛试题)

5 延伸思考
通过本例的证明与拓展,学生掌握了相关的知识与技能,体会到知识的联系与综合.这说明只要我们重视教材的使用,在处理教材问题时不浅尝辄止,注意引导学生吃透课本典型问题的内涵,挖掘这些问题的潜在价值,并鼓励学生对它们进行力所能及的类比,就可以让学生学得更轻松、更主动,并使他们在创造性思维方面得到发展的同时,体会到学习数学的乐趣.课本上的不少例题、习题背景丰富深刻,解题思想耐人寻味,是最好的探究素材.若教师能有意识地去引导学生进行探究和挖掘,则往往会得到一些有价值的结论和重要的解题思想,同时对激发学生的探究兴趣、培养学生的创新能力和理性思维大有裨益.

