“对勾函数”应用的思想性赏析
● (苏苑高级中学 江苏苏州 215128) ● (格致中学 上海 200001)
“对勾函数”应用的思想性赏析
●张国棣(苏苑高级中学 江苏苏州 215128) ●茹双林(格致中学 上海 200001)


表1 对勾函数的常见性质
这个函数在高考和竞赛中都有出现,能简捷地处理有关函数的单调性、值域以及不等式、方程等综合问题,蕴含了很强的思想性,现举几例,供大家欣赏!
1 数形结合,沟通抽象与形象的桥梁
数形结合,是中学阶段非常重要的数学思想,它将抽象的问题直观化、生动化,也能从表象的视觉中提炼出深刻的数学问题,用之于无形之中.

( )

(2008年江西省数学高考理科试题)


2 分类讨论,单极世界逐次突破
分类思想是根据数学本质属性的特性,将研究对象分为不同种类的一种数学思想.对勾函数蕴含了很强的分类思想,如:x,a,b的正负,这些可能都是分类之源,对思维的周密性、条理性要求较高.




(2006年上海市数学高考理科试题)
解(1)根据条件,当x=2b-1时,








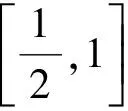

3 等价转化,实现问题的有效迁移
通过转化建立起不同知识、方法之间的转换,这种转化不仅能有效处理问题,还能化腐朽为神奇.

(2008年天津市数学高考理科试题)


4 函数与方程,知识交融的典范
函数、方程与不等式是数学的“三胞胎”,通过函数与方程的互化、交融,能将问题有效的转化、整合,形成思维的有效迁移.
例4若关于x的方程4x+(a+3)2x+5=0至少有一个实根在区间[1,2]内,则实数a的取值范围是________.
(2005年上海市高中数学竞赛试题)

简析分离变量是此类题的常见处理方法,将方程转化为函数,显现的是函数与方程思想,需心领神会.
5 换元思想,显现问题的本质结果
换元是处理复杂问题时理清思路、简化运算的有效手段,可以把分散的条件联系起来,把陌生的条件变为熟悉,显现条件与结论的联系,将隐含的问题本质结构显露出来.

(2009年全国数学高考理科试题)

简析这些三角函数问题,通过换元能显现问题的本质结构——对勾函数,换元思想就显得尤为重要了.
6 化归思想,建立起问题间结构的统一
美国加州大学的舍费尔德做过这样的“实验”:他列举了32个数学问题,要求一些专业数学工作者对它们进行分类,结果发现:
(1)各人所给出的结果是十分接近的.这种“统一性”表明对数学问题进行归类的“客观性”,即问题本身存在结构,数学家们由于有较强的洞察力而发现“十分接近”.
(2)数学家们在对问题进行分类时,除对数学内容作分析外,关于解题的基本思想,或者说基本的思维模式的考虑也占据了十分重要的地位.这种方法论方面的考虑表明:对数学问题的求解实质上是对问题结构的一种认识或揭示.
换句话说,解题就像采蘑菇,通过一个问题发现一堆问题,不同问题又有共同的根,这种化归意识需要不断给学生强化建立.




事实上,在探究“归根”的过程中,教师向学生展示数学思考问题的方式,逐步渗透方法论思想,提高数学思维的理性,使数学思维更加严谨,这既是学生建立良好数学认知结构的需要,也是提高学生数学能力和对数学整体认识水平的需要.
7 整体思想,大处着眼小处入手
根据波利亚解题研究,比较综合的问题一般都能分解成若干个基本的小问题.对问题首先要有宏观上的整体思考,洞察题目中的整体与局部的关系,从大处着眼从小处入手,这是处理复杂问题的基本策略.

(1)求f(x)的解析式;
(2)证明:函数y=f(x)的图像是一个中心对称图形,并求其对称中心;
(3)证明:曲线y=f(x)上任一点处的切线与直线x=1、直线y=x所围成三角形的面积为定值,并求出此定值.
(2008年海南省数学高考理科试题)







总之,了解一些特殊函数的性质,掌握一类问题的处理方式,提炼解题思想——长期积淀知识变得的厚重,思维就会如山般愈发沉稳.

