这么好的解法学生怎么就想不到

● (杨集高级中学 江苏灌云 222221)

这么好的解法学生怎么就想不到

●李昌(杨集高级中学 江苏灌云 222221)

高考试题对高中教学具有良好的导向作用，是教师进行教学和研究的不竭资源．高考题的利用应尽可能地对教学内容、教学方法、教学理念等进行一次“整容”，以延续和发展高考的导向价值[1].2011年江苏省数学高考试题的答案公布之后,针对其中第18题的第(3)小题，笔者发现学生的解法和思路与参考答案中的解法1基本相同,他们都感到这种解法运算繁、耗时多、易出错,甚至无功而返；对于解法2,鲜有学生能够想到,他们都不约而同地发出感叹“此解法巧妙,我怎么就想不到”.作为一线教师,在为学生感到惋惜的同时,更多的是对教学的深层次思考．

1 试题及解法

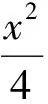
图1

解法2设P(x1,y1),B(x2,y2),则

x1>0,x2>0,x1≠x2,A(-x1,-y1),C(x1,0).

设直线PB,AB的斜率分别为k1,k2,因为点C在直线AB上,所以

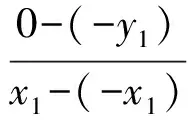
从而k1k+1=2k1k2+1=

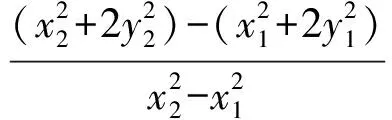
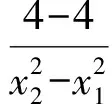
故k1k=-1,于是PA⊥PB.

2 好的解法从哪里来

一种解法产生的过程,本质上是寻找条件和结论之间的逻辑思维过程.因此,解法产生于对题目条件与结论的逻辑梳理过程之中.若条件与结论间的逻辑关系简洁明了,相应的解法自然就简单清晰.

2.1 源于对运动过程的逻辑梳理

显然,要证明2条动直线间存在垂直关系,选择动直线的斜率或者动点的坐标做为切入点是恰当的.可是,运动变化的几何元素很多,选哪个点或哪条直线呢？审视变化过程,可以发现：所有的变化都是由点P(或点A)或者直线PA的变化引起的(变化的核心元素),它们的运动带动了其他元素的变化.由于在变化过程中受椭圆方程的制约,致使直线PA与PB的垂直关系不变.因此,抓住变化的核心元素,将其作为解题的突破口,即可步步推进.

2.2 源于对运动变化中几何不变关系的代数表达

辩证唯物主义运动观告诉我们：变化是绝对的,不变是相对的.如果只看到运动,而不留心运动中存在的不变性,运动的场景便是混乱的.再次审视运动过程,以下3个几何关系始终不变：点P与点A关于坐标原点对称，点C是点P在x轴上的射影、点A,C,B共线.这3个不变关系的代数表达依次为：

kAC=kAB=kBC. (3)

若孤立地看待这3个代数表达式,也许发现不了什么；若用联系的观点看式(1)，式(2)，可得动点A,C坐标之间的关系,即

式(3)是直线的斜率,可用点A,B,C的坐标表示,这3个点与前面的点A,C有重复,因此,可再次建立联系.若用kAC来表达,则

若用kAB来表达,则

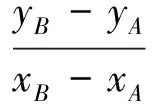
注意到式(6)的右端也与斜率有关,若设线段BP的中点为D,则kAB=kOD,结合图形知这是必然的.再次审视式(7),是变化中的不变关系,且其表达形式与解题目标一致,这也许不是偶然！

2.3 源于数学审美意识的调控

问题解决的思维过程是多种意识共同调控的结果.数学审美意识也经常参与到数学解题的过程中,比如在化简代数式时,我们会自觉地化到最简便是求简意识使然.根据题目结论,要证PA⊥PB,即证kPA·kPB=-1,代入点的坐标,此时可能还没有收获.若联系不变量kPA=2kAB,kAB由点A,B的坐标表示,注意到点B与kPB表达式中的点B为同一点(趋同意识),则点A,P对称,横纵坐标都互为相反数,方便计算(求简意识).至此,解法2便水到渠成.

3 学生为什么没想到好解法

在高考这一特定的环境下,学生想不到好的解法,原因固然很多,但主要的有2点：一是题目的背景具有迷惑性,学生的视野被题目表象迷惑致使其无法洞察问题的本质；二是学生对运动中存在的不变性这一规律缺乏认识和思考,更谈不上用之于指导思维和解题了.

3.1 呈现试题的载体和背景掩盖了题目的本质

试题以椭圆为载体,以3条动直线与椭圆的交点为背景考查垂直关系,背景和载体具有一定的迷惑性,学生易将其归结为曲线的交点问题,选择解法1也就成为自然,这在学生的访谈中得到了证实.事实上,椭圆并不是式(7)成立的必要条件,只要保持点A,P关于原点对称、点C是点P在x轴上的射影、点A,B,C共线,式(7)就成立,也就是说,式(7)对一般的椭圆、双曲线仍成立[2-3].因此,考查椭圆的性质不是目的,而是以其为载体考查学生的思辨能力,这使得该题具有很好的区分度和甄别功能,充分体现了江苏省数学高考试题“以能力立意”的指导思想.

3.2 不变量思想的缺失是根本原因

虽然,不变量思想在数学中,特别是几何学中是根本思想之一,各种不同的几何学就是研究在各种不同的变换之下的不变量.如欧氏几何和射影几何就是分别研究在刚体运动和射影变换下的不变性与不变量.可是在中学教科书里,找不到“不变量”一词,非常遗憾(张奠宙教授语).诚然如此,中学的函数概念、函数模型虽以培养学生运动变化观为目标,但其侧重点是变量之间的依存关系；函数图像的平移、对称变换、立体几何中平面图形的翻折等知识也涉及到不变关系,但由于知识模块的割裂,学生很难将其迁移到解析几何中去.而且,在中学教学实际中,不变量思想也不像数形结合、等价转化、分类讨论等数学思想那样被广泛重视,学生得到相关训练的机会少.因此,不变量思想的缺失是想不到解法2的根本原因.

4 教学反思

学生想不到好的解法,教师应从自己的教学中去寻找深层的原因,才能改进教学,做到“前车之鉴,后事之师”.

4.1 变教材为课程,教学中渗透不变量思想

重要的数学思想,在教学中没有被重视,究其原因,“不变量”是教材以外的内容！说到底,就涉及到教师的教材观和课程观——我们教的是“教材”还是“课程”？

毋庸置疑,教师不能仅是教材的执行者,而应站在课程实施者和课程改革主体的视角审视教材的内容、编排体系.要跳出学科看教学,避免学科的分类割裂了知识的广泛联系,造成学生认识的僵化和局限,妨碍学生知识能力、态度、情感的协调发展.那些既符合学生认知规律又能促进学生认知发展的知识、观点和思想,不只适用于某个学科或模块,应该在教学中适时渗透.这要求教师能选择恰当的教学时机,把静止的、学术形态的数学知识演化成与学生认知水平、思维脉络大体相当的动态的、教育形态的数学知识.比如,当学生对解析法有了感性理解后,提出问题：坐标系的不同取法,对研究结果是否有影响？可激起学生对解析法的理性思考,探究解析法中的变与不变,体会其作为数学方法的实质和精髓；再如,学习了向量后,学生都知道,它是沟通代数与几何的桥梁.

4.2 发挥课本习题功能,切实开展数学探究活动

数学探究是高中数学课程中引入的一种新的学习方式.数学探究课题的选择是完成数学探究活动的关键.那么,作为探究活动的组织者、指导者、合作者的教师,如何选好探究课题呢？

笔者认为课本中许多习题就是很好的探究课题,只要教师吃透教材,在课标的指导下对教材适当整合、适当拓展就可以开发出好的探究课题.

椭圆可以视为对圆上的点向同一条直径施行伸缩变换而成.运用椭圆与圆之间的这种关系,你能根据圆的面积公式来猜测椭圆的面积公式吗？

如果学生选修了系列4的“矩阵与变换”专题,那么，教师可以再次组织学生证明自己的猜测并提出如下问题：(1)变换前后的图形面积已知,能否大胆猜想变换前后图形面积和变换矩阵之间有什么关系？(2)圆的一些性质,如直径所对的圆周角为直角、垂径定理经伸压变换后在椭圆中的表达形式如何?

如果学生经历过这样的探究过程,那么他们可以体会到伸压变换把圆、椭圆在知识序列中相去甚远的几何图形联系在一起的；还可以激发学习的兴趣,使学生的思维触及仿射几何中的重要定理：在仿射变换下,2个图形面积之比是仿射不变量.学生收获的不仅仅是对伸压变换、椭圆的性质的深刻理解,还有认知结构的完善、认知能力的生成和情感态度的质的飞跃,学生想到解法2也就不是难事,悟性好的学生还能发现本题的题根——直径所对的圆周角为直角在椭圆中的推广！

[1] 张雪松.谈如何有效利用高考题[J].中国数学教育：高中版,2010(9):12-14.

[2] 张乃贵.探究2011年江苏高考解几第18题[J].数学通讯,2011(9):61-62.

[3] 张盛冬.2011年江苏高考第18题的新解及探究[J].考试：高考·数学版,2011(9/10):21-23.