谈几种换元法在一道高考题中的应用

● (扬州大学附属中学 江苏扬州 225000)

谈几种换元法在一道高考题中的应用

●孟伟业束荣盛(扬州大学附属中学 江苏扬州 225000)

面对一个数学问题，如果直接求解有困难，或不易下手，或由问题的条件难以直接得出结论时，往往需要引入一个或几个新“元”代换原问题中的“元”，使得以新元为基础的问题求解比较简单，解决以后将结果倒回去恢复原来的元，即可得原问题的结果.这种解决问题的方法称为换元法,又称变量代换法.换元法的基本思想是通过变量代换，化繁为简，化难为易，使问题发生有利的转化，从而达到解题目的[1].本文以一道高考试题为例，谈谈几种换元法在解题中的应用.

题目设x,y为实数，若4x2+y2+xy=1，则2x+y的最大值是________.

(2011年浙江省数学高考理科试题)

1 目标换元

在处理最值时，有时需要将要求的代数式自身看作一个未知变元，作目标换元，然后通过它建立关系式(等或不等)，并进行适当运算，从而得出未知变元的值.

解法1令t=2x+y，则

y=t-2x，

代入4x2+y2+xy=1，得方程

6x2-3tx+t2-1=0.

关于x的方程有根，故Δ≥0，即

9t2-4×6(t2-1)≥0，

解得

解法2由4x2+y2+xy=1，得

(2x+y)2-3xy=1，

即

而

即

令t=2x+y，则

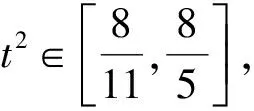
评注解法1是将问题转化为熟悉的一元二次方程问题，然后用判别式法加以解决.判别式法是解决二次问题的重要方法之一，但要注意检验.解法2是借助不等关系将所有的量都用目标表示，从而使问题得以解决.

2 比值换元

如果已知条件为比例式子或者可以看作比例，那么用比值代入可使其简化[1].本题中虽然y和x的关系并不是以比例式呈现的，但是考虑到条件是二元齐次式，故可以考虑用正比例函数(比值关系)将2个变量的依存关系揭示出来，进而将二元条件最值问题化归为一元最值来求解.

解法3令y=kx，代入4x2+y2+xy=1并整理得

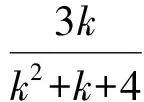
当k=0时，(2x+y)2=1.

(2x+y)2∈[0,1).

3 三角换元

解法4将4x2+y2+xy=1配方得

令

即

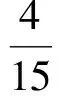
从而

即

从而 (2x+y)2=4x2+y2+4xy=sin2θ+4cos2θ=

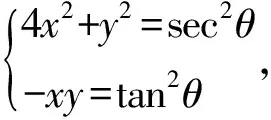
即

从而(2x+y)2=4x2+y2+4xy=sec2θ-4tan2θ=

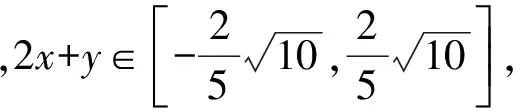
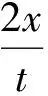
4 均值换元

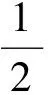
所以

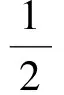
即

即

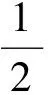
5 和差换元

若x,y∈R，则可设x=a+b，y=a-b，这种变换称为和差换元法.

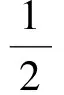
整理得

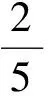
6 常数换元

很多题目的条件中会出现等于常数(通常为1，若不为1可左右2侧同时除以这一常数，即可化为1)的等式条件.若能有效地、创造性地处理常数，往往会给解题带来意想不到的方便.

解法9(2x+y)2=4x2+4xy+y2=

下面的过程与解法3相似，在此不再赘述.

评注条件是齐二次式，而目标是一次式，故考虑将目标平方，凑出二次式，然后再灵活运用常数“1”进行代换.

7 极坐标换元

方程4x2+y2+xy=1所表示的曲线方程是建立在直角坐标系基础上的，若将其置于极坐标系下来考虑，则会展现另一片精彩天地.

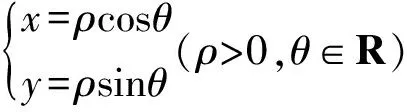
从而

t=2x+y=ρ(2cosθ+sinθ)，

即

t2=ρ2(sin2θ+4cos2θ+4sinθcosθ),

亦即

下面的过程也与解法3相似，此处略.

评注这里转换了看问题的视角，将问题置于不同的坐标系下考虑，给出了一种颇具创意的解法.这样的解法之所以有效，还是得益于条件、结论均为齐次式，否则处理的难度将变大.

至此，笔者以一道高考题为例，给出了7种换元法在这道试题中的应用.尽管换元法没有固定模式，但在分析时，若能关注条件、结论的结构特征，探索条件与结论之间的联系等，往往可以找到问题解决的突破口.当然对于这道题目的解决还有其他一些方法，有兴趣的读者可以查阅文献[3]、[4].

[1] 李明振.数学方法与解题研究[M].上海：上海科技教育出版社,2002:235-255.

[2] 陈向阳,周超.全国重点大学自主招生通用教程(数学)[M].南京：南京大学出版社,2011:16-22.

[3] 傅建红.从一道高考题看二元条件最值问题的求解策略[J].数学教育研究,2011(5):55-56.

[4] 韩天禧,张昌盛.一道高考二元条件最值问题的解法探究[J].新高考：高三数学,2012(2):28-32.