变视点卫星轨迹线投影研究

任留成

(空军指挥学院，北京100097)

变视点卫星轨迹线投影研究

任留成

(空军指挥学院，北京100097)

在太空观测地球，观测视点是随卫星运动而不断变化的。针对变视点的卫星遥感数据，设计建立卫星星下点的轨迹线投影新模型。研究内容包括地球椭球面上卫星轨迹线方程式的建立、星下点坐标的确定，以及卫星地面轨迹在变视点空间透视投影中的映像等，通过模型计算得出该投影精度小于±0.01″。

变视点;卫星轨迹线;投影

一、引 言

研究卫星轨迹线投影就是为了便于确定卫星地面轨迹的位置。卫星的地面轨迹线在图像投影的统一坐标系内可以描述为直线，也可以描述为曲线。建立卫星星下点轨迹投影可以有多种方式，但大致可分为两大类:一是先将整幅卫星图像处理成某种地图投影，当图像经过一系列的处理后转换成用户所需的常规地图投影，此时也就把卫星地面轨迹线和成像区域描绘在相应的地图上，则该条带内的卫星轨迹线也就依附于该投影模型;二是首先建立卫星的轨迹线投影，然后再以此为基础来构建同一条带的卫星图像空间地图投影。

早在20世纪70年代，国内外学者就开始对卫星轨迹线投影进行研究，建立了一系列的投影模型。现有的关于卫星轨迹线的投影主要有3种基本形式:一是圆柱投影，即卫星轨道圆柱投影;二是双正形纬线圆锥投影，包括双纬线卫星轨迹正形圆锥投影和双正形纬线卫星轨迹圆锥投影(其中一纬线为轨迹极限);三是单标纬圆锥投影，包括单正形纬线卫星轨迹圆锥投影和最接近方位投影的卫星轨迹圆锥投影。

系统程序运行方式如图6所示，系统上电以后，两个CPU系统进行初始化，STM32系统进行系统参数的调取，并进行相应配置，随时监控是否有外部数据请求，并负责发射毫米波信号。同时，以DSP28335为主的单片机系统进行毫米波信号的接收处理，最终计算出距离信息存储于双口RAM中，供STM32进行调取。

J.P.Snyder于1977年提出采用卫星轨迹圆柱投影，可以把卫星地面轨迹在地图上面绘成直线［1］，并于1981年研究了卫星轨迹圆锥投影［2］。杨启和于1989年讨论了卫星地面轨迹在投影中的映像［3］。郭树贵综述了关于卫星轨迹线投影的研究结果［4］。笔者于2003年对卫星轨迹线投影和空间透视投影进行了一些研究［5］。前苏联的布尔耶夫斯基等于1992年在其著作中对卫星单张相片的轨迹线投影问题也进行过探讨［6］。时晓燕、胡毓钜于1994年对卫星倾斜相面的外心透视投影进行了较为详细的分析比较［7］。国内外很多学者，比如R.E.Deakin，Wagih N.Hanna，对卫星轨迹线投影进行了研究［8-9］，在此不再一一赘述。

科玛嘉显色培养基、单核细胞增生李氏特菌、金黄色葡萄球菌等VITEK生化鉴定卡购自法国梅里埃公司。MYP显色养基、培缓冲蛋白胨水、SC、HE、肠道增菌肉汤（2μg/ml新生霉素）、碱性蛋白胨水、TCBS、TSI|、SIM动力培养基和生化管由北京陆桥技术有限公司生产。沙门氏菌诊断血清由兰州生物制品研究所生产，致泻性大肠埃希氏菌标准菌株由甘肃省疾控中心微生物检验科提供，均在有效期内。

本文拟设计一种新的卫星轨迹线投影模型，即变视点的卫星轨迹线投影模型，目的是解决人们在卫星上看地球，卫星运行到空间某一地点时，以该点为视点，建立一种空间透视投影，卫星轨迹线在该投影中的映像问题。

二、椭球面上的卫星轨迹线方程式

人造地球卫星在太空围绕地球运行的轨道形状是一规则的椭圆，符合动力学的“二题问题”理论和牛顿第三定律，卫星飞行满足:①卫星运行椭圆轨道的一个焦点位于地球质心;②地球质心至卫星的向经，在椭圆轨道面上所扫过的面积与时间成正比;③卫星运行周期的平方与轨道长半轴的立方成比例［10］。由此条件可确定出卫星轨道的6个根数，即卫星轨道的升交点赤经Ω(0≤Ω≤2π)、轨道平面倾角i、近地点角距ω、轨道长半轴a、轨道偏心率e，以及卫星过近地点的时刻t(如图1所示)。

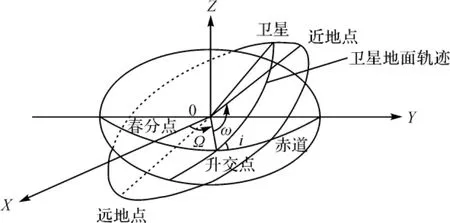
图1 卫星运行轨道几何示意图

假设地球椭球面的方程为

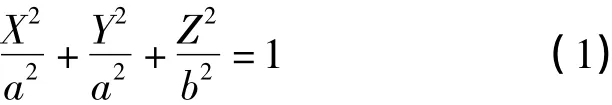
首先假设卫星是围绕静止的地球轨道飞行，设O为卫星地面轨迹由南向经过赤道的交点，假定过点O的经线为零经线，i为轨道倾角。设经过t时刻卫星地面轨迹为另一点P(φ，λ)，如图2所示。设点M为经线λ与赤道的交点。假设从O点到P点的弧线角为λ'(文献［10］中称之为变换经度)。在球面直角三角形OPM中，角∠POM=180°－i，边PM=φ，OM=λ，OP=－λ'，于是由球面三角的正弦、余弦定理得

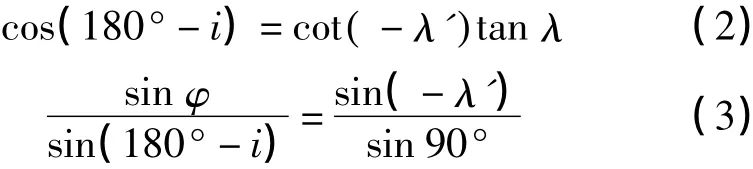
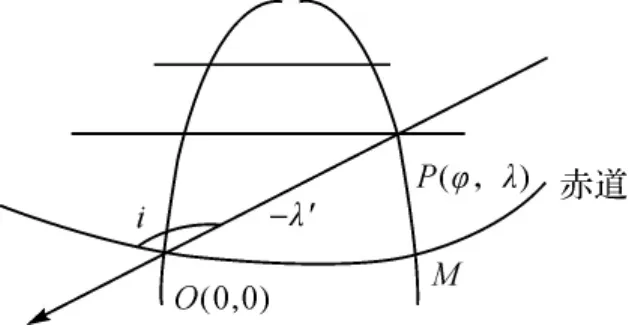
图2 球面三角形

(1)仅在预应力作用下，箱梁翼缘板上产生的正应力不均匀分布现象，仍然符合传统意义上关于剪力滞的定义，即由于翼缘板不均匀剪力流引起的，所以引用剪力滞概念来描述这种正应力不均匀分布现象是有理论依据的。由本研究得出来的结论如下：宽跨比对于箱梁剪力滞系数沿着纵向分布没有影响；腹板越来越厚时，靠近支座的剪力滞系数和剪力滞系数峰值有所减小，其他位置的剪力滞系数差别不是很大。

1.3 统计学方法 将所收集的数据由双人录入EpiData 3.1软件，统计学处理通过SPSS 22.0软件完成。计数资料以百分比表示，采用χ2检验；计量资料以x±s表示，采用t检验。以P<0.05为差异有统计学意义。

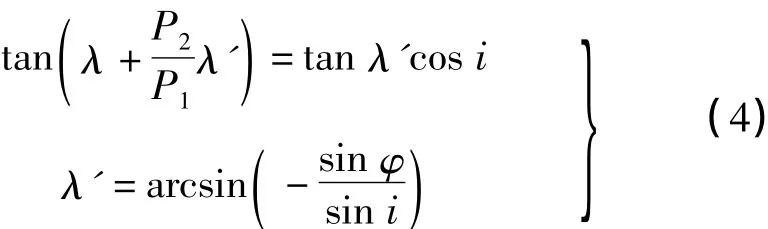
根据文献［11］可知:卫星轨道面的法向量R为假设G、P分别为向量GL、PL方向的单位向量，由于

三、星下点坐标的确定

3.2 学生满意度 为了解学生对工作坊教学模式的满意程度，对实验班的学生进行了无记名问卷调查，调查表分为两部分，第一部分为选择题：①对教学效果的满意度；②自我学习能力提高满意度；③授课方式满意度；④创新意识、创新能力提高满意度。评价等级分为三类：A代表满意，B代表较满意，C代表不满意。第二部分为主观题，简要写出心得体会。调查结果如表2所示。

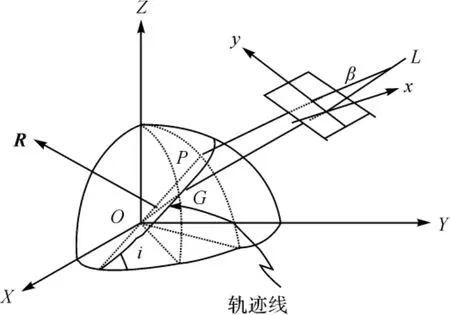
图3 变视点卫星地面轨迹示意图

易知

以τ方向为x轴建立地图坐标系，则地图坐标系中y轴上单位矢量Y为

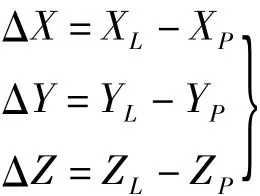
则空间任一点的直角坐标与其地理坐标的关系为

图3为地球椭球的第一卦限部分。假设: L(φL，λL，H)=L(XL，YL，ZL)为视点，H=LG＞0为卫星飞行高度，亦即从L到球面上的垂线;G(φG， λG，hG)=G(XG，YG，ZG)为L的星下点;G1为G在投影面上的对应点(即影像制图中心);φ、λ表示地球经纬度;h表示地理高程，对于卫星位置L来说h= H，对于地面点G来说h=hG或0;P(φ，λ，h)= P(XP，YP，ZP)表示地球上任一点;T为G1处与GL垂直的像平面;f为卫星摄像机焦距;P1(x，y)是地图上对应于P的点;R为轨道面的单位法向量;τ为卫星飞行方向的单位矢量。

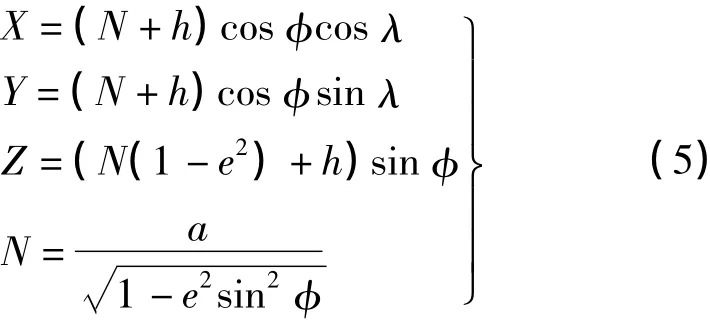
如图2所示，假定t=0时刻星下点为升交点，卫星运行时间t达到星下点G点，下面求星下点G的地理坐标。

(3)接收6种数字调制信号，实现信号下混频，获得复基带信号。根据获得的复基带信号，分别计算MASK、MPSK、MFSK的二阶、四阶和六阶累积量值，然后再计算三个高阶累积量特征参数fx1、fx2、fx3。

假设地球自转的角速度为ω=7 292 115×10－11rad/s，自转周期为P1=1440 min，卫星运行周期为P2(Landsat卫星为103.267 min)。在t时间内，地球自转的角分值为

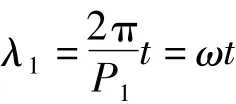
在t时间内，卫星运行的角距为

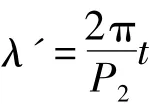
根据式(4)得到t时刻卫星地面星下点G的地理坐标与t的关系式为

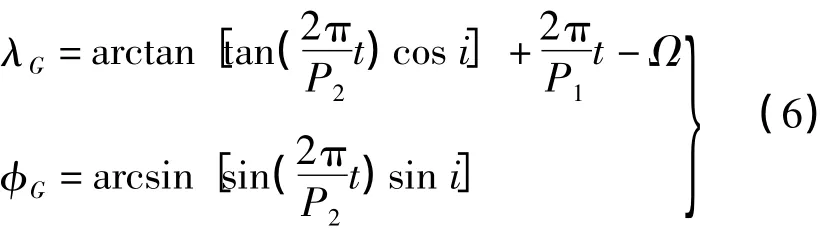
算例1:选取Ω=0，P2=101 min，i=81°。根据式(3)进行计算，当t=5 min时，φG=15.872°，λG= 1.468°;当t=10 min时，φG=31.625°，λG=2.981°;当t=20 min时，φG=62.021°，λG=16.266°。

四、卫星地面轨迹在变视点空间透视投影中的映像

如图3所示，空间任意一点L为变视点，下面利用空间解析几何理论来讨论以L为视点的空间透视投影模型的建立问题。

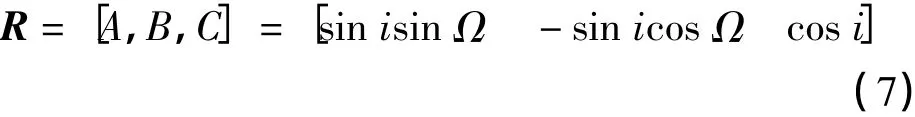
该式即为顾及地球椭球自转的卫星地面轨迹方程式。

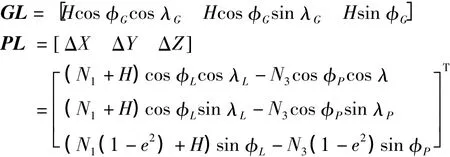
所以矢量GL上的单位矢量G和矢量PL上的单位矢量P分别为

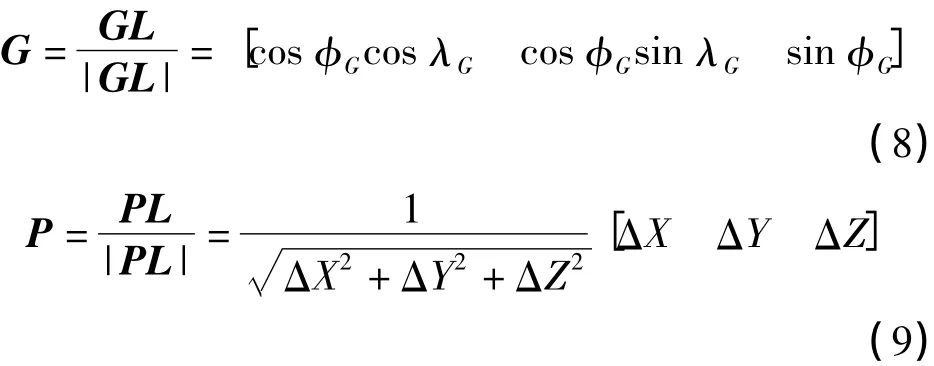
因为R与G垂直，所以卫星飞行方向的单位矢量τ为

然后再考虑到地球的自转，设卫星旋转一周的时间为P2，且地球对卫星升交点转一周的时间为P1，且地球相对于卫星轨道旋转，则在卫星从0开始到达λ'的时刻，纬圈上的纬度不改变，但从空间卫星看，子午圈将旋转，于是经度λ将改为λt(λt称为视经度)。因地球自西向东旋转，所以λ＜λt。设λt=λ+λ1，地球自转t时刻之λ1=360×60×t/P1，卫星在t时刻之，于是有将它代入中有，由此得到根据正弦、余弦定理(2)、(3)，顾及地球旋转的卫星地面轨迹方程式，参考文献［10］，最后得到

根据向量几何原理，矢量G与P的夹角β为

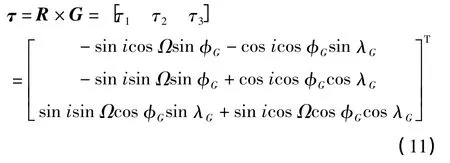
2) 基于fal函数的传统自抗扰控制的参数为：TD:r=5，h=0.2；ESO：β01=100，β02=50，β03=10；NLSEF:β1=0.3,β2=5;扰动补偿：b0=0.002 3。

所以G1P1上单位矢量P1为

在投影像平面T内，按顺时针由横坐标x轴到投影点P1的夹角为α，则

其他的药物还有荆防败毒散、感冒软胶囊、风寒感冒冲剂、小儿清感灵片、清宣止咳颗粒、小青龙冲剂、柴胡饮冲剂等，都可以在医生指导下给宝宝服用。

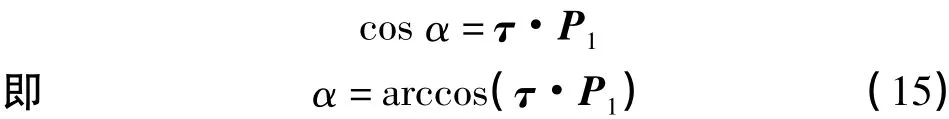
关于投影面内点P1的坐标(x，y)的计算。已知|G1L|=f，所以G1到P1的距离d为

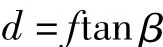
则地图投影坐标为

设W是平面GLP的单位法向量，则

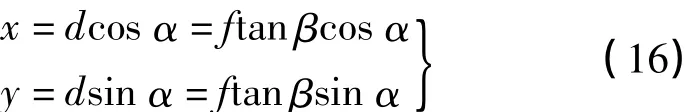
算例2:假设卫星轨道赤经 Ω=0°，倾角i= 80.908°，飞行高度为H=25 000 km，地球半径R= 6371 km，摄像机焦距f=30 cm，卫星运行周期为P2=103.267×60 s。假若卫星从升交点起飞行5 min时拍摄一张像片，选取地面点 P(φP=15°，λP= 60°)，试求P所对应的像点P1的像坐标(x，y)，结果如表1所示。

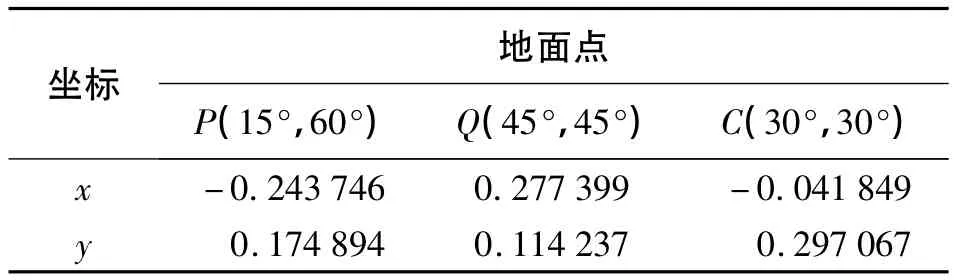
表1

图4即为按上述算例中的参数绘制的卫星地面轨迹在变视点空间透视投影中的映像。

（7）落实工作例会，探讨安全生产问题。在每个季度，都要确保能召开一定次数的安全会议。每月都要召开安全生产管理人员会议，其主要主旨是学习、传达有关安全工作的政策和文件，学习相关安全操作规范，分析当前的安全生产形势，对于企业内部近期的经验进行及时的总结，完善相关制度和措施，积极布置开展安全活动。

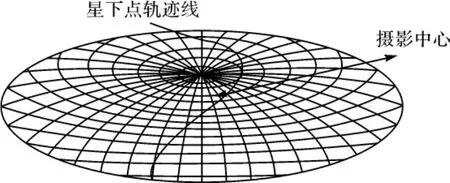
图4 卫星地面轨迹映像

五、结束语

在太空进行地球观测，所获得的卫星图像信息适合于用动态透视投影来描述，由于地球自转、卫星绕地球飞行、卫星轨道的进动和地球表面弯曲等原因，采用变视点的空间透视投影来描述更为合适。现有的卫星对地观测图像的投影模型很多都是以定视点为基准的，本文针对卫星动态获取的遥感图像，模拟卫星图像获取的物理过程，利用空间几何理论建立了卫星图像随时间变化的变视点空间透视投影模型，得到了该投影的精确表达式，利用矢量解法建立了该投影模型的正解算法及星下点坐标计算的快捷方法，进而得到了卫星轨迹线在变视点空间透视投影中的映像。通过算例知道，该投影模型具有比较精确的解算精度，精度优于±0.01″。

［1］ JUNKINS J L，TURNER J D.Formulation of a Space Oblique Mercator Map Projection［R］.Virginia:University of Virginia，1977.

［2］ SNYDER J P.The Perspective Map Projection of the Earth［J］.Cartography and Geographic Information Science，1981，8(2):149-160.

［3］ YANG Qihe，SNYDER J P，R TOBLER W.Map projection transformation—Principles and Applications［M］.London:Taylor＆Francis，2000.

［4］ 郭树桂.卫星遥感与制图［M］.郑州:解放军测绘学院，1984.

［5］ 任留成.空间投影理论及其在遥感技术中的应用［M］.北京:科学出版社，2003.

［6］ ［苏］布尔耶夫斯基，等著.单张航天像片理论［M］.林开愚，周广森译.北京:测绘出版社，1992.

［7］ 时晓燕，卢向东.倾斜相机式投影的几何解法及其与外心投影的比较［J］.武汉测绘科技大学学报，1994，19(2):118-124.

［8］ DEAKIN R E.The‘Tilted Camera’Perspective Projection of the Earth［J］.The Cartographic Journal，1990，27 (1):7-14.

［9］ HANNA W N.Vertical Perspective Projection of the Rotational Ellipsoid［J］.International Archives of Photogrammetry and Remote Sensing，1996，XXXI(4): 332-336.

［10］ 杨启和.地图投影变换原理及方法［M］.北京:解放军出版社，1989.

［11］ 刘林.人造地球卫星轨道力学［M］.北京:高等教育出版社，1992.

0494-0911(2012)S1-0032-04

P228.4

B

任留成(1963—)，男，河南汝南人，教授，博士后，主要研究方向为地图学与地理信息系统，遥感图像处理。