GPS网高程约束对二维平差精度的影响分析

康世英，张宏伟

（1.江苏华东新能源勘探有限公司，江苏南京210007;2.江苏省有色金属华东地质勘查局814队，江苏镇江212005）

一、引 言

在GPS网的二维约束平差过程中，按常规设置(仅约束控制点的平面网格坐标)时，平差结果经常不太理想，而如果同时约束起算点的大地高(或高程与高程异常之和)时，平差结果将有所不同。对于是否约束的大地高的精度影响平面平差精度问题，笔者根据多年来的实际经验，通过分析二维约束平差的转换模型，对此进行探讨分析，并提出一些参考建议。

二、二维约束平差的转换模型

GPS定位技术用于测量，其所得结果多为三维的基线向量，而基线向量又构成一个GPS基线向量网。基线向量网是三维空间的，二维转换就是提取出三维基线向量中的二维信息，构成一个二维GPS向量网。

二维转换的目的是将三维的GPS基线向量网变形投影至国家/地方坐标系上去。三维基线向量转换成二维基线向量的方法可以是在一点上实行位置的强制约束，在一条基线的空间方向上实行定向约束的三维转换方法;也可以是在一点上实行位置的强制约束，在一条基线的参考椭球面投影的法截弧和大地线方向上实行定向约束的准三维转换方法［1-2］。

GPS基线向量的二维转换分两步进行［3］。

1)GPS三维基线向量网的平移变换。设常规地面测量控制网的原点在国家大地坐标系中的大地坐标为B0、L0、H0，求得GPS网平移至地面测量网原点的平移参数为ΔX、ΔY、ΔZ，可得到GPS网中各点在国家大地坐标系中的大地坐标Bi、Li、Hi。

2)GPS网在国家大地坐标系内的二维投影变换。为使GPS网与地面网在起始方位上也一致，可利用大地测量学中的赫里斯托夫第一类微分公式(式(1))，使得同一椭球面上的网互相匹配，最后得到GPS网各点在国家大地坐标系内与地面原点一致、起始方位一致的大地坐标，进一步可算得在投影平面坐标系内的坐标xi和yi。

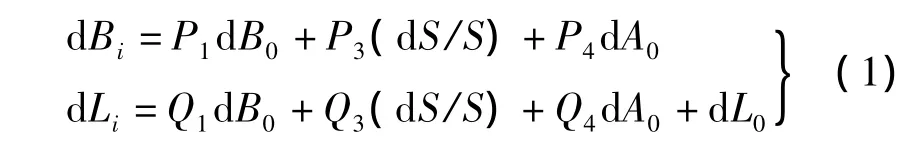
对于地方独立坐标系而言，该坐标系对应着一个地方参考椭球，该椭球与国家参考椭球只存在长半径上的差异d a，可根据椭球变换的投影公式进行投影变换得到相应的平面坐标，即

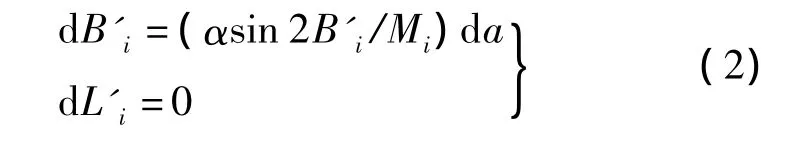
综合上述分析，二维约束平差前，根据三维和二维固定点，将WGS-84坐标系的三维基线向量转换到投影平面上的二维基线向量，再进行平差，需要至少一个三维坐标起算点和一个二维坐标起算点。二维约束平差将平面坐标分量与高程分量分离，忽略了两者之间的相关性，且对数学模型进行了一定的近似，只适用于小规模的控制网。

三、高程误差对三参数转换的影响

［4］较系统地研究了高程误差对坐标转换的影响，高程误差引起的坐标误差主要在大地高方面，对经、纬度方向的影响很小，通常只有几个毫米。在不同的区域，其影响是不同的，坐标误差随着经度的减小而增大。参考文献［5-6］中，通过数据试算及理论公式推导得出结论:若某公共点的地方坐标大地高存在误差，但求得转换参数后，转换出来点的平面坐标不变，即使公共点中多个点的大地高有误差，结果仍成立。本文采用文献［5］中同样的数据，更改大地高后进行试算，发现文献中所取4点大地高计算结果纯属巧合，其结果是有差异的，百米量级的大地高误差，其对平面坐标的影响达分米级，是超出工程允许误差的，以正常高代替大地高计算转换参数不影响待转换点的平面坐标的观点是须加条件限制的，而且对待转换点的影响随着距离起算点的增长而增大，七参数的情况也是如此。

下面举例试算，讨论以一个三维坐标作为起算点计算大地高误差对三参数转换的影响。非洲某GPS控制网(如图1所示)，表1列出了相关数据，30号点取两组大地高计算三参数，由这两组大地高求出的转换参数列于表2中。表3列出了对同一待定点(01号)利用两组转换参数求得的当地坐标。从表2、表3可看出，利用同一点取不同的国家大地坐标系大地高值所计算的原点平移参数不同，则会导致所计算的各点在国家大地坐标系中的大地坐标也不同。是否会对进行二维投影变换时产生的平差坐标存在影响，以下以天宝软件二维平差进行讨论。

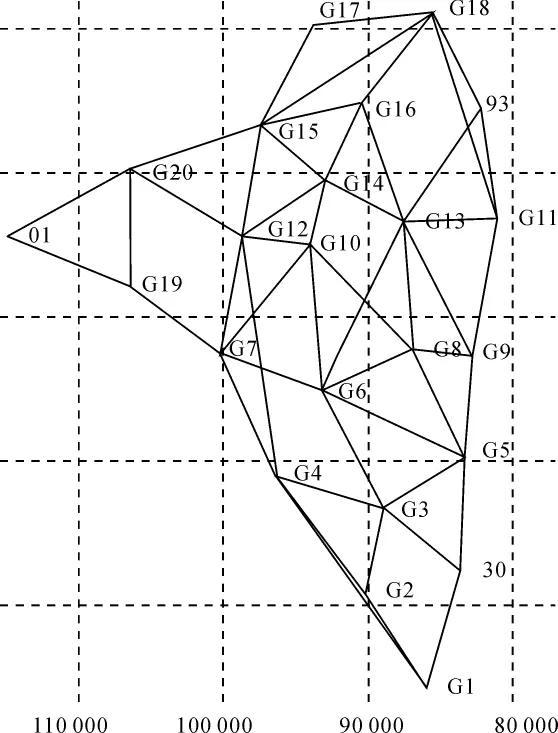
图1 某工区GPS控制网

表1 控制点的WGS84坐标和地方坐标系平面坐标 m

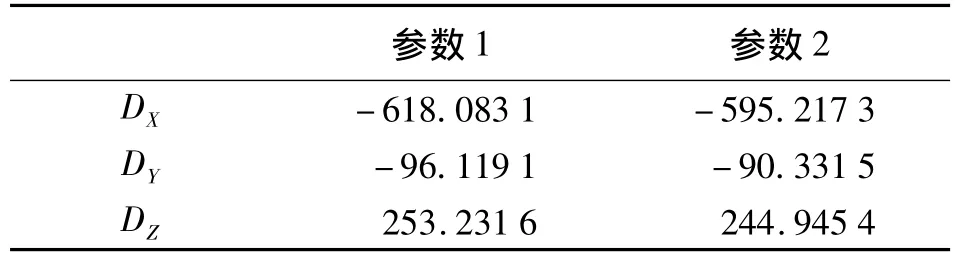
表2 对应于两组大地高求出的三参数

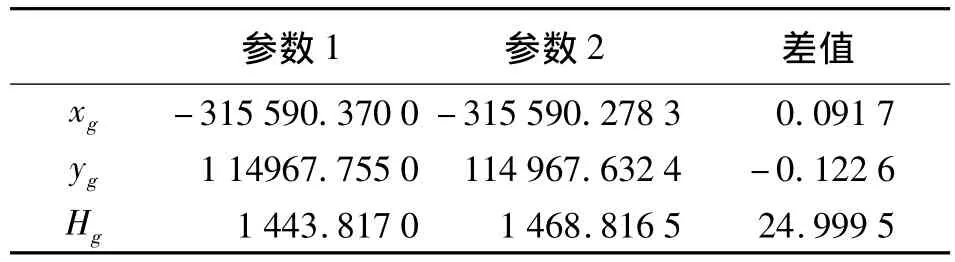
表3 两套转换参数对同一点转换结果的差异 m

四、天宝软件的二维约束平差实例分析

1.TGO1.63下的二维约束平差

在TGO1.63中，国家/地方约束平差是在建立的国家/地方基准椭球面上进行的，将GPS观测向量在项目基准上进行平差计算，通过国家/地方约束点的控制，计算出平差参数。不管项目基准中设置的基准转换如何改变，均不影响约束平差值(不管是二维还是三维平差)，因为GPS网中基准转换参数是从WGS-84转换到地方基准时产生的。每个转换组有7个平差参数:经度偏差、纬度偏差、方位角旋转、网尺度、距离比例、距离常数、高度常数，可以有选择地用来定义应用于完全约束平差期间的转换参数。

二维约束平差时，按常规设置方法约束控制点的平面坐标，无约束任何网点的大地高或约束任某一网点的大地高，则平差结果不相同，对于此问题，参考文献［7］也进行了探讨。笔者经过多次反复平差对比试验，认为出现此问题的原因与起算点距离测区的远近无关，而在于不约束任何一网点的大地高时，平差过程将不计算网尺度(默认为1)，当最少一点大地高和两个二维平面点被约束时，网尺度值才能被计算并报告出来。约束不同网点的大地高值，对平差结果亦有影响，原因在于不同网点的大地高不同，即位置重合的起算点不同，平移变换参数则不同，网尺度也不同。若约束两个网点的大地高值，则是取两点的平均变换参数;若约束3个以上网点的大地高值，则为了三维约束平差，平差结果当然存在差别。表4列出了对图1中控制网进行二维约束平差后高程影响值的对比分析结果。

表4 高程约束与否及不同高程值二维平差坐标对比表m

该GPS网无约束平差后最弱点(93)点位中误差为 ±3.5 cm;最弱边边长相对中误差为1/297 865。由此可见，GPS网观测质量良好。以30号点和93号点为平面约束点，执行地方坐标系二维约束平差，对01号点平差坐标作对比分析:①不约束任一网点的大地高时，网尺度值为1，方位角旋转值为-1.242 2″，纯量值急剧增大，控制网出现扭曲及变形;②约束30号点的大地高1时，网尺度值为1.000 018 75，方位角旋转值为-0.967 9″;③ 约束30号点的大地高2时，网尺度值为1.000 018 73，方位角旋转值为-0.968 2″。

2.TBC2.60下的二维约束平差

在TBC2.6中，约束平差完成后，7个平差参数显示在“网平差变换参数”中。约束任一网点的大地高与不约束任何网点的大地高，其二维约束平差结果基本一致。不约束任一网点大地高时，同样也计算出网尺度，结果显示:已经用内约束固定网的椭球高度(默认大地高与无约束平差结果相同)。约束任一网点的默认大地高，网尺度均相同，其平差结果也完全一致;改变任一网点的大地高，则计算出不同的网尺度，平差坐标亦不同，随着大地高误差的增大，平差坐标误差也增大。表5列出了上述GPS控制网二维约束平差高程误差影响值，对比分析:①内约束固定网的椭球高度(30号点的椭球高度为1 331.474)，网尺度值为0.999 982 589 0;② 约束30号点或93号点的大地高值，依次加上1 m、10 m、25 m、50 m、100 m、500 m 的误差，平差坐标与①对比。

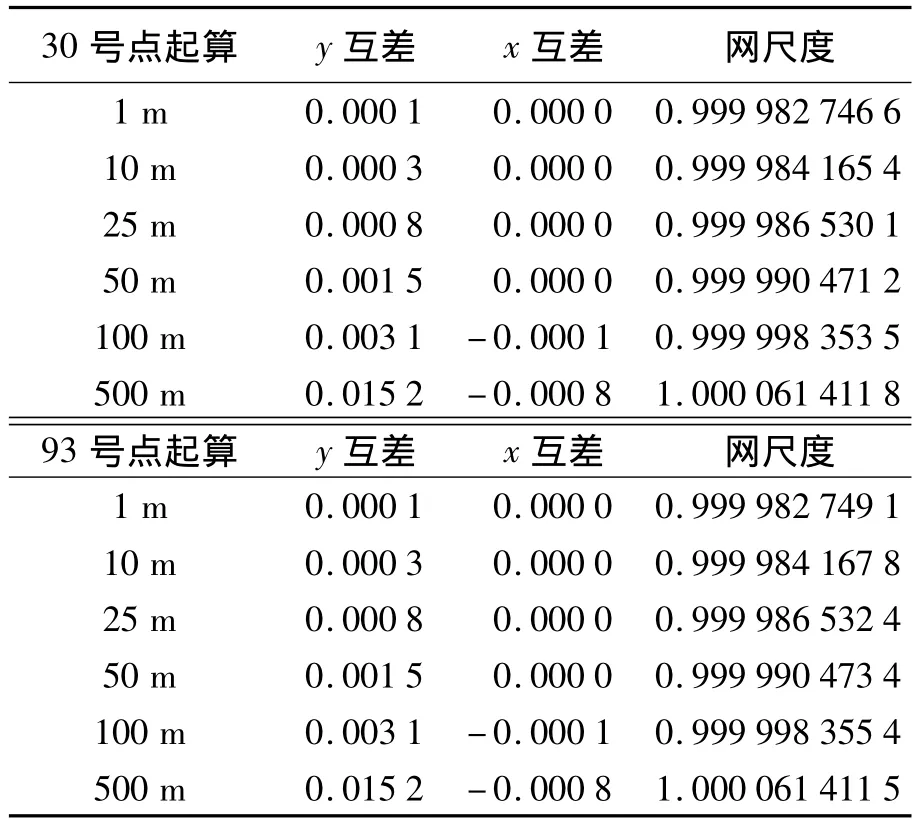
表5 不同起算点、不同高程值二维平差坐标对比表m

五、结 论

1)在进行二维约束平差时，必须以国家/地方坐标系的一个已知点和一个已知基线的方向作为起算数据，平差时将选定的三维GPS基线向量及其方差、协方差阵转换至国家/地方坐标系的二维平差计算面(椭球面或高斯投影面)，形成二维GPS基线向量及其方差、协方差阵，然后在国家/地方坐标系中进行二维约束平差［8］。转换后的GPS基线向量网与地面网在一个起算点上位置重合，在一条基线方向上方位一致。

2)在将GPS基线距离归算到参考椭球面(或测区平均高程面)和某投影面之前，须进行尺度改正计算，以消除“缩放”比例因子对平差成果的系统性影响。进行尺度改正，则至少已知一个起算点的大地高，不同的大地高数据使GPS三维基线向量网平移变换的参数改变，网尺度也改变，平差结果也将发生变化。大地高不准确不仅对高度平差有影响，而且对平面坐标也有影响，对东西坐标方向的影响大于南北坐标方向。

3)高程有25 m误差，坐标转换误差达0.1 m，但对二维约束平差最终的影响不足1 mm，100 m量级的影响值仅仅3 mm，所以二维约束平差时，用正常高来代替大地高作为起算点的高程约束，是完全能够满足工程需要的;另外，选取不同网点作为起算点，对二维约束平差的影响很小，完全可以忽略不计。

4)二维约束平差适宜于小范围的GPS控制网平差，对于不同的软件执行二维约束平差过程时，应对大地高或高程的约束问题引起重视，比如TGO。

参考文献:

［1］ 刘基余.全球定位系统原理及其应用［M］.北京:测绘出版社，1993:226-227.

［2］ 祝乃龙.GPS控制网约束平差精度探讨［J］.地理空间信息，2009，7(5):16-18.

［3］ 高成发.GPS测量［M］.北京:人民交通出版社，1999.

［4］ 张勤，王利.GPS坐标转换中高程异常误差影响规律研究［J］.测绘通报，2001(6):12-14.

［5］ 王解先，王军，陆彩萍.WGS-84与北京54坐标的转换问题［J］.大地测量与地球动力学，2003，23(3):70-73.

［6］ 王解先，邱杨媛.高程误差对七参数转换的影响［J］.大地测量与地球动力学，2007，27(3):25-27.

［7］ 李冲，谭理.利用TGO进行灾区GPS控制网平差的一种有效方法［J］.城市勘测，2010(6):93-95.

［8］ 甄登春，宁红，程小河.基于拟稳基准的GPS网2维约束平差实用方法及其应用实例［J］.测绘与空间地理信息，2008，31(5):168-171.