Moore响度的三种计算方法

焦中兴，刘 威，何岭松

（华中科技大学机械科学与工程学院，湖北 武汉 430074）

0 引言

响度是声质量评定中的重要参数，自从1933年Fletcher提出响度（loudness）概念以来，响度一直是心理声学领域的研究热点。人们建立了多种响度计算模型，其中Stevens响度计算模型[1-2]和Zwicker响度计算模型[3]都比较成功，成为1975年的国际标准[4]。然而，Zwicker模型和Stevens模型均采用图表法，在计算精度方面有所欠缺。Moore在Zwicker模型的基础上进行了改进[5-6]，其计算模型基于解析式，理论上可针对频谱、声压连续变化的声音信号进行响度计算，该模型成为了2005年的美国国家标准[7]。然而，Moore模型仅给出了可参数化描述的典型信号的响度计算方法，对现场采集的非参数化描述声音信号，必须通过FFT算法等手段提取信号的特征参数，将其转换为Moore模型能够计算的参数化描述的标准信号类型，然后才能进行响度计算。

1 用FFT算法计算Moore响度

1.1 Moore模型的运算流程

Moore模型的计算流程如图1所示，它模拟了人体听觉系统的整个过程。首先人体的头部、躯干以及人耳由于其特定的生理结构对不同频率的信号成分具有不同的放大和衰减作用。Moore模型中的外、中耳传递函数模拟了人体外耳和中耳对信号的这一滤波作用，经过外、中耳滤波处理，可以获得信号到达耳蜗的有效声压级。接下来由信号的有效声压级分布特征来确定372个耳蜗滤波器，用于模拟内耳的掩蔽机理。将信号的有效声压级作为输入，用372个耳蜗滤波器对信号进行滤波，即可求得信号的频域激励模式。根据激励大小的不同，利用相应的计算公式，便可由频域激励求得372个特性响度。将特性响度连接为1条曲线，求解曲线下的面积即为单耳响度。Moore认为双耳响度为单耳响度的2倍，所以单耳响度乘以2，即可得总响度。

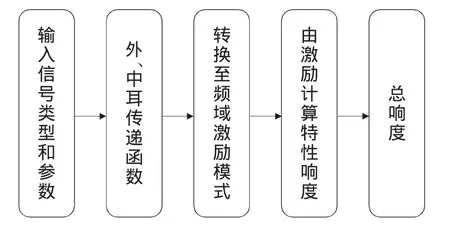
图1 Moore模型的基本流程

1.2 Moore模型需要的信号参数

根据Moore的描述，要想计算一个声音信号的响度，首先必须确定该信号的频谱。信号的频谱可以用以下4种参数化方式[7]给出：

（1）频谱由复合音信号的离散频率成分确定，则需要给出各成分的频率和声压级。

（2）频谱由几个带宽确定的噪声确定，则首先需要给出噪声的个数。这里的噪声既可以是白噪声（此处特指在通带内具有恒定的声压谱级），也可以是粉红噪声（此处特指在通带内声压谱级随频率的增加而衰减，衰减率为3dB/octave）。对于白噪声，需要给出上、下截止频率和声压谱级；对于粉红噪声，需要给出上、下截止频率和基准频率以及基准频率处的声压谱级。

（3）频谱由离散频率成分和带通噪声混合确定，前者按第（1）种方式给出参数，后者按第（2）种方式给出参数。

（4）频谱由信号的26个相邻的1/3倍频程声压级来确定，这里假设在每个1/3倍频程带内频谱都是平坦的。

其中，若信号用第（2）种方式给出，在Moore算法中还需要对其进行进一步简化处理，将频谱连续的噪声信号简化为频谱离散的复合音。简化方法：对于带宽大于30 Hz的噪声，其可以简化为一系列间隔为10Hz的纯音，纯音的声压级比其所在频率处的噪声声压谱级高10dB；对于带宽小于30Hz的噪声，可以近似为一系列间隔为1 Hz的纯音，各纯音的声压级等于其对应频率的声压谱级。若信号用第（4）种方式给出，则把信号当作26个带宽确定的白噪声，信号的简化方法同带宽大于30Hz的噪声的简化方法。

1.3 用FFT算法提取信号参数

从1.2节的描述可知，Moore响度计算的前提是以参数化方式给出的频谱，并对频谱连续的信号进行简化。所有信号最终都将被转化为参数化描述的复合音或纯音。

对于用声级计测量的声音信号，通常可以获得信号的1/3倍频程声压级，输入Moore模型就可以计算出声音信号的响度。在更多情况下，人们是用A/D卡对声音信号进行采集，要想将获取的数字信号输入到Moore模型中，需要用FFT算法进行预处理，提取信号的频谱参数。

图2是用FFT算法计算Moore响度的计算模型，其中包含了3条计算路线。计算路线1直接将FFT频谱中的谱线作为复合音中的离散频率成分来计算响度。对用44.1 kHz采样的声音信号，有文献指出可以采用44 100点的FFT算法[8-9]，以达到足够的精度。然而工程应用中，一般认为分析点数大于4 096即为大点数FFT运算。而且，FFT分析点数过多时，虽然会获得很好的频域分辨能力，但频谱谱线增多会增加计算量。所以需要分析不同FFT长度对响度计算精度的影响，以确定一个合适的FFT分析点数。

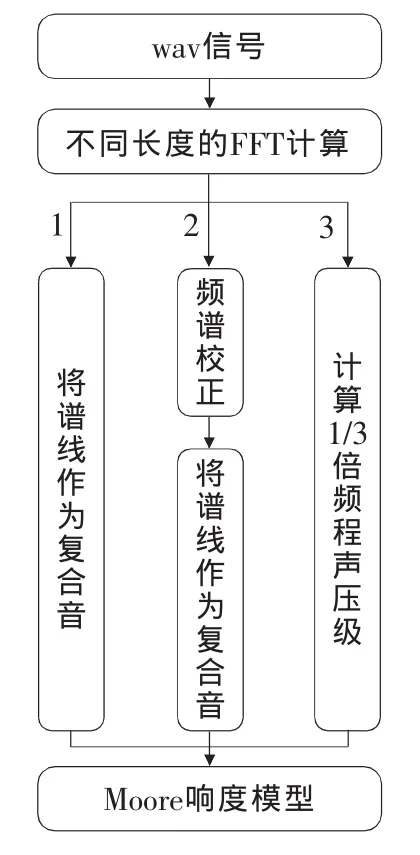
图2 用FFT计算Moore响度的方法

计算路线2将校正后频谱中的谱线作为复合音中的离散频率成分来计算响度。由于能量泄漏和栅栏效应的影响，采用FFT算法估计的纯音和复合音的频率和幅值可能会存在很大误差。例如，采用矩形窗进行FFT运算时，幅值最大误差可达36.4%[10]。采用汉宁窗，幅值误差会有一定程度的减小，并可减小旁瓣泄漏，但其影响仍然不可忽视。因此，在这里采用能量重心法[11]对频谱进行了校正，并重点分析加频谱校正和不加频谱校正对Moore响度计算精度的影响。

计算路线3先利用FFT频谱计算信号的1/3倍频程声压级，然后再计算Moore响度。这里主要是为了分析1/3倍频程处理对Moore响度计算精度的影响。

1.4 结果分析

图3（a）是频率为300 Hz，声压级为60 dB的纯音信号的响度计算结果。图中3条曲线分别表示了3种不同计算路线的响度计算结果随FFT采样点数增加的变化情况。其中，路线1的计算结果用带加号的虚线表示；路线2的计算结果用带方形符号的点划线表示；路线3的计算结果用带三角符号的点线表示。以参数化方式给定频率和声压级获得的Moore标准响度用带星号的实线表示。结果表明：对于300 Hz的纯音，不应采用1/3倍频程处理方式来计算响度，因为即使采用很高的采样点数进行FFT变换，响度结果仍有很大误差；直接用FFT频谱谱线作为复合音计算响度时，不必采用过高的采样点数进行FFT变换；采样点数过低（小于2048点）时，响度结果有较大误差，需要进行频谱校正。

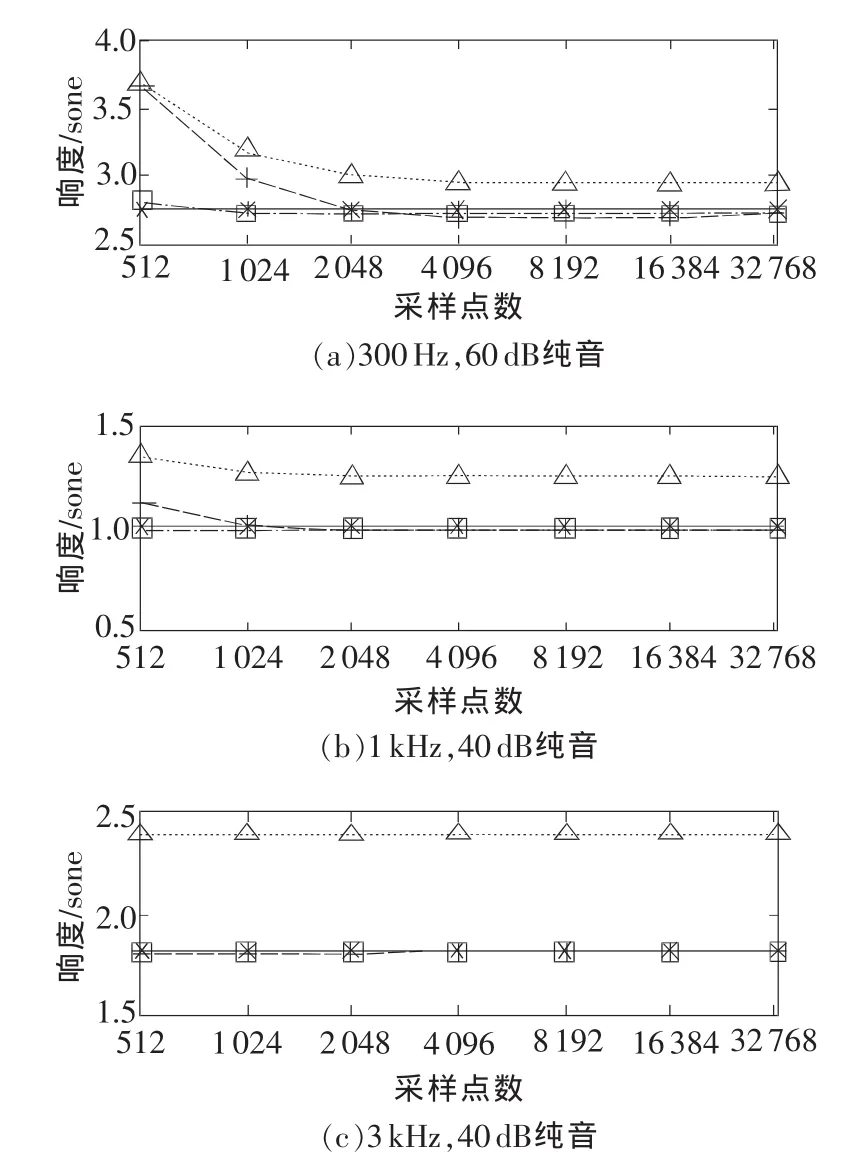
图3 纯音响度计算结果

为了进一步验证以上结论是否适用于所有纯音，计算了频率分别为1 kHz和3 kHz，声压级均为40dB 的纯音的响度，如图 3（b）和图 3（c）所示，图中曲线的含义同图3（a）。结果表明：对于纯音，确实没有必要采取过多的数据点进行FFT计算；对于频率较低的纯音，分析点数过少时，需要进行频谱校正，否则响度计算结果会有较大误差；采用1/3倍频程处理计算响度，始终会有很大误差。因此，计算纯音响度不应测量或计算信号的1/3倍频程声压级。

美国国家标准中指出Moore模型仅适用于稳定声音的响度计算，包括纯音、复合音（含和声与非和声）和不同带宽的噪声。然而对于复合音来说，当其中的某2个频率成分的频率差远小于频率均值时，响度将产生波动，称为节奏感。因此，Moore模型应该不适用于此类声音的响度计算，这里仅对频率间隔较大（≥100Hz）的复合音进行计算。图4（a）所示为频率成分为1 kHz、1.3 kHz，声压级均为60 dB复合音响度计算结果。结果显示：采用1/3倍频程处理方式计算响度，误差始终很大；采用校正谱进行响度计算，使用1 024个采样点，即可使响度结果很精确；而直接用FFT频谱计算响度，在采样点数达到8 192点时结果才很精确；图4（b）为频率成分为1 kHz、3 kHz，声压级均为60 dB复合音响度计算结果，它进一步印证了上述结论，即采用校正谱计算同直接用FFT频谱计算，可采用较少的采样点数即可达到足够的精度。

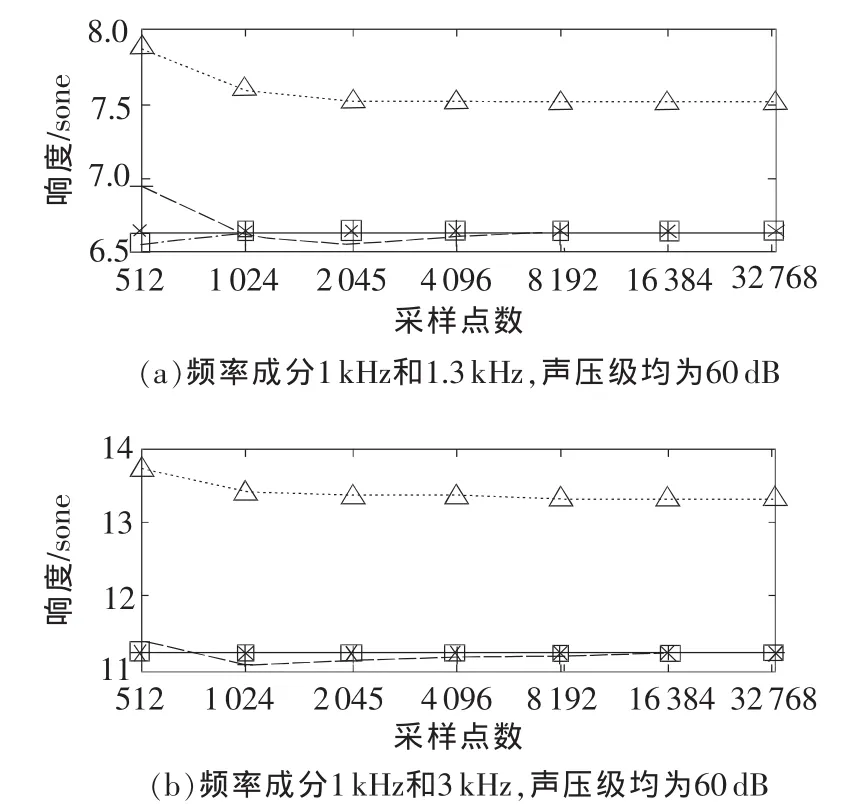
图4 复合音响度计算结果

图5（a）为频带范围为0.9~1.1kHz，声压谱级为40dB的窄带噪声响度计算结果。结果显示：无论直接利用FFT频谱作为复合音还是经过1/3倍频程处理，响度结果同Moore标准值相差均很大。分析可能的原因:Moore计算的带通噪声为具有理想频谱分布的白噪声，即用理想滤波器滤波获取的白噪声。通带之外，没有任何能量分布；通带之内，能量严格均匀分布。然而实际上这种信号是不存在的，并且这里使用的白噪声是利用巴特沃斯滤波器滤波获取的，因而其不具有理想通带。因此这里的标准响度值参照Zwicker算法给出的结果，在图中用带空心圆的实线表示。然而2种方式的计算结果同Zwicker算法结果仍相差很大，并且经过1/3倍频程处理后，误差相对更大些。

增大噪声的带宽，计算频带范围为0.75~1.25kHz，声压谱级为30 dB的窄带噪声的响度如图5（b）；频带范围为0.5~5.5 kHz，声压谱级为30 dB的噪声响度如图5（c）。观察图5可知：对带宽较窄的白噪声，2种方法计算出的响度均有很大误差，且带宽越窄，误差越大；随着带宽的增加，经过1/3倍频程声压级处理计算响度的误差相对于直接利用谱线作为复合音计算响度的误差逐渐减小，当噪声带宽较大时，计算结果误差将很小。

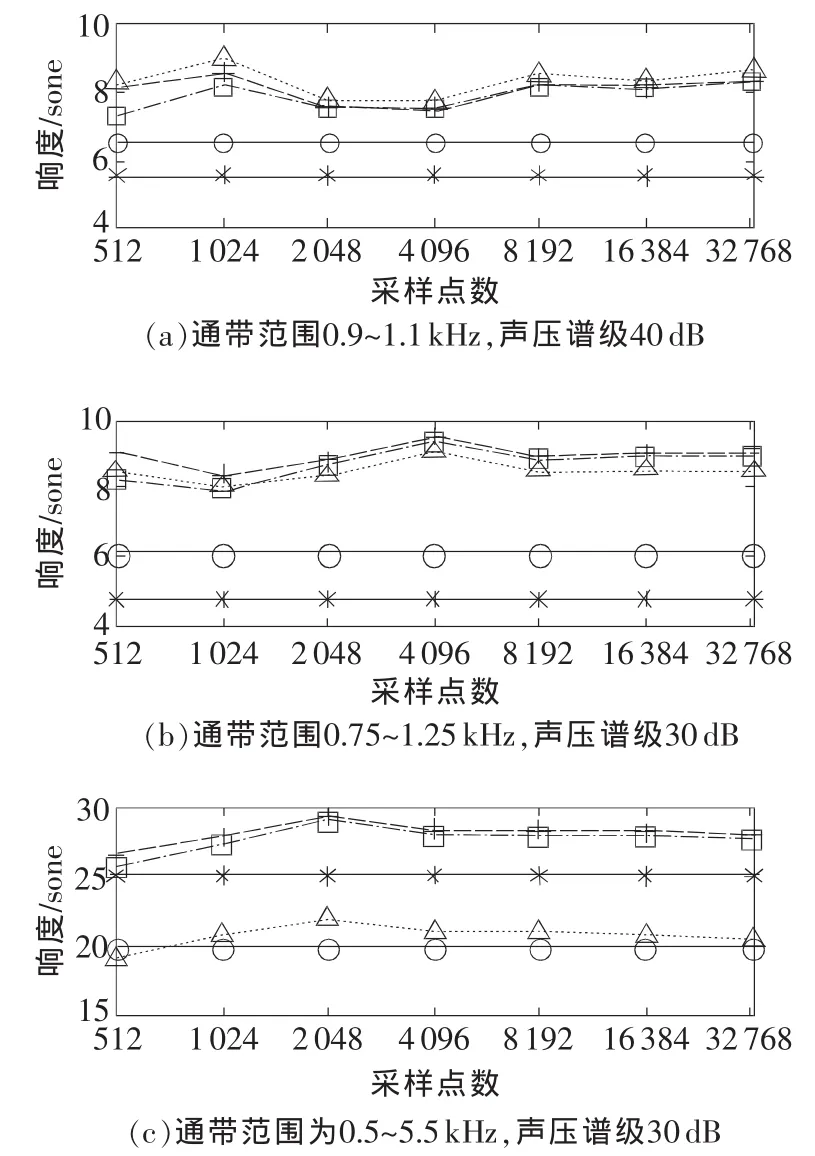
图5 窄带噪声响度计算结果

2 结束语

计算纯音或复合音的响度时，不要测量或计算信号的1/3倍频程声压级，应使用频谱谱线直接作为复合音。计算带宽较宽的信号时，应首先测量或计算信号的1/3倍频程声压级。计算纯音或宽带噪声的响度时，可以采用长度较短的FFT运算，但当纯音的频率较小时，需要进行频谱校正。为了避免频谱校正并使响度计算达到足够的精度，推荐使用的采样点数为4096。

[1]Stevens S S.Procedure for calculating loudness：MarkⅥ[J].The Journal of the Acoustical Society of America，1961，33（11）：1577-1585.

[2]Stevens S S.Perceived level of noise bu markⅦand decibels[J].The Journal of the Acoustical Society of America，1972，51（2）：575-601.

[3]Fastl H，Zwicker E.Psychoacoustics：fact and models[M].Berlin Heidelberg：Springer，2007.

[4]ISO 532—1975 Acoustic-method for calculation loudness level[S].1975.

[5]Moore B C J，Glasberg B R，Thomas B.A model for the prediction ofthresholds， loudness， and partial loudness[J].J Audio Eng Soc，1997，45（4）：224-240.

[6]Glasberg B R，Moore B C J.A revision of zwicker’s loudness model[J].Acta Acustica，1996（82）：335-345.

[7]ANSI S3.4—2005 Procedure for the computation of loudness of steady sounds[S].2005.

[8]郑文，陈克安，马元峰.Moore模型与响度计算中的关键问题[J].电声技术，2007，31（6）：11-16.

[9]马元峰，陈克安，王娜.Moore响度模型的数值计算方法[J].声学技术，2008，27（3）：390-395.

[10]谢明，丁康.频谱分析的校正方法[J].振动工程学报，1994，7（2）：172-179.

[11]丁康，江利旗.离散频谱的能量重心校正法[J].振动工程学报，2001，14（3）：354-358.