基于风洞试验的大跨度悬索桥涡振性能研究及评价

孙延国，廖海黎，李明水

（西南交通大学风工程试验研究中心，成都 610031）

0 引 言

大跨度悬索桥由于其结构轻柔、阻尼较小，主梁更易发生涡振。涡激振动一般为低风速下的小幅限幅振动，虽然不像颤振那样具有发散的性质和很大的破坏作用，但也会影响桥梁施工安全及运营期间的舒适性，严重时还会导致结构疲劳破坏。丹麦Great Belt East桥［1］、巴西 Rio－Niterói桥［2］等均出现了明显的主梁涡激共振现象，影响了桥梁结构的正常运营。在大跨度和超大跨度桥梁设计中，主梁涡激振动是一个必须加以重视的问题。抗风设计需要准确预估主梁涡激振动的振幅及发生风速，并将涡激振动振幅限制在允许范围内［3］。

现阶段研究主梁断面的涡激振动特性，主要是通过节段模型风洞试验的方法。由于常规尺度模型较小（1∶45～1∶60），雷诺数较小，且对主梁细节模拟得不够精细，可能导致试验结果（振幅及发生风速）与实桥出入较大，从而导致对实桥抗风性能的误判。Schewe、Larsen等研究了主梁断面的雷诺数效应，证明了采用小尺度的风洞试验换算到实桥进行抗风设计偏保守［4］。国内鲜荣［5］、张伟［6］等人研究了不同比例尺下桥梁断面的涡激振动性能，同样得出了小比例尺节段模型与大尺度模型存在较大的差异。采用大尺度主梁节段模型（通常为1∶15～1∶20）进行风洞试验，由于风速比接近1∶1，雷诺数与实桥的差异仅是由缩尺比引起的，并且栏杆、检修轨道等附属设施得以精确模拟，使试验结果更接近实际。由于大尺度节段模型尺寸较大，并且受风洞规模及试验段尺寸限制，风洞阻塞度对试验结果的影响不可忽视。

以某大跨度悬索桥为例，制作了主梁1∶20大比例节段模型，在XNJD－3小阻塞度风洞中进行涡振试验。结合国内外相关研究成果，分析阻尼、风迎角等因素对涡振响应的影响。考虑高阶模态的作用，并引入中国《公路桥梁抗风设计规范》［7］（公规）以及英国BS5400规范［8］（英规），对各阶振型下的涡激振动性能进行评价，为今后利用节段模型试验结果来评价实桥的涡振性能提供了借鉴。

1 涡振试验简介

涡振试验基于某大跨度悬索桥初设方案进行，该桥为双塔三跨悬索桥。主桥全长为2476m，为166m＋409m（边跨）＋1418m（主跨）＋364m（边跨）＋119m组成，主梁为闭口单箱单室箱梁断面，梁高H（中心线处）为3.5m，桥宽B为38.8m，如图1所示。

大尺度节段模型的缩尺比为1∶20，长L＝3.46m，宽B＝1.94m，高D＝0.175m，模型主要试验参数见表1。模型柱体采用优质木材制作，桥面防撞护栏、垫石采用木材加工而成，人行道护栏、检修轨道均采用塑料板雕刻而成。试验在世界上最大的土木工程专用风洞（XNJD－3风洞）中进行，试验段尺寸为22.5m×4.5m，节段模型在0°迎角时，风洞阻塞度仅为3.89%，在风洞试验允许范围以内。

图1 主梁断面Fig.1 Main girder cross section

表1 大尺度节段模型主要试验参数Table1 Main test parameters of large scale section model

图2所示为大尺度节段模型试验的模型支架及悬挂系统。为了保证模型周围流场的二维均匀流特性，在支架侧壁的前端和后端分别设置了导流风嘴。由于涡振发振风速较低，因此采用刚性较大的弹簧以提高模型的振动频率，将风速比调整至1∶1左右，这样可以获得较精细的涡振风速区，同时试验雷诺数与实桥的差异只是由缩尺比引起的，雷诺数更接近实桥。为避免弯扭耦合现象导致竖向与扭转涡振区重叠，试验中节段模型竖向与扭转频率分离开来。试验在均匀流场中进行，利用风速仪监测洞内风速，风速步长按0.2m／s进行，找到涡振区后适当减小步长。

图2 大尺度节段模型支架悬挂系统Fig.2 Support for large scale section model

2 涡振响应分析

2.1 迎角的影响

由于涡振起振风速一般较低，在低风速下会有大迎角的情况发生，因此对于成桥运营状态及施工状态进行风迎角为0°，±3°，±5°试验，对于成桥状态还特别进行了＋7°风迎角试验。为了使涡激振动现象更明显，便于涡振性能研究，试验在低于规范要求值的小阻尼比下进行试验（即图4中的阻尼系统1）。

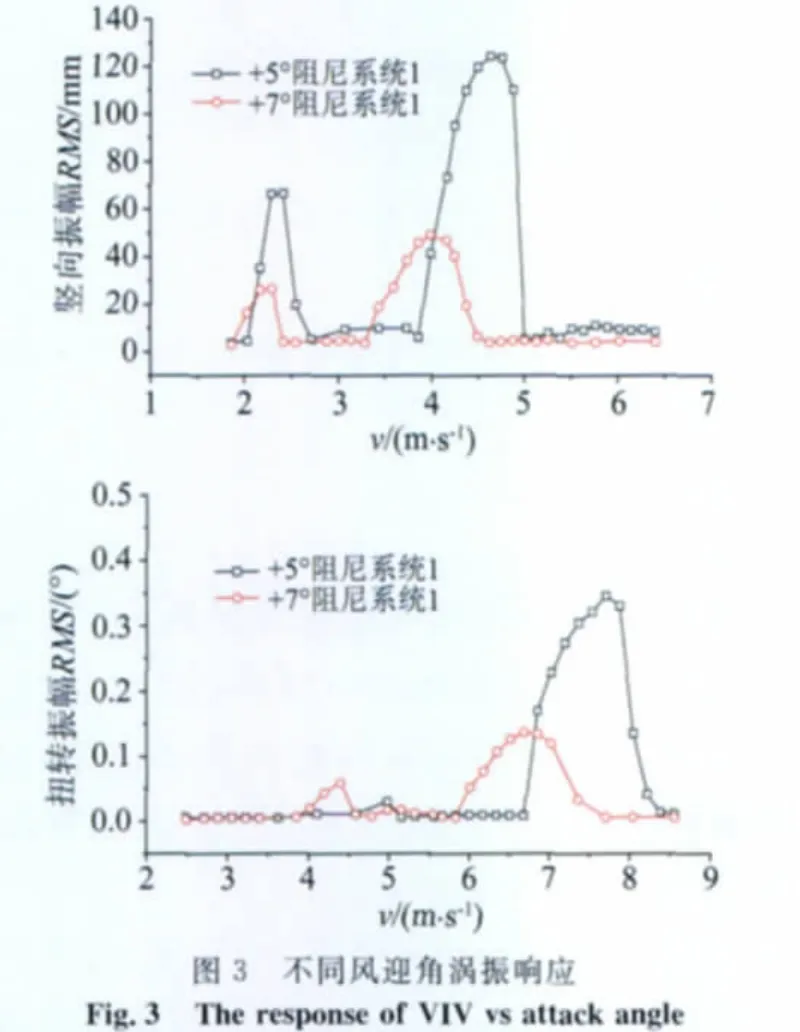
风洞试验结果表明，成桥状态主梁在0°，－3°、＋3°及－5°迎角时均没有发生明显的涡激振动现象，在＋5°及＋7°迎角时均发现了两次明显的竖向涡激振动，以及一次明显的扭转涡激振动。不同迎角下的涡振试验结果见表2及图3，图表中的实桥风速均按扭弯基频换算。结果表明，由于风迎角的变化使断面的Strouhal数发生改变，从而使涡振区发生变化，＋7°迎角时两个涡振区较＋5°均有所提前，＋5°迎角时两个竖向涡振区振幅均大于＋7°迎角时的振幅。由此可见该主梁的最不利迎角在＋5°附近，且起振风速较低，考虑来流为大迎角的情况十分必要。

表2 不同风迎角涡振响应Table2 The response of VIV vs attack angle

2.2 阻尼比的影响

为了考察阻尼比在不同规范的要求值下主梁的涡振性能以及阻尼比对涡振响应的影响，针对＋5°迎角进行了一系列改变阻尼的涡振试验。除了上述小阻尼体系外，试验还设置了由小到大4种不同的阻尼体系。由于结构体系在振动时，阻尼比并非定值，其大小与初始振幅的阻尼比有很大关系，因此本文在测量各体系的阻尼比时设置了不同的初始振幅，得出了阻尼比随振幅的变化曲线（见图4）。其中阻尼系统1为小阻尼体系，阻尼体系2及阻尼体系3与《英规》规定阻尼比（0.36%）同一水平，阻尼体系4则与《公规》规定的阻尼比（0.5%）同一水平。

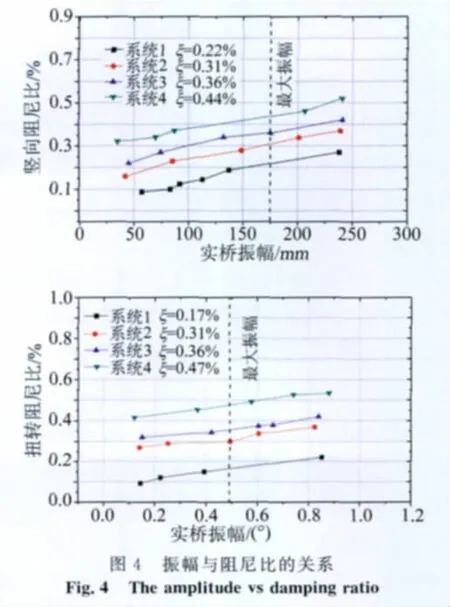
试验后发现成桥状态主梁节段模型在＋5°迎角时在阻尼系统1及阻尼系统2两种体系下均发现了明显的竖向及扭转涡激振动，在阻尼系统3时观察到的微弱的涡振现象，在阻尼系统4下，涡振现象不明显。涡振锁定区各阻尼体系下的最大竖向及扭转振幅见图5，各阻尼体系下的涡振响应见图6，可见涡振振幅对结构阻尼比较敏感，随着结构阻尼比的增加，涡振振幅和涡振区均逐渐减小。

朱乐东研究了节段模型涡振振幅向实桥换算的方法［9］，当节段模型阻尼与实桥要求阻尼出现偏差后，需对试验结果乘以阻尼修正系数Cξ＝（ξP（1－ξ2P）0.5）P／（ξ（1－ξ2）0.5）m（下标p代表实桥，m代表模型）进行修正，即实桥振幅AP＝CξAm。从该表达式可以看出由于阻尼比一般较小，可近似认为振幅与阻尼比呈线性反比关系。

由图5结果可知，两个竖向涡振区以及扭转涡振区的振幅与阻尼比均呈现较明显的线性反比关系，但在竖向第二个涡振区阻尼比较大时振幅出现波动较大的现象，这与阻尼比较大时，系统起振需要的能量较大有关系。

Khalak和 Williamson研究表明［10］，涡振锁定状态下将发生较大横风涡振响应，其振幅和涡振风速区受折减阻尼参数控制，该阻尼参数代表阻尼力与激振力之比。最具代表性的为Scruton数，SC＝4πξm／ρD2（ξ为结构阻尼比，ρ为流体密度，m为结构单位长度质量，D为结构横风特征尺寸），表明了结构阻尼特性、结构－流体质量比的联合作用效应。SC增大时，锁定状态下结构振幅减小，涡振区随之变窄。如图6所示，振幅随阻尼、SC增大而减小，涡振区亦随之变窄。但最大涡振振幅对应风速未改变，即阻尼的增大并不改变St数。目前还没有关于SC与涡振振幅、涡振区间定量关系的研究成果。

3 涡振性能评价

对于实际大跨度桥梁主梁或者细长钝体结构而言，涡激振动现象属于沿跨向范围内的三维问题，节段模型的二维特性与实桥的三维特性有显著的差别。限制节段模型试验结果直接应用到全桥主要因素是主梁沿跨向的相关性以及结构振型的影响。Ehsan结合Scanlan经验非线性模型和Wilkinson相关性函数理论推导了沿跨向主梁涡激振动振幅公式［11］，对Deer Isle－Sedgwick悬索桥进行研究发现考虑相关性及振型影响后节段模型试验结果约为实桥振幅的3倍。朱乐东引入振幅修正系数考虑了结构的振型对涡振振幅的影响，指出对于单跨悬索桥其最大幅值振型修正系数等于4／π［9］，但没有考虑涡激力沿跨向相关性对响应的影响。目前，仍没有一种成熟可靠的理论将节段模型试验结果合理的换算到实桥。为此暂不考虑相关性及振型的影响，直接将节段模型试验结果应用于主梁的涡振性能评价。

对于该大跨悬索桥梁的第一阶对称竖向、扭转模态，由于频率低，起振风速及涡振锁定风速也较低，涡振发散能量积累需要较长时间。而对于较高阶竖向、扭转模态，涡振风速较高、在高风速下能量累积较快，可能会在较短时间内激发涡振响应。因此，高阶振型同样需予以关注。

《公规》规定桥梁结构的竖弯、扭转涡激共振振幅容许值分别为：

竖向：［ha］＝0.04／fh

扭转：［θa］＝4.56／faB

式中，fh和fα分别为结构各阶竖弯及扭转频率，B为桥宽。

依照《英规》，定义反映结构振动加速度的动力敏感性的参数KD：

该规范规定，如果动力敏感性参数KD的值大于5mm／s2，即主梁因涡激振动引起的加速度过大，行人将感到不舒适，从而需对其涡振性能予以特别关注。令动力敏感性参数KD值为5mm／s2，可反算出允许振幅ymax，即ymax＝KD／f2。

试验中选取第一阶对称竖向、扭转模态，作为模型系统参数进行涡激振动风洞试验，较高阶次的涡振风速按相似比进行换算。图6为将风速换算到实桥各主要模态的涡激振动响应。表3即为每种阻尼系统下各阶模态所对应的涡振锁定风速及最大振幅以及分别根据《公规》和《英规》计算得到的容许振幅。

由表3及图6可以看出：

（1）随着结构模态的增高，涡振锁定风速也逐渐变大，此时主梁振动需要的能量变大，从第一阶对称竖弯到第二阶反对称竖弯，两个涡振区的锁定风速从2.42m／s和4.62m／s变为6.36m／s和12.15m／s，从对称扭转到反对称扭转锁定风速从7.7m／s变为8.68m／s。由桥址处风速资料可知，高阶模态下的涡振风速为桥址处的常见风速，此时能量累积较快，更易发生涡振现象。因此在进行涡振性能分析时应考虑高阶模态的作用。

（2）随着结构阻尼比的增加，涡振振幅逐渐减小，在阻尼系统1和阻尼系统2时，竖向及扭转涡振振幅均超过了《公规》及《英规》的容许值。在阻尼3时，振幅较小，竖向振幅同时满足两种规范的要求，扭转振幅满足《公规》的要求，但超过了《英规》所规定的容许振幅。

4 结 论

通过1：20大尺度节段模型风洞试验及结果分析，可得到以下主要结论：（1）不同风迎角下的涡振试验表明，在＋5°及＋7°时发生了竖向及扭转涡激振动，且＋5°时的振幅大于＋7°时的振幅，主梁的最不利风迎角范围在＋5°左右，涡振性能与来流风迎角关系密切；（2）涡振振幅对结构阻尼比的变化很敏感，涡振振幅、涡振区的范围随阻尼比的增大而减小，两者呈一定的线性反比关系；（3）低阶模态起振风速较低，需予以关注。随着结构模态阶数的增高，涡激振动的起振风速及锁定风速也增高，此时能量累积较快，可能会在较短时间内激发涡振响应，同样应予以关注；（4）《公规》在低阶模态时的容许振幅低于《英规》，随着模态阶次的增高其容许振幅逐渐高于《英规》，即《英规》对高阶模态的振幅要求严格，而《公规》对低阶模态的要求较严格。

因此，在对大跨悬索桥进行涡振性能评价时，无论从结构的阻尼水平还是结构的容许振幅方面，仅参照《公规》的相关规定对桥梁的涡振性能进行评价对结构运营甚至结构安全是不利的，应综合考虑结构阻尼、低阶及高阶模态对涡振性能的影响，见表3。

表3 各阶模态对应的涡振响应Table3 The response of VIV vs mode

［1］ FRANDSEN J B.Simultaneous pressures and accelerations measured full－scale on the Great Belt East suspension bridge［J］.Journal of Wind Engineering and Industrial Aerodynamics，2001，89：95－129.

［2］ BATTISTA R C，PFEIL M S.Reduction of vortex－induced oscillations of Rio－Niteroi Bridge by dynamic control devices［J］.Journal of Wind Engineering and Industrial Aerodynamics，2000，84：273－288.

［3］ 项海帆.现代桥梁抗风理论与实践［M］.北京：人民交通出版社，2005.

［4］ SCHEWE G，LARSEN A.Reynolds number effects in the flow around a bluff bridge deck cross section［J］.Journal of Wind Engineering and Industrial Aerodynamics，1998，74／76：829.

［5］ 鲜荣，廖海黎，李明水.大比例主梁节段模型涡激振动风洞试验分析［J］.实验流体力学，2009，23（4）：15－20.

［6］ 张伟，魏志刚，杨永昕.基于高低雷诺数试验的分离双箱涡振性能对比［J］.同济大学学报（自然科学版），2008，36（1）：7－11.

［7］ 公路桥梁抗风设计规范（JTG／YD60－01－2004）［Z］.北京：人民交通出版社，2004.

［8］ Design manual for roads and bridges（Part 3）BD 49／01 Design rules for aerodynamic effects on bridges［Z］.May，2001.

［9］ 朱乐东.桥梁涡激共振试验节段模型质量系统模拟与振幅修正方法［J］.工程力学，2005，22（5）：204－20.

［10］ KHALAK A，WILLIAMSON C H K.Dynamics of a hydro elastic cylinder with very low mass and damping［J］.Journal of Fluids and Structures，1996，10（5）：455－472.

［11］ EHSAN F，SCANLAN R H.Vortex－induced vibrations of flexible bridges［J］.Journal of Engineering Mechanics，1990，116：1392－1410.