气液两相分层流剪切应力的不确定度分析
刘夷平,王汝金,陈 超,王 经
(1.上海市计量测试技术研究院 热工与能源计量技术研究所,上海 201203;2.合肥通用机械研究院压缩机技术国家重点实验室,合肥 230088;3.上海交通大学 机械与动力工程学院 工程热物理研究所,上海 200240)
0 引 言
研究水平气液两相流流型转换以及预测持液率和流动压降,大多采用Taitel-Dukler的经典方法,他们从动量方程出发,通过适当简化,提出了凸显两相流动特征的一维双流体模型[1]。但是,该模型在不同流型区域预测持液率会出现低估或高估,而且需要额外提供本构关系式来封闭求解方程(其中重要的本构关系包括:流体-壁面相互作用和两相流体之间的相互作用),这些本构关系大多是基于实验的经验公式。虽然求解过程直接而普适,但是由于方程的非线性关系,不方便对本构关系做有效的误差分析。结果偏差必然导致研究者无法准确预测流型转变的临界条件和其他动力学参数。
基于水平气液两相分层流的实验数据,计算了液壁、气液间剪切应力的不确定度。根据最大不确定度原理,对影响其准确度的因素进行误差分析。剪切应力是计算各相摩擦因子的前提,从实验数据分析中提出有关液壁、气液界面摩擦因子的经验关系式。
1 求解方法和不确定度表达
1.1 两相流动量平衡
由于无法直接测量气液界面的剪切应力,一般的做法是从可测参数通过一维动量平衡方程间接求得。根据分层流理想化模型,如图1所示,水平圆管内充分发展气液两相动量平衡可以用以下两式表达:

Taitel和Dukler[1]对两相流体引入摩擦因子fG和fL并采用传统方式处理流体和壁面以及气液界面的剪切应力:
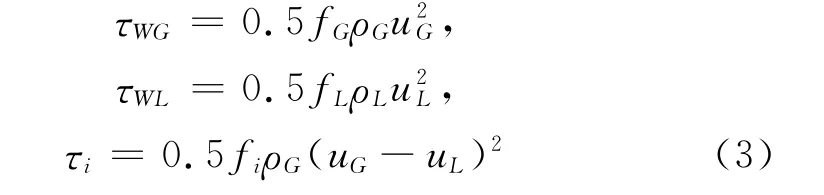

图1 水平管气液分层流动的参数示意图Fig.1 Definition of the geometrical parameters for idealized stratified pipe flow
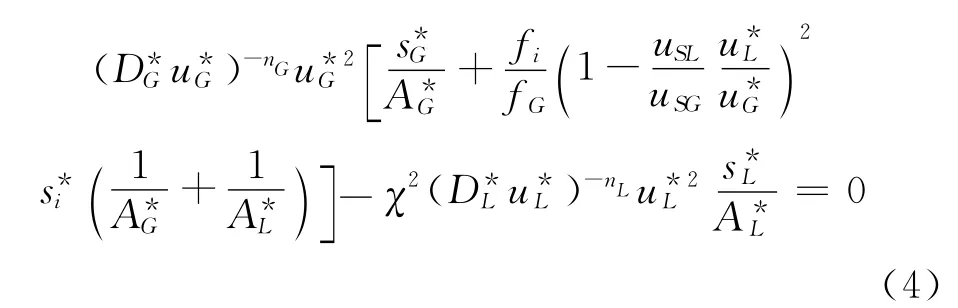
其中χ是Locakhart和Martinelli(1949)引入的无量纲参数[2],和两相流率、流体性质和管径有关。
表1中所有的无量纲几何参数、两相无量纲速度u*G、u*L都仅和θ(液相界面张角(图1))有关,而无量纲液层高度h*L=0.5(1-cosθ),那么,方程(4)仅包含3个未知量:无量纲液层高度h*L、代表体积流量的液相表观速度uSL和气相表观速度uSG。无论是流型转变预测还是求解动力学参数,一旦已知其中之二,都需要通过方程(4)求解第三个未知量。写成无量纲形式,是为了突出方程中仅有的本构关系:fi/fG。Taitel和Dukler令fi≈fG,他们认为即使对于波状分层流,使用这一假设所带来的误差也不大,从而方便求解。然而,很多文献都指出这一假设会导致持液率和压力梯度出现低估。事实上,对于给定的Martinelli数χ,持液率(或液层高度)随fi/fG比值的增大而减小[3]。多年来,研究者通过大量实验测量气壁和气液剪切应力,再由式(3)求得各摩擦因子的修正关系式[4-5]。根据测量不确定度理论,分析其中主要待测量——剪切应力。

表1 无量纲流动和几何参数Table1 Non-dimensional parameters
将表1中的无量纲几何关系代入式(1),可得界面剪切应力为:

由式(5)可知,如果确定τWG,通过测得的轴向压力梯度和液层高度,得到界面剪切应力τi,进而由式(6)得到液壁剪切应力τWL。

1.2 剪切应力的不确定度分析
在估计导出量的标准不确定度中,需考虑各被测量的不确定分量的相关性,如果将明显相关的分量做了不相关处理,结果是合成的标准不确定度偏小。为了不失相关性,按照最大不确定度(相关系数为1)分析:

界面剪切应力的不确定度为:

各敏感系数为:
洋葱的霜霉病主要危害其叶片。在病害发生初期会由外叶开始,并呈现由下向上的发展趋势,在发病过程中逐渐向内叶蔓延。发病较轻的时候洋葱会出现苍白绿长椭圆形或者长条形的病斑,随着病斑的扩大,叶身将逐渐枯折,在发病较为严重的时候甚至会痴线干枯或者腐烂的情况,对于幼苗有很大的危害。

类似地,液壁剪切应力的不确定度为:

各敏感系数为:

本文数据取自Kowalski的实验[6],他使用热膜风速仪测量了气壁剪切应力和雷诺剪切应力,并使用动量平衡法间接测量了气液界面剪切应力,该方法和步骤简述如下:
(1)实验可测量包括两相表观速度uSL和uSG,平均液层高度hL,压力梯度dP/dx和气壁剪切应力τWG,共5个;
(2)表1中所有量都可以通过实验测量值hL得到,特别是液相和气相的实际速度uL和uG也可求得;
(3)从式(5)和(6)得到τi和τWL,由式(3)计算两个摩擦因子fi和fL。
至此,获得剪切应力和摩擦因子的实验数据,用于不确定度分析。
(1)轴向压力梯度的不确定度
实验使用Miraiam U型管压力计,NIST认为,作为一种操作简单的标准测量器具,准确度仅仅取决于液柱高,其测量不确定度为最小分度的1/2。该压力计的分辨率为0.05mm水柱,所以测量不确定度为0.49Pa,两段取压口相距2m,所以轴向压力梯度的测量不确定度为0.25Pa/m。
(2)气壁剪切应力的不确定度
Kowalski使用热膜风速仪沿周向从管顶(0°)到气液界面(130°)附近,每隔30°多次测量气壁剪切应力,由于液面波动的影响,最大分散性发生在气液界面处,如图2所示,其中当处于最小平均气壁剪切应力τWG=0.037Pa(uSL=0.05m/s,uSG=1.97m/s)时,误差条范围±0.025τWG。取0.05τWG作为气壁剪切应力的不确定度。

图2 沿管壁周向测得的气壁剪切应力Fig.2 Gas wall shear stress profile along the circumferential wall(uSL=0.05m/s,uSG=1.97m/s,τWG=0.037Pa)
(3)液层高度的不确定度
Kowalski使用电导探针测量波动液面,做积分平均取得平均液层高度。根据Kordyban的假设[7],液层类似于正弦波上下波动,如图3所示,均方根波高hRMSL表达为式(16),可以认为液层在波峰幅度(Peak amplitude)范围内随机波动,故无量纲液层高度的不确定度u(h*L)由式(17)计算。


图3 液层波动时序示意图Fig.3 Instantaneous liquid height profile
2 结果和讨论
表2分别列出测量数据和结果。
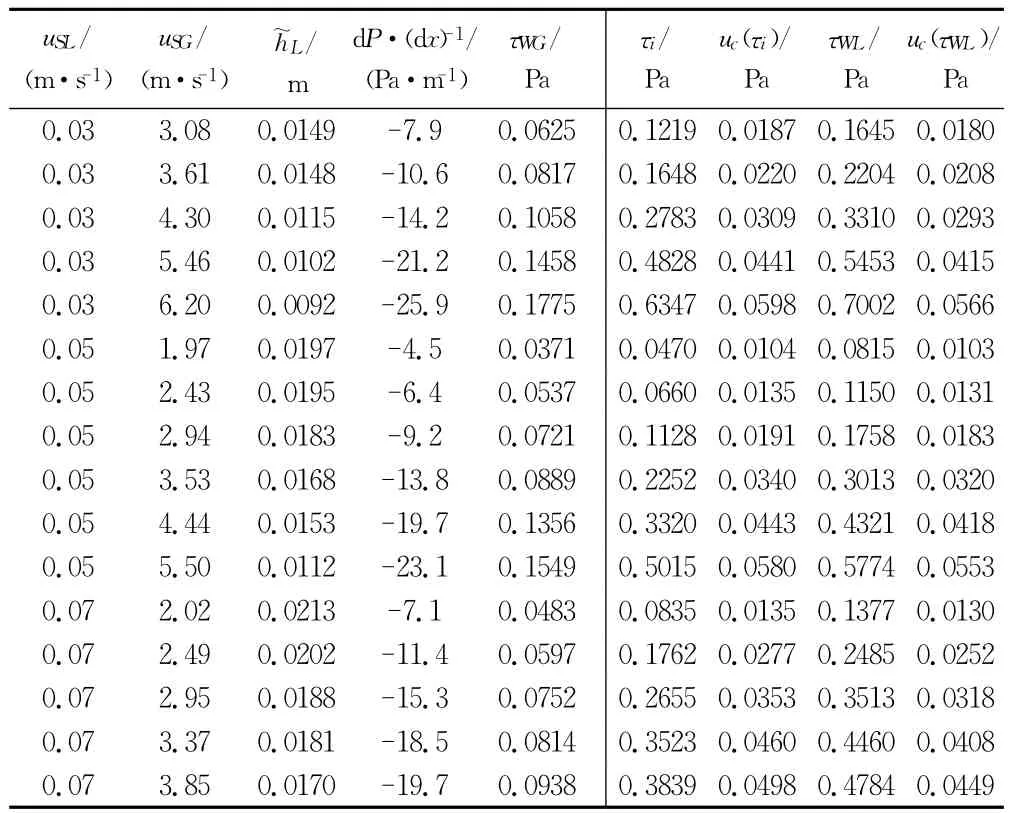
表2 测量数据(左栏)和结果(右栏)Table2 Measurement data(left)and results(right)
气液界面剪切应力的相对不确定度和各个不确定度分量如图4(a)所示,τi最小时(0.047Pa)相对不确定度最大,约为22%,随着气速增加,界面剪切应力增大,而τi的相对不确定度逐渐减小至9.13%。当两流体之间相对速度(因而τi)较低时,即便使用高准确度的压力计,压力梯度分量仍然是界面剪切应力误差的主要来源(占61.5%),而随着气速增加,其对不确定度的贡献减弱。值得注意的是,液层高度不确定度随着τi由小增大,在高τi区域贡献了最大部分的不确定度,最高占整个不确定度的66%~68%。这表明,液层高度和压力梯度测量数据是影响气液界面剪切应力的主要误差源。而气壁剪切应力τWG一般占有最少的不确定度份额,很少成为不确定度的最大贡献者(仅有4点,其所占的份额仅有40%~45%)。Andritsos[8]和Kowalski等人的实验数据已经说明,使用单向管流的Blasius方程及其平衡水力直径关系计算的气壁摩擦因子和实验结果很吻合,只是在高气相Reynolds数区域(环状流,界面波和液滴变形较为显著的区域),Blasius关系式给出的预测结果出现一些低估。这和分析相符,即以气壁剪切应力(摩擦因子)作为本构关系的出发点,利用动量平衡关系进行求解不会带来很大的误差。

图4 气液界面剪切应力和液壁剪切应力的不确定度分布图Fig.4 The uncertainty distribution of gas-liquid interface and liquid wall shear stresses
液壁剪切应力的不确定度分布(图4(b))显现出明显的差异,最大的不确定度是气液界面剪切应力贡献的,尽管液层高度和压力梯度通过τi间接影响τWL的不确定度,但是液壁剪切应力最终的误差却和他们没有直接关系。如图5所示,Kowalski给出的液壁摩擦因子和持液率及液相雷诺数关系式fL=f(εL,ReL),和实验数据不太吻合,在对数坐标中,数据并没有呈现出明显的线性关系,这说明液壁摩擦因子和液相无量纲特征参数之间不是一个类似于Blasius方程的指数型关系。

图5 液壁摩擦因子fL和持液率-液相雷诺数的关系Fig.5 The function between liquid wall friction factor fLand liquid phase holdup-Reynolds

图6 液壁摩擦因子随气相表观速度发生的转捩Fig.6 The function between liquid wall friction factor and gas superficial velocity at the transition of flow regime
对于给定的液相表观速度,液层高度随气速增加而降低,Kowalski关系式描述的液壁摩擦因子随气速缓慢上升,事实上,气液界面从光滑转变为涟漪波时,液壁摩擦因子出现突增(图6),这意味着气液剪切应力增加了液流的湍流耗散,当气速继续增加,出现大振幅波,平均液层高度降低,液流的湍流耗散减弱,液壁摩擦因子减少,Kowalski的关系式没有考虑到气相速度通过气液剪切应力对液相部分带来的影响,因而和实验数据偏离较大。根据Andritsos和Kowalski等人的分析,气液界面摩擦因子和平均液层高度、气相雷诺数、液相雷诺数有关联,而分析表明液壁剪切应力的不确定度主要是由气液界面剪切应力所贡献,那么液相摩擦因子必须结合气液界面摩擦因子才能和各相流动特征参数建立关联。通过非线性回归,得到如下关系式。图7表明计算结果和实验数据吻合,偏差在±12%以内。
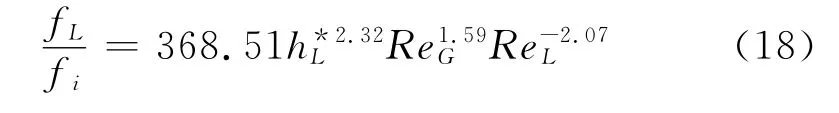
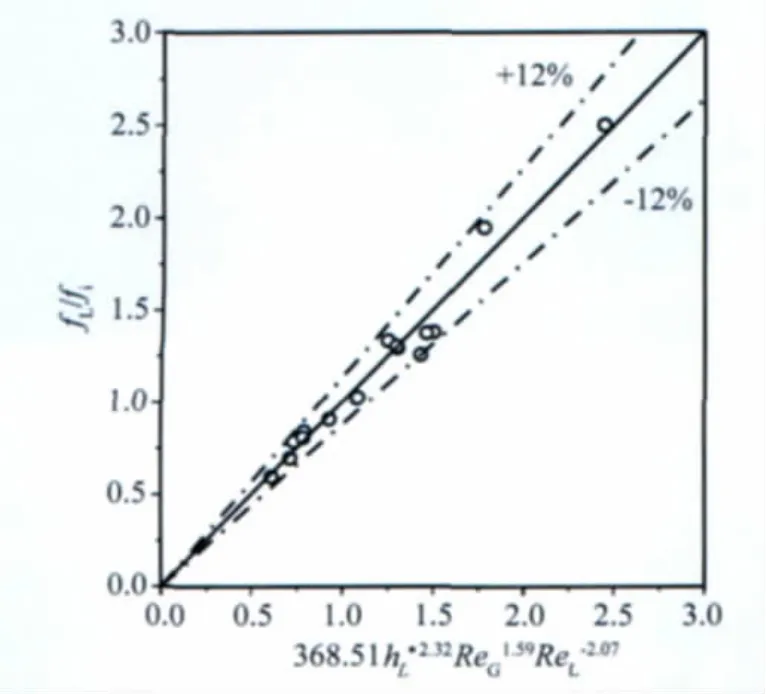
图7 式(18)计算的摩擦因子比值和实验数据的比较Fig.7 Friction factor ratio obtained by Eq.(18)in comparison with the measurement data
3 结 论
气液分层流中各相剪切应力是两相流动方程本构关系的直接来源,利用不确定度对各个影响分量作了分析。结果表明:液层高度和压力梯度的测量是气液界面剪切应力误差的主要来源,使用单相管流关系式计算的气壁剪切应力对最终的结果影响不大,而液壁剪切应力受气液界面剪切应力的影响较大,并且液壁摩擦因子很难用单相管流的指数型关系式来描述,所以将液壁和气液摩擦因子结合起来建立一个有效的关联,结果表明该关系式的计算结果和实验数据比较吻合。
[1] TAITEL Y,DUKLER A E.A model for predicting flow regime transitions in horizontal and near horizontal gasliquid flow[J].AIChE J.,1976,22(1):47-55.
[2] LOCKHART R W,MARTINELLI R C.Proposed correlation of data for isothermal two-phase two-component flow in pipes[J].Chemical Engineering Prog.,1949,45:39-48.
[3] 刘夷平,张华,王淑华.一种改进的方法预测水平气液两相流的持液率[J].工程热物理学报,2008,29(8):1131-1134.
[4] HURLBURT E T,HANRATTY T J.Prediction of the transition from stratified to slug and plug flow for long pipes[J].Int.J.Multiphase Flow,2002,28(5):707-729.
[5] ULLMANN A,ZAMIR M,GOLDSTEIN A.Closure relations for the shear stresses in two-fluid models for laminar stratified flow[J].Int.J.Multiphase Flow,2004,30(7-8):877-900.
[6] KOWALSKI J E.Wall and interfacial shear stress in stratified flow in a horizontal pipe[J].AIChE J.,1987,33(2):274-281.
[7] KORDYBAN E.Interfacial shear in two-phase wavy flow in closed horizontal channels[J].J.Fluids Engineering,1974,96(2):97-102.
[8] ANDRITSOS N.Effects of pipe diameter and liquid viscosity on horizontal stratified flow[D].Ph.D.thesis.Urbana:University of Illinois,1986.

