缺失数据下基于EM算法的GPS高程拟合*

林东方 宋迎春 杜 琨 肖琴琴

(中南大学地球科学与信息物理学院测绘与国土信息工程系，长沙 410083)

缺失数据下基于EM算法的GPS高程拟合*

林东方 宋迎春 杜 琨 肖琴琴

(中南大学地球科学与信息物理学院测绘与国土信息工程系，长沙 410083)

GPS高程拟合常因观测条件限制，部分重要拟合点的数据无法获取，致拟合数据缺失或数据量不充足。采用常规方法拟合，会降低似大地水准面的拟合精度。应用EM算法，添加了有益于高程拟合的“潜在数据”，即缺失数据的条件期望，有效提高了缺失数据下的GPS高程拟合精度。

缺失数据;EM算法;高程拟合;平面相关拟合;二次曲面拟合

1 引言

高程系统包括大地高、正高和正常高系统。大地高系统的基准面为参考椭球面，正高系统的基准面为大地水准面，而正常高系统以似大地水准面为基准面。我国规定采用正常高高程系统作为我国高程的统一系统［1］。GPS高程观测数据为大地高系统下的高程数据，由于基准面的不同，大地高系统与正常高系统存在一定的差距称为高程异常。GPS高程数据需要进行高程拟合，将大地高高程转换为正常高高程。

平面相关拟合法和二次曲面拟合法是GPS高程拟合的主要方法，平面相关拟合法认为水准面为一平面适用于小区域的拟合，二次曲面拟合法认为水准面为二次曲面，观测区域较大时，拟合效果明显优于平面相关拟合法［2］。两种拟合方法同时也受到拟合点数据量和点位分布的影响［3］，若拟合点足够多且分布均匀，则有益于水准面的拟合。观测条件的限制(如GPS无信号、环境恶劣水准测量无法进行、控制点被破坏或找不到)会造成部分重要的拟合点无法观测。缺失数据则直接影响水准面的拟合效果，降低GPS高程测量精度。对于缺失数据的处理，国内外学者通常选择的方法是只应用剩余的数据进行拟合，这样降低了水准面拟合的准确度，或者采用内插方法补充数据，结果并无太大改进［4］。EM(Expectation-Maximization)算法［5-8］是用于非完全数据参数估计的一种有效方法，它是一种数据添加算法，即在观测数据的基础上添加一些“潜在数据”，利用对数据处理有益的潜在信息，得到数据缺失下参数的最优估计。当观测数据不完全时，可以利用观测数据所服从的一些规律，对缺失数据的取值范围加以限制，即采用EM算法，利用缺失数据在现有条件下的期望值，对不完全数据进行处理计算，最终可以得到一个很好的参数估计结果。

2 EM算法及其在缺失数据下的GPS高程拟合方法

2.1 EM算法

EM算法是一种迭代算法，它的每一步迭代由两步组成:E步(求期望)和M步(极大化)。E步在给定己观测到的数据和现有参数下，求“缺失数据”的条件期望;M步计算参数的MLE估计，这与己知似然求参数的MLE估计的计算方法一致。

具体地讲，我们以P(θ/Y)表示θ的基于观测数据的后验分布密度，称为观测数据后验分布;以P (θ/Y，Z)表示添加数据Z(缺失数据)后得到的关于θ的后验分布密度函数，称为完全数据后验分布;P (Z/θ，Y)表示在给定θ和观测数据Y下潜在数据Z (即缺失数据)的条件分布密度函数。我们的目的是计算观测后验分布P(θ/Y)的参数，于是记θi为第i+1次迭代开始时后验参数的估计值，则第i+1次迭代为:

E步:将P(θ/Y，Z)或logP(θ/Y，Z)关于Z的条件分布求期望，从而把Z积掉，即

M步:将Q(θ/θi，Y)极大化，即找一个点θi+1，使

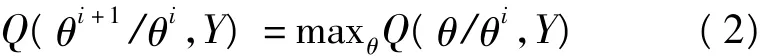
如此形成了一次迭代θi→θi+1，θi+1∈M(θi)，这里M(θi)是在整个参数空间Ω内使得Q(θi+1/θi，Y)最大的θ的值所组成的集合。将上述E步和M步进行迭代直至 θi+1-θi或者 Q(θi+1/θi，Y)-Q(θi/θi，Y)充分小时为止。

EM算法在每一次迭代后均提高观测极大似然密度函数值，具有良好的全局收敛性［8，9］。

2.2 GPS高程拟合数学模型

设GPS高程拟合数学模型为

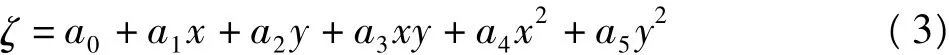
式中，ζ为高程异常，a0，a1，…，a5为拟合参数，x、y为拟合点坐标。等式右边取前三项为平面拟合法(三参数法)，取前四项为平面相关拟合法(四参数法)，取六项则为二次曲面拟合法(六参数法)。

若测区内有n(n≥6)个控制点，且经过GPS观测已知它们的高程异常，根据式(3)列出误差方程为［10］:

式中，

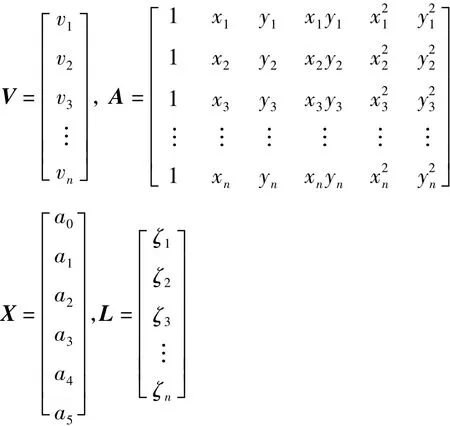
利用最小二乘原理［10，11］计算参数X的解为:

二次曲面拟合参数确定后可确定局部区域的高程异常曲面(似大地水准面)，继而推算出其他待定点的高程异常，根据GPS高程观测值计算出待定点的正常高。

2.3 缺失数据下基于EM算法的GPS高程拟合方法

由于某一区域内GPS无信号;环境恶劣水准测量无法进行;控制点被破坏或找不到等因素，造成部分重要的拟合点数据缺失，采用二次曲面拟合时将会影响高程异常曲面的准确度。当缺失数据过多时(n≤6)，导致二次曲面拟合法无法使用，仅能采用平面拟合法或平面相关拟合法;测区过大时，采用这两种方法无法保证GPS高程的测量精度。EM算法可有效解决上述问题，二次曲面拟合法的误差方程中误差向量V服从高斯正态分布，应用EM算法可建立似然函数方程P(θ/Y，Z)，

假设拟合数据ζt缺失，式中θ为待估参数(a0，a1，…，a5，σ)，Y为不完全观测数据，Z为缺失数据ζt。

误差向量V服从高斯正态分布，因此可以得到缺失数据ζt的条件分布概率密度函数为:

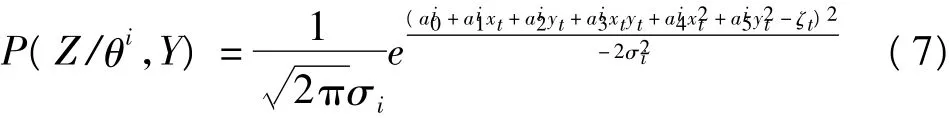
式中，θi为经过i次迭代后的参数值。由式(6)、(7)得到EM算法的期望步:

EM算法的极大化步，将Q(θ/θi，Y)极大化，积分后对各参数求偏导数，计算得到参数θi+1，将θi+1代入 E步进行迭代，循环直至 θi+1-θi或者Q(θi+1/θi，Y)-Q(θi/θi，Y)充分小时为止。

3 算例分析

以杭州湾跨海大桥的GPS高程拟合数据为例，GPS控制网点位分布见图1。

图1 GPS控制网点位略图Fig.1 GPS control points network

图1中，GP01至GP07为分布均匀的GPS控制网点，其点位坐标和高程异常均已知，可作为GPS高程拟合点使用。

现假设GP03、GP06点因观测条件限制数据缺失，拟合点仅有GP01、GP02、GP04、GP05和GP07 5个数据。由于达不到二次曲线拟合法所需拟合点n≥6的条件，因此采用平面相关拟合法。应用Matlab编程计算得平面相关拟合结果见表1。

采用EM算法进行数据处理，数学模型为二次曲面拟合模型，θ为参数(a0，a1，…，a5，σ)期望步计算GP06点的条件期望，以GP05、GP07点的高程异常值为积分区间，应用 Matlab编程迭代计算，当θi+1-θi的值小于0.000 01时停止迭代，拟合结果见表2。

完全数据下采用二次曲面拟合法，以GP01、GP02、GP04、GP05、GP06和 GP07为拟合点，计算结果与平面相关拟合法和EM算法比较结果见表3。

表1 平面相关拟合结果(单位：cm)Tab.1 Results of related plane fitting(unit：cm)

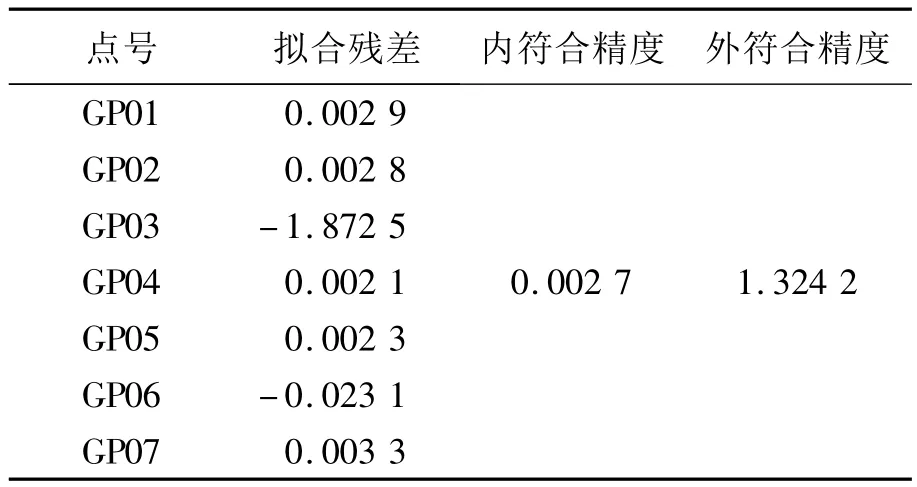
表2 EM算法拟合结果(单位：cm)Tab.2 Results from fitting with EM algorithm(unit：cm)

表3 拟合结果统计(单位：cm)Tab.3 Statistics of fitting results(unit：cm)

表3表明，在缺失数据的情况下，使用平面相关拟合法很难保证高程拟合的精度，而采用EM算法，引入了缺失数据的条件期望，有效地提高了高程拟合精度。与完全数据下的二次曲面拟合法相比较，内符合精度相差很小，外符合精度提高，表明了EM算法的有效性。

4 结论

拟合似大地水准面的精度直接影响着GPS高程测量的精度，高程拟合时拟合点分布均匀且数据充足，才能较好地拟合出似大地水准面。而在拟合点观测中难免会遇到部分重要的拟合点因观测条件限制而无法观测，造成数据缺失。采用不完全的拟合点数据拟合似大地水准面将降低似大地水准面的拟合准确度。应用EM算法，将观测数据的误差分布信息引入数据计算中，引入缺失数据的条件期望，添加了“潜在数据”，较好地改善了缺失数据下的拟合似大地水准面精度，与完全数据下的拟合相比，提高了外符合精度。因此，在缺失数据的情况下，应用EM算法进行GPS高程拟合是一种行之有效的方法。

1 孔祥元，郭际明，刘宗泉.大地测量学基础［M］.武汉:武汉大学出版社，2002.(Kong Xiangyuan，Guo Jiming and Liu Zhongquan.The base of geodesy［M］.Wuhan;Wuhan University Press，2002)

2 魏立峰，何建国.GPS高程拟合似大地水准面的方法［J］.地理空间信息，2010，8(4):72-76.(Wei Lifeng and He Jianguo.Methods for GPS height fitting quasi-geoid［J］.Geospatial Information，2010，8(4):72-76)

3 姚吉利，曲国庆，刘科利.拟合点分布与GPS水准面拟合精度关系研究［J］.大地测量与地球动力学，2008，(5): 50-54.(Yao Jili，Qu Guoqing and Liu Keli.Research on accuracy of quasi-geoid with fitting methods under different distribution of GPS points［J］.Journal of Geodesy and Geodynamics，2008，(5):50-54)

4 姚喜，栾学科，王志博.GPS水准拟合方法的研究［J］.测绘科学，2010，35:42-43.(Yao Xi，Luan Xueke and Wang Zhibo.Research on GPS level fitting methods［J］.Science of Surveying and Mapping，2010，35:42-43)

5 曾传璜，等.EM算法的研究［J］.软件导刊，2008，7(9): 97-98.(Zeng Chuanhuang，et al.Research of EM algorithm［J］.Software Guide，2008，7(9):97-98)

6 Dempster A P，Laird N M and Rubin D B.Maximum likelihood from incomplete data via the EM algorithm［J］.Journal of the Royal Statistifcal Society B，1977，39:1-38.

7 钱俊，舒宁.基于EM算法和单幅雷达图像阴影的控制点坡度校正［J］.武汉大学学报(信息科学版)，2004，29 (12):1 089-1 092.(Qian Jun and Shu Ning.Correction of control point slope based on EM algorithm and shading of single SAR image［J］.Geomatics and Information Science of Wuhan University，2004，29(12):1 089-1 092)

8 Graham C G and Juan C A.Approximate EM algorithms for parameter and state estimation in nonlinear stochastic models［A］.Proceedings of the 44th IEEE conference on decision and control，and the European Control Conference［C］.2005，12-15.

9 王兆军.EM算法收敛的必要条件［J］.南开大学学报(自然科学版)，1994，(2):85-88.(Wang Zhaojun.The necessary condition on the convergence of the EM algorithm［J］.Acta Scientiarum Naturalium Universitatis Nankaiensis，1994，(2):85-88)

10 武汉大学测绘学院测量平差学科组.误差理论与测量平差基础［M］.武汉:武汉大学出版社，2003.(Research group of Surveying Adjustment，School of Surveying and Mapping，Wuhan University.The base of errors theory and surveying adjustment［M］.Wuhan;Wuhan University Press，2003)

11 杨元喜，张丽萍.中国大地测量数据处理60年重要进展［J］.地理空间信息，2010，8(1):1-6.(Yang Yuanxi and Zhang Liping.Progress of geodetic data processing for 60 years in China［J］.Geospatial Information，2010，8 (1):1-6)

GPS ELEVATION FITTING BASED ON EM ALGORITHM FOR LACK OF DATA

Lin Dongfang，Song Yingchun，Du Kun and Xiao Qinqin
(School of Geosciences and Info-Physics，Central South University，Changsha 410083)

Restricted by the observing conditions，some important data of GPS elevation fitting are often missed or not enough.Using conventional methods will reduce the fitting accuracy of the quasi-geoid.By use of the EM algorithm with the addition of“potential data”，conditional expectation of the missing data，it can effectively improve the accuracy of GPS elevation fitting for lack of data.

missing data;EM algorithm;elevation fitting;related plane fitting;quadratic surface fitting

1671-5942(2012)02-0139-04

2011-11-12

国家自然科学基金(40874005);教育部博士点基金(200805331086)

林东方，男，1986年生，硕士研究生，主要研究方向为:现代测量数据处理.E-mail:lindongfang223@163.com

P207

A