LCRⅡ型和Ⅰ型航空重力仪的同机飞行试验*
孙中苗 翟振和 李迎春 肖 云
(西安测绘研究所,西安 710054)
LCRⅡ型和Ⅰ型航空重力仪的同机飞行试验*
孙中苗 翟振和 李迎春 肖 云
(西安测绘研究所,西安 710054)
为检验和评价LCRⅡ型航空重力仪的精度和性能,与LCRⅠ型航空重力仪进行了同机飞行试验。试验结果表明,Ⅱ型与Ⅰ型航空重力仪相比,采样点重力异常之差值的标准差为4.0×10-5ms-2,单套重力仪的测量精度约为2.8×10-5ms-2;5'×5'格网平均重力异常之差的标准差为4.9×10-5ms-2,每套系统获得的5'×5'格网平均重力异常的精度为3.5×10-5ms-2,剔除两个可疑值后,精度为2.9×10-5ms-2。总体上,LCRⅡ型航空重力仪与Ⅰ型精度相当,但具有更快的仪器稳定速度。
航空重力测量;航空重力仪;重力异常;低通滤波器;同机飞行
1 引言
顾名思义,航空重力测量是利用航空重力仪(或其他加速度计)在空中测量地球重力场信息的一种重力测量方法。2002年,我国首套航空重力测量系统(CHAGS)正式投入使用[1],迄今已取得较为满意的成果[2-4]。首套CHAGS的重力传感器分系统采用美国LaCosteamp;Romberg公司的S/A型(Ⅰ型)海空重力仪。该公司在2002年对I型海空重力仪的控制系统部分进行了较大幅度的全数字化改进,主要包括:1)采用Microsoft Windows界面取代DOS界面;2)控制柜和传感器一体化的紧凑设计; 3)可输入GPS时间;4)采用内部高精度铷钟进行时间同步;5)所有需用手工调整的程序简化为通过软件用户界面进行调整;6)设备配置操作更加简单; 7)采用用户可调的FIR低通滤波器,代替原来的IIR低通滤波器;8)开机自动检测、校准;9)自动记录内外温度、气压等环境参数。改进后的系统即“海空重力系统II”(LCRⅡ)具有界面友好、更紧凑、能自包含等优点,但其核心部件即重力传感器和陀螺稳定平台未加改进。
在第二套CHAGS中,我们采用了LCRⅡ型航空重力仪。为检验和评价该新型设备的精度和性能,2007年8月在某中等山区与LCRⅠ型航空重力仪(其精度和性能已经过多次试验验证)进行了同机飞行试验。本文将介绍同机试验的有关情况,并对两套重力仪的精度进行详细比较和分析。
2 数据处理方法概述
2.1 数据处理模型
航空重力测量采用相对重力测量原理,在飞机起飞前、降落后航空重力仪需作静态观测,以将重力观测值与停机坪的重力基准值相联系。航空重力标量测量的基本数学模型为[2,5]:
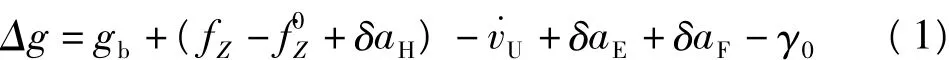
式中,Δg表示测线采样点的重力异常;gb系停机坪处的重力基准值;fZ为比力及其初值;˙vU为飞机垂直加速度;δaE为厄特弗斯改正;δaH为水平加速度改正;δaF系空间改正;γ0系正常重力。
比力fZ的计算公式为:
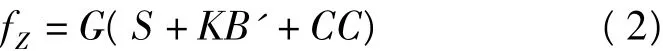
式中,G为格值,用于将重力计数单位转换成毫伽单位;S为弹簧张力;K为摆杆尺度因子,即K因子;B'为摆杆速度,可由摆杆位置差分求得;CC为交叉耦合改正。
对于第一套系统,交叉耦合改正CC在重力仪中有直接输出;而LCRⅡ型航空重力仪中没有直接输出,需要由交叉耦合的5个线性监视项按下式计算得到[6,7]。
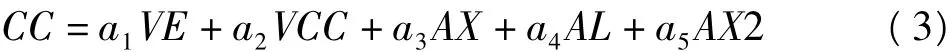
式中,VE、VCC、AX、AL、AX2分别是5个CC监视项的名称,ai(i=1,…,5)为CC系数。
式(1)中除停机坪处的重力基准值gb外,(fZ-+δaH)需由重力仪观测值计算得到,而其余各项均由GPS数据算得。显然,若采用相同的GPS数据,(fZ-+δaH)实质上反映了重力仪的不同。此外,受大气湍流和飞机长周期运动等因素影响,由式(1)直接求得的重力异常中含有大量高频噪声,因此,需进行低通滤波处理以将测量噪声降低至可以接受的水平。
2.2 低通滤波器设计
低通滤波器的主要作用是减弱或消除航空重力测量观测值中的高频噪声。飞机垂直加速度一般可以达到0.5 ms-2(RMS),峰值有时高达几ms-2。对低湍流情况,未滤波重力异常的RMS值为0.02~0.05 ms-2;对于高湍流RMS可达0.2 ms-2,故噪声完全淹没了实际的重力异常信号。但由于这些噪声通常表现为高频特性,故采用低通滤波器可以有效地消除或减弱其影响。
低通滤波器的设计与应用需兼顾待求重力异常的空间分辨率和精度。短周期的低通滤波器有利于提高空间分辨率,但难以保证精度,反之亦然。无限冲激响应滤波器(IIR滤波器,如RC滤波器、巴特沃思滤波器)和有限冲激响应(FIR)滤波器是航空重力测量中常用的两类低通滤波器。按照空中原始重力异常的频谱特性以及分辨率和精度要求,我们自行设计了级联式巴特沃思滤波器[2],其幅频响应示于图1。低通滤波器的截止频率为0.003 3 Hz,相应的时域周期为300 s,当飞机飞行速度为250 km/h时,对应的半波长分辨率约为10 km。
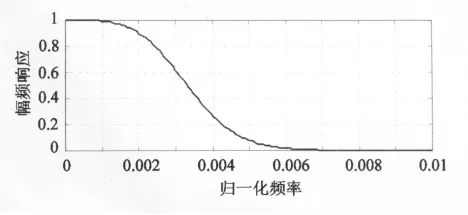
图1 级联式巴特沃思滤波器的幅频响应Fig.1 Amplitude response of the cascade Butterworth filter
3 试验结果与分析
3.1 试验概况
试验区域属于中等山区,最高海拔2 100多米。试验分为两种情况,一是搭载试验,在第一套航空重力测量系统作业时搭载LCR II型航空重力仪,即两套重力仪同机试验;二是第二套航空重力测量系统的单独试验。
试验运载平台为某型航测机,测量期间的平均飞行速度为250 km/h,飞行高度为2 800 m。在飞行区域内布设了3个GPS地面观测站,飞机上安装了2个GPS动态天线,实现飞机的动态差分定位。测量一般于每天的8:00~18:00进行,测量条件属于中等湍流条件。
为便于比较,以下仅给出同机搭载试验情况。搭载试验测线数为18条,其中南北12条,东西6条。搭载试验时GPS观测数据完全相同,不同的是航空重力仪的观测数据。LCRⅡ型航空重力仪的精度按如下三种方法进行分析和比较,一是以各采样点的重力异常之差;二是以5'×5'格网平均重力异常之差;三是以各自交叉点不符值。
3.2 采样点的重力异常之差
利用相同的GPS观测数据和第一、第二套航空重力仪观测数据,可以分别求得各条测线每个采样点的重力异常。采样点的重力异常之差反映了两套航空重力仪的差异。不失一般性,我们选择了飞行测量条件较好的10条测线进行了比较。10条测线的重力异常的互差统计于表1。

表1 采样点的重力异常之差统计(单位:10-5ms-2)Tab.1 Differences of the gravity anomaly for the sample points(unit:10-5ms-2)
从表1可以看出,采用相同的GPS数据,由两套航空重力仪观测数据计算得到的采样点的重力异常非常吻合,其差值的标准差为4.0×10-5ms-2。顾及两套重力仪的观测值互为独立,并假设两套航空重力仪的观测精度相当,则每套重力仪的测量精度约为2.8×10-5ms-2。
应当指出的是,上述的航空重力仪观测值尚包含了水平加速度改正的影响,因此与纯粹的航空重力仪观测值在概念上是有所区别的。也就是说,重力异常互差的标准差中还包括了水平加速度改正误差的影响。
3.3 格网平均重力异常之差
航空重力测量的最终产品通常是格网平均重力异常,为此我们将测线重力异常构成空中5'×5'格网平均重力异常,以此比较两套重力仪的精度。此处,我们构成了107个5'×5'格网平均重力异常。图2示出了格网平均重力异常之差,图2中符号‘×’表示差值为负值,符号‘×’表示差值为正值,各符号的大小反映了差值的大小,差值统计于表2。
由表2可见,107个5'×5'格网平均重力异常之差的标准差为4.9×10-5ms-2。现仍假设两套航空重力仪的观测精度相当,则由每套系统获得的5'× 5'格网平均重力异常的精度为3.5×10-5ms-2。由图2可见,差值中有两个可疑值,将其剔除后,精度为2.9×10-5ms-2。
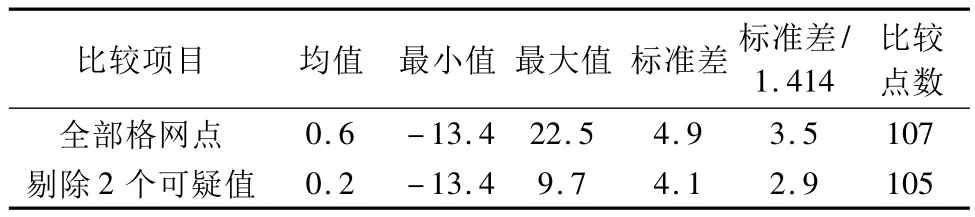
表2 5'×5'格网平均重力异常之差统计(单位:10-5ms-2) Tab.2 Differences of the mean gravity anomaly for 5'×5'grid(unit:10-5ms-2)
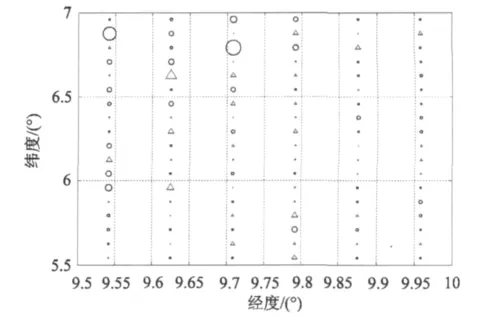
图2 5'×5'格网平均重力异常之差Fig.2 Differences of the mean gravity anomaly for 5'×5' grid
3.4 交叉点不符值
利用两套系统各自的交叉点不符值,能够大致评价两套系统的性能。对于搭载试验的18条测线,可以构成58个交叉点。表3是交叉点不符值的统计结果。

表3 交叉点不符值统计(单位:10-5ms-2)Tab.3 Statistics of crossover errors(unit:10-5ms-2)
从表3可知,第一套系统的交叉点不符值要比第二套系统的大些,这具体反映在标准差上。但利用抗差估计[8],即根据交叉点不符值的大小赋以不同权系数后,两者的标准差趋于一致。交叉点平差后,精度有所提高。总体而言,第二套系统的精度略优于第一套系统。
此外,从作业过程以及数据处理过程中我们发现,第二套航空重力仪要比第一套稳定得快,即在相同的作业时间内,第二套系统的有效观测数要多些。图3示出了测线NS308的相关情况,显然第一套系统的两端数据难以接受。
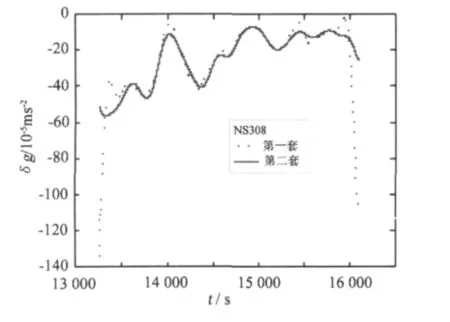
图3 两套重力仪稳定速度的比较Fig.3 Comparison of the stable time for the LCR gravimeterⅡandⅠ
4 结论
1)基于相同的GPS数据,由两套航空重力仪观测数据计算得到的采样点的重力异常非常吻合,其差值的标准差为4.0×10-5ms-2。顾及两套重力仪的观测值互为独立,并假设两套航空重力仪的观测精度相当,则每套重力仪的测量精度约为2.8× 10-5ms-2。
2)采用同样的GPS数据,107个5'×5'格网平均重力异常之差的标准差为4.9×10-5ms-2,每套系统获得的5'×5'格网平均重力异常的精度为3.5 ×10-5ms-2,剔除两个可疑值后,精度为2.9×10-5ms-2。
3)对于同样的交叉测线,第一套系统的交叉点不符值的标准差要比第二套系统的相应值大些。抗差估计后,两者趋于一致。第二套系统的总体精度略优于第一套系统,且第二套航空重力仪的稳定时间比第一套稍短,即在相同的作业时间内,第二套系统可获得更多的有效观测。
1 夏哲仁,等.航空重力测量系统(CHAGS)[J].测绘学报,2004,33(3):216-220.(Xia Zheren,et al.Chinese Airborne Gravimetry System(CHAGS)[J].Acta Geodaetica et Cartographica Sinica,2004,33(3):216-220)
2 孙中苗.航空重力测量理论、方法及应用研究[D].郑州:信息工程大学.2004.(Sun Zhongmiao.Theory,methods and applications of airborne gravimetry[D].Zhengzhou:Information Engineering University.2004)
3 孙中苗,等.平原地区航空重力测量的精度分析[J].测绘通报,2006,10:1-4.(Sun Zhongmiao,et al.Accuracy evaluation of airborne gravimetry over plain area[J].Bulletin of Surveying and Mapping,2006,10:1-4)
4 夏哲仁,等.航空重力测量系统试验报告[J].测绘科学与工程,2005,25(1):6-10.(Xia Zheren,et al.Test report of the Chinese airborne gravimetry system[J].Geomatic Science and Engineering,2005,25(1):6-10)
5 Schwarz K P and Li Y C.An introduction to airborne gravimetry and its boundary value problems[M].Como Italy: Lecture Notes of IAG International Summer School,1996: 312-322.
6 Vallioant H D.The LaCoste and Romberg air/sea gravity meter:an overview[M].CRC Handbook of Geophysical Exploration at Sea,2nd edition,1991:159-165.
7 孙中苗,夏哲仁,李迎春.LaCosteamp;Romberg航空重力仪的交叉耦合改正[J].武汉大学学报(信息科学版),2006,31(10):883-886.(Sun Zhongmiao,Xia Zheren and Li Yingchun. Cross-coupling correction for LaCosteamp;Romberg airborne gravimeter[J].Geomatics and Information Science of Wuhan University,2006,31(10): 883-886)
8 Yang,Y.Robust estimation for dependent observations[J].Manuscripta Geodaetica,1994,19:10-17.
CONCURRENT FLIGHT TEST OF LaCosteamp;Romberg(LCR) AIRBORNE GRAVIMETERⅡANDⅠSYSTEM
Sun Zhongmiao,Zhai Zhenhe,Li Yingchun and Xiao Yun
(Xi’an Research Institute of Surveying and Mapping,Xi’an 710054)
In order to validate the accuracy and the performance of the LaCosteamp;Romberg(LCRⅡ),a concurrent flight test over a mountain area was undertaken.The LCR gravimeterⅡand an LCR gravimeterⅠsystem side by side.The results of the flight test show that the standard deviation of the gravity anomalies difference measured with the two systems is about 4.0×10-5ms-2namely the accuracy of the single system is about 2.8×10-5ms-2if we assumed the two systems have the same accuracy.They also indicate that the standard deviation of the 5' ×5'grid mean gravity anomalies difference from the two systems is about 4.9×10-5ms-2namely the related accuracy of the single system is about 3.5×10-5ms-2and 2.9×10-5ms-2after two outliers were eliminated.In general,LCR gravimeterⅡsystem has the identical accuracy as the LCR gravimeterⅠsystem,but it can be quickly leveling off.
airborne gravimetry;airborne gravimeter;gravity anomaly;lowpass filter;concurrent flight
1671-5942(2012)02-0024-04
2011-12-27
国家自然科学基金(41174017)
孙中苗,男,1968年生,研究员,博导,博士。现从事航空重力测量理论与方法研究.E-mail:sun_szm@sina.com
P223+.4
A

