航空重力测量测线网平差中的粗差处理*

周波阳 罗志才 林 旭 周 浩

(1)武汉大学测绘学院，武汉 430079

2)武汉大学地球空间环境与大地测量教育部重点实验室，武汉430079)

航空重力测量测线网平差中的粗差处理*

周波阳1)罗志才1，2)林 旭1)周 浩1)

(1)武汉大学测绘学院，武汉 430079

2)武汉大学地球空间环境与大地测量教育部重点实验室，武汉430079)

航空重力测量测线网平差的主要任务是进行系统误差的补偿。为了削弱粗差观测值的影响，提高补偿效果，引入阈值法和抗差估计，并采用模拟数据验证了这两种方法的有效性和可靠性。通过比较发现，抗差估计在航空重力测线网平差中具有更好的实用价值。

航空重力测量;测线网平差;阈值法;抗差估计;权函数

1 引言

在航空重力测量中，为了尽可能地构成重复观测，正确评价测量精度，测线往往布设成交叉网状，在交叉点处两条测线上的重力值理论上应该是相等的，但由于测量平台在高空作业，处于不断高速的运动状态，观测环境较为复杂，各类观测值不可避免地受到“污染”，从而导致观测值在交叉点处存在不符值。采用低通数字滤波等技术消除高频噪声后，观测值中仍存在各种误差源的干扰和影响。这些干扰和影响按其表现形式可分为偶然误差、系统误差以及粗差。偶然误差的原因十分复杂，空气扰动、机器零件的摩擦、气压、气温的变化等，以及它们的综合影响均能产生;系统误差主要由厄特弗斯效应、姿态误差、卫星星历误差等引起;GPS、加速度计等的工作状态反生异常时观测值中容易出现粗差。

航空重力测量测线网平差中的粗差处理通常和系统误差的补偿同步进行，忽略粗差直接采用最小二乘来估计系统误差模型参数时，所建立的误差模型并不能真实反映系统误差的变化规律。平差后，大粗差的影响也会被分配到许多正常观测值上，从而扭曲平差结果，参数估值的效率和可靠性就会受到严重的损害［1］。有效地消除或削弱观测数据中粗差对于参数估值的不良影响，是提高航空重力测量网平差精度的关键环节。一般来说，对粗差的处理方式主要有3类:第一类即计算机辅助图形可视化法，通过人机交互的方式来实现粗差的探测和剔除。当前数据处理都趋于自动化，人为干预排除粗差的方式将被淘汰［2］;第二类是在平差前采用某些方法对粗差定位并剔除，Dixon准则［3］、Grubbs准则［3］、χ2检验［4］、τ标准检验［4］、F检验［5］、t检验［6］、小波分析方法［3，7］以及阈值法［3］可以对粗差定位。其中Dixon准则无需估算样本均值、样本标准差和残余误差，在将所有观测值按照从小到大的顺序排列后，Dixon准则认为粗差观测值仅存在于重排序之后的数据两端。Dixon准则仅适合于小样本(3＜n＜30)，采用Dixon准则进行小样本数据的粗差探测能够得到较严密的结果［8］。Grubbs检验、F检验等统计检验法都派生于最小二乘估计，对于偏离正态分布的数据是不可靠的，它们几乎不可能把剔除粗差与估计量的计算分开，利用不可靠的估计量来进行统计检验就很难保证这种统计检验方法的正确性［2］。小波分析方法实质上是对观测值信号进行滤波，利用小波变换的高低频分离的特点，可在不丢失原始信号重要信息成分的前提下，对信号进行放大并对其进行特征提取，它也是一种较为有效的粗差探测方法，但算法较为复杂。阈值法计算方便简单，适用于观测数据的快速粗差探测;第三类则是基于多维M估计建立参数模型的抗差解式，采用等价权思想将其转化为最小二乘解形式［9］。采用迭代的抗差M估计，既保留了最小二乘法的优越性，又保证被估参数既能抵制模型误差又能抗拒粗差的影响［1，10］。本文将抗差M估计和阈值法应用于航空重力测量测线网平差中的粗差处理，并通过模拟计算对这两种方法进行评价。

2 系统误差补偿的两步法

航空重力测量的测线网平差实际上是系统误差的补偿问题，进行系统误差补偿的一般方法为自检校测线网平差法，但自检校平差会导致法方程奇异，为了解决这个问题，将自检校测线网平差过程进行简化，将误差理论模型简化为实用模型，即为误差补偿的两步法［11-13］。

2.1 交叉点平差

第一阶段使用条件平差法对测线交叉点进行平差。在主测线、副测线的交叉点处可建立如下的误差方程:

式中，Δgik与Δgjk分别为主测线i、副测线j在交叉点k处的重力异常，Δgik-Δgjk表示交叉点不符值，Vik、Vjk为改正数。对于具有多个交叉点的测线网，可以写出交叉点条件方程的矩阵形式为

其中，V由每一条测线上交叉点处的改正数组成，系数阵B是由1、-1和大量的0构成，W为交叉点不符值。依据最小二乘平差理论可解得

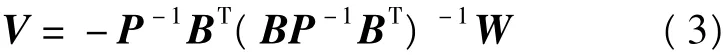
一般来说，测线上各个测点为独立等精度观测，权阵P为单位阵。

2.2 测线系统误差估计

以观测时间t为自变量，以式得到的交叉点不符值的改正数V为虚拟观测值，遍历所有测线对每个交叉点建立如下形式的误差方程

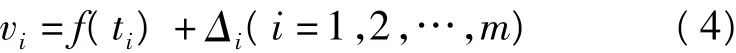
vi为V中的第i个元素，f(t)为系统误差模型，Δi为噪声，m为该测线上的交叉点个数。f(t)有如下两种形式:

1)一般多项式模型

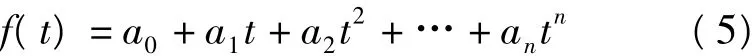
2)三角多项式形式

则误差方程的矩阵形式为

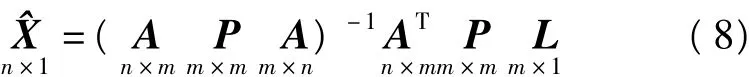
3 粗差处理方法

3.1 阈值法

Huber［2］在1977年采用Tukey污染分布模拟了一些含有不同数量粗差的正态分布数据，其污染正态分布模式为

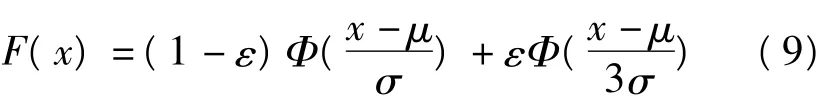
其中Φ是标准正态分布，ε为污染率，是一小量，μ和σ分别为母体均值和标准差。式(9)表明，与均值之差的绝对值大于3σ的观测值被认为是粗差。而实际观测中，被测量的真实值大多是未知，μ和σ不能精确知道，通常以样本均值和标准差S代替。阈值法的实用形式为

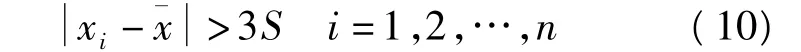
在实际操作过程中，把交叉点平差后的不符值的改正数V作为观测值向量X，当观测值xi(xi实际上为交叉点不符值的改正数vi)满足式(10)时，被认作是粗差。

3.2 抗差M估计

经典最小二乘估计是利用一组来自于母体为正态分布的观测值，求定母体参数的一种参数估计，它的最优统计特性(不能脱离观测值母体)是正态分布，即观测值中仅含有偶然误差这一前提［14］。因此，最小二乘估计对偏离正态分布的数据是不可靠的。与最小二乘估计相比，抗差估计应具备两大特点:一是它能消除和削弱粗差对估值的影响;二是它基本上具备经典估计的优良特性。

按M估计原理，取极值函数为

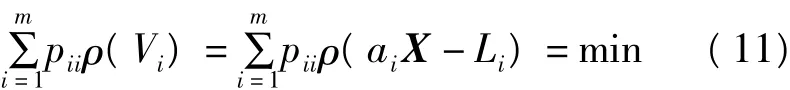
其中，ai为系数阵A的第i行。对X求导，并令其为0，同时记φ(Vi)=∂ρ/∂Vi，则有

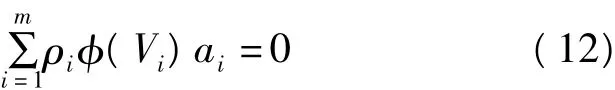
令φ(Vi)/Vi=Wi(权因子)=piiWi为等价权元素，则式(12)可写为

由此，可得到抗差M估值

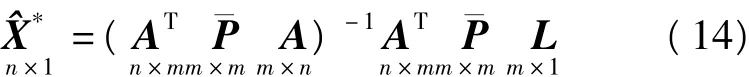
抗差估计采用迭代解法，每一次迭代相当于进行一次最小二乘估计，但应以等价权代替先验权。式(7)的第k+1步迭代解为

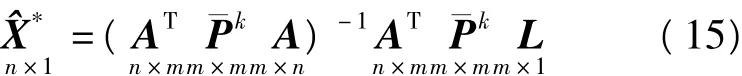
抗差估计的结果取决于所选取的等价权函数，权函数不一样，抗差估计的模型就不同，抗差的效果也不一样［15］。常见的等价权模型有Huber权函数、Hampel权函数、Tukey权函数和 Andrews权函数等［9］。本文仅以Huber等价权模型为例进行了抗差估计，其具体形式为:

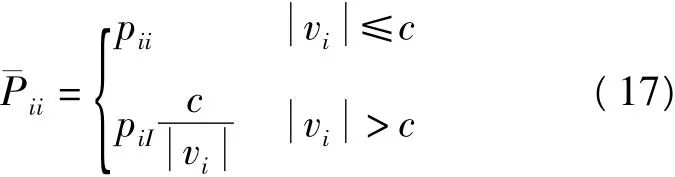
式中c一般取2.0。

4 算例及结果分析

本文模拟了某航空重力测区，它由10条横向测线和10条纵向测线组成，飞机起伏飞行，飞行时离地面高度约为1.8 km。应用两步处理法对观测数据进行处理，第一阶段交叉点平差后主、副测线验后单位权中误差见表1～2。为了更好地检验阈值法和抗差M估计的实际效果，在这些交叉点不符值的改正数中随机挑选10个加入绝对值分别为(10～18)×10-5ms-2和(6～10)×10-5ms-2的粗差，形成两组观测值data1和data2，其交叉点的分布如图1。在两步处理法第二阶段中分别采用阈值法和抗差估计来消除粗差的影响，系统误差模型为2阶和3阶一般多项式，表3～9给出了相应的最小二乘估计(LSE)和抗差估计(RE)结果。

图1 交叉点的分布Fig.1 Distribution of crosspoints

由表1可见，用阈值法进行粗差的剔除后，数据的标准偏差变小，测线网精度有所提高。这说明阈值法能有效对粗差进行识别和定位，是一种可靠的粗差探测手段，但它的缺点也很明显，其对绝对值较小的粗差不敏感，且在剔除粗差观测值之后，会导致交叉点个数变少，这将给后续研究带来不利影响。

从表4～7可以看出，当部分观测值含有粗差时，主、副测线的最小二乘估计验后单位权中误差均大于抗差估计验后单位权中误差，这说明当观测值含有粗差时，从整体精度上，采用抗差估计进行系统误差补偿的成果明显优于采用最小二乘估计进行系统误差补偿的成果。但我们也不能单纯的以交叉点不符值的均方差大小作为衡量抗差效果唯一标准。当信噪比一定时，计算结果很大程度上取决于误差模型的合理选择，从本算例来看，二阶多项式的抗差效果更好。反之，当系统误差模型一定时，信噪比越低，观测值含粗差的绝对值较大时，抗差效果越明显。

表1 不含粗差时主测线系统误差模型验后单位权中误差(单位：10-5ms-2)Tab.1 Posteriori unit weight mean errors of system error model on main line of data without outliers(unit：10-5ms-2)

表2 不含粗差时副测线系统误差模型验后单位权中误差(单位：10-5ms-2)Tab.2 Posteriori unit weight mean errors of system error model on vice line of data without outliers(unit：10-5ms-2)

表3 阈值法处理结果(单位：10-5ms-2)Tab.3 Results of Thresholding method(unit：10-5ms-2)

表4 data1主测线系统误差模型参数验后单位权中误差(单位：10-5ms-2)Tab.4 Posteriori unit weight mean errors of system error model on main line of data1(unit：10-5ms-2)

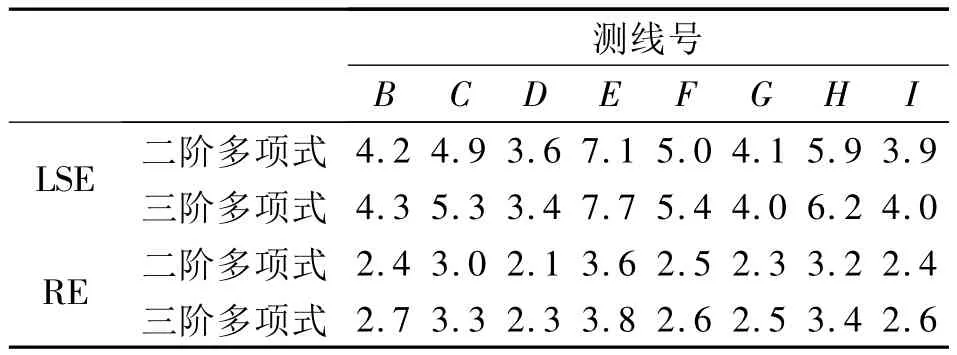
表5 data1副测线系统误差模型参数验后单位权中误差(单位：10-5ms-2)Tab.5 Posteriori unit weight mean errors of system error model on vice line of data1(unit：10-5ms-2)

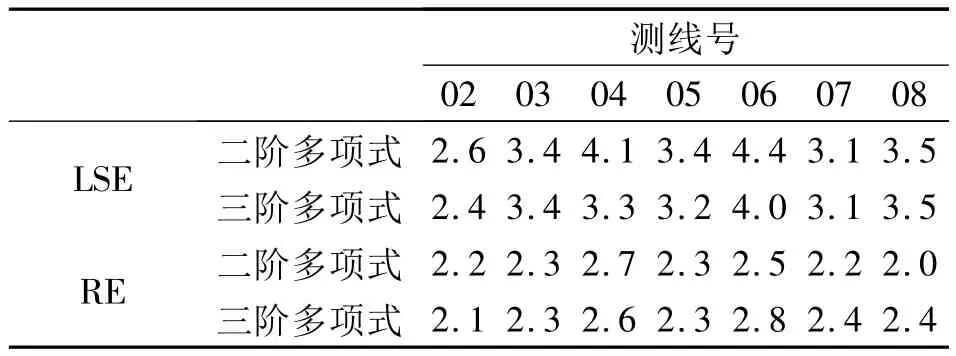
表6 data2主测线系统误差模型参数验后单位权中误差(单位：10-5ms-2)Tab.6 Posteriori unit weight mean errors of system error model on main line of data2(unit：10-5ms-2)

表7 data2副测线系统误差模型参数验后单位权中误差(单位：10-5ms-2)Tab.7 Posteriori unit weight mean errors of system error model on deputy line of data2(unit：10-5ms-2)

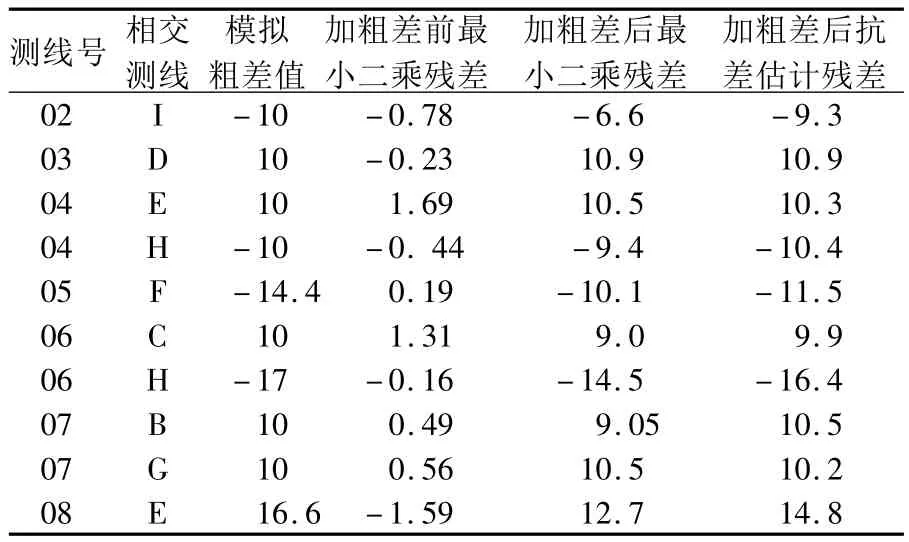
表8 data1交叉点最小二乘残差与抗差估计残差(单位：10-5ms-2)Tab.8 Residuals of least squares estimation and robust estimation of data1(unit：10-5ms-2)

表9 data2交叉点最小二乘残差与抗差估计残差(单位：10-5ms-2)Tab.9 Residuals of least squares estimation and robust estimation of data2(unit：10-5ms-2)

表8～9列出了不含粗差时最小二乘残差、加粗差后最小二乘残差以及加粗差后抗差M估计的残差(系统误差模型为二阶多项式)。不难发现，加粗差后抗差M估计的残差比最小二乘估计的残差更接近于粗差值本身，在异常观测值上抗差M估计具有明显的抵御粗差干扰的能力，这是因为在迭代计算时，抗差M估计利用等价权模型对异常观测值实施了降权操作。通过对残差进行分析对比，抗差估计不仅能对粗差的位置进行识别，而且还能对粗差的大小进行估计。上述结果还表明，当粗差绝对值较小时，抗差估计仍然能够对其进行识别和定位。从这方面来讲，抗差估计比阈值法更加有效和可靠。

5 结语

对于各测线上的所有采样点的系统误差补偿来说，阈值法和抗差估计均具有一定的抗差效果。阈值法是直接剔除异常观测值，而抗差M估计能在拒绝和接受一个观测值之间起一个平滑的作用。相比较而言，抗差估计可靠性更高，更加有效。值得注意的是，任何一种抗差估计方法的实际抗差能力都是有一定条件的，当粗差个数过多、绝对值较小时，阈值法和抗差估计对粗差的处理结果往往不够理想。后续研究将考虑更加复杂的系统误差模型(如三角多项式)和更为丰富的权函数模型以及对系统误差模型的参数进行显著性检验。

1 杨元喜.抗差估计理论及其应用［M］.北京:八一出版社，1993.(Yang Yuanxi.Theory of robust estimation and its application［M］.Beijing:Bayi Press，1993)

2 黄幼才.数据探测与抗差估计［M］.北京:测绘出版社，1990.(Huang Youcai.Data detection and robust estimation［M］.Beijing:Mapping Press，1993)

3 Kern M，et al.Outlier detection algorithms and their performance in GOCE gravity field Processing［J］.Journal of Geodesy，2005，78(9):509-519.

4 Hwang C，Wang C G and Lee L H.Adjustment of relative gravity measurements using weighted and datum-free constraints［J］.Computeramp;Geoscience，2002，28:1 005-1 015.

5 李德仁.误差处理和可靠性理论［M］.北京:测绘出版社，1988.(Li Deren.Error processing and theory of reliablity［M］.Beijing:Mapping Press，1988)

6 丁士俊，陶本藻.半参数模型的统计诊断量与粗差检验［J］.大地测量与地球动力学，2005，(3):24-28.(Ding Shijun and Tao Benzao.Measures of statistical diagnosis and gross test［J］.Journal of Geodesy and Geodynamics，2005，(3):24-28)

7 Wang Y.Jump and sharp cusp detection by wavelets［J］.Biometrika，1995，82(2):385-397.

8 杨茂兴.小样本容量测量数据中粗差的剔除［J］.计量与测试技术，2005，(1):27-28.(Yang Maoxing.The coarse error eliminating in small sample space［J］.Metrology and Measurement Technique，2005(1):27-28)

9 杨元喜.参数平差模型的抗差最小二乘解［J］.测绘通报，1994，(6):33-35.(Yang Yuanxi.Robust estimation solutions of parameter adjustment model［J］.Bulletin of Surveying and Mapping，1994，(6):33-35)

10 周江文.经典误差理论与抗差估计［J］.测绘学报，1989，18(2):115-120.(Zhou Jiangwen.Classical theory of error and robust estimation［J］.Acta Geodaetica et Carto graphica Sinica，1989，18(2):115-120)

11 黄谟涛，等.海洋重力测量系统误差补偿的两步处理法［J］.武汉大学学报(信息科学版)，2002，27(3):251 -255.(Huang Motao，et al.Two-step processing for compensating the systemic errors in marine gravity measurements［J］.Geomatics and Information Science of Wuhan University，2002，27(3):251-255)

12 李海.航空重力测量测线网平差的理论与方法［D］.解放军信息工程大学，2002.(Li Hai.Theory and methods of network adjustment of airborne gravimetry［D］.The PLA Information Engineering University，2002)

13 蔡劭琨.航空重力测量网络平差方法研究［D］.国防科学技术大学，2009.(Cai Shaokun.Research on the network adjustment of airborne gravimetry［D］.National University of Defense Technology，2009)

14 余学详，吕伟才.抗差估计在粗差探测和平差计算中的运用［J］.测绘工程，1998，8(3):40-44.(Yu Xuexiang and Lv Weicai.The application of robust estimation to the gross error detection and adjustment caculation［J］.Engineering of Surveying and Mapping，1998，8(3):40-44)

15 余学祥，吕伟才.基于标准化的相关观测抗差估计模型［J］.武汉测绘科技大学学报，1999，24(1):72-78.(Yu Xuexiang and Lü Weicai.Robust estimation model for correlated observations based on standardized residuals［J］.Journal of Wuhan Technical University of Surveying and Mapping，1999，24(1):72-78)

PROCESSING METHODS FOR OUTLIERS IN NETWORK ADJUSTMENT OF AIRBORNE GRAVIMETRY

Zhou Boyang1)，Luo Zhicai1，2)，Lin Xu1)and Zhou Hao1)

(1)School of Geodesy and Geomatics，Wuhan University，Wuhan 430079
2)Key Laboratory of Geospace Environment and Geodesy，Wuhan University，Wuhan 430079)

The main task of network adjustment of airborne gravimetry is to compensate systemic errors.In order to weaken the influence of outliers and improve the effect of compensation，this paper brings in thresholding and robust estimation，and confirms these two methods’validity and reliability in simulated data processing.By means of comparison，a conclusion is reached that the robust estimation has more practical value in the network adjustment of airborne gravimetry.

airborne gravimetry;network adjustment;thresholding;robust estimation;weight function

1671-5942(2012)02-0110-05

2011-12-25

国家自然科学基金(41174062);中国博士后科学基金(20110491189);中央高校基本科研业务费专项资金(111110)

周波阳，1983年生，博士研究生，目前从事航空重力测量数据处理研究.E-mail:byzhou@whu.edu.cn

P207

A