ALOS PALSAR雷达影像InSAR数据处理中的基线和地形误差分析*

沈 强 乔学军 金银龙 汪汉胜 江利明

(1)中国科学院测量与地球物理研究所大地测量与地球动力学国家重点实验室，武汉 430077 2)中国地震局地震研究所，武汉 430071 3)武汉大学水资源与水电工程科学国家重点实验室，武汉430072)

ALOS PALSAR雷达影像InSAR数据处理中的基线和地形误差分析*

沈 强1)乔学军2)金银龙3)汪汉胜1)江利明1)

(1)中国科学院测量与地球物理研究所大地测量与地球动力学国家重点实验室，武汉 430077 2)中国地震局地震研究所，武汉 430071 3)武汉大学水资源与水电工程科学国家重点实验室，武汉430072)

从理论上分析了InSAR处理中的两大误差源——基线和地形对形变测量精度的影响，并建立了评价模型。在此基础上，研究了上述两种误差源对ALOS PALSAR的影响，获取了两种误差对形变影响的空间分布特征。结果表明，ALOS PALSAR的轨道精度为3～5 m，在现有的轨道精度情况下，形变测量精度较差，需对基线误差进行纠正;地形误差的影响很小，主要误差源于轨道误差。在现有DEM精度条件下(SRTM DEM)，利用ALOS PALSAR，要获得优于1cm的形变测量精度，基线长度最好小于400 m。

ALOS PALSAR;InSAR;基线误差;地形误差;基线长

1 引言

InSAR技术成像特点使得该技术在地壳形变(如地震，火山运动)监测中具有独特优势，其在卫星视线向(Line Of Sight:LOS)的形变测量精度可高达3～10 mm［1，2］。但在形变测量应用中，其结果的精度仍受到诸多因素的影响。这些因素主要包括卫星轨道精度、地形精度、时空去相关以及其他因素，如大气延迟，电离层等，而轨道精度是影响形变测量精度的主要因素。对于两通(two-pass)差分测量，外部数字高程模型(DEM)的精度也是影响形变测量精度的另一重要因素。此前已有学者以The European Remote Sensing Satellite(ERS-1)为例，对轨道、地形和相位误差对形变测量的影响进行过研究［3］;Zebker等人［4］研究说明基线误差呈弱二次曲面影响。但这些研究都仅在理论情况下得出的，其结果仅具指导性，且不能获得这些因素影响的空间分布特征。另外不同的卫星传感器，由于雷达频率和轨道等参数的不同，这些误差源对形变结果的影响是否存在一致性也是值得认真研究的问题。ALOS PALSAR因其L波段波长较长，受地物影响较小等，在地壳运动、火山、滑坡等研究方面有着广泛的应用，特别在地震的同震形变测量方面应用较多［5-7］。然而，由于该卫星轨道精度较低，定量评估上述因素对该卫星的InSAR测量精度的影响是评价ALOS PALSAR形变测量精度的关键。因此本文拟分别从理论和实践两方面对影响形变测量精度的因素(基线和地形)进行深入探讨，以获取基线和地形误差对ALOS PALSAR形变测量精度的影响情况。首先从理论上分析基线和地形误差对形变测量的影响;其次利用汶川震区的ALOS PALSAR雷达影像，在建立评价模型的基础上，对以上两种误差引起的InSAR形变测量误差进行估计，确定无精密轨道支持下的ALOS PALSAR基线误差和地形误差对InSAR形变测量精度影响的空间分布特征，定量化评估两种误差对形变测量精度的影响。这些研究将是评价ALOS PALSAR形变测量精度的基础。

2 基线和地形误差理论分析

2.1 基线误差

由于卫星轨道误差是系统误差［4］，而基线是由两不同卫星轨道获得的，因此基线误差也具系统性，这种系统误差可以通过一定的处理方法加以消除或者减弱。我们更加感兴趣的是基线误差引起的不同地面点形变量的误差的变率，简称相对误差［3］，尤其是近距点和远距点误差之差。图1给出了重复轨道InSAR测量原理示意图［8］。A1和A2分别代表两不同卫星位置，其中，B、Bx，By、B⊥、B∥分别是基线、水平基线、垂直基线、有效垂直基线、有效平行基线; ρ、δρ分别代表卫星在A1点到地面测点的距离及不同的两个位置到同一地面点的距离之差;θ为卫星视角，α为轨道倾角。h地面高程，H为卫星高度。

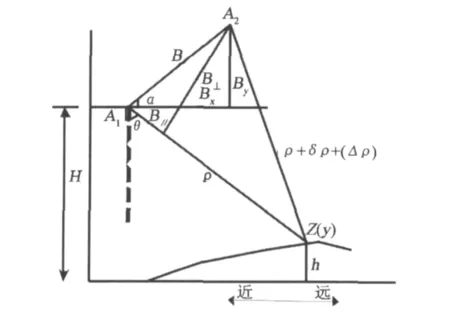
图1 重复轨道InSAR测量几何关系Fig.1 Simplified interferometric SAR geometry

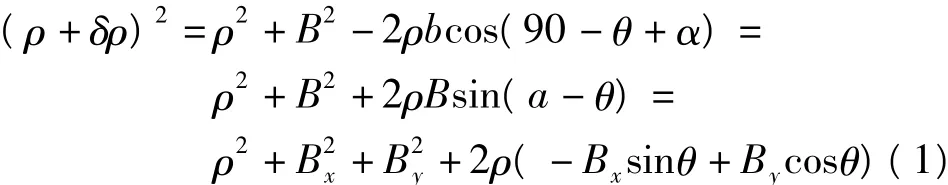
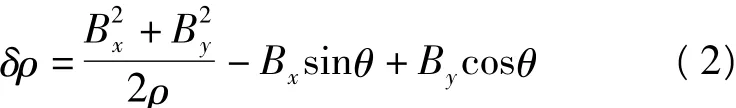
由重复干涉测量的相位-距离转换公式，则可得到相位差

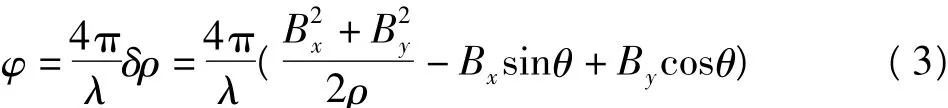
利用几何关系，可得到地面高程h为:

如果重复飞行期间发生地表形变，并设定地表形变量在卫星视线向投影为Δρ(图1)，简称形变量，则重复测量的相位差φ应该为:

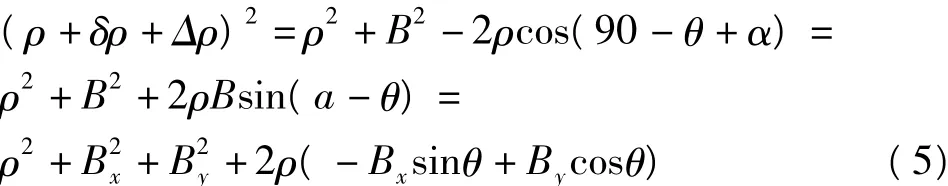
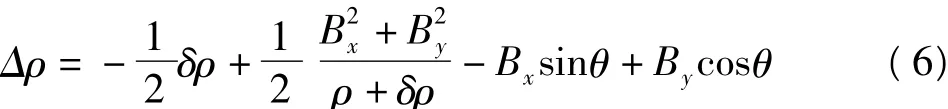
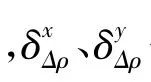
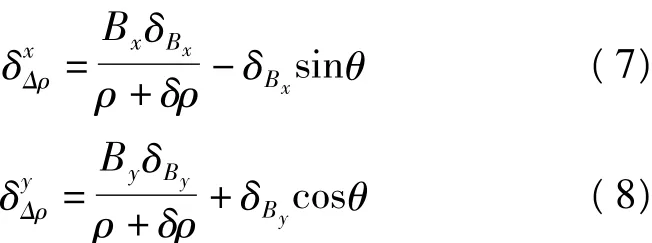
指示 Bx、By微分表达式。考虑到 Bx/ρ≪1 000/ 850 000=0.001 2，略去微小项有:

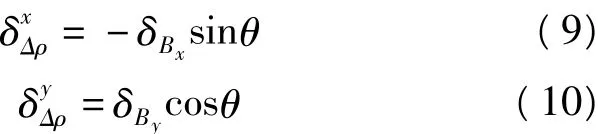
可以看出，基线误差引起的地表形变测量误差呈系统性，并且与卫星视角相关。由于其系统性，评估其影响的空间分布特征更具现实意义。Bx、By误差引起地表形变量相对误差分别为:

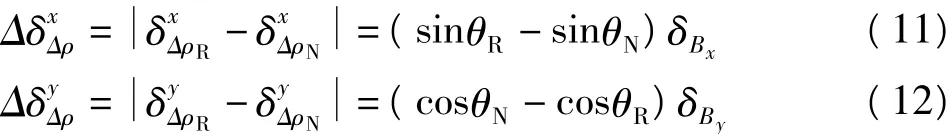
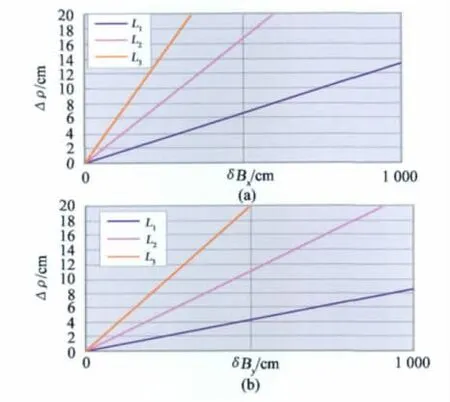
图2 基线误差对形变量Δρ的影响Fig.2 Influence of the baseline errors on surface deformation measurment

为了模拟不同视角条件下基线误差对形变结果的影响，先设ALOS PALSAR几何参数，距离ρ，波长λ，卫星视角θ0和平台高度H分别为ρ=844 000 m、λ=0.236 m、θ0=34.3°、H=698 000 m。视角的不同则对应的测区范围的变化，因此本文取θ分别为33°、34°和36°，以近距为基准，大约对应于测区宽度L分别为10 km、25 km和50 km进行模拟计算。图2给出了基线误差在不同测区范围对形变量测量精度的影响。其中L1=10 km、L2=25 km、L3=50 km，可以看出Bx对Δρ影响是By影响的1.5倍。测区范围越大则基线误差对形变测量精度的影响越大。当区域范围为50km，水平和垂直基线误差均为10 m时，对Δρ的影响分别达到60 cm和40 cm。因此对于ALOS PALSAR要获取1 cm的形变精度，则需要优于10 cm的基线精度，也说明基线精度是制约ALOS PALSAR地壳形变监测精度重要因素。

2.2 地形精度

对公式(4)、(6)分别求h的微分，有

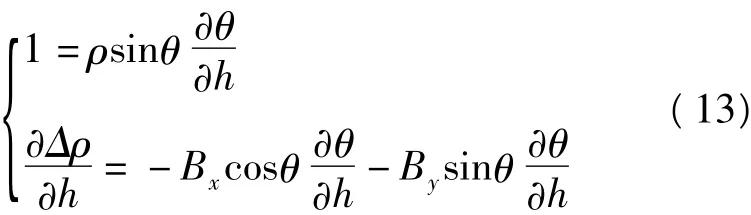
解方程得到

可以看出，DEM高程误差对形变测量精度的影响，正比于有效垂直基线B⊥，反比于距离ρ和卫星视角θ。有效垂直基线越长，误差影响越大;距离和角度越大，误差影响越小。说明DEM高程误差的影响也存在系统性。式(15)给出了DEM误差引起形变误差的相对误差。

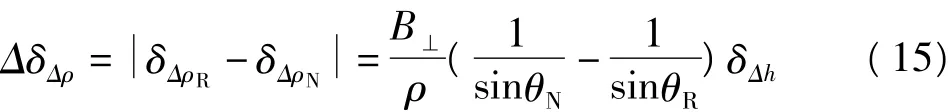
其中，θN、θR分别代表近距和远距时的卫星视角(θN=32°，θR=36°)，B⊥为有效垂直基线。

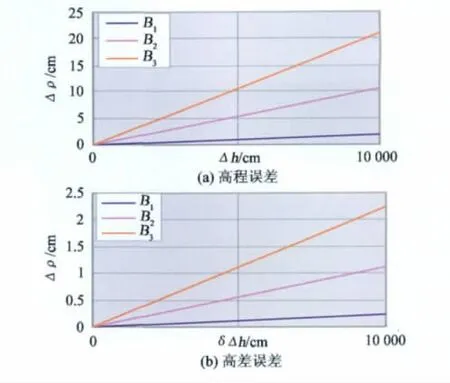
图3 DEM高程及高差误差对形变测量精度的影响Fig.3 Influence of height and height difference errors on surface deformation measurment

图3分别给出了不同有效基线条件下，外部DEM精度引起形变量的绝对误差和相对误差。其中设定有效垂直基线B⊥分别为B1=100 m，B2= 500 m，B3=1 000 m，ρ=844 000 m，测区宽度L=50 km。可以看出，有效垂直基线B⊥越长，地形误差对形变测量精度影响越大，其中高程误差对形变量测量精度的影响接近10倍于高程相对误差对观测精度的影响。因此在差分测量中需要选择有效基线较短的像对。图3给出的是可能出现的各种极限情况，在实际处理中采用的SRTM DEM作为两通差分干涉测量的外部DEM，其绝对精度一般优于16 m。可以得出在以上三种有效基线条件下，形变测量误差分别为0.34 cm、1.68 cm、3.36 cm。高程相对误差对形变测量精度的影响分别为0.035 cm、0.18 cm、0.36 cm。因此也进一步说明了在当前DEM精度情况下，要获得1 cm的形变监测精度，需要选择有效垂直基线的长度最好小于300 m。

3 基线和DEM误差对形变测量的影响的空间分布

根据理论上分别对基线误差和DEM误差引起形变测量精度分析可以得出，要获得高精度的形变监测结果，要求高精度基线，选择合理的干涉像对(如基线长度，时间间隔等)，在进行两通差分时，还需选择精度较高的外部DEM。以上获得的结果只具有指导性。定量化评价两种误差对结果的影响，特别是这些误差对结果影响的空间分布特征是ALOS PALSAR形变测量精度评定的关键。因此需要研究一套切实可行的方法来分析和评价两种误差影响的空间分布特征。

由于ALOS PALSAR raw1.0格式的雷达影像未提供精密的轨道，因此在实际处理过程中，需要采用基线重估计处理方法来消除或减弱轨道误差的影响［9-12］。本文也将利用该技术来估计基线误差和DEM误差对形变结果的影响。如果假设形变测量误差δ△LOS可由式(16)表示，主要包括基线误差δB、DEM误差δDEM、相位测量误差δφ以及其他误差(如电离层、大气延迟等)。

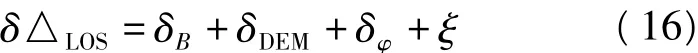
分别获取基线估计前后的经解缠的形变影像，设定两次解缠的其他参数一致，因此可以假设其他3个因素的影响在两次解缠过程中的影响一致，再对基线估计前后的解缠影像相差处理，可消除其他3个因素的影响，差分图像则为基线误差引起的误差。在进行DEM误差评定时，则利用两种不同高程的DEM，分别进行两次解缠处理，误差项中除DEM影像，其他项在两次解缠过程中的影响相同，因此对两解缠影像相差处理，可获得DEM误差对形变量的影响。

主要技术流程(图4)是首先采用两通差分干涉测量方法对像对进行处理［5，8］，然后利用外部DEM和解缠后的总相位对基线进行重新估计，再进行两通差分处理。分别获得了基线重新估计前后形变影像。另外为了评估不同精度的DEM对结果的影响，本文利用SRTM DEM提取了两种高程基准的数字高程模型，一种的高程基准是似大地水准面，而另一种是参考椭球面。利用这两种DEM分别进行两次差分处理，获得基于不同DEM的形变分布图。利用这些形变分布图可分析和研究ALOS PALSAR的基线精度和DEM精度对形变测量精度的影响。

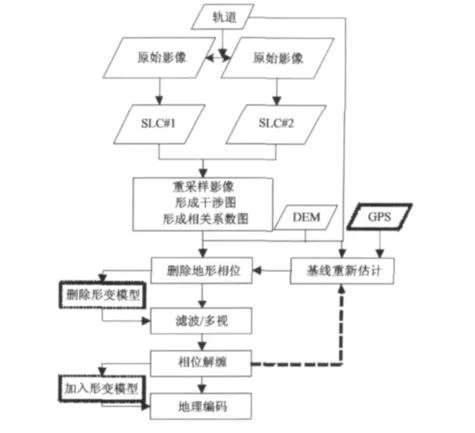
图4 两通差分干涉测量流程及策略Fig.4 Flow chart and processing strategies of two-pass interferometry

为了充分考虑不同基线、不同轨迹对形变结果的影响程度，本文基于以下4个标准选择干涉雷达像对:1)选择不同基线;2)影像对在重复测量期间无明显的地表形变;3)选择丘陵、平原地区的影像，减少地形及植被对相位测量精度的影响;4)为了充分评价不同轨道条件下，上述参数对结果的影响，选择了不同轨道的3幅干涉像对进行分析。干涉雷达像对基线参数见表1。

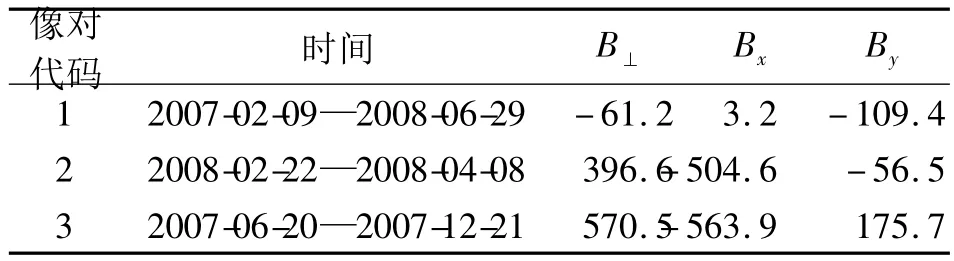
表1 干涉像对的参数(单位：m)Tab.1 Parameters of interferometry(unit：m)

4 结果分析

由于选择的干涉像对在成像期间地表未发生明显形变，因此在进行两通差分后，获得的形变量分布图被认为是误差分布图，主要包括相位测量误差、基线误差和DEM误差及其他误差(如电离层、大气延迟等)。进行基线重新估计后再进行的差分干涉测量结果则主要包含的是相位测量误差和DEM误差及其他误差。对同一外部DEM的两次差分处理结果再进行相差处理，则可获得基线误差的空间分布。对不同DEM条件下的解缠相位图进行相差处理，即可获得DEM误差对形变测量精度的影响。

图5分别给出了像对2(表1)干涉测量及基线估计后的形变相位分布图，其中图(a)、(b)、(c)分别为基线估计前的相位分布、基线估计后相位的分布和以上两相位分布的差分结果。(e)、(f)、(g)分别对应于(a)、(b)、(c)图中表示的剖面线。单位是弧度，乘以λ/4π，即可换算成视线距离(LOS)。从图中可以看出，基线估计前相位残差分布呈现系统变化，由近距到远距分别从2.5～-6.0(图(a)、(e))。基线纠正后，残差分布呈现随机分布特征。大小在-1～1之间(图(b)、(f))。获得的轨道误差从-5～2变化。对图(c)的统计发现最大值为-5.5，转换到距离单位则为-10.3 cm。说明基线产生的最大误差为10.3 cm。根据式(11)、(12)可得到最大基线误差为2.57 m。同样对另外两像对进行统计发现，基线最大误差分别为13.9 cm与17.8 cm，对应最大基线误差为3.47 m、4.25 m。通过对3个不同轨迹的ALOS PALSAR的基线精度的评价可以得出，ALOS PALSAR的轨道精度为3～5 m。也说明在无精密轨道支持下，ALOS PALSAR两通InSAR测量结果的精度较差，因此必须对基线进行重新估计，消除或减弱轨道误差对形变测量精度的影响。

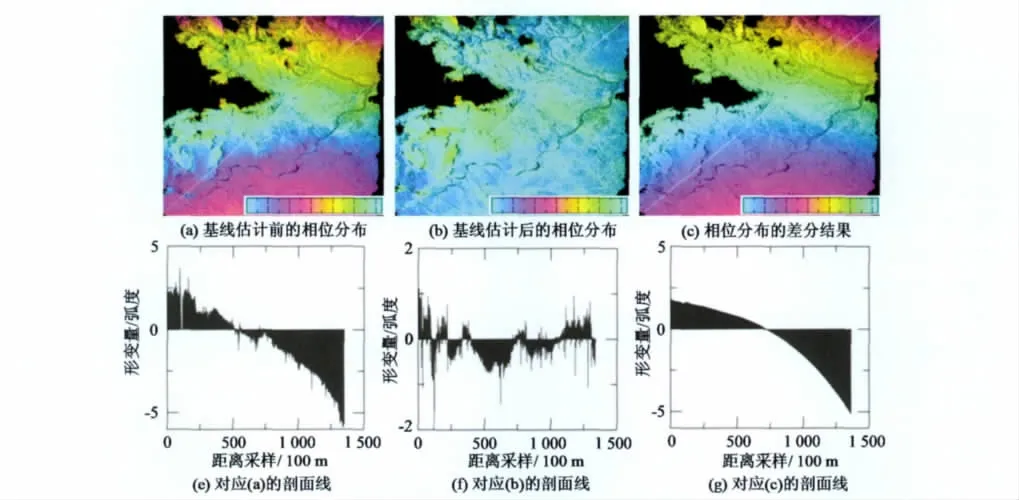
图5 基线估计前后残差分布Fig.5 Residual distribution before and after baseline estimation

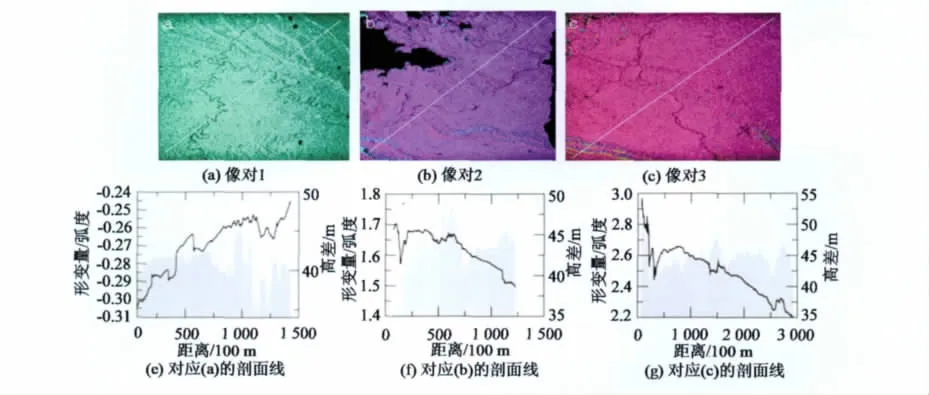
图6 DEM误差引起的形变测量误差Fig.6 Residual distribution of terrain errors

图6给出了3组像对DEM误差对形变测量的评价结果，其中图6(e)、(f)、(g)分别对应于图6 (a)、(b)、(c)中线条所示位置的剖面线。图6(e)、(f)、(g)左纵轴代表是DEM误差引起的形变误差。右纵轴代表对应位置两DEM的高差。DEM对像对1、2、3中影响分别为-0.28(-0.5 cm)、1.6(3.0 cm)、2.5(4.7 cm)。3幅影像覆盖范围的两DEM高差变化为40～45 m。从图中可以明显看出，DEM误差的影响差异较大，对照表1，可以看出有效垂直基线越长，则DEM误差对结果的影响越大，因此要获得1 cm的形变精度，则要求有效垂直基线小于150 m。对于现有的SRTM DEM，其高程精度优于16 m，在基线小于400m的情况下，DEM引起的误差小于1 cm。这也说明了差分测量中的DEM误差对形变测量精度的敏感性较低。

5 结语

分别从理论和实际对影响InSAR形变测量因素的基线精度和 DEM精度进行分析探讨，得出ALOS PALSAR的轨道精度为3～5 m，要使InSAR形变测量结果具可量测性，必须对基线进行纠正，消除或减少基线误差对结果精度的影响。DEM误差对形变量的影响根据有效基线的不同差异较大。对于现有的SRTM DEM情况下，有效垂直基线小于400m的像对时，DEM误差对形变测量结果的影响可以忽略。

致谢 感谢Jaxa提供的ALOS PALSAR雷达影像!

1 Massonnet D，et al.The displacement field of the Landers earthquake mapped by radar interferometry［J］.Nature，1993，364:138-142.

2 Klees R and Massonnet D.Deformation measurement using SAR interferometry:Potential and limitations［J］.Geologie en Mijnbouw，1998，77(2):161-176.

3 李振洪，刘经南，许才军.InSAR数据处理中的误差分析［J］.武汉大学学报(信息科学版)，2004，29(1):72-76.(Li Zhenhong，Liu Jingnan and Xu Caijun.Error analysis in InSAR data processing［J］.Geomatics and Information Science of Wuhan University，2004，29(1):72-76)

4 Zebker H A，et al.Accuracy of topographic maps derived from ERS-1 interferometric radar［J］.IEEE Transactions on Geoscience and Remote Sensing，1994，32:823-836.

5 Shen Zhengkang，et al.Slip maxima at fault junctions and rupturing of barriers during the 2008 Wenchuan earthquake［J］.Nature Geoscience，2009，2:718-724.

6 沈强，谭凯.日本Mw9.0地震多传感器InSAR形变初步分析［J］.大地测量学与地球动力学，2011，(5):21-25.(Shen Qiang and Tan Kai.Characteristic analysis of coseismic deformation from InSAR images［J］.Journal of Geodesy and Geodynamics，2011，(5):21-25)

7 Manabu Hashimotoa，Mari Enomotoa and Yo Fukushima.Coseismic deformation from the 2008 Wenchuan，China，Earthquake Derived from ALOS/PALSAR Images［J］.Tectonophysics，2010，491(1-4):59-71.

8 舒宁.雷达影像干涉测量原理［M］.武汉大学出版社，2003.(Shu Ning.Principles of rader interferometry［M］.Wuhan:Press of Wuhan University，2003)

9 A Monti Guarnieri，et al.Accurate and robust baseline estimation［A］.Proceedings of ESA Fringe’99［C］.Available on the WEB at the URL:http://home.dei.polimi.it/monti/papers/fringes99_mg.pdf.

10 Kuldip S，et al.Baseline estimation in interferometric SAR［J］.Geoscience and Remote Sensing，1997，1:454-456.

11 Nico G.A baseline estimation algorithm for SAR interferometry［A］.Proceedings of ESA Fringe’97，1997［C］.A-vailable on the WEB at the URL:http://earth.esa.int/ workshops/ers97/papers/singh/.

12 郑芳，邬钧霆，马德宝.基于轨道误差的基线估计及其对高程精度的影响［J］.信息工程大学学报，2005，6(1):77 -79.(Zheng Fang，Wu Junting and Ma Debao.Baseline estimation based on the track error and the effect on height decision［J］.Journal of Information Engineering University，2005，6(1):77-79)

ERROR ANALYSIS OF BASELINE AND TERRAIN IN InSAR DATA PROCESSING USING ALOS PALSAR

Shen Qiang1)，Qiao Xuejun2)，Jin Yinlong3)，Wang Hansheng1)and Jiang Liming1)

(1)State Key Laboratory of Geodesy and Earth’s Dynamics，Institute of Geodesy and Geophysics，CAS，Wuhan 430077 2)Institute of Seismology of China Earthquake Administration，Wuhan 430071 3)State Key Laboratory of Water Resources and Hydropower Engineering Science，Wuhan University，Wuhan 430072)

Seeing that there are still many factors governing the accuracy of InSAR although they have appeared to good application in various field as earthquake，landslide，etc.this paper focus on the two sources of errors controlling the accuracy of InSAR.In the first place，theoretical analysis has been first made for the evaluation of influence of baseline and terrains errors on surface deformation.On the basis of above theoretical analysis，we estimated the influence of baseline errors and terrain errors on InSAR for ALOS PALSAR radar images without accurate orbit information.The spatial patterns of additional surface deformation due to the two error sources have also been retrieved.The results show that the orbit accuracy of ALOS PALSAR is 3-5 m，in which the displacements must be rectified for the low orbit accuracy.The simulation and experimentation all show that baseline is main error sources in the use of ALOS PALSAR and terrain errors is negligible.For the accuracy of better than 1 cm in deformation measurements，the length of baseline must be less than 400 m under current SRTM DEM if two-pass interferometry was used.

ALOS PALSAR;InSAR;baseline errors;terrain errors;length of baseline

1671-5942(2012)02-0001-06

2011-12-21

水资源与水电工程科学国家重点实验室开放基金(2009B054);国家自然科学基金(41004008，40825012);冰冻圈国家重点实验室开放基金(SKLCS 09-03)

沈强，1980年生，博士，副研究员，现从事卫星遥感地壳形变研究.E-mail:cl980606@hotmail.com

P227

A