污染物在填埋场底部非饱和土中的一维扩散解析解
关驰,谢海建,,陈云敏,唐晓武,楼章华
(1.浙江大学 建筑工程学院,浙江 杭州 310058;2.浙江大学 软弱土与环境土工教育部重点实验室,浙江 杭州 310058)
为防止和减缓降雨入渗和垃圾自身降解等产生的高污染物浓度填埋场渗滤液对地下水造成的污染,必须对渗滤液扩散引起的地下水污染问题进行研究与评价[1-7]。虽然填埋场渗滤液对地下水的污染问题可以通过数值模型分析和求解[8-10],但解析解在许多方面是代替数值方法的一种经济、有效的方法[11-12]。一方面解析解是数值解的理论基础[13];另一方面,数值方法的复杂程度往往较高(尤其在填埋场的初步设计阶段),采用详尽的数值模拟及其必要的发散性检查所需要的代价(按工时)往往不合算[14]。
Liu and Ball[15]和Foose等[16]获得了半无限空间污染物在土中的一维扩散解析解。Shackelford and Lee[17],陈云敏等[18],谢海建等[19]和Li and Cleall[20]分别针对不同的边界条件和土层的分层性等因素,得到了有限厚度边界时污染物在土中的一维扩散解析解。但这些解析解均基于饱和土层,许多情形下填埋场底部的防渗层是非饱和的[21-22]。Fityus等[21]对已有填埋场的调查发现,土层体积含水量达到稳态需要的时间远小于填埋场污染物的运移时间;因此假设填埋场底部土层中体积含水量稳态分布是合理的,且由此导致的误差可以忽略。对每一单层土而言,线性体积含水量分布是分析非饱和土中体积含水量分布的实用和简便的方法[21]。以往学者主要针对污染物在非饱和含水层中的运移问题进行研究,水力梯度引起的对流作用和机械弥散作用往往是这类问题的主导作用,而分子扩散作用则往往被忽略[23]。因此,基于此得到的污染物在非饱和含水层中运移的解析解不能用于分析污染物在填埋场底部粘性土中的运移问题。
本文在假设填埋场底部非饱和土层内体积含水量线性分布的条件下,建立了污染物在填埋场底部非饱和土中的扩散模型,利用分离变量法结合广义正交理论得到了该模型的解析解。通过与多物理场耦合分析软件COMSOL Multiphysics 4.2[24]的计算结果比较,验证了本文解析解的正确性和有效性。基于该解析解,研究了土层体积含水量变化对污染物击穿非饱和土的影响。该解析解可用于数值模型的验证和试验数据的拟合等。
1 数学模型
1.1 基本假设
假设渗滤液中污染物浓度保持不变,为C0。底部的污染物浓度为0或污染物通量为0。并假设竖直向下为z的正方向,且z轴的原点在非饱和土顶端,土层厚度为L(见图1)。
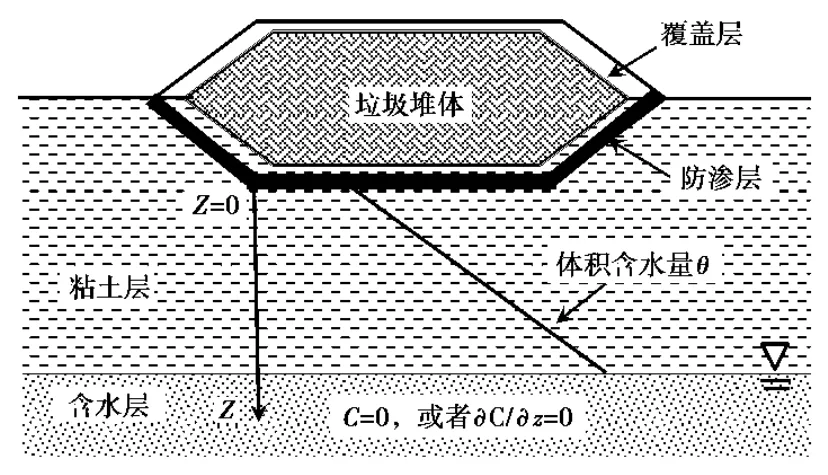
图1 污染物在非饱和土中运移模型
该模型的主要假设有:(1)污染物在非饱和土层中运移是一维的;(2)土层是均质的;(3)仅考虑污染物在非饱和土中的扩散作用,不考虑对流作用的影响;及(4)土层体积含水量是深度的线性函数。
1.2 控制方程及边界条件
在上述假设条件下,污染物在非饱和土中的一维扩散控制方程为[21,25]:
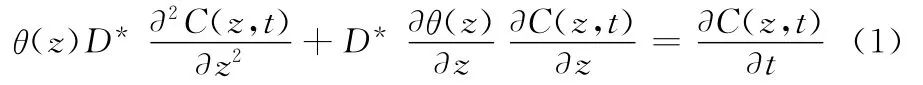
其中C(z,t)为土层孔隙水中污染物浓度(mg/L),随深度z和时间t变化;D*为污染物在非饱和土中的有效扩散系数(m2/s);θ(z)为体积含水量,即单位体积土体中水的含量;这里假设其为深度的线性函数[21]

其中A、B为常数。
将式(2)代入式(1),得到:

式(3)即为假设体积含水量线性变化时污染物在非饱和土中的扩散方程。
当上部污染物浓度C0不变时,上边界条件为:

若下边界保持污染物浓度为0,则下边界条件为:

当土层下方含水层的水流流速较大以致能及时带走渗漏出的污染物时,适宜采用上述零浓度边界条件。
若土层底部通量为零,则下边界条件为:

当粘土衬垫的下卧含水层流速很小,或其下卧层是不透水的基岩时,可采用这种边界条件。
在初始时刻,土层中污染物浓度假设为深度的某一函数:

其中f(z)为初始时刻非饱和土中污染物的浓度分布函数。
2 模型的解
在满足边界条件式(4)~(6)和初始条件式(7)下,控制方程(3)的解为(详细的求解过程见附录):
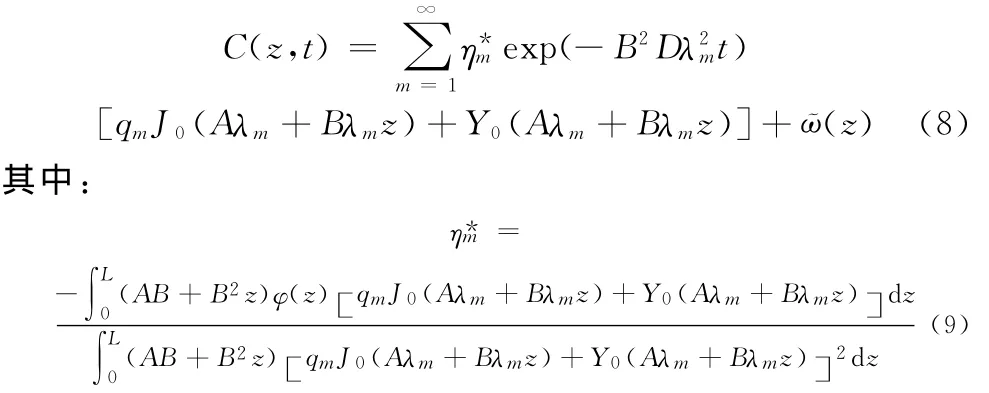
J0为0阶第一类贝塞尔函数,Y0为0阶第二类贝塞尔函数,λm为方程的第m个特征根。
在式(8)浓度解的基础上,可通过下式得到任意时刻t和任意位置z处污染物的通量J:

当下边界为零浓度时:

或当下边界为零通量时:

由式(8)可知,当t→∞时,即在稳态时,污染物的浓度分布即为φ(z)。
3 与数值解及饱和时解的比较
为了验证本文解析解的有效性和合理性,比较了本文解和多物理场耦合分析软件 COMSOL Multiphysics 4.2[24]的计算结果。计算比较时模型相关参数参考文献[21],取土层顶部体积含水量为0.36,底部为0.3795,土层厚度0.75m,扩散系数D*为5×10-10m2/s。如图2所示,经过10年时间的运移,由本文解得到的污染物浓度结果和对应数值计算结果符合得很好,这说明了本文解的正确性。
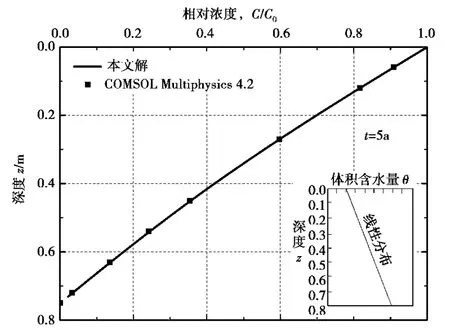
图2 本文解与数值解的比较
图3为在底部边界为零浓度情况下改变上下体积含水量分别为0.3和0.6时,土层污染物相对浓度变化曲线本文解及饱和情况解比较,发现本文非饱和时解在同一深度较饱和时的解结果偏小,说明相对饱和土,污染物在非饱和土中随深度增加其相对浓度变化较慢。
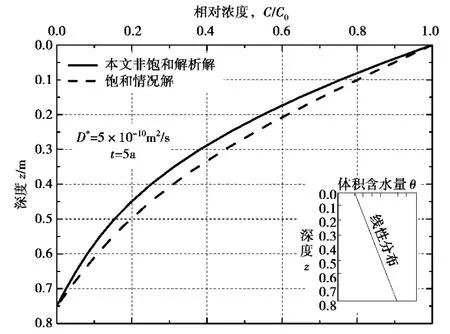
图3 非饱和与饱和土中污染物相对浓度曲线
图4为底部零浓度边界条件下本文非饱和土的解与饱和时的解在土底端通量上的比较,非饱和土时顶端体积含水量为0.3,底端体积含水量为0.6,饱和时的孔隙度分别取为0.3和0.6。非饱和土底端污染物通量击穿曲线介于饱和度0.3和0.6得到的通量击穿曲线之间。100年时非饱和土底端污染物通量为91g·ha-1·a-1,是孔隙度为0.3时饱和土底端通量(63g·ha-1·a-1)的1.4倍,是孔隙度为0.6时通量(126g·ha-1·a-1)的0.7倍。这也说明非饱和土的体积含水量对污染物的通量击穿曲线影响较大。

图4 饱和与非饱和土层底端污染物通量
4 参数分析
为了从理论上考察土层不同体积含水量分布对污染物扩散的影响,本文选取了四种不同体积含水量分布。粘土孔隙率变化范围为0.1-0.8[27]。本文选取各工况体积含水量取值见表1。工况1为土层顶部和底部体积含水量分别为0.3和0.6。工况2与工况1相反,即体积含水量在顶部和底部分别为0.6和0.3。工况3和4与工况1和2类似,仅土层上下部的体积含水量分别为0.5和0.55。

表1 四种工况体积含水量取值
图5为四种不同工况下土层底部污染物相对浓度随时间的变化曲线,即浓度击穿曲线的变化。分析表明工况3和4结果介于工况1和2之间,曲线形状非常类似。当非饱和土顶端体积含水量小于底端体积含水量时(工况1和3),经过5年时间的运移,达到非饱和土底端的污染物相对浓度较小;相反地,当非饱和底端体积含水量大于底端体积含水量时(工况2和4),经过相同时间,达到非饱和土底端污染物相对浓度较大。经过10年时间的运移,工况1和3达到非饱和土底端的相对浓度较小,分别为0.29和0.33。工况2和4对应的相对浓度较大,分别为0.44和0.40。这说明当非饱和土顶端体积含水量小于底端体积含水量时,污染物在该种条件下扩散运移地较慢;相反,在非饱和土顶端体积含水量大于底端体积含水量时,污染物运移较快。
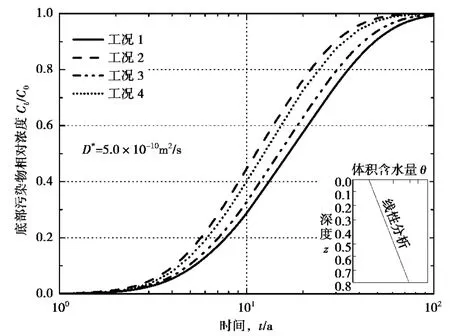
图5 不同工况污染物浓度击穿曲线比较
图6为不同工况下非饱和土底部污染物通量随时间的变化曲线。工况1和2的底部通量差别不大。工况3和4的通量击穿曲线在10年之前有所差别,但10年后逐渐趋于一致。不同于浓度击穿曲线,土层上下端体积含水量变化较小的工况,即工况3和4的底部污染物通量较大,100年时其通量是工况1和工况2的1.09倍。
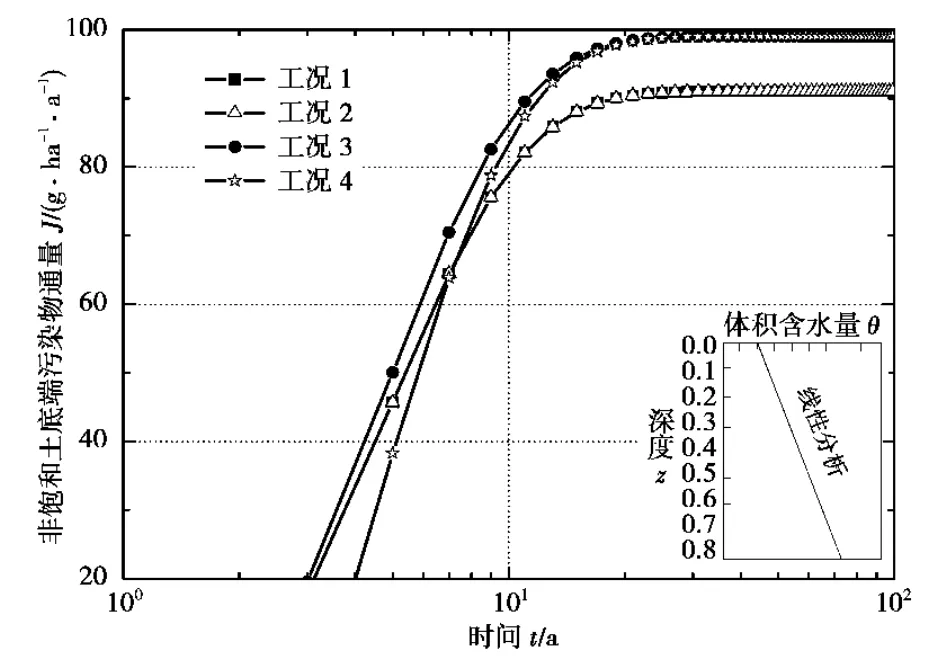
图6 不同工况非饱和土底部污染物通量击穿曲线比较
5 结 论
本文在假设土层体积含水量随深度呈线性分布的基础上,根据污染物在非饱和土中的扩散模型,利用分离变量法结合及广义正交理论得到了该模型的解析解。通过与数值解法的比较验证本文模型解的合理性。基于该解析解本文分析了土层不同体积含水量分布时污染物通过非饱和土的浓度和通量击穿曲线,得到的主要结论有:
(1)本文解的计算结果和饱和情形的解的结果比较发现体积含水量变化对污染物运移影响较大;且随着时间的增大,本文解得到的污染物浓度曲线逐渐接近稳态的情形,说明了本文解的正确性和合理性。
(2)污染物在非饱和土中的扩散较其在饱和土中慢。当土层上下端体积含水量分别为0.3到0.6时,5年后0.3m深处非饱和土中污染物相对浓度为0.38,而饱和土时为0.45。控制填埋场底部土层的饱和度有利于填埋场的防污。
(3)体积含水量的线性变化对非饱和土底部污染物通量变化影响较大,分别为饱和时最大体积含水量和最小体积含水量对应的土层底部污染物通量的0.7和1.4倍。
(4)当非饱和土层顶端体积含水量小于底端体积含水量时,污染物在非饱和土中扩散运移较慢;相反,当顶端体积含水量大于底端体积含水量时,污染物运移较快。
[1]郭永龙,王焰新,蔡鹤生,等.垃圾填埋场渗滤液对地下水环境影响的评价[J].地质科技情报,2002,21(1):87-92.Guo Y L,Wang Y X,Cai H S,et al.Assessment of environment impact of leakage of landfill site on ground water[J].Geological Science and Technology Information,2002,21(1):87-92.
[2]张文杰,陈云敏,詹良通.垃圾填埋场渗滤液穿过垂直防渗帷幕的渗漏分析[J].环境科学学报,2008,28(5):925-929 Zhang W J,Chen Y M,Zhan L T.Transport of leachate through vertical curtain grouting in landfills[J].Acta Scientiae Circumstantiae,2008,28(5):925-929.
[3]马志飞,安达,姜永梅,等.某危险废物填埋场地下水污染预测及控制模拟[J].环境科学,2012,33(1):64-70.Ma Z F,AN D,Jiang Y M,et al.Simulation on Contamination Forecast and Control of Groundwater in a Certain Hazardous Waste Landfill[J].Chinese Journal of Environmental Science,2012,33(1):64-70.
[4]冯世进,高丽亚,王印.垃圾填埋场边坡上土工膜的受力分析[J].岩土工程学报,2008,30(10):1484-1489.Feng S J,Gao L Y,Wang Y,et al.Analysis of tension of geomembranes placed on landfill slopes[J].Chinese Journal of Geotechnical Engineering,2008,30(10):1484-1489.
[5]Liu C L,Zhang F E,Zhang Y,et al.Experimental and numerical study of pollution process in an aquifer in relation to a garbage dump field[J].Environmental Geology,2005,48(8):1107-1115.
[6]Dong J,Zhao Y S,Zhang W H,et al.Laboratory study on sequenced permeable reactive barrier remediation for landfill leachate-contaminated groundwater[J].Journal of Hazardous Materials,2009,161(1):224-230.
[7]薛强,赵颖,刘磊,等.垃圾填埋场灾变过程的温度-渗流-应力-化学耦合效应研究[J].岩石力学与工程学报,2011,30(10):1970-1988.Xue Q,Zhao Y,Liu L,et al.Study of thermo-hydro-mechanical-chemical coupling effect of catastrophe process of landfill[J].Chinese Journal of Rock Mechanics and Engineering,2011,30(10):1970-1988.
[8]Rowe R K,Quigley R M,Brachman R W L,et al.Barrier Systems for Waste Disposal[M].London and New York:Spon Press,2004
[9]黄冠华,黄权中,詹红兵,等.均质介质中污染物迁移的分数微分对流 弥散模拟[J].中国科学D辑:地球科学,2005,35(增刊I):249-254.Huang G H,Huang Q Z,Zhan H B,et al.Simulation of contaminants advection-diffusion in homogeneous medium [J].Science in China Series D:Earth Sciences,2005,35(Suppl):249-254.
[10]何俊,高子坤,詹国才.有机污染物在复合衬垫中的运移分析[J].水文地质工程地质,2009,1:124-127.He J,Gao Z K,Zhan G C.Transport of organic contaminants through a composite liner[J].Hydrogeology and Engineering Geology,2009,1:124-127.
[11]谢海建,陈云敏,楼章华.污染物通过有缺陷膜复合衬垫的一维运移解析解[J].中国科学:技术科学,2010,40(5):486-495.Xie H J,Chen Y M,Lou Z H.An analytical solution to contaminant transport through composite liners with geomembrane defects[J].Science China Technological Sciences,2010,40(5):486-495.
[12]谢海建,楼章华,陈云敏,等.污染物通过GCL/AL防渗层的对流-弥散解析解[J].科学通报,2010,55(21):2148-2155.Xie H J,Lou Z H,Chen Y M,et al.An analytical solution to contaminant advection and dispersion through a GCL/AL liner system [J].Chinese Science Bulletin,2010,55 (21):2148-2155.
[13]Park E,Zhan H B.Analytical solutions of contaminant transport from finite one-,two-,and three-dimensional sources in a finite-thickness aquifer[J].Journal of Contaminant Hydrology,2001,53(1-2):41-61
[14]Rowe R K,Nadarajah P.An analytical method for predicting the velocity field beneath landfills[J].Canadian Geotechnical Journal,1997,34:264-282.
[15]Liu C X,Ball W P.Analytical modeling of diffusion-limited contamination and decontamination in two-layer porous medium[J].Advances in Water Resources,1998,21:297-313.
[16]Foose G J,Benson C H,Edil T B.Analytical equations for predicting concentration and mass flux from composite liners[J].Geosynthetics International,2001,8(6):551-575.
[17]Shackelford C D,Lee J M.Analyzing diffusion by analogy with consolidation[J].Journal of Geotechnical and Geoenvironmental,2005,131(11):1345-1359.
[18]陈云敏,谢海建,柯瀚,等.层状土中污染物的一维扩散解析解[J].岩土工程学报,2006(4):521-524.Chen Y M,Xie H J,Ke H,et al.Analytical solution of contaminant diffusion through multi-layered soils [J].Chinese Journal of Geotechnical Engineering,2006(4):521-524.
[19]谢海建,唐晓武,陈云敏,等.原始土层影响下成层介质污染物一维扩散模型[J].浙江大学学报(工学版),2006(12):2191-2195.Xie H J,Tang X W,Chen Y M,et al.One-dimensional model for contaminant diffusion through layered media[J].Journal of Zhejiang University (Engineering Science),2006 (12):2191-2195.
[20]Li Y C,Cleall P J.Analytical solutions for contaminant diffusion in double-layered porous media[J].Journal of Geotechnical and Geoenvironmental,2010,136(11):1542-1554
[21]Fityus S G,Smith D W,Booker J R.Contaminant transport through an unsaturated soil liner beneath a landfill[J].Canadian Geotechnical Journal,1999,36:330-354
[22]Bonaparte R,Gross B A.Field behavior of double liner systems.In:Bonaparte R eds.Waste containment systems:construction,regulation and performance[J].New York:ASCE Geotechnical Special Publication,1990.52-83.
[23]Sander G C,Braddock R D.Analytical solutions to the transient,unsaturated transport of water and contaminants through horizontal porous media [J].Advances in Water Resources,2005,28(10):1102-1111.
[24]COMSOL Multiphysics:Engineering simulation software.Version 4.2.Burlington:COMSOL,Inc,2011.
[25]席永慧.锌和镍在粉煤灰-粘土介质中扩散系数的测定[J].同济大学学报:自然科学版,2007,35(11):1520-1524.Xi Y H.Determination of Diffusion Coefficients of Zn2+and Ni2+in saturated fly ash-clay medium[J].Journal of Tongji U-niversity:Natural Science,2007,35(11):1520-1524.
[26]zisik M N.Heat conduction[M].2nd edition.New York:John Wiley and sons,1993.
[27]袁聚云.土质学与土力学[M].人民交通出版社.北京,2009.
附 录
令x=A+Bz,则z=(x-A)/B,从而将控制方程及边界条件转化为:

为了将非齐次边界条件(A2)转化为齐次边界条件,根据叠加原理,可假设C(x,t)的解具有的形式为[26]

对零通量下边界条件(A15),控制方程(A12)解为

关于u(x,t)的求解可采用分离变量法,设控制方程(A7)的解具有的形式为

其中Γ(t)和R(x)分别为时间t和空间x的函数。
由控制方程(A7)可知,Γ(t)由下式确定
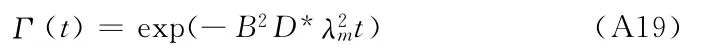
空间变量x的函数R(x)满足如下特征根方程:

其中αm为待定参数。
将式(A24)代入初始条件(A11)得到
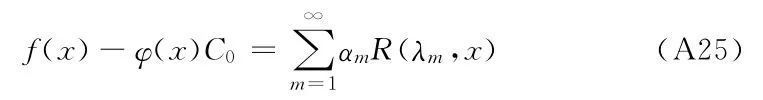
方程(A20)-(A25)是Sturn-Liouville问题的一个特例,因此R(λm,x)具有如下的正交性质[22]:
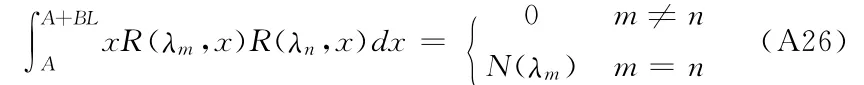
其中N(λm)由下式确定

Rm(x)是常微分方程(A20)的解,其具有的形式为
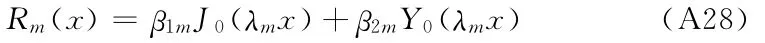
设a=A,b=A+BL;将上式代入上边界条件(A21)和下边界条件(A22)、(A23)得到:
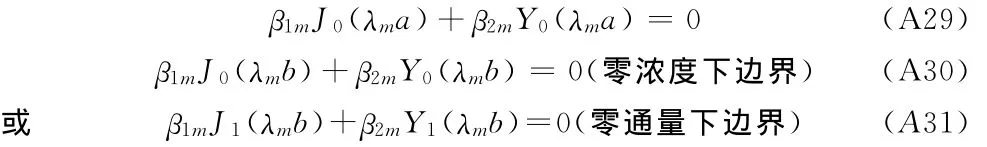
式中J1(x),Y1(x)分别为x的一阶第一类贝塞尔函数和一阶第二类贝塞尔函数。
因为β1m和β2m是不为零的参数,则由式(A29)和 (A30)或(A31)可得确定特征根λm的方程如下:

将式(A37)代入式(A24)可得:

两边同乘x[qmJ0(λmx)+Y0(λmx)]再积分并由正交关系式(A26)、(A27)可以确定ηm为
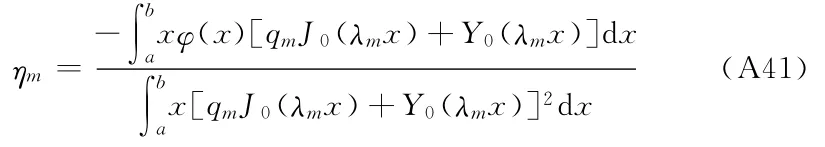
从而控制方程(A1)的解为:

将x=A+Bz代入上式即可得到控制方程(1)的解为式(8)。

