考虑结构应力的粘土一维非线性固结分析

刘 洋，宫 志，王 喆

（北京科技大学 土木与环境工程学院，北京 100083）

一维非线性固结理论的研究始于20世纪60年代，早期如Davis和Raymond[1]基于线性的e-lgp关系，假设渗透系数kv与体积压缩系数mv是同步的，得出了固结系数cv为恒定量的固结方程，并且获得了解析解。Mesri[2]等和 Barden[3]等根据试验得出e-lgp和e-lgkv经验关系，将其应用于饱和软土一维固结研究中。谢康和等[4－5]建立了逐步加荷条件下单层和双层地基一维非线性固结的解析解，并在以往研究的基础上推导了考虑了应力历史这一因素的一维非线性固结方程，其假定荷载为单级均布连续荷载，采用经验关系的e-lgp和e-lgkv非线性关系，未考虑天然土的结构性的影响。曹宇春等[6]建立了任意施工荷载下天然结构性粘土的一维非线性固结方程，但仍沿用e-lgp和e-lgkv的非线性关系。吴建等[7]同时考虑了固结过程中材料和几何非线性。Menéndez等[8]采用有限元对不可压缩流体和变渗透系数的非线性固结问题进行了分析。王俊等[9]对变渗透系数软土的一维非线性固结进行了数值模拟。商卫东和白冰[10]讨论了荷载随时间变化情况下的非线性固结问题的求解方法。邓岳保和谢康和[11]研究了互补算法在一维非线性固结求解中的应用。

沈珠江[12]指出，结构性天然粘土具有高孔隙比、强渗透性以及陡降型压缩曲线，并提出了结构应力比的概念。刘恩龙和沈珠江[13]还建立了能够反映结构性土压缩曲线在e-lgp坐标中的非线性数学关系，可用于结构性软土的沉降计算。

本文将综合考虑土的结构性和分级施工荷载影响，将lge-lgkv和lge-lgp双对数关系的非线性模型引入到一维固结的研究之中，并引用结构应力比的概念建立结构性软粘土的一维非线性固结控制方程，利用Crank-Nicolson差分法来求解，最后与不考虑土结构性的非线性固结结果和线性固结结果进行比较分析。此外，对天然结构性软粘土和超固结土而言，虽固结曲线形状不同但性状类似，因此本文的研究方法也可进一步扩展至超固结土的一维非线性问题分析。

1 考虑结构应力比的土体非线性固结

1.1 非线性压缩模型的选取

Chai[14]等指出，对于高灵敏度的天然结构性软土而言，压缩曲线在lge-lgp坐标系中的线性效果要优于在e-lgp中，其表达式如下：

式中：λ为修正压缩指数，即lg（e＋ec）-lgp直线的斜率；ec为实验参数。

大量实验结果表明：ec的变化范围在－1～1之间，当ec＝0时，模型转化为lge-lgp模型，当ec＝1时，模型转化为lg（e＋1）-lgp模型。已有研究表明，lge-lgp压缩模型能够模拟相当一部分天然土的压缩特性。故本文将使用lge-lgp压缩模型。

对于结构性土，土体受荷前期土体结构未完全破坏（p＜pc，图1中的AB段，斜率为λ，其中pc为结构应力），在外荷载作用下有效应力随着超孔隙水压力的消散而不断增长，当土体的有效应力超过结构应力时（p＞pc，图1中的BC段，斜率为η），土结构大部分破坏，故可建立分段压缩方程为：

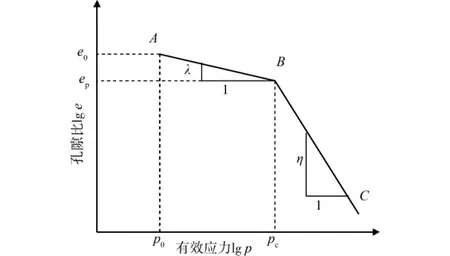
图1 结构性软土压缩曲线图

1.2 非线性渗透模型的选取

Mesri＆Olson[15]根据实验分析发现，土体孔隙比的变化范围过大时，e-lgkv渗透模型可能并不适用，因此对该模型做出了一些修正，提出了lge-lgkv渗透模型：kv＝BeA。A，B为黏土渗透特性参数。该模型也可表示为：lgkv＝lgB＋Alge。

Al-Tabbaa＆Wood[16]、Aiban＆Znidarcic[17]和Pane＆Schiffman[18]通过试验证实了该模型能较好地描述孔隙比与渗透系数的关系。

本文采用这一非线性渗透模型，为了方便与lge-lgp进行联合推导方程，将方程改写为：

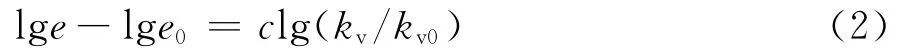
式中：c称为修正渗透系数。

1.3 非线性固结控制方程的建立

实际中大部分的施工荷载都是分级施加，假设施工荷载q（t）＝pi（当ti＜t≤ti＋1，i＝1…m－1）；q（t）＝Q。由有效应力原理p＝p0＋q（t）－u，对t求偏导得：

由压缩方程式（1）得：

式中：St＝pc／p0为结构应力比。

式（4）两端分别对时间t求偏导，并联立式（1）、（2）得：上述各式中：e、p和kv分别为饱和土当前孔隙比、有效应力和渗透系数；e0、p0和kv0分别为饱和土初始孔隙比、初始有效应力和初始渗透系数；u为当前饱和土的超静孔隙水压力；q（t）为当前施工荷载；γw为水重度。

小应变条件下饱和软土一维固结方程为：

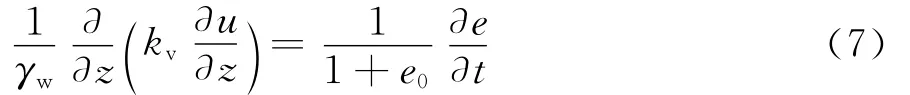
将式（4）、（5）、（6）代入式（7），可得考虑结构应力比与分级加载影响的一维非线性固结方程：

边界条件和初始条件为：

u＝0（t＝t1＝0，0≤z≤H，H为土层厚度）

z＝0 u＝0

1.4 固结方程的差分法求解

方程（8）为二阶非线性偏微分方程，本文采用Crank-Nicolson有限差分法来求解该偏微分方程。

对p＝p0＋q（t）－u两边关于z求导得：∂u／∂z＝γ′－∂p／∂z，则方程（8）可改写为：

由有效应力原理，故初始条件和边界条件也相应变为：

p＝p0（t＝t1＝0，0≤z≤H，H为土层厚度）

z＝0p＝p0＋q（t）

z＝ H∂p／∂z＝γ′（底面不排水）或

p＝p0＋q（t）（底面排水）

方程（10）的差分格式为：

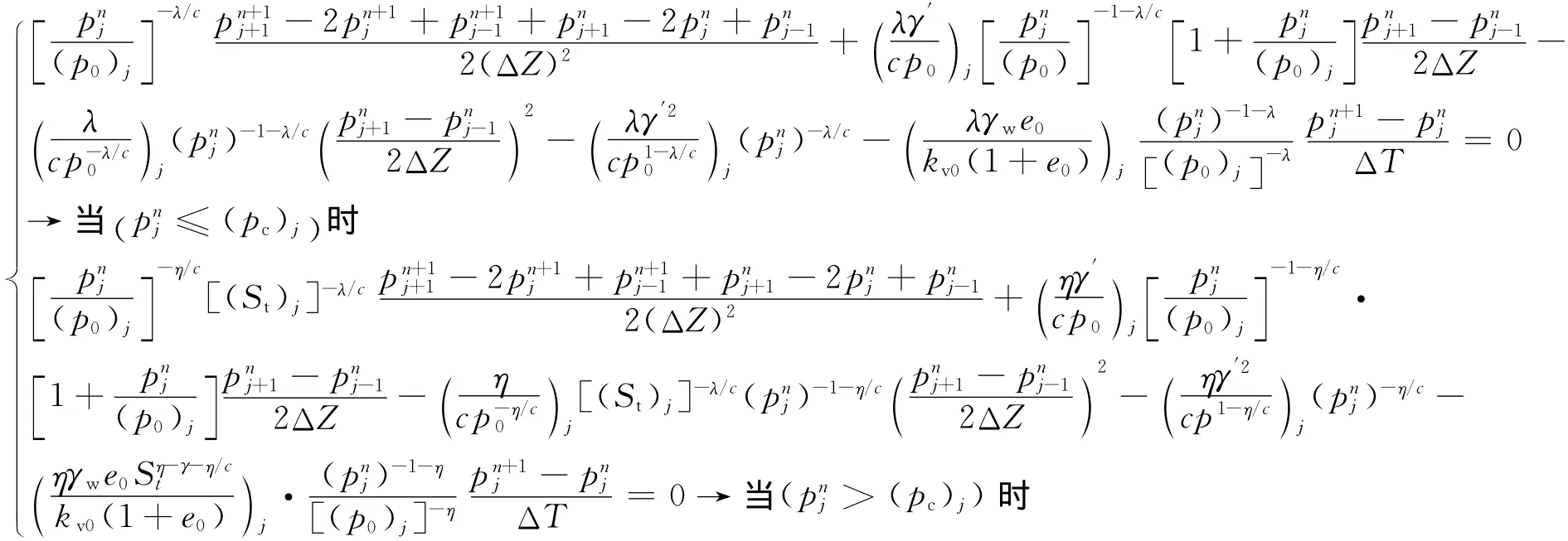
式中：ΔZ为空间步长；ΔT为时间步长；j代表空间节点数，j＝1，2，3，…m，其中m为土层离散结点总数；n代表时间节点数，n＝1，2，3，…。如令：

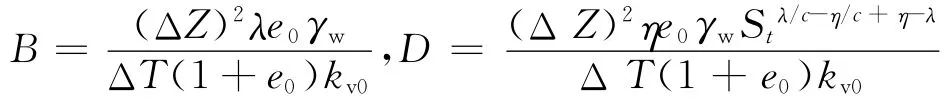
则上式整理后用一个通式表示为：

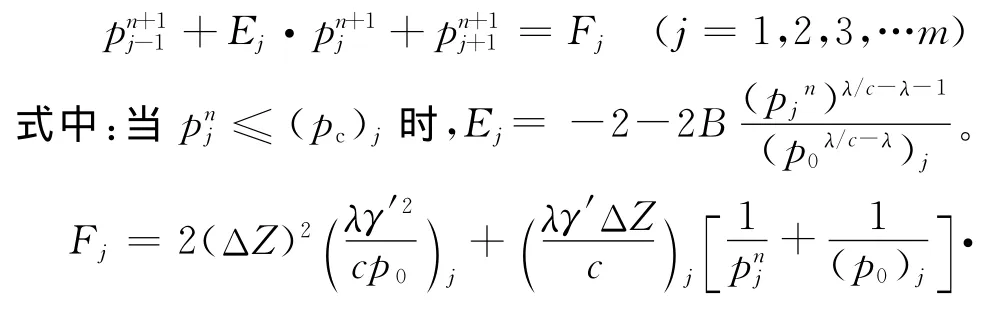
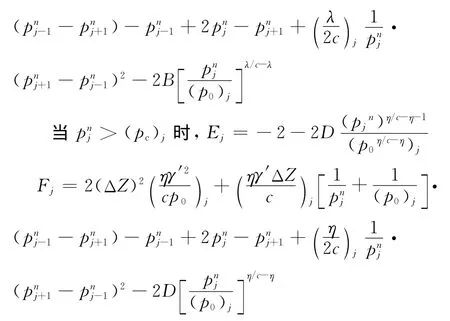
上式亦可用矩阵形式表示：

双面排水时，E矩阵中元素2变为0，P、F表达式同前，同理Ej，Fj（j＝2，3，…m－1）亦如前，E1＝1，Em＝1，F1＝，Fm＝。

矩阵方程中关于未知数都是线性的，因此根据初始条件可以使用追赶法来求解。土层平均固结度采用谢康和等[19]建议的按孔压定义的计算平均固结度公式，即：

式中：Up为土层平均固结度；q（t）为计算时刻的施工荷载；qu为施工结束后的荷载；uj（t）为计算时刻某深度点的孔压。

根据上述算法，编制了相应的C＋＋＆MFC计算程序来求解一维非线性固结问题。

2 考虑结构应力比的非线性固结算例

假设分级施工荷载变化如图2，固结参数如表1所示。差分计算假定空间步长取ΔZ＝0.05m，时间步长ΔT＝0.5d，修正渗透系数c＝0.14。

图2 分级施工荷载变化规律

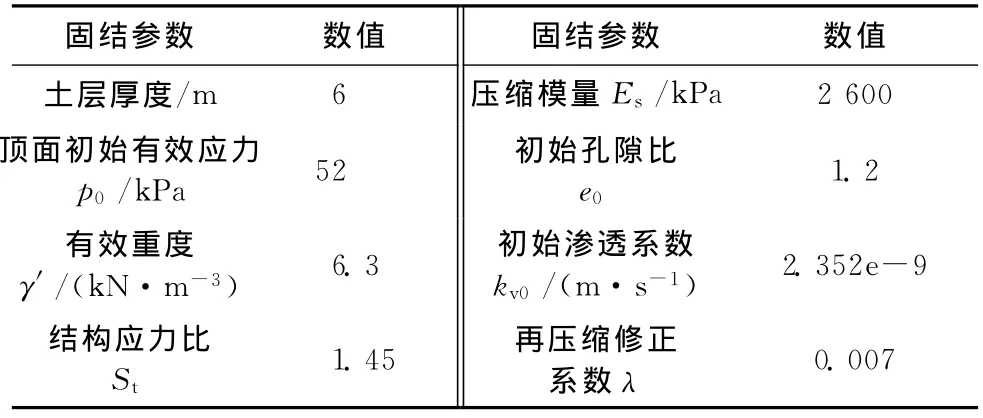
表1 固结有关参数

图3和图4分别为t＝150d时的孔隙水压力随深度变化曲线及固结度曲线。从图中可以看出，考虑结构应力比的超孔隙水压力远小于不考虑结构应力比的计算结果，且随深度的增加差值越来越大，而太沙基线性固结的计算结果则介于两者之间。这是由于土体结构性的存在，当有效固结应力小于土结构屈服应力时，土体压缩性较小，如果考虑了结构应力比，非线性固结分析得到的超孔隙水压力有较明显的消散，从而其固结度也要比不考虑结构应力比的非线性固结度大些。当有效固结应力大于土的结构屈服应力后，土体结构逐渐破坏，其孔压发展与固结曲线变化较复杂，下节将详细讨论。

图3 超孔隙水压力与深度关系曲线

3 与现场实测值的比较分析

实测资料来源于文献[20]，该工程位于深圳湾，土层为海相沉积软土，结构性强，土层的物理力学参数如表2所示。现场试验加载方式简化为分级加载，如图5所示。

图4 固结度与时间关系

加载过程5m深处的孔压和固结度实测值与本文的非线性固结计算程序计算的结果比较如图6和图7。从图中可以看出超孔隙水压力变化曲线和固结度与实测值的曲线比较接近，计算结果证明了本文方法的有效性。

图5 简化的分级施工荷载

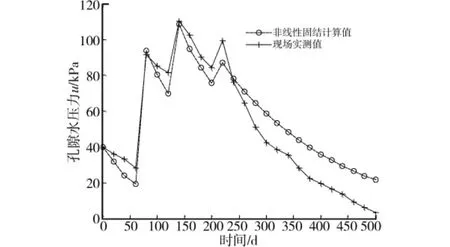
图6 5m处超孔隙水压力与时间关系

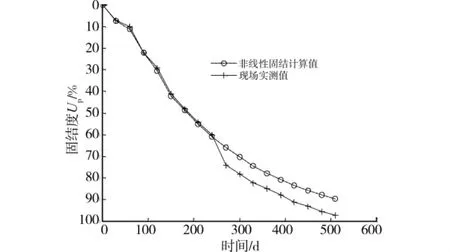
图7 固结度与时间关系

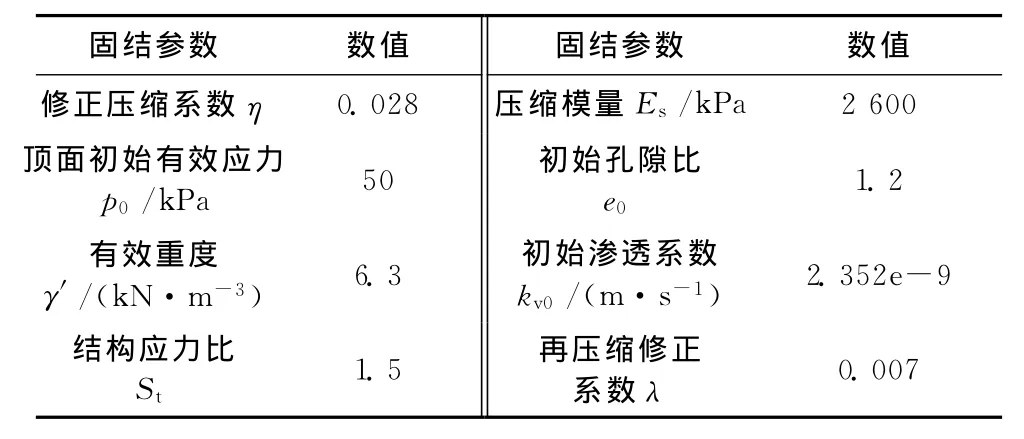
表2 土层参数表

4 非线性参数对计算结果的影响分析

4.1 η／c比值变化影响

在非线性固结分析中，η／c比值的不同必定会固结过程有影响，Berry ＆ Wilkinson[21]指出：η／c在0.5～2之间，而且大多在0.5～1之间。为了考虑η／c比值变化对土体固结的影响，取η／c从0.1～3.0进行分析。计算中固定c＝0.14，变化η来改变η／c比值，其中考虑结构应力比的非线性参数λ均取0.007，不考虑结构应力比的非线性参数取与η同值，线性固结参数不变以作为参考，其余参数同表1。限于篇幅，图8给出了η／c＝0.1、0.3、0.5、0.7、1.0、1.2、1.5、2.0等8种比值的超孔隙水压力－时间曲线以及固结度曲线。

从图中可以看出，η／c比值对非线性固结速率有较大影响，η／c越小，固结速率越快。

当η／c＜0.5时，不考虑结构应力比的固结曲线在线性固结与考虑结构应力比的固结曲线之间。比值较小时考虑与不考虑结构应力比的曲线差别不大，随着η／c比值的增加，非线性固结与线性固结差值逐渐减小，不考虑结构应力比的非线性固结曲线变化更快，逐渐接近线性固结曲线，特别是在固结初始阶段。

随着η／c比值的增加，不考虑结构应力比的非线性固结曲线越过线性固结曲线，考虑结构应力比的非线性固结与线性固结的差值逐渐减小，但在固结初始阶段二者仍有较大差别。随着η／c比值继续增加，二者出现交点，交点位置位于外荷载等于结构屈服应力处，η／c比值增加，交点位置基本不变。

固结初始阶段，在外荷载未达到土结构屈服应力之前，不考虑结构应力比的非线性固结由于未考虑粘土天然结构应力的存在而高估了土体非线性的影响，致使计算的超孔隙水压力偏大。太沙基线性固结既未考虑土的结构应力也未考虑土压缩与渗透的非线性，综合的结果是其固结曲线位于上述两者之间。

在外荷载超过土结构屈服应力之后，土天然结构逐渐破坏，但由于初始压缩阶段（未到达结构屈服应力之前）的差别，考虑与不考虑结构应力比的固结曲线并不重合，近似平行发展。太沙基线性固结因为忽略了固结后期孔隙比和渗透系数的降低而高估了固结速度，随着η／c比值的增加，非线性固结与线性固结曲线差值逐渐增加。

图8 不同η／c比值的超孔压－时间曲线及固结度曲线

4.2 进一步的讨论

上述分析是基于一组固定的参数（除η有变化）得出的结果，此外本文还进行了不同参数取值的固结分析。研究结果表明，对于不同参数固结曲线变化规律一致，但3种曲线变化相对位置的η／c界限值有差异。

就工程实践来说，η／c比值一般在0.5～1.2之间，考虑结构应力比的非线性固结最接近天然粘土的固结特性。当外荷载到达结构屈服应力之前，太沙基线性固结曲线接近考虑结构应力比的非线性固结曲线，可以近似使用。但当外荷载大于粘土的结构屈服应力之后，太沙基固结理论由于忽略了粘土固结的非线性而偏离实际情况较大。而不考虑结构应力比的非线性固结理论由于没有考虑固结初始阶段粘土结构性的影响而低估了粘土的固结速率，与实际也有较大偏差。

需要指出的是，本文并未考虑天然饱和软粘土的蠕变影响，文献[22]指出，在结构性软土固结过程中应考虑结构应力和蠕变的双重影响，否则会与实测结果偏差较大，并带来安全隐患。

5 结 论

建立了考虑结构应力比的饱和软粘土一维非线性固结控制方程，并采用有限差分法进行了求解，针对不同η／c比值分析了饱和软粘土的一维非线性固结性状，研究得出以下结论：

1）非线性参数η／c的取值对固结速率有较大影响，η／c值越小孔压消散越快，固结速率越大。

2）不考虑结构应力比的非线性固结与太沙基线性固结在固结初始阶段计算结果较接近，但随着固结的发展，不考虑结构应力比的非线性固结由于未考虑粘土天然结构应力的存在而高估了土体非线性的影响。

3）就工程实践来说，η／c比值一般在0.5～1.2之间，考虑结构应力比的非线性固结更接近天然粘土的固结性状，本文计算结果与实测值的比较也说明了这一点。

[1]DAVIS E H，RAYMOND.A non-linear theory of consolidation[J].Geotechnique，1965，15（2）：161-173.

[2]MESRI G，CHOI Y K.Settlement analysis of embankments on soft clay[J]. Journal of the Geotechnical Engineering Division，ASCE，1985，111（4）：441-464.

[3]BARDEN L，BERRY P L.Consolidation of normally consolidation clay[J].Journal of the Soil Mechanics and Foundation Division，ASCE，1965，91（5）：15-35.

[4]XIE K H，XIE X Y，JIANG W.A study on one dimensional nonlinear consolidation of double-layered soil[J].Computers and Geotechnics，2002，29（2）：151-168.

[5]XIE K H，LEO C J.A study on one dimensional nonlinear consolidation of soft soils[R].School of Civic Engineering and Environment，UWS，Nepean，Australia，1999.

[6]曹宇春，陈云敏，黄茂松.任意施工荷载作用下天然结构性软粘土的一维非线性固结分析 [J].岩土工程学报，2006，28（5）：569-274.CAO YU-CHUN， CHEN YUN-MIN， HUANG MAOSONG.One-dimensional nonlinear consolidation analysis of structured natural soft clay subjected to arbitrarily time-dependent construction loading[J].Chinese Journal of Geotechnical Engineering，2006，28（5）：569-274.

[7]吴建，谢新宇，朱向荣.饱和土体一维复杂非线性固结特性研究 [J].岩土力学，2010，31（1）：615-620.WU JIAN，XIE XIN-YU，ZHU XIANG-RONG.Study of properties of 1-D complex nonlinear consolidation of saturated soils[J].Rock and Soil Mechanics，2010，31（1）：615-620.

[8]MENÉNDEZ C，NIETO P J G，ORTEGA F A，et al.Non-linear analysis of the consolidation of an elastic saturated soil with incompressible fluid and variable permeability by FEM [J]. Applied Mathematics and Computation，2010，216：458-476.

[9]王俊，雷宏武，徐芬，等.变渗透系数软土一维非线性固结沉降数值模拟 [J].地下水，2010，32（2）：155-157.WANG JUN，LEI HONG-WU，XU FEN，et al.Numerical simulation of soft soil no-linear consolidation settlement with variable hydraulic conductivity[J].Ground Water，2010，32（2）：155-157.

[10]商卫东，白冰.荷载随时间变化情况下非线性固结问题的求解方法 [J].水利与建筑工程学报，2010，8（1）：27-29.SHANG WEI-DONG，BAI BING.Analytical methods for nonlinear consolidation of saturated soils under time-dependent loading[J].Journal of Water Resources and Architectural Engineering，2010，8（1）：27-29.

[11]邓岳保，谢康和.互补算法在一维非线性固结求解中的应用 [J].岩土力学，2011，32（9）：2656-2662.DENG YUE-BAO，XIE KANG-HE.Application of complementary algorithm for solving one-dimensional nonlinear consolidation[J].Rock and Soil Mechanics，2010，2011，32（9）：2656-2662.

[12]沈珠江.软土工程特性和软土地基设计 [J].岩土工程学报，1998，20（1）：100-111.SHEN ZHU-JIANG.Engineering properties of soft soils and de sign of soft ground[J].Chinese Journal of Geotechnical Engineering，1998，20（1）：100-111.

[13]刘恩龙，沈珠江.结构性土压缩曲线的数学模拟[J].岩土力学，2006，27（4）：615-620.LIU EN-LONG， SHEN ZHU-JIANG. Modeling compression of structured soils[J].Rock and Soil Mechanics，2006，27（4）：615-620.

[14]CHAI J C，MIURA N，ZHU H H，et al.Compression and consolidation characteristics of structured natural clay[J].Canadian Geotechnical Journal，2004，41（6）：1250-1258.

[15]MESRI G，OLSON R E.Mechanisms controlling the permeability of clays[J].Clay and Clay Mineral，1971，19（3）：151-158.

[16]AL-TABBAA A，WOOD D M.Some measurements of the permeability of Kao-Lin[J].Getotechnique，1987，37（4）：499-503.

[17]AIBAN S A，ZNIDARCIC D.Evaluation of the flow pump and constant head techniques for permeability measurements[J].Geotechnique，1989，39（4）：655-666.

[18]PANE V，SCHIFFMAN R L.A note on sedimentation and consolidation[J].Geotechnique，1985，35（1）：69-72.

[19]谢康和，李冰河，郑辉，等.变荷载下成层地基一维非线性固结分析 [J].浙江大学学报：工学版，2003，37（4）：426-431.XIE KANGHE，LI BINGHE，ZHENG HUI，et al.Analysis of one dimensional nonlinear consolidation of layered soils under time-dependent loading[J].Journal of Zhejiang University：Engineering Science，2003，37（4）：426-431.

[20]房后国.深圳湾结构性淤泥土固结机理及模型研究[D].长春：吉林大学，2005.

[21]BERRY P L， WILKINSON W B. The radial consolidation of clay soils[J].Geotechnique，1969，19（2）：253-284.

[22]NASH D F T.RYDE S J.Modeling consolidation accelerated by vertical drains in soils subject to creep[J].Géotechnique，2001，51（3）：257-273.