黏土的一维非平行等效时间线流变模型
胡亚元
(浙江大学a.岩土工程研究所;b.软弱土与环境土工教育部重点实验室,杭州 310027)
软土的受荷变形特性研究是岩土工程领域的主要研究课题之一,许多岩土力学专家对此进行了深入分 析[1-10]。张先伟和王常明[1]、薛新华和张我华[2]研究了软土的结构损伤特性。Crawford根据压缩流变试验绘制了正常固结土不同历时的e-lgp曲线[4],Bjerrum 建立了 黏土流变 的等时 间线模型[5];Lerouel等提出了一维等应变率模型[6]。Yin& Graham[7],Yin等[8]建立了一维等效时间线流变模型,即Yin-Graham弹黏塑性模型(Elastic viscoplastic model,简称EVP model)。胡亚元依据超塑性理论(也称岩土耗散本构理论)论证了Yin-Graham一维等效时间线模型本质上是准塑性的黏弹性模型[12]。余湘娟和殷宗泽整理黏土蠕变试验结果后发现[13-14],荷载对正常固结土的次固结系数有明显影响,正常固结土不同等效时间线之间一般为不平行直线。然而,殷建华和Graham在建立一维等效时间线流变模型时,假定不同等效时间线为相互平行的直线[7-8]。显然,殷建华和Graham一维等效时间线流变模型无法反映不平行等效时间线的流变性质,对于等效时间线不平行时的一维流变模型,据笔者所知,文献还未报导,有必要对其进行研究。
笔者首先在连续介质流变理论框架下进一步分析殷建华和Graham所提出的等效时间的物理内涵,建立等效时间与不可逆流变速率之间的数学物理关系,揭示等效时间本构模型的建模思路是采用根据简单加荷历史求得的流变速率去建立能适应复杂加荷历史的流变模型,从而把殷建华和Graham所提出的等效时间的物理内涵统一在连续介质流变理论的框架之内。然后根据等效时间线不平行时的性质以及等效时间与流变速率之间的关系获得等效时间线不平行时流变速率的计算公式,进而获得等效时间线不平行时黏土的一维流变微分本构方程。文后算例把非平行等效时间线流变本构模型在骤然施加恒载条件下所获得的理论结果与室内试验数据[13]进行了对比,结果表明两者较吻合,说明本文的流变模型是合理的。
1 流变速率与等效时间之间的关系分析
建立等效时间流变模型,首先需要在连续介质的框架内确定流变速率与等效时间物理内涵的内在联系。借鉴殷建华和Graham的研究成果,本文也采用弹簧和黏性均为非线性的Maxswell黏弹性力学元件来模拟黏土的一维流变性质[7]。Maxswell黏弹性力学元件图为:
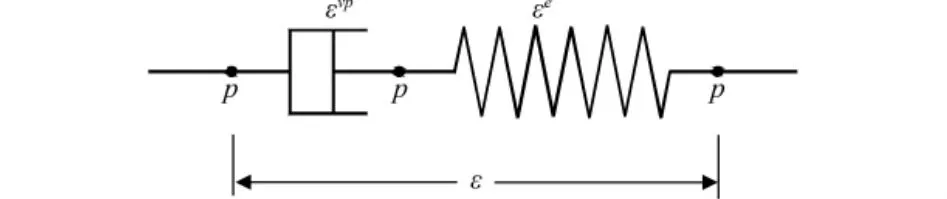
图1 殷建华-Graham EVP模型的力学元件组合
根据图1有:

一维条件下弹性应变与应力的一般关系为:

式中的p为有效应力,对于一维竖向压缩情况其为竖向有效应力,对于一维等向压缩情况其为有效应力张量的球应力。根据连续介质理论,一维条件下流变速率的一般形式可表示为

在本文中,加荷历史指的是应力或应变随时间增加或减少的不同加荷方式;加荷路径指的是应力或应变在其空间中具体的变化迹线。式(3)表达式实际暗含了以下假定:“黏土的流变速率只与应变ε和应力p有关,而与到达该应变量ε和应力p的加荷历史无关”。即对于不同的加荷历史,到达特定应变量ε和应力p时的流变速率是一致的。这一性质告诉我们,在实际黏土力学试验中,可以把从简单加荷历史中求得的流变速率规律用到复杂加荷历史的建模工作中去。
对于岩土材料而言,由于其流变速率的本构关系较为复杂,因此根据岩土试验直接测定流变速率随应变量和有效应力的变化关系较为困难,而测定应变随时间的变化规律则相对较为容易。因此在岩土试验中一般先测定应变随时间的变化规律,再根据应变随时间的变化曲线反算流变速率。设岩土试验中测定应变随时间的变化曲线时选定的应力加荷历史为:

式中的s为应力历史选择因子,对于一条具体的应力加荷历史而言s值是恒定的;当s变化时,可以形成建模所需的其它应力加荷历史。把式(4)代入到式(3)后再代入到式(1)得:
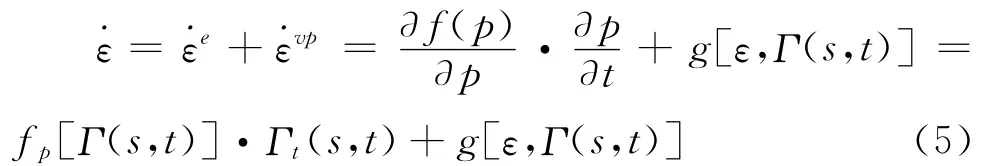
式(5)中函数对变量的偏微分函数采用了函数下标是其变量的标记方式来表示。显然,对于一条具体的应力历史s恒定,式(5)是一个一元微分方程,对于t=0时的初始应变值ε0=ε0(s),根据一元微分方程理论可知式(5)必存在解,其形式可表示为[15]:

式(6)表明,应变ε、应力历史选择因子s和时间t具有唯一关系。
现采用应变ε和应力p作为坐标构成一个面N(p,ε),则由式(3)可知流变速率是N(p,ε)面上的一个函数。而由式(4)和式(6)又可知,当应力历史选择因子s和t=0时的初始应变值ε0=ε0(s)恒定时,根据式(4)所确定的应力p和根据式(6)所确定的应变ε组成的点 (p,ε)在N(p,ε)面上形成了一条随时间变化的曲线。当s变化时,该曲线在N(p,ε)面上也随着发生移动,从而在N(p,ε)面的某个区域内形成一个面R(p,ε)。显然有R(p,ε)⊆N(p,ε),把面R(p,ε)称为应力应变关系面,简称本构面R(p,ε)。
从另一视角能更深入地理解本构面R(p,ε)在反算流变速率中所具有的重要作用。由式(4)可知,选择不同的s可以形成不同的应力随时间变化曲线即不同的应力加荷历史,因此通过改变s可以形成一个应力历史簇 〈p〉,记为:〈p〉= 〈p =Γ(s,t),s∈可选择域〉,根据该应力历史簇〈p〉中的每一条具体的应力历史,由式(6)可求得相应的应变历史线,从而形成与应力历史簇〈p〉相对应的应变随时间的变化曲线簇 〈ε〉,简称应变历史簇 〈ε〉,即:〈ε〉=[ε=Η[s,t,ε0(s)],s∈ 可选择域]。显然,根据应力历史簇〈p〉和与之相对应的应变历史簇〈ε〉可构成一个坐标为 (p,ε)的面,即为上文所简称的本构面R(p,ε),现在我们来证明,当函数ε=Η[s,t,ε0(s)]和p=Γ(s,t)关于自变量s和t的Jacobian行列式的值不为零时,根据应力历史簇〈p〉和应变历史簇〈ε〉可以反推流变速率关系式式(3)。推导过程如下:
根据应变随时间变化线簇ε=Η[s,t,ε0(s)]可得:

根据应力历史簇特性p=Γ(s,t)又有:

根据式(1)有:
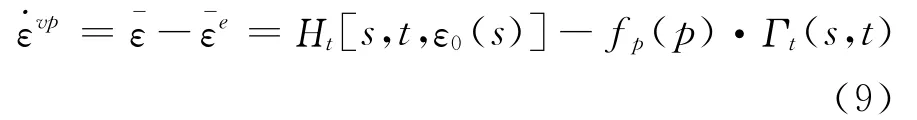
同时,根据多元函数论可知,当函数ε=Η[s,t,ε0(s)]和p=Γ(s,t)关于自变量s和t的Jacobian行列式值不为零时,则存在唯一反函数Ω(ε,p)和Ξ(ε,p)[16],使得:
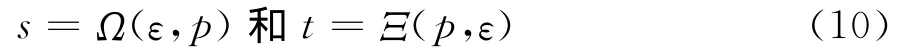
把式(9)中的s和t用式(10)代替就可以求得式(3)。式(9)和式(10)表明,当应力历史簇 〈p〉和与之相对应的应变历史簇 〈ε〉构成的本构面R(p,ε)穷尽实际可能的一切本构点时,那么根据应力历史簇〈p〉和与之相对应的应变历史簇〈ε〉可求得实际需要的任意本构点的流变速率。
值得注意的是〈p〉虽然是一个应力历史簇,但该应力历史簇却未包括所有的应力历史。如黏土蠕变试验常用的恒载簇〈p〉=〈p=s,s∈可选择域〉,式中s一旦选定即为不随时间变化的常数,它显然无法包含类似p=s+at这样的应力历史的。不过,虽然力学试验所选定的应力历史簇〈p〉不能包含实际可能的其它应力历史,但不同应力历史间的流变速率与应力历史无关,因此根据应力历史簇〈p〉及其相应的应变历史簇〈ε〉所求得的流变速率,却可以用以建立适用于其它任何应力历史的流变本构模型。因此可见,当根据土工试验直接总结流变速率关系式式(3)存在困难时,可以采用应力历史簇〈p〉和与其相应的由土工试验测定的应变历史簇〈ε〉反算流变速率并由此间接建立岩土的流变模型。
众所周知,应变随时间的变化规律与应力历史密切相关,对流变模型而言与应力历史无关的是流变速率而不是实际时间,因此应力和应变历史簇中的时间t并不同于其他一般应力历史的时间t,一般应力历史的时间t与应力历史簇间的时间t之间的关系只能通过流变速率式(3)建立联系,而应力和应变历史簇中的时间t的作用仅是计算流变速率式(3)。如果把应力历史簇 〈p〉和应变历史簇 〈ε〉中计算流变速率所用的时间和一般应力历史条件下的持续时间均采用相同符号t来表示就会相互混淆。为区别这两个时间,考虑到时间在应力历史簇 〈p〉和应变历史簇〈ε〉中的作用是计算流变速率,同时也强调应力历史簇〈p〉和应变历史簇〈ε〉在计算流变速率时的重要性,在下文中,笔者把应力历史簇〈p〉和应变历史簇〈ε〉所涉及的时间t用大写的Te来表示,并把Te称为应力历史簇 〈p〉在初始时刻ε(Te=0)=ε0(s)下的等效时间,把初始时刻线ε(Te=0)=ε0(s)称为参考等效时间线。如果等效时间的大小与所选择的参考等效时间线无关,则把该等效时间称为绝对等效时间,并把它记为T[12]。显然,根据等效时间的定义,当实际应力历史属于应力历史簇〈p〉和初始时刻线为参考等效时间线时,有

当〈p〉为恒载簇〈p=s,s∈ 可选择域〉时;由于p=s,参考等效时间线表达式中的s用p替换后可写为ε(Te=0)=ε0(p),其式即为Yin-Graham一维EVP模型中压缩线表达式ε=+(λ/υ)ln(p/p0)的推广[4];此时应变历史簇 〈ε〉也可用p表示为ε=Η[p,Te,ε0(p)],它是Yin-Graham一维EVP模型中应力、应变和等效时间唯一关系表示式(见文献[7]中的式(4))的推广。由此可见,本文等效时间及其参考等效时间线的定义包含了殷建华和Graham对等效时间及其参考等效时间线的定义,殷建华和Graham流变模型中的等效时间及其参考等效时间线是本文的特殊形式。
2 恒载簇作用下黏土流变的不平行等效时间线体系
土工试验常采用恒载簇〈p=s〉来研究黏土的流变特性,当s选择不同数值时形成了不同恒载作用下的流变试验。由于恒载簇中的应力历史满足p=s,故下文为行文简便直接用p来代替s。Crawford[4]和余湘娟等[13-14]根据土工实验证明,黏土流变的等效时间线是相互不平行的直线。现在利用这一性质来推导函数ε=Η[p,Te,ε0(p)]的具体形式。
等效时间线不平行时的示意图见图2,把恒载作用下流变试验中正常固结黏土蠕变变形时间为T0时的总应变随应力变化线作为等效时间Te=0的参考等效时间线ε(Te=0)=ε0(p),把p0作为参考应力,把p0在参考等效时间线上所对应的应变ε0作为参考应变,令:υ=1+et0为比容,et0为土体的初始孔隙比。根据图2中Te=0时的参考等效时间压缩线,A点的应变为:

式中的λ0为参考等效时间压缩线上的压缩系数。
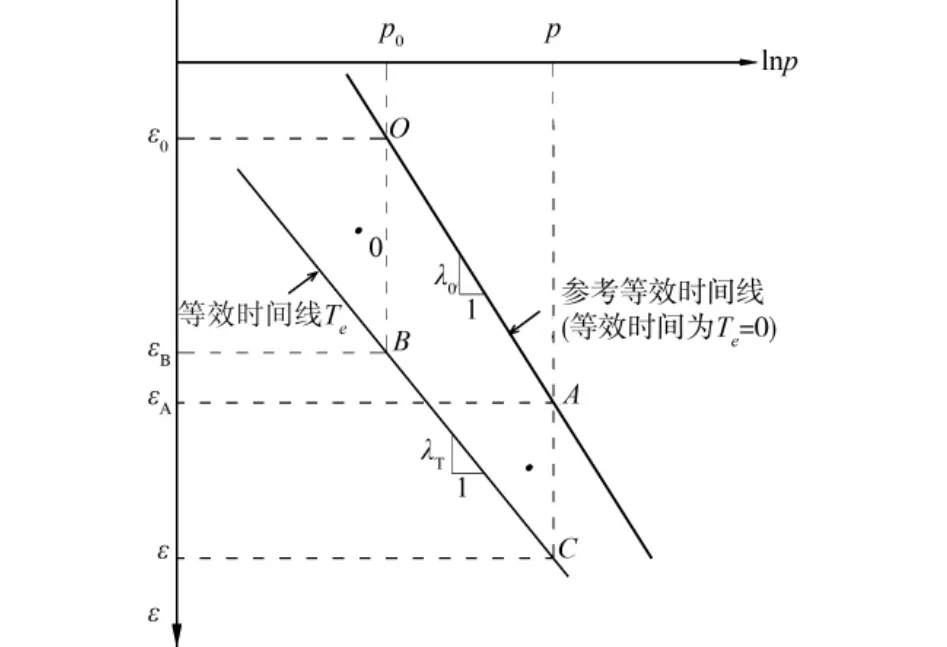
图2 黏土流变的等效时间线体系
根据恒载p0条件下的流变试验,B点的应变为:
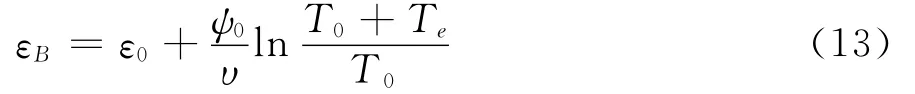
式中的ψ0为参考应力p0条件下的蠕变系数。根据Te=0时的参考时间压缩线和恒载p条件下的流变试验,C点的应变为:
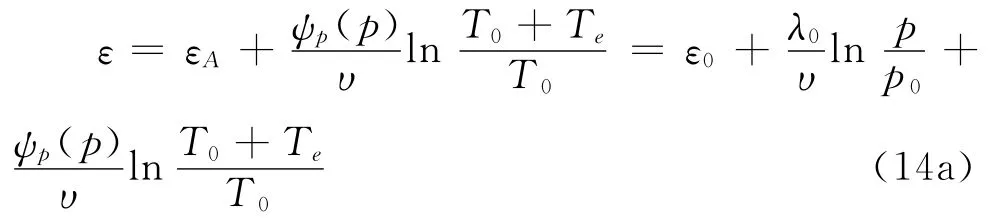
式中的ψp(p)为恒载p条件下的蠕变系数。另根据恒载p0条件下的流变试验和等效时间Te压缩线,C点的应变又有:

式中的λT(Te)为等效时间Te压缩线上的压缩系数。根据应力、应变和等效时间具有唯一性的性质,式(14a)和式(14b)计算的应变应相等,由此得:

注意到λT是关于等效时间Te的函数而ψp是关于应力p的函数,因此式(15)中等式左边仅是等效时间的函数,等式右边仅是应力p的函数,故该等式只有左右是常数才有可能成立,令该常数为ζ,有:

式中的常数ζ反映了压缩指数随等效时间和蠕变系数随应力的变化规律,由式(16)可得:

把式(17a)代入到式(14b)或把式(17b)代入到式(14a)均可得:

在推导式(19)时并未对C点作任何限定,因此式(19)对于任意的应力p和等效时间Te均成立,故式(19)是ε=Η[p,Te,ε0(p)]当黏土等效时间线不平行时的具体函数表达式。注意到当应力历史属于应力历史簇时式(11)成立,故根据式(9)由式(18)和式(11)得:
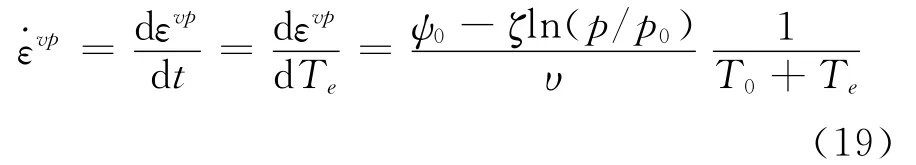
同时根据式(18)又可得:

把式(19)代入到式(20)得:
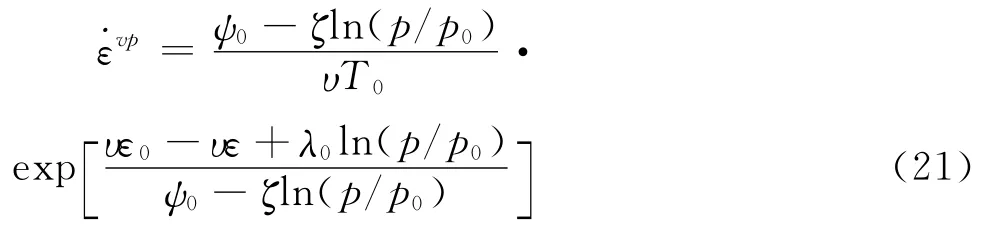
尽管式(21)是基于特定的应力历史簇〈p〉获得的,但根据式(3)流变速率只与应力p和应变ε有关而与应力历史无关的性质,故它可以用于其它任意应力历史所涉及的流变速率计算。
黏土的弹性应力应变关系可表示为:

式中的κ为回弹指数,由式(22)可得:

把式(21)和式(23)代入式(1)有:
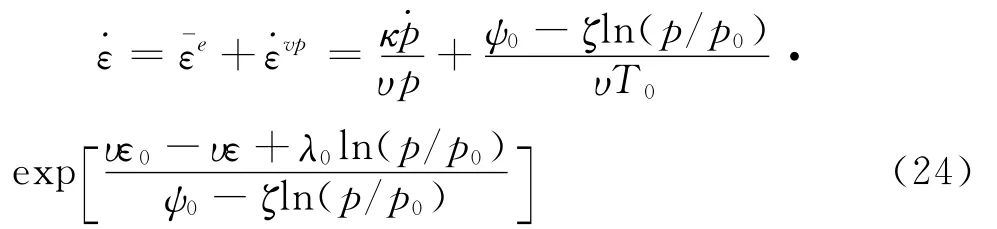
式(24)即是等效时间线不平行时的准塑性黏弹性本构方程。
根据物理意义可知,当ζ=0时非平行等效时间线退化为平行等效时间线。本文的本构方程将退化为Yin-Graham一维流变模型。把ζ=0代入到式(24)得:
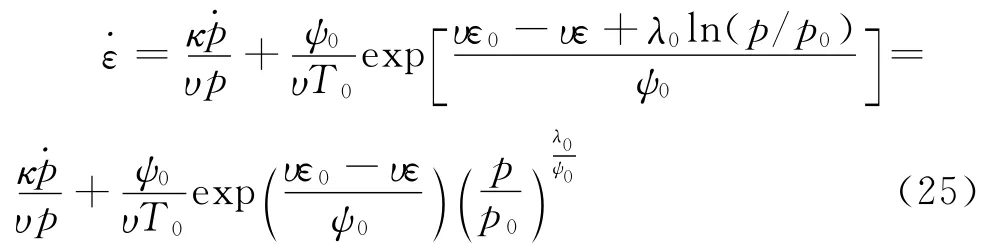
除采用不同的符号表示物理参数外,式(25)与Yin-Graham一维流变模型相同,这说明推导是正确的。
与Yin-Graham 一维流变模型相类似[6],如令:

则式(13)—(18)中的T0+Te可用T 来代替。式(18)是反映等效时间线ε=Η[p,Te,ε0(p)]的函数表达式,把式(18)中的T0+Te用T来代替后得:
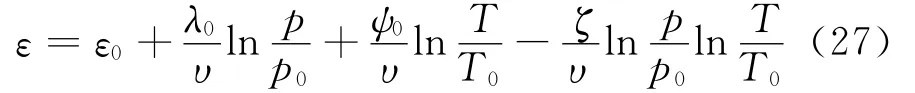
先把式(26)代入到式(17a)和式(17b)后,再根据式(27)、式(17a)和式(17b)得:
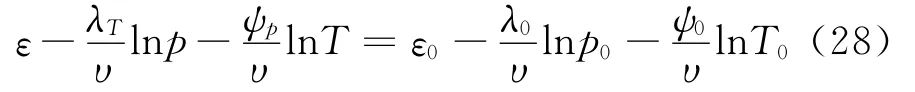
式(28)表明,任何一条等效时间线的T值大小与T0值的选择无关[12,18],即与选择哪一条等效时间线为参考等效时间线无关,因此T为绝对等效时间。
在土工试验室内常用孔隙比来代替应变量,故采用e=e0-υ(ε-ε0)把式(27)和(24)变换得:

设t=0时软土的初始孔隙比为e=et0,初始有效应力为p=pt0。当土体骤然施加附加有效应力pf即当p=pt0骤然增加到pA=pt0+pf时,根据式(30)可求得孔隙比随时间的变化曲线为:
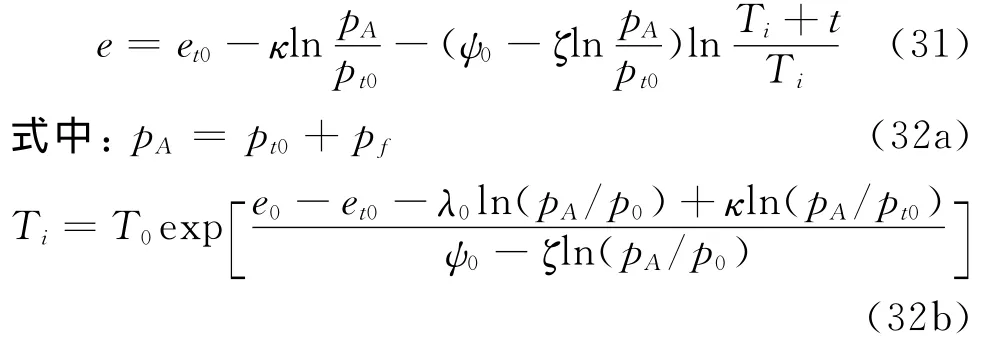
3 模型参数的确定及验证
余湘娟等采用室内试验研究了汕揭高速公路工程中软土的压缩流变特性[13]。根据其试验数据[13]绘制的恒有效应力为100kPa、200kPa、400kPa和1200kPa的应变随时间变化曲线如图3所示,他们发现软土的蠕变系数与软土压力有关,软土的等效时间线一般是不平行线。笔者将根据它们的试验数据来确定模型参数;同时,当有效应力骤然加载到800kPa和1600kPa时,其应变随时间的变化曲线如图6所示。笔者将用它们的试验数据与根据式(31)计算的理论预测值相对比,以验证本文本构模型的合理性。
根据图3的试验数据,图4给出了不同等效时间的e-lgp曲线,从图中可以看出,不同等效时间的e-lgp曲线是不平行的。这些e-lgp曲线的压缩指数随绝对等效时间的变化图如图5所示。根据本文第一节“流变速率与等效时间之间的关系分析”中的理论研究,建立流变速率与等效时间的定量关系时需要选择一个参考等效时间线。理论上,任意一条等效时间线均可以作为参考时间线。但在土力学中,室内土工参数一般按照室内试验历时1.0d来测定的,因此,本文选绝对等效时间T=1.0d线为参考绝对等效时间T0线,故T0=1.0d;同理,任何一个压力均可以取为参考有效压力,但鉴于在经典土力学中,根据100kPa至200kPa引起的孔隙比变化量来计算土体的压缩系数,故本文选p0=100kPa为参考有效应力,据图3e-lgt曲线可知p0=100kPa时的蠕变系数为ψ0=0.01387;根据试验数据可得p0=100kPa在参考绝对等效时间T0=1.0d线所对应的参考孔隙比为e0=2.151,压缩指数为λ0=0.3737。根据图5和式(17a)可知ζ=0.0038,为阅读方便,把上述模型参数列于表1。

表1 以T0=1.0d线为基准的模型计算参数

图3 各级恒有效应力作用下e-lgt试验曲线[8]

图4 不同等效时间线的e-lgp关系曲线
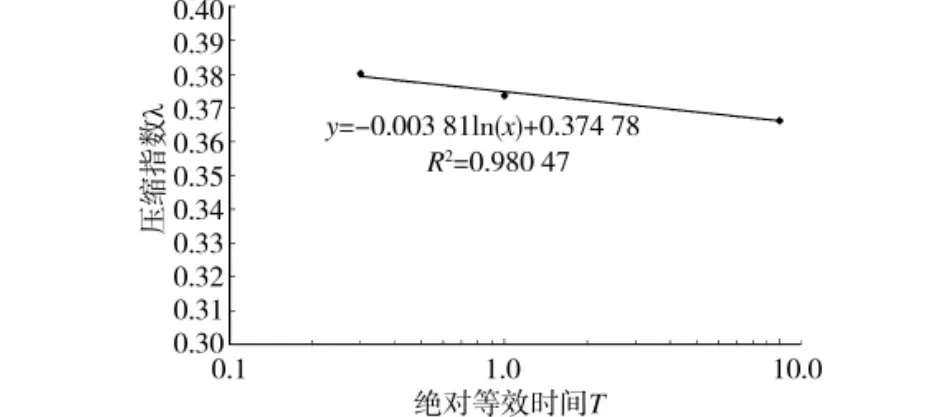
图5 压缩指数λ随绝对等效时间变化图
根据表1参数和式(31)得到的理论计算结果与试验数据对比图如图6所示,从图6可以看出,试验结果和理论预测值较为接近,说明该文建立的非平行等效时间线流变模型较合理地反映了软土的流变特性。
从表1还可以看出,ζ=0.0038。当等效时间历时较短时,压缩指数随等效时间变化的影响较小,但由于民用建筑的设计年限为50a,高速铁路路基的设计年限为100a,据式(17a)知在此期间软土的压缩指数数值减少了Δλ=0.038,约占λ0的10%,同时,当土压力从p=100kPa变化到p=1200kPa时,据式(17b)知蠕变系数减少了Δψ=0.0095,约占ψ0的68%,说明当等效时间较长和土压力变化较大时,一般不能忽略非平行等效时间线特性对压缩指数特别是蠕变系数的影响。
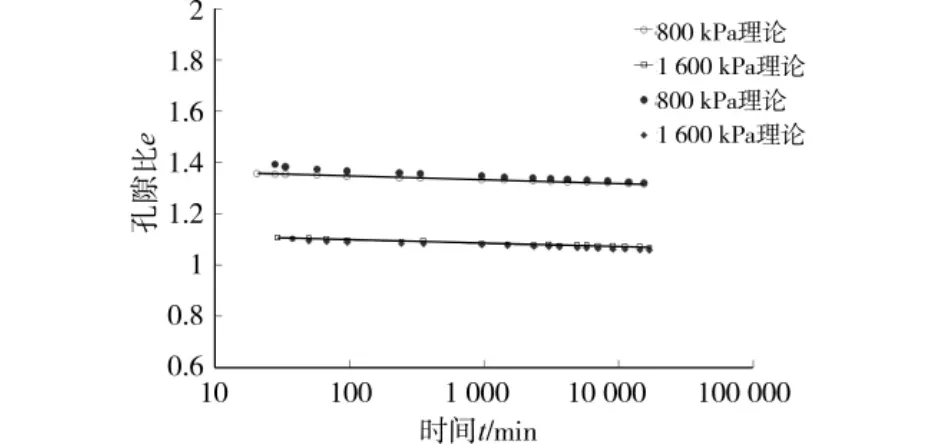
图6 骤然加载到800kPa和1600kPa时试验数据与理论预测值对比图
值得指出的是,在等效时间线不平行的情况下,当选择不同等效时间和不同有效压力作为参考等效时间和参考有效压力时,相应的ψ0、λ0和e0在数值上会发生变化,但这些ψ0、λ0和e0之间在数值上服从公式式(17a)、(17b)和式(18),故依据这些ψ0、λ0和e0建立的等效时间流变模型可以按照公式式(17a)、(17b)和式(18)相互转化,故尽管它们的数值不同,但它们反映的等效时间流变性质是相同的,它们体现的是相同的等效时间流变模型。同时,与经典土力学一样,在均质试样中,试样厚度对ψ0、λ0和e0的取值无影响。
4 结 论
从连续介质流变理论出发,研究了等效时间与流变速率之间的内在联系,并建立了等效时间线不平行时黏土的一维准塑性的黏弹性模型,获得了以下研究成果:
1)在非线性流变模型中,当流变速率只与应变量和应力有关时,可以把简单加荷历史获得的流变速率用于复杂加荷历史地建模工作。等效时间的物理内涵是简单加荷历史簇中反算流变速率所采用的持续时间。
2)利用等效时间的物理内涵,建立了黏土非平行等效时间线的一维流变模型。该模型能够退化为等效时间线平行时的Yin-Graham一维流变模型。根据余湘娟等试验数据确定了模型参数,并用与确定模型参数无关的另二组试验数据对理论预测值进行了对比,试验结果与理论预测值较为吻合,验证了模型的合理性。
[1]张先伟,王常明.软土结构性定量化参数研究[J].土木建筑与环境工程,2010,32(4):38-43,48.ZHANG XIAN-WEI, WANG CHANG-MIN.Quantitative para-metric analysis of soft clay structure[J].Journal of Civil,Architectural & Environmental Engineering,2010,32(4):38-43,48.
[2]薛新华,张我华.考虑损伤的软土路基变形分析 [J].土木建筑与环境工程,2009,31(1):77-82.XUE XIN-HUA,ZHANG WO-HUA.Deformation of soft ground with consideration of the concomitant damage[J]. Journal of Civil, Architectural &Environmental Engineering,2009,31(1):77-82.
[3]牟春梅,李佰锋.外荷载作用下软土压缩模量动态演化规律 [J].土木建筑与环境工程,2009,31(4):49-54.MU CHUN-MEI,LI BAI-FEN.Dynamic evolution pattern of compression modulus of soft clay[J].Journal of Civil, Architectural & Environmental Engineering,2009,31(4):49-54.
[4]CRAWFORD C B.Interpretation of consolidation tests[J]. Journal of Soil Mechanics and Foundation Division,ASCE,1964,90(5):87-102.
[5]BJERRUM L. Engineering geology of Norwegian normally consolidated marine clay as related to the settlements of buildings[J].Geotechnique,1967,17(2):83-118.
[6]LEROUEIL S,MARQUES M,TAVENAS F,et al.Stress-strain-strain rate relation for the compressibility of natural sensitive clay[J].Geotechnique,1985,35(2):159-180.
[7]YIN J H,GRAHAM J.Equivalent times and onedimensional time-dependent behavior of clays [J].Canadian Geotechnical Journal,1994,31:42-52.
[8]YIN J H,ZHU J G,GRAHAM J.A new elastic viscoplastic model for time-dependent behavior of normally and overconsolidated clays:theory and verification[J].Canada Geotechnical Journal,2002,39:157-174.
[9]HINCHBERGER S D,QU G.Viscoplastic constitutive approach for rate-sensitive structured clays[J].Canada Geotechnical Journal,2009,46:609-626.
[10]KARIM M R,GNANENDRAN CT,LO S C R,et al.Predicting the long-term performance of a wide embankment on soft soil unsing an elastic-viscoplastic model[J].Canada Geotechnical Journal,2010,47:244-257.
[11]HOULSBY G T,PUZRIN A M.Principles of hyperplasticity[M].London,Springer,2006:211-239.
[12]胡亚元.准塑性的黏弹性模型在黏土中的应用[J].岩土工程学报,2009,31(3):353-360.HU YA-YUAN.Application of plastic-like visco-elastic model on clay[J].Chinese Journal of Geotechnical Engineering,2009,31(3):353-360.
[13]余湘娟,殷宗泽,董卫军.荷载对软土次固结影响的试验研究 [J].岩土工程学报,2007,29(6):913-915.YU XIANG-JUAN,YIN ZONG-ZE,DONG WEIJUN.Influence of load on secondary consolidation deformation of soft soils[J]. Chinese Journal of Geotechnical Engineering,2007,29(6):913-915.
[14]余湘娟,董卫国,殷宗泽.软土次固结系数与压力的关系[J].河海大学学报:自然科学版.2008,36(1):45-48.YU XIANG-JUAN,DONG WEI-JUN,YIN ZONGZE.Relationship between loads and secondary consolidation coefficients of soft clay soils[J].Journal of Huhai University:Natural Science,2008,36(1):45-48.
[15]蔡遂林.常微分方程[M].2版.武汉:武汉大学出版社.2003:80-128.
[16]ERINGEN A C.Microcontimuum field theories[M].Springer,Hong Kong,1999:5-8.
[17]殷宗泽,张海波,朱俊高,等.软土的次固结[J].岩土工程学报,2003,25(5):521-526.YIN ZONG-ZE,ZHANG HAI-BO,ZHU JUN-GAO,et al.Secondary consolidation of soft soils[J].Chinese Journal of Geotechnical Engineering,2003,25(5):521-526.
——基于平面应变条件

