分离刚度法测试杨木单板层积材木梁剪切模量的试验研究

卫佩行，王泉中，周定国

（1.南京林业大学 木材工业学院，南京 210037；2.南京林业大学 机械电子工程学院，南京 210037）

单板层积材（LVL）是旋切单板经过干燥、平行组坯压制的一种木质工程材料。通过这种方式可使单板缺陷分散，从而使来源于劣质木材的木质材料强度提高［1－2］。单板层积材一个显著优点是可设计性，通过加工，大的缺陷像节子及其它降低木材强度的缺陷会分散，从而得到一种更均质的产品［3－4］。由于单板层积性能相对均一，且尺寸不受限制，因此广泛用于结构部件，像楼梯扶手、门窗框架、木梁等等［2］。单板层积材可广泛应用。其第二个明显的优点是单板胶合使得小径木材制造大跨度木梁成为可能，能够使森林资源小材大用，劣材优用［2］。由于以上的优点，LVL是一种良好的工程材料.LVL来源于实体木材，但性能优于实木，多用于建筑与家具材料。

近十年来，加拿大、美国、日本都采用单板层积材作为包装材料。森林资源较丰富的加拿大和美国每年单板层积材的产量2×106m3以上，是中国产量的数十倍。中国单板层积材的研究和应用较少，不少外资企业从中国采购“单板层积材”等节材代木包装材料，用于机电产品包装。显而易见，中国破坏大量森林，采用实木而非单板层积材包装机电产品用于出口是相当不明智的［5］。

LVL用于承重材料，其力学性能至关重要。然后来源于木材的LVL正交各向异型材料，同时又是一个非均匀体。为了研究方便，也为了不完全失去其真实性，一般会做三个假设［6］。首先，假设木材是均匀的，根据这个假设，LVL被认为是一种均质材料，被研究的LVL没有节子、没有胞间道、且只包含边材。在宏观范围单板层积材力学性质既不是某一个宏观构造元素（如早材、晚材、大导管、射线束等可见组织）的个别特性，也不是旋切单板加工过程中产生的背面裂隙、表面粗糙度、厚度偏差等某一加工缺陷的集中反映，而是大量元素的平均性质，而且这些元素的尺寸都比试件宏观尺寸小得多，因此根据统计学理论，就能把LVL当成连续均匀介质对待。其次，假设LVL是一线弹性体，也就是在一定作用力下符合虎克定律。再次，假设LVL是各项异性的，选取L、T、Z为三个弹性主方向，它们的物理性质是不一样的，在假设前提下，可以认为它具有三个对称面（LT、LZ、TZ），也就是LVL是正交各向异性材料，具有9个弹性常数。其柔度常数在主轴空间的柔度矩阵为：

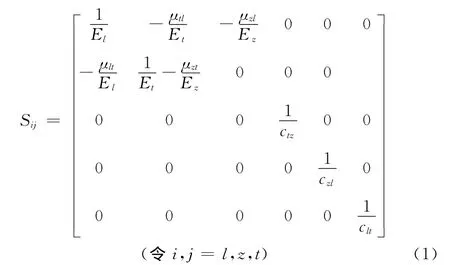
式中：Ei表示三个方向上的拉压弹性模量；

μij表示六个泊松比，第一个指标i为作用力方向，第二个指标j代表变形方向；

Gij表示三个对称面上的剪切模量。

Ei的测试可以通过拉伸或压缩的方法测定。剪切模量Gij似乎较难以测定。测定剪切弹性模量的方法有很多，如：45°偏轴拉伸试验法、轨道剪切法、圆轴长杆扭转试验法等。本文尝试用三点弯曲试验方法即分离刚度法来测定Glt、Glz。

2 分离刚度法的测试原理及理论证明

2.1 分离刚度法的测试原理

分离刚度法的测试原理如图1所示。它为一根双外伸简支梁，中间受一集中力，在梁的中点及两端外伸点分别用千分表测定其挠度。根据一阶剪切变形理论，图中梁中点C的挠度为：

式中：D＝EI（E为梁纵向弹性模量，为梁横截面对中性轴的惯性矩）；

C＝GA（G为梁横截面方向的剪切弹性模量，A为梁的横截面面积）。

上式表明，C点挠度有两部分组成，一部分与弯曲刚度D有关，由弯矩引起的，即所谓纯弯挠度，用WM来表示；另一部分与剪切刚度C有关，由横向剪力引起，即所谓横向剪切挠度，用WQ表示之。k为横截面剪切修正系数，若为矩形横截面，则k＝3／2。

这样，（2）式可写为：

实际测量得到的C点挠度是含有弯矩与剪力共同作用下的总挠度。如何将它们分离，是解决问题的关键所在。

（3）式是在直法线假设条件下得到的。因此，变形后的横截面仍为平截面。不过此时的横截面不再与弯曲后的梁轴线垂直，发生了一定偏转。但是，由剪力产生的截面转角相对弯矩产生的要小得多。因此，可以认为，支座处的截面转角仅有弯矩产生。又由于外伸段横截面上无内力，所以，外伸段只随同支座处横截面发生了刚性转动。此时只要知道支座截面处的转角，利用三角关系，容易求得外伸自由端A或B产生的位移即挠度。另外，由复合材料结构力学经典理论容易得到，当梁外伸端时，外伸端A或B处挠度即为梁中点挠度的纯弯部分。即

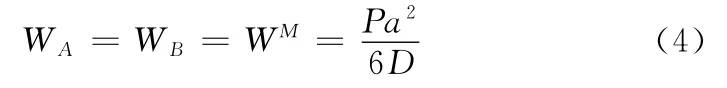
将（4）式代入（3）式可得到：

观察（5）式，容易看出，只要通过测定梁中点C及自由端A或B的挠度值，利用（5）式就可确定出剪切刚度；显然，利用（4）式，就可确定出弯曲刚度D。这样，在同一试验中，可同时测定弯曲刚度D与剪切刚度C，实现了这两个刚度的分离。弯曲刚度D只与外伸端挠度有关，但剪切刚度C决定于跨中点和外伸自由端两点挠度之差，而且实现分离出剪切刚度仅当外伸段长度b＝2a／3时才行。

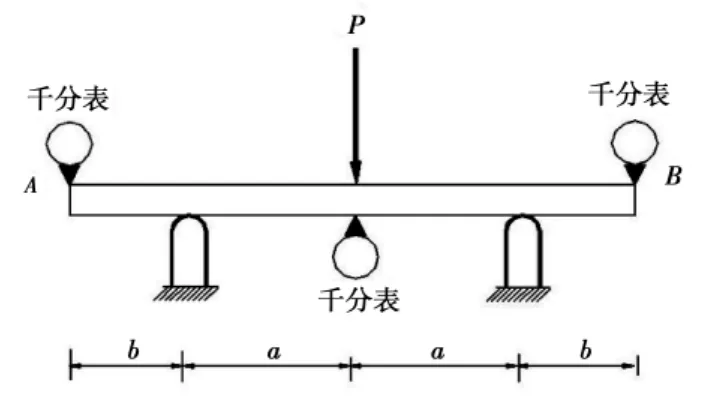
图1 分离刚度法测试原理

2.2 分离刚度法的测试原理

用功的互等定理来证明分离刚度法。设图2所示为用复合材料制作的梁分别处于两种不同的受力状态，并认为梁在载荷作用下处于小变形、线弹性阶段。

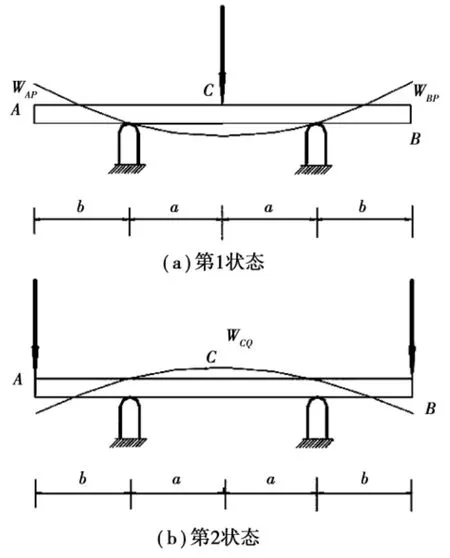
图2 复合材料梁不同的受力状态

这样第1状态外力在第2状态位移上所作的功等于第2状态外力在第1状态位移上所作的功。即：

式中，WCQ为Q力作用下引起的C处挠度，WAP、WBP为力P作用下引起的A、B两处的挠度。

由于对称性，引起的两外伸端A、B处的挠度相等，即WAP＝WBP，显然，它们的数值与外伸段长度b有关，是b的函数，所以可表示为WAP＝WBP＝W（b），这样，（6）式可写为：

（8）式表明，第2状态下梁中点的挠度WCQ可通过第1状态下梁外伸端A或B处的挠度来表示。由于第2状态梁跨中间段处于纯弯状态，因此梁跨内各点处的曲率相等，根据经典理论，可表为：

式中，M（b）为梁跨中间段横截面上弯矩，ρ为梁跨中间段挠曲线曲率半径。

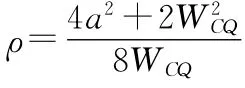
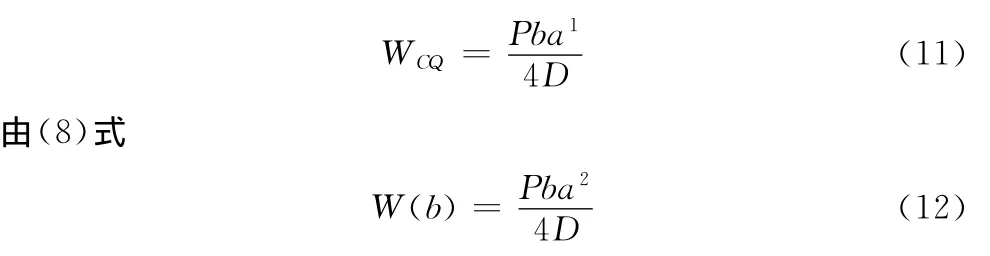
由于W（b）为第1状态下的外伸自由端处挠度，可通过试验测定，这样，弯曲刚度可通过（12）式算得。令式（12）中的b＝2a／3，则外伸自由端A或B处挠度为：

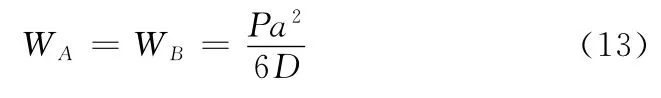
上式即为图2所示跨中点挠度的纯弯部分。

因此，要确定与梁弯曲刚度有关的弯曲挠度，只需测定外伸端挠度，不过此时须有b＝2a／3。否则，外伸端挠度不等于跨中挠度的纯弯部分。通过（13）式将C点处由弯矩产生的挠度分离了出来。

至于与剪切刚度有关的剪切挠度，我们注意到，已经测得了图1所示的梁中点挠度与外伸自由端挠度，这样，利用（5）式就可算出剪切挠度部分，即

所以可通过下式计算剪切模量：

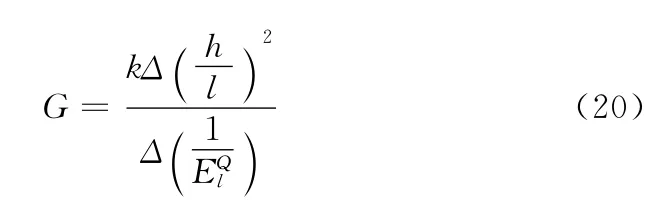
至此，既从理论上严格地证明了图1所示的试验方法的可行性与正确性，同时又推导了剪切模量的计算公式。

3 试验过程

3.1 试验材料与设备

试验材料：本文中用材料为同一批次意杨（拉丁名）单板层积材，来源于浙江诸暨某木材厂，用酚醛树脂胶以冷压法制得。方材尺寸为：2000mm×300mm×150mm，共3根，平衡含水率为10%左右。在南京林业大学木工机械实验室按照一定的规格尺寸进行试件加工。分别从三根方材上制取试件（610mm×40mm×25mm）5块；试件（610mm×40 mm×25mm）7块。试件制备完毕，用酒精清除表面灰尘、杂质等异物。

试验设备：SANS万能力学试验机（20kN）；游标卡尺，精度为0.02mm；电阻应变片，灵敏度为0.9217，DH3818静态应变测试仪，WYS－1材料力学试验台，浙江大学材料力学实验室，大力机电科技公司联合研制；BLR 型拉压力传感器；测力器SCLY－2数字测力仪；百分表、千分表等。

图3 试件制取

3.2 试验方法

采用三点弯曲分离刚度，测得中点挠度及外伸梁挠度。测试不同跨高比（7.2、9.6、12.）情况下含剪弹性模量并计算剪切模量。

4 结果与分析

4.1 数据处理

测得LVL含剪弹性模量见表1，计算得剪切模量见表2。

表1 LVL梁在不同跨高比下含剪弹性模量测试值

表2 LVL梁不同平面剪切模量计算值

4.2 数据分析

由表1、表2看出，在同样增量载荷下，垂直加载（加载方向与胶层垂直）测得的含剪弹性模量大于平行加载（加载方向和胶层平行）测得的含剪弹性模量，L－T、L－Z平面的剪切模量不一样，这说明对单板层积材各向异性的特征。同时也可以看出随着跨高比增大，含剪弹性模量增加量有减小的趋势，这与理论分析是相符合的。说明跨距增大，剪切效应逐步减弱，含剪弹性模量越接近于纯弯曲弹性模量。从变异系数来看，测试值的变异系数在正常范围之内，数据是可信的。含剪弹性模量与剪切模量的比值在范围之内［9］，说明数据是基本准确的。

从表2可以看出，L－Z平面的剪切模量大于L－T平面的剪切模量，说明b试件抗剪变形能力较强。

5 结论

1）LVL可以认为和木材一样，是正交各向异性材料；

2）用分离刚度法测试LVL的面内剪切模量简便，能表征LVL真实的材料性能，具有实际的应用价值。

［1］Llaufenberg T.Exposure effects upon performance of Laminatedveneer lumber and glulam materials［J］.Forest Product Journal，1982，32（5）：42－8.

［2］Semra C，Gursel C，Ismail A.Effects of logs steaming，veneer drying and aging on the mechanical properties of laminated veneer lumber［J］.Building and Environment，2007，42：93－98.

［3］Wang X，Ross R J，Brashaw BK，et al.Flexual Properties of laminated veneer lumber manufactured from ultrasonically rated maole veneer.Forest Product Laboratory，FPL－RN－0288，2003.

［4］Hing P S，Paridah M T，Zakiah A.Edgewaise bending properties of LVL：effects of veneer thickness and species［C］／／.the Proceeding of USM－JIRCAS joint international symposium，lignocelluloses－material of the millennium.2005：3－14.

［5］卫佩行，周定国.人造板机电包装材料应用现状及前景［J］.林业科技开发，2012，26（1）：13－16.

［6］阮锡根，余观夏.木材物理学［M］.北京：中国林业出版社，2005.

［7］王丽宇，鹿振友，申世杰.白桦材12个弹性常数的研究［J］.北京林业大学学报，2003，25（6）：64－67.

［8］邵卓平，祝山.电阻应变法测定杉木弹性常数的研究［J］.安徽农业大学学报，2001，28（1）：32－35.

［9］F.F.P.科尔曼等著，杨秉国译，木材学与人造板工艺学原理（人造板）［M］.北京：中国林业出版社，1984.