填土含水率对挡土墙土压力影响的实验分析

赵吉坤，温娇娇

（南京农业大学 工学院，南京 210031）

挡土墙是支挡墙后土体使其不发生坍塌的结构。根据工程的实际需要，挡土墙可用于支挡河岸边坡、船闸、桥台等建筑物，也可用于地下室，山区建筑需要错层时支挡土体或深基础开挖护壁等［1］。在一般的工程中，重力式挡土墙的应用最为广泛。重力式挡土墙存在着多种失效模式，如挡墙水平滑移、整体滑移、挡墙倾覆、墙底地基土承载力不足、管涌和流砂等［2］。土压力是影响挡土墙稳定性的一个很重要的因素，而影响土压力的很重要的一个因素就是填土的物理力学性质，包括土的重度、含水量、内摩擦角和粘聚力。同一土质的颗粒级配和含水率不同，就会导致土压力的不同，进而影响挡土墙的稳定性。为了保证挡土墙可以充分发挥防护作用，必须对挡土墙后填土的物理、力学性质进行研究与分析，这样既有利于挡土墙类型的选择，也有助于挡土墙尺寸的设计。土的抗剪强度是土强度特征的重要指标之一，直接影响建筑物的结构与稳定。填土的含水率的变化直接影响土体抗剪强度指标的改变，进而影响挡土墙所受土压力大小。目前国内外研究人士已对含水量与抗剪强度指标的关系进行了许多研究。

三轴剪切由于其仪器的特性，得出的结果更为客观，更接近自然情况。目前已有不同的研究人员提出了许多预测非饱和土抗剪强度的公式，例如Khalili和Khabbaz等［3］利用14种土的实验结果给出了14种土的有效应力参数和基质吸力的关系，通过实验数据分析得出有效应力参数与基质吸力的拟合曲线，进而得出非饱和土抗剪强度公式。边加敏等［4］采用控制变量法采用不固结不排水条件下的直剪实验来研究抗剪强度指标各参数与含水量的关系，实验得出粘聚力C、内摩擦角φ与含水率之间的关系分别用二次曲线与直线的关系进行拟合是满足要求的。相关系数达到了0.91以上。研究含水率对抗剪强度的影响，最终还是分析其对土压力的影响。杨磊［5］以黄土为研究对象进行直接剪切实验，结果表明含水率和干密度是影响黄土抗剪强度的重要因素，在快剪试验条件下，原状土应力与位移关系曲线有一转折点，曲线转折点前陡后缓，重塑黄土应力随着位移的逐渐增大而增大，曲线无峰值点。Yong和Daehyeon［6］基于圆锥贯入试验（CPT）对粘性土进行剪切试验，提出了提高粘土不排水抗剪强度相关性的合理方法。并且对印第安纳州的九个地点粘性土抗剪强度进行调查，结果发现锥因素随着土的塑性指数增加而增加。

目前对土压力的研究主要涉及到挡土墙土压力的计算、挡土墙的稳定性能等等。王元战等［7－8］假设水平土层间剪应力与竖向土压力强度比值为某一常数，对挡土墙绕墙脚和强顶转动时的土压力强度进行计算。王平，刘东燕等［9］对挡土墙滑移破坏与倾覆破坏的可靠性进分析，发现在安全系数相同时滑移破坏的失效概率高于倾覆破坏的失效概率，并且在进行重力式挡土墙抗震设计时，应使两种失效概率接近，以达到安全经济的目的。肖衡林，余天庆［10］通过对山区挡土墙土压力进行现场试验研究，发现刚施工完成的挡土墙土压力为非线性分布，近似成双直线，实际土压力合力介于静止土压力合力和垂直土压力合力之间，且土压力随时间变化总趋势是不断增加。张永兴，陈林［11］改进库伦极限平衡理论，用于非极限状态主动土压力的研究，采用水平微分单元法求解刚性挡土墙平移模式下非极限状态主动土压力，得到挡土墙土压力和合力作用点的理论公式。魏焕卫等［12］以不同土压力状态与静止土压力状态时的土压力差值计算分布力，基于Mindlin应变解建立了任意土压力变化下的土体侧向位移计算模型，利用该计算模型可以得到不同位移限值要求下的侧向土压力，从而为不同工程中土压力的合理取值提供了理论依据。LIU［13］采用有限元法对加筋挡土墙加固的影响蠕变的参数进行了分析，并将实验结果与美国联邦公路局采用内部稳定性分析方法所得的结论进行比较，发现采用有限元法计算出的结果与工程实例贴合较好。如何提高建筑物结构的抗震性一直是近年来各国研究的重点，也不乏对于挡土墙的抗震性研究。LIN等［14］研究了挡土墙在特定地震荷载影响下的动态响应规律，结果表明，随着内摩擦角、基础斜度、填土的凝聚力和最大的动态弹性模量的增加，挡土墙的最大应力减小；而当地震频率和地震输入峰值跌落时，挡土墙的最大应力增大。Guler和Selek［15］利用在Kandilli天文台的振动台设备和土耳其博阿齐大学的地震研究所对土工织物加筋土挡土墙模型进行了测试，更好地了解了加筋土挡土墙的动态行为。初步试验结果表明，在森特罗地震记录中幸存的土工织物加筋土城墙几乎没有永久性位移。

目前挡土墙的应用已经非常广泛，技术也相当成熟。前人从微观机理及宏观物理实验角度研究分析了挡土墙的性能并对挡土墙墙后填土的力学性能进行了试验研究。本实验将研究目标锁定在填土的含水率，进行实验得出含水率对填土抗剪强度的影响参数，数值模拟实验分析得出比较具可用性非饱和填土的含水率 粘聚力、含水率 内摩擦角之间的关系式。并对不同含水率状态下的填土进行挡土墙加压试验，根据朗肯理论求出挡土墙所受到的土压力，实验分析得出含水率 主动土压力、含水率 被动土压力之间的关系式。

1 含水率影响土压力强度的理论模型

边加敏等［6］采用不固结不排水条件下的直剪试验来研究抗剪强度指标各参数与含水量的关系，实验得出了如下关系式：

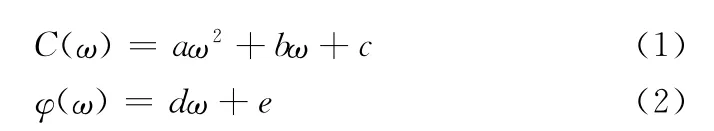
其中a、b、c、d、e均为待定的参数。本文以以上两个公式为基础进行实验，通过实验确定以上未知的待定参数，并根据实验结果对公式（1）、（2）进行修正。

当挡土墙模型为墙背垂直，填土表面水平时，其土压力计算适用于朗肯理论，土压力计算简化模型如图1所示，根据图1计算简图及公式（2）得到土压力系数和含水率之间的关系式如公式（3）、（4）所示：

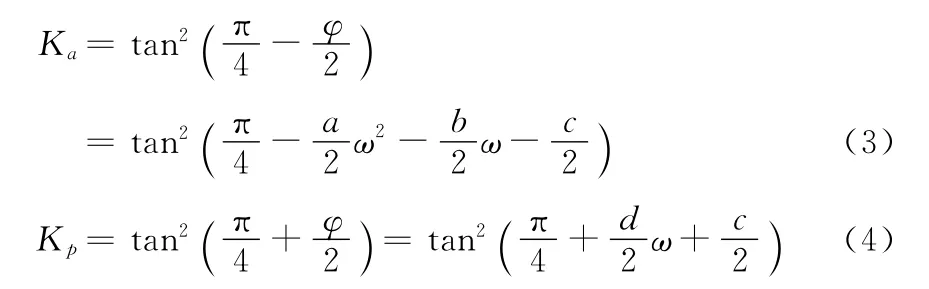
图1 土压力计算简图

由公式（1）、（3）、（4）及图1的土压力计算简图，根据郎肯土压力理论，可以得到主动土压力与含水率之间的关系式为：

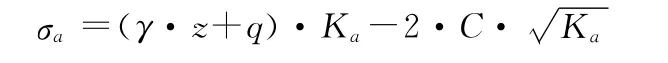
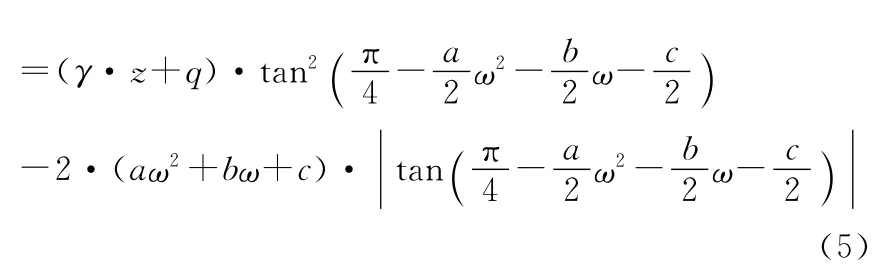
被动土压力与含水率之间的关系式为：

其中γ为土样重度，取20kN／m3，q＝q0＋qi，0≤z≤H

以上内容为在前人研究的基础之上对实验整体的理论模型构建部分，以下内容以南京农业大学校内土样为例，进行一系列实验确定以上待定参数a、b、c、d、e，并在有必要的情况下，根据实验数据对公式进行修正，然后进行实验验证公式（5）、（6）的适用性。最后，根据实验直接数据转换过来的土压力结果，拟合出填土含水率与挡土墙所受土压力之间的关系式。

2 实验设计

2.1 原材料简介

水泥为原产于南京海螺水泥有限公司海螺牌32.5R普通硅酸盐水泥，表观密度为3100kg／m3。砂为普通河砂，细度模数为2.77。土样为学院内地表取土。水为学院内实验室自来水。天然骨料为级配连续的碎石，最大粒径为25mm。

2.2 实验用挡土墙试块设计与制作

本实验所用挡土墙为普通重力式混凝土挡土墙，尺寸为300mm×250mm×40mm，其中墙趾宽为40mm，如图2（a）所示。

图2 试块设计

根据《普通混凝土配合比设计规程》按照普通混凝土的配合比设计方法确定本实验砼的配合比为——水泥∶砂∶石子∶水＝1∶1.157∶2.465∶0.41，砼的拌制过程严格按照《建筑材料》相关规范进行，并且在浇筑前对砼的工作性进行了测定，得到工作性良好的混凝土。模具限制采用人工振捣密实后磨平表面，实验室室内环境自然养护14d。浇筑成型的挡土墙试块如图2（b）。

2.3 实验仪器与模具

施加竖向压力的主要设备为一台WAW－600B型微机控制电液伺服液压万能试验机，最大实验力为600kN；测量含水率的设备为一台北京产电子控温远红干燥箱；测量颗粒级配的设备为一套新标准砂石筛。实验模具主要有制作挡土墙时的支护模具和加压实验所用的维护模具。支护模具所用材料为木板；维护模具所用材料为10mm厚钢板。实验设备与实验模具见图3。

图3 实验装置与模具

3 实验及结果分析

3.1 颗粒级配分析

由于实验室仪器设备的制约，本实验中土的颗粒级配实验采用砂石颗粒级配的做法来做，所用设备为“新标准砂石筛”。本实验前期设想为采用两种颗粒级配的土样进行对比实验，其中级配1位原土样级配，级配2为原土样级配按照比例添加碎石和砂配制而成，两种土样的颗粒级配曲线如图4所示。据砂石颗粒级配计算方法得出级配1要优于级配2，所以以下实验研究基于级配1完成。

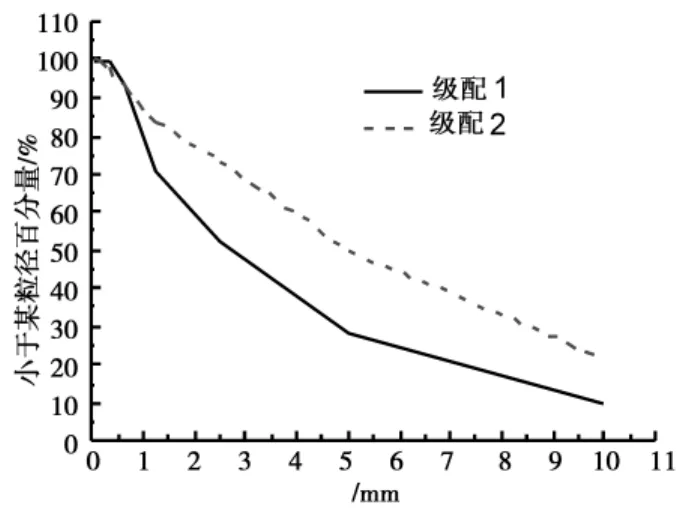
图4 颗粒级配曲线

3.2 含水率影响抗剪强度指标相关参数的确定实验分析

本实验为了确定上述关系式中的参数，利用ZJ型应变控制直剪仪，在不同的垂直压力下进行不固结不排水剪切，求得破坏时的剪应力，最后利用软件拟合剪应力与垂直压力的相互关系，确定各含水率对应的抗剪强度指标C和φ，直剪试验剪应力与垂直压力数值拟合结果如图5所示。

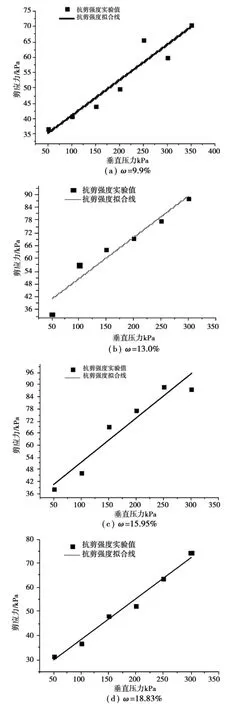
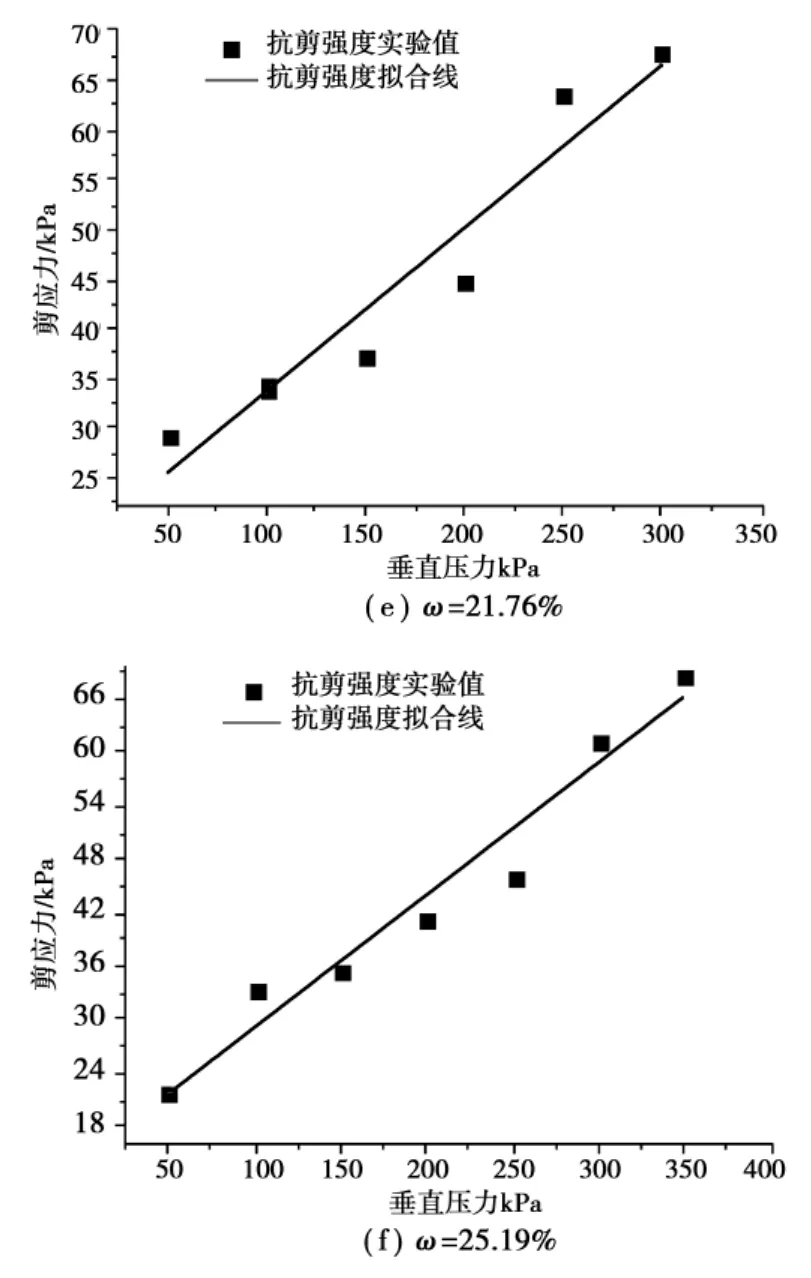
图5 直剪试验数值拟合

通过图5可以发现，同一含水率条件下，剪应力值均匀的分布在拟合线两侧，即剪应力与垂直压力表现出较好的线性相关性。上述曲线中也存在个别点偏离拟合线程度较大，这主要是因为试件制备的不规范以及实验过程中的操作误差造成，极度影响拟合性的数据（及瑕疵点）已被剔除。观察6组图形可以发现，以上的数值模拟数学模型符合公式y＝mx＋n，其中m为斜率，数值上等于内摩擦角的正切值，即m＝tanφ；n为截距，数值上等于粘聚力，即m＝c。则有关系式如下：

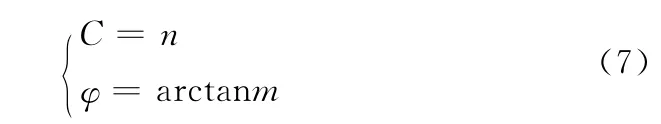
据图5及公式7，计算得出土样抗剪强度指标实验数据如表1所示。

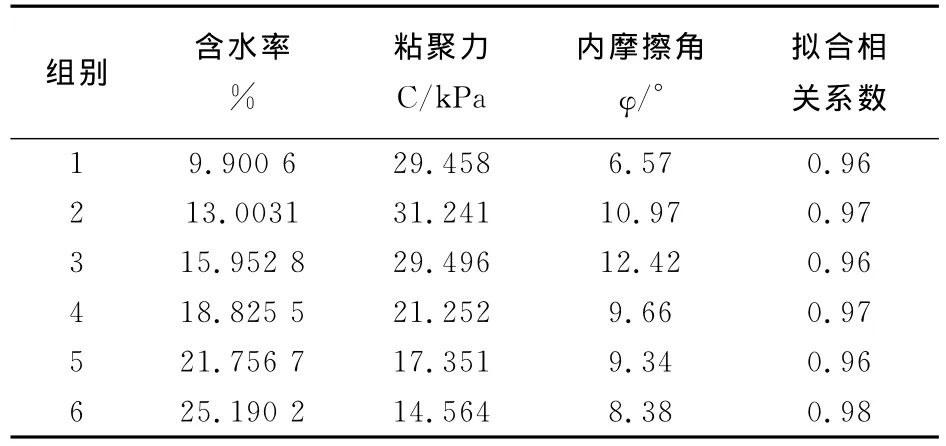
表1 土样抗剪强度参数实验数据

根据表1的实验数据，拟合出本文土样含水率 粘聚力、含水率 内摩擦角之间的关系式。粘聚力C与含水率之间的关系式为：

数据显示拟合优度为93.5%，拟合性较好。比较公式（1）、（2）与（8）、（9）可以发现，公式（8）与公式（1）对应的较好，并且以较高的拟合度给出了相关待定系数的数值，即a为－0.0226，b为－0.31035，c为35.91649；但是公式（9）与（2）即内摩擦角与含水率的关系式不相符，本文实验研究显示内摩擦角与含水率呈现二次曲线关系，且拟合性较好，故此得到公式（2）的修正公式为：

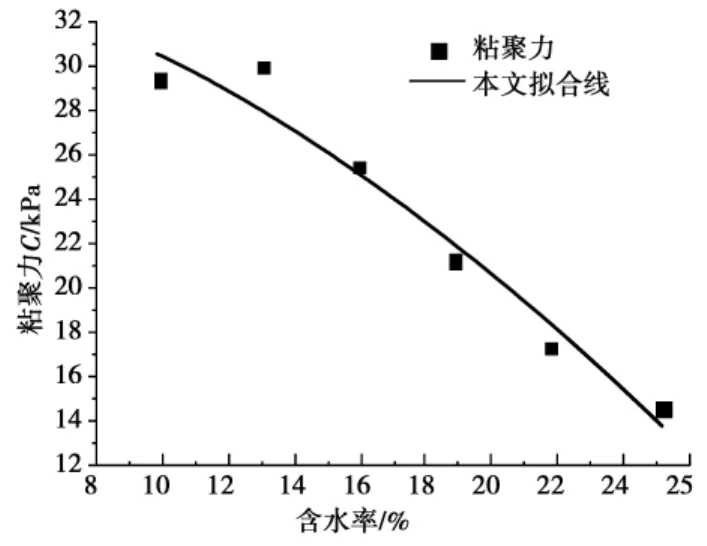
图6 粘聚力与含水率拟合曲线

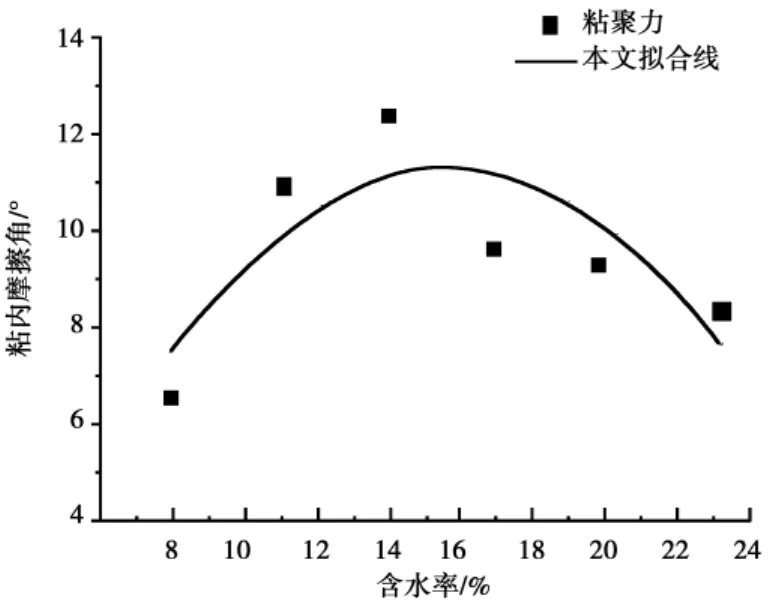
图7 内摩擦角与含水率拟合曲线

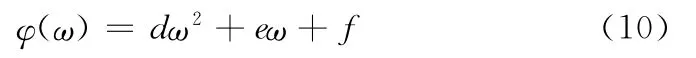
其中参数d为－0.06295，e为2.22048，f 为－8.34995。出现以上理论与实际试验的差异也是实验之前料想到的，首先，因为实验土样与理论研究中所用的土样并不一致，所以在实验研究时结果必定会存在偏差；其次，实验试件制作的不规范性及实验方法与实验操作都会令实验结果出现偏差。根据修正过的公式（10）对公式（4）、（6）进行修正得到公式如下：

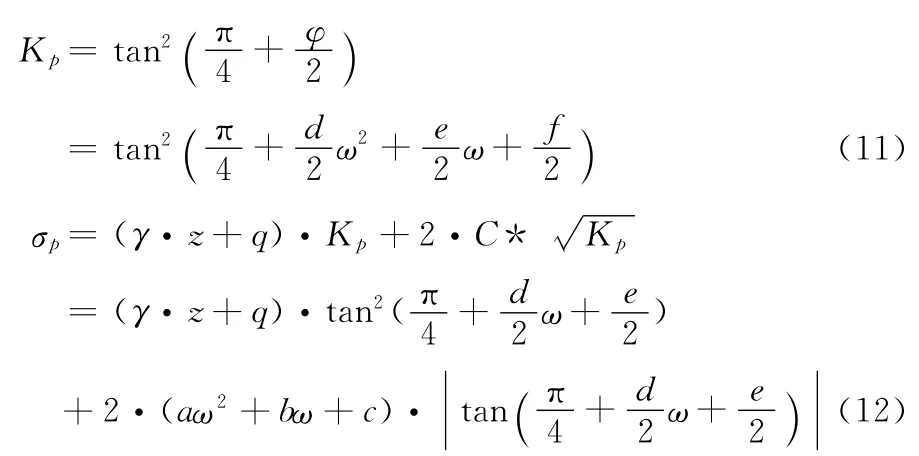
由以上实验得知，待定参数的相关数值为a为－0.0226，b为－0.31035，c为35.91649，d为－0.06295，e为2.22048，f为－8.34995。

3.3 填土含水率分析

采用不同含水率的填土，进行挡土墙加压试验。为了能够让土样湿度充分均匀，每组土样含水率配置好之后，采用保鲜膜封闭，实验室室内环境静止24小时。含水率的测定采用烘箱法，每组土样含水率取3个试样，在烘箱105℃条件下烘干390min，含水率计算公式为：

其中m0为土样铝盒质量，m1为铝盒加湿土的质量，m2为铝盒加干土质量。根据公式（13）计算出填土含水率情况如表2所示。

表2 含水率数据

3.3 加压试验介绍及分析

实验现象：加压初始时，挡土墙表现为墙顶首先向外倾斜，当倾斜到一定程度时开始出现墙趾外移，因为模型尺寸限制，当挡土墙已经破坏之后仍可以继续加压，而实质是在纯压土，将土样压实，故此在实验时判断实验结束标准为挡土墙墙趾完全移出。

加压实验采用的方法为施加应变，试验仪器为万能试验机，利用混凝土块作为传力媒介，并借用钢板将集中力转化为均布力，其整体试验模型如图9，实验中保持填土颗粒级配一致（级配1），填土密实度基本一致（孔隙比见表3），以此来确保土压力的差异是由填土含水率不一致引起的。

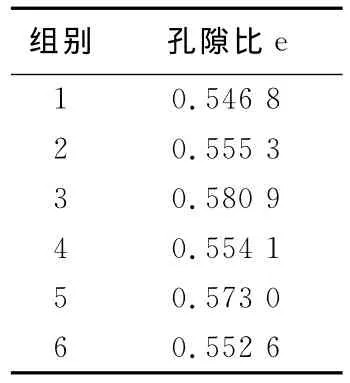
表3 孔隙比实验数据

图9 加压模型

据公式（5）、（12）以及表2含水率数据，计算出挡土墙主动土压力、被动土压力如表4所示，其中σa0表示墙顶主动土压力强度；σa1表示墙址主动土压力强度。σp0表示墙顶被动土压力强度；σp1表示墙址被动土压力强度。qi为跟据加压试验测得极限荷载与恒载之和除以受力面积所得。

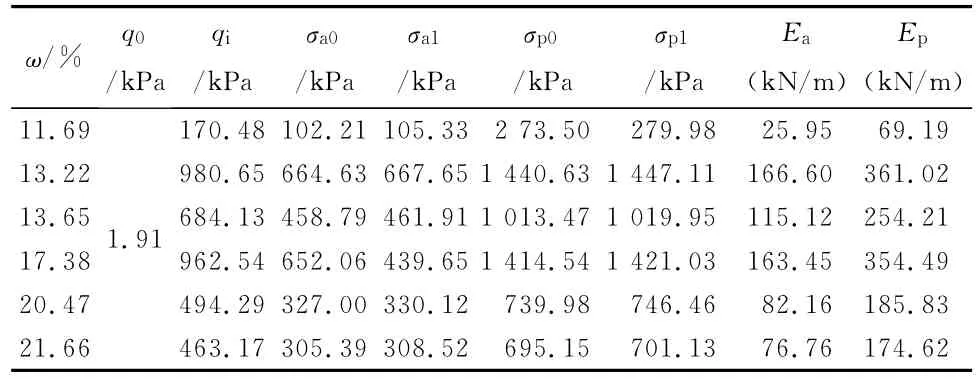
表4 土压力计算

对计算得出的土压力进行分析整理，得出土压力与含水率的关系式，土压力与含水率的拟合曲线如图10、11所示。

据拟合曲线得到主动土压力 含水率关系（公式11）和被动土压力 含水率关系（公式12）如下所示：

图10 主动土压力与含水率拟合曲线

图11 被动土压力与含水率拟合曲线

为了验证公式（14）、（15）的正确性，对其他不同含水率的相同土样在相同的实验条件下进行实验，将实验直接测得的极限力转换为挡土墙受到的土压力，并与拟合公式计算结果进行比较。表5给出了不同含水率条件下的主动土压力、被动土压力实验计算值与拟合公式（14）与（15）的相对差值，相对误差计算方法为公式计算结果与实验转换结果之差的绝对值与实验转换结果的比值，以百分数表示。

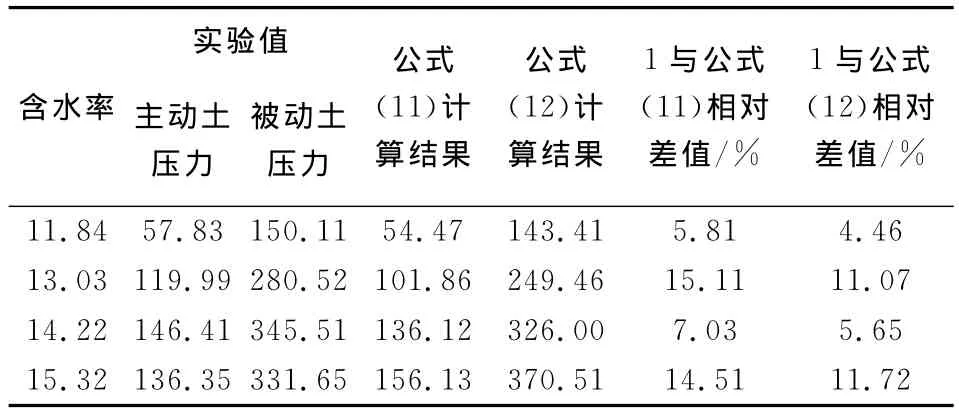
表5 公式与试验结果的相对差值

由表5可以看出，拟合公式（14）与实验值的相对差值在5.81%－14.51%之间，拟合公式（15）与实验值的相对差值在4.46%－11.72%之间，拟合结果较好。从这里我们也可以看出填土含水率对挡土墙稳定性能的影响，随着含水率的增大，重力式挡土墙所能承受的最大土压力有所增大；当含水率超过某一界限值时，最大土压力随着含水率增大而减小。这也说明，存在着某一界限含水率（即最优含水率），使得重力式挡土墙所能承受的最大土压力最大，也即挡土墙更趋于稳定性的可能性更大。

4 结 论

1）在前人对含水率影响土样抗剪强度指标研究的基础上，本文针对当地土样进行实验，通过对实验数据的数值拟合分析，确定了含水率对抗剪强度指标的影响系数，得到粘聚力 含水率关系式、内摩擦角 含水率之间的修正关系式。最后，本文又根据加压试验土压力数据，推导出土压力强度与含水率之间的本构方程。

2）根据理论推导出的土压力强度 含水率关系式，进行挡土墙加压试验，观察不同含水率条件下挡土墙受力破坏情况及土压力情况。加压过程中发现，随着试验力的增大，挡土墙首先发生墙顶向外倾斜，当倾斜发生到一定程度后墙身整体向外移动直至破坏；由于含水率的影响，填土承受的荷载与其压缩性之间呈现非线性关系。

3）根据土压力－含水率关系式（公式11、12）可以看出，土压力与含水率之间存在着二次曲线关系，由图10、11可知，本实验中当含水率为介于16%－18%中间的某一值是，能够使得挡土墙所能承受的最大主动与最大被动土压力均为最大，也即此时挡土墙趋于稳定性的可能性更大。

［1］朱凡，胡岱文.土力学［M］.重庆：重庆大学出版社，2004.

［2］赵国藩.工程结构可靠度理论与应用［M］.大连：大连理工大学出版社，1996.

［3］Khalili，Khabbaz M H.A unique relationship for the determination of the shear strength of unsaturated soils［J］.Geotechnique，1998，48（5）：681－687.

［4］杨磊.黄土抗剪强度特定分析［J］.水利与建筑工程学报，2010，8（3）：163－165.

［5］边加敏，王保田.含水量对非饱和土抗剪强度参数的影响研究［J］.地下空间与工程学报，2011，7（1）：17－21.

［6］Yong S，Daehyeon K.Assessment of undrained shear strength based on Cone Penetration Test（CPT）for clayey soils［J］.KSCE Journal of Civil Engineering，2011，15（7）：1161－1166.

［7］王元战，李蔚，黄长虹.墙体绕基础转动情况下挡土墙主动土压力分布［J］.岩土工程学报，2003，25（2）：208－211.

［8］王元战，唐照评，郑斌.墙体绕墙顶转动情况下挡土墙主动土压力分布［J］.应用数学和力学，2004，25（7）：695－700.

［9］王平，刘东燕，黄海斌，雷用.挡土墙安全系数的抗震可靠性分析［J］.四川建筑科学研究，2010，36（2）：195－197.

［10］肖衡林，余天庆.山区挡土墙土压力的现场试验研究［J］.岩土力学，2009，30（12）：3771－3775.

［11］张永兴，陈林.挡土墙非极限状态主动土压力分布［J］.土木工程学报，2011，44（4）：112－119.

［12］魏焕卫，杨敏，贾强，等.基于Mindlin解的土压力位移计算模型［J］.岩土力学，2011，32（2）：495－502.

［13］Loin H B.Internal Stability Analysis of Segmental Geogrid－Reinforced Soil Retaining Walls［J］.Geosynthetics in Civil and Environmental Engineering.2009，4：322－327.

［14］Lin Y L，Liu Y，Li J.Dynamic response law about gravity retaining wall to seismic characteristics and earth fill properties［J］.Journal of Central South University of Technology，2012，19（3）：657－663.

［15］Guler E，Selek O.Reduced Scale Shaking Table Tests on Geosynthetic Reinforced Soil Retaining Walls［J］.Geosynthetics in Civil and Environmental Engineering，2009，4：295－299.