微细颗粒物在过滤介质中过滤特性的CFD－DEM模拟

于先坤，钱付平，鲁进利

（安徽工业大学 建筑工程学院，安徽 马鞍山 243002）

近年来，工业的迅猛发展伴随着严重的环境污染问题，空气中含有大量的有害气体（SO2、NOx）和细小的悬浮颗粒物，对人类的呼吸免疫功能、呼吸道和中枢神经系统造成严重危害，因此环保任务刻不容缓。“十二五”规划纲要也明确提出，到2015年达到主要污染物排放总量显著减少的目标，其中颗粒物特别是微细颗粒物（PM2.5）仍将是城市大气污染物防治的重点。纤维过滤作为一种先进的过滤技术已得到越来越广泛的应用，国内外已有众多学者对不同排列结构的纤维过滤介质气 固两相流动进行了数值模拟研究［1－5］，这些模拟大都基于Fluent软件，利用Eulerian－Lagrangian方法中的颗粒轨道模型（Lagrangian Particle Tracking，LPT）［6］计算微细颗粒在过滤介质中的运动特性，而且，这些数值研究仅仅针对过滤介质的洁净过滤阶段（或称稳态过滤阶段），对于过滤介质的含尘过滤（或称非稳态）阶段，除了考虑气 固之间的曳力、布朗力外，还需考虑颗粒与颗粒及颗粒和纤维之间的作用力。离散单元法（Discrete Element Method，DEM）是分析与求解复杂的离散系统运动问题和力学问题的一种新型数值方法，可以描述颗粒间的碰撞、团聚等特征。在处理气 固两相中固相方面具有其它方法无法比拟的优越性。DEM方法最初应用在气 固流动时主要针对较大尺寸的颗粒，近年来，随着计算机技术的发展，已有研究者利用DEM方法处理微米级颗粒［7－9］。另外，结合计算流体力学（CFD）在处理气相流场方面的优势，可以将DEM与CFD结合起来，发挥各自的优势，弥补不足，并且可以提高数值求解的计算效率和精度，扩展应用范围。Tsuji［10］最早将DEM与CFD相结合来解决二维的气 固流化床问题，开创了DEMCFD耦合的先例。国内方面，文献［11－13］利用 CFD－DEM方法对下行床内气固流动及混合行为、三维风沙运动及弯管中柱状颗粒的输送行为等进行了数值研究。这些研究大大丰富和拓宽了CFD－DEM方法的应用范围，然而，目前国内外较少有利用该方法模拟微细颗粒在过滤介质中运动行为的。

本文利用CFD－DEM方法计算微细颗粒在随机排列过滤介质中的过滤特性，计算时充分考虑颗粒群组成、粒径分布、纤维直径分布、颗粒间及颗粒与纤维间的反弹作用以及颗粒团聚等因素。根据计算结果，分析纤维过滤中颗粒、纤维尺寸及过滤参数等对过滤介质过滤性能的影响。所得结果对发展纤维过滤理论技术及优化过滤介质结构及过滤参数具有重要的理论和现实意义。

1 CFD－DEM数学模型

考虑到在实际过滤过程中颗粒所受到的力十分复杂，为方便模拟，忽略了电场力和分子间范德华力对颗粒运动行为的影响；只考虑气流曳力、颗粒间碰撞力、颗粒与纤维反弹力、颗粒重力以及布朗力对颗粒的作用。过滤过程中颗粒i平移和旋转所受到的作用力可表示为［8］

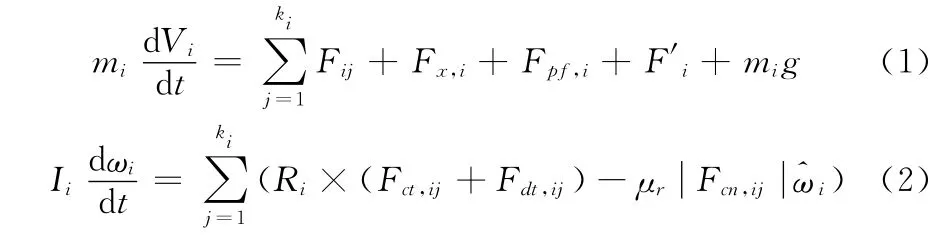
式中，mi，Ii，Vi，ωi分别为颗粒i的质量、惯性矩、平移及旋转速度；Ri为从颗粒i中心到接触点的矢量；ki为和颗粒i接触的颗粒数；μr为滚动摩擦系数＝ωi／｜ωi｜；所涉及到的力包括颗粒自身的重力mig、颗粒之间的碰撞力Fij（法向接触力Fcn，ij、切向接触力 Fct，ij、法向粘性阻尼力 Fdn，ij、切向粘性阻尼力Fdt，ij）、布朗力Fx，j、颗粒与纤维碰撞时的反弹力 Fi以及′颗粒与流体之间的作用力Fpf，i。

颗粒间的碰撞力Fij是作用在颗粒i上的弹性力（法向力）和阻尼力的合力，根据Hertz接触理论，可表示为

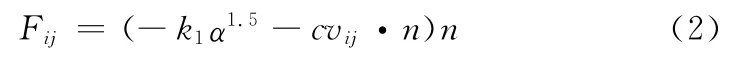
其中，α是法向重叠量，vij是颗粒i相对于颗粒j的速度，n是颗粒i球心到颗粒j球心的单位矢量，k1是颗粒i与颗粒j的法向弹性系数，c是颗粒i的法向阻尼系数。

同理，颗粒与纤维介质碰撞时，作用在颗粒i上的反弹力Fi′可表示为

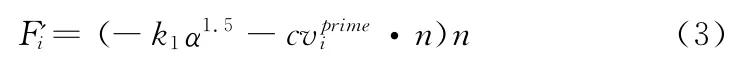
其中，vi′为颗粒i相对于纤维介质的速度，k2是颗粒i与纤维法向弹性系数。

结合文献［8］和［14］中相关系数的介绍和设置，本文中的颗粒与颗粒、颗粒与纤维的反弹（恢复）系数，摩擦系数，黏附能量密度，材料属性以及其他相关的模拟参数如表1和2所示。

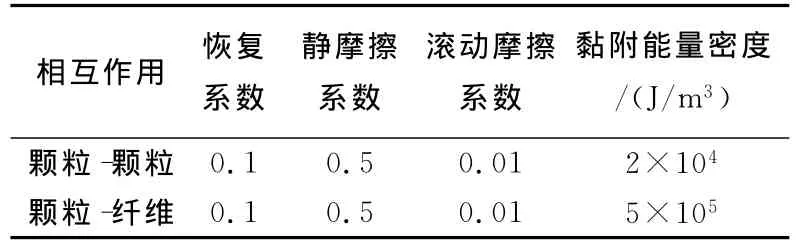
表1 接触属性参数

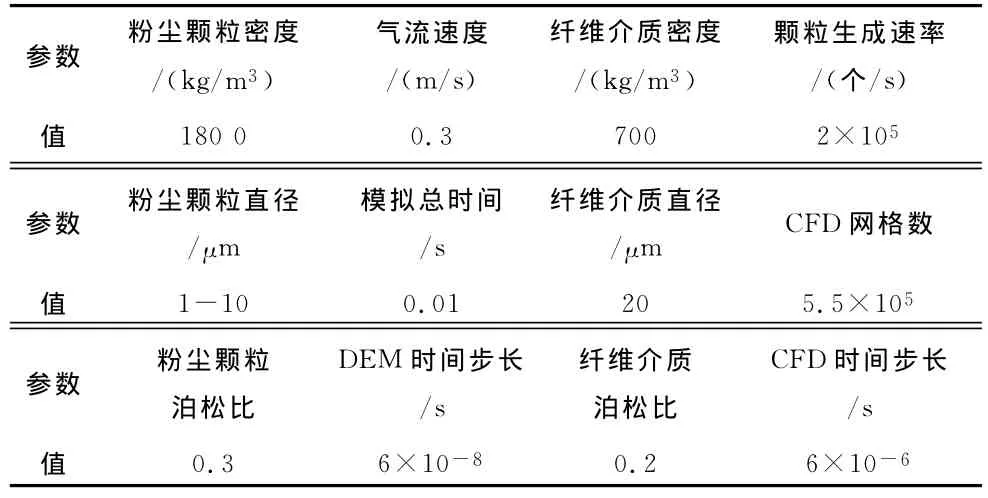
表2 模拟参数

对于通过过滤介质的气体，基于计算单元内局部平均变量的质量及动量守恒（N－S）方程可以由下式表达［8］：

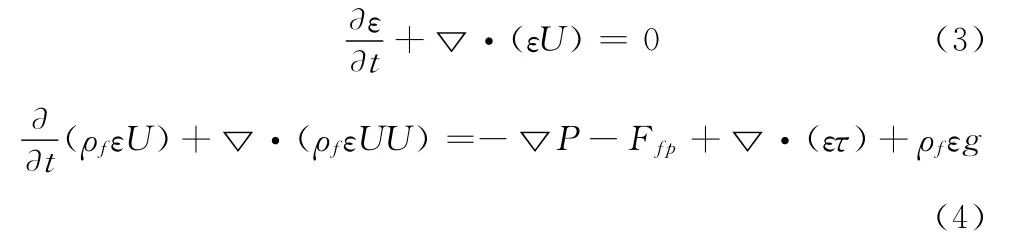
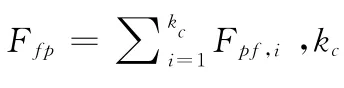
图1给出了CFD－DEM耦合计算的基本流程，即首先通过CFD技术求解气相流场，将流场信息通过曳力模型转化为DEM中作用在颗粒上的流体曳力，利用DEM方法计算颗粒系统的运动受力情况，2者以一定的模型进行质量、动量和能量等的传递，实现耦合。DEM计算每个颗粒所受的外力（流体曳力、重力及碰撞力等），并由此更新颗粒的位置、速度等信息，最后这些颗粒属性以动量汇的形式加到CFD计算中。

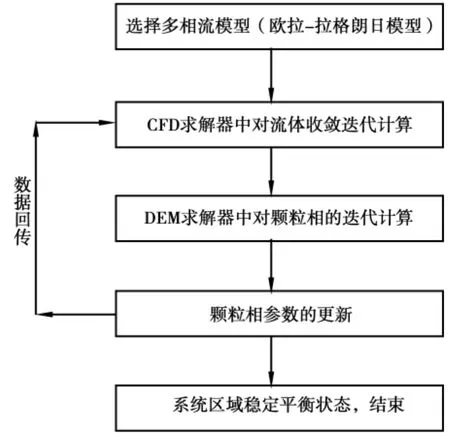
图1 CFD－DEM耦合流程

2 模拟工况

随机结构过滤介质模型和颗粒模型分别如图2、3所示。计算区域中边界条件设置参见文献［1］，即左侧为速度进口，右侧为压力出口，其他的面为对称边界条件，纤维体表面为无滑移边界条件，同时，左侧速度进口设为颗粒释放面，颗粒在释放面上的位置随机生成，并跟随气流向前运动。CFD模型网格数量为55万，残差设定为10－6。为避免伪收敛，同时监控残差和其它变量的变化来判断计算结果是否收敛。进行CFD－DEM 耦合模拟的计算机配置为：CPU i5－23002.80GHz，内存为4G。

图2 过滤介质模型

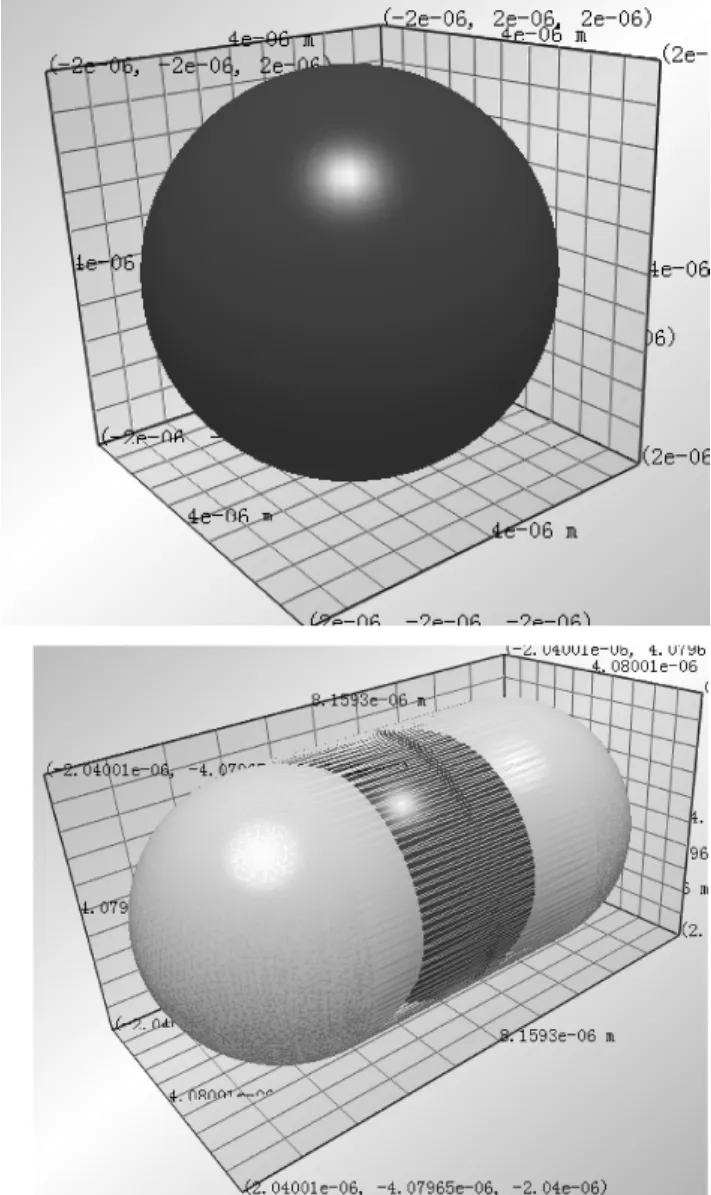
图3 颗粒体系（上为球形颗粒、下为椭球形颗粒）

3 结果与分析

3.1 微细颗粒在纤维介质表面的沉积形式

图4形象的表示了不同形状（球形和椭球形）的非等粒径微细颗粒物在纤维介质表面上的沉积与团聚模拟。可以看出，沉积颗粒并不是均匀的分布在纤维之上，而是成一条凸起树枝状的链状聚集体，沉积在纤维介质迎风面上，并在其背风面上形成不能为后续来流粒子提供沉积的遮挡区域，同时，被捕集的颗粒会堆积并形成树枝状的团聚结构，此时，粉尘颗粒在纤维介质上的沉积并不完全只是纤维 颗粒捕集机制来完成，大量的颗粒捕集是由颗粒 颗粒捕集机制来实现的，这与Kannaoka［15］通过实验观测得出的结论是一致的，这也定性的证明了本文所进行的颗粒在纤维介质上沉积与团聚的模拟研究是较接近真实状况的。

图4 纤维介质表面微细颗粒物的沉积与团聚模拟（Rf＝10～20μm，Rp＝1～10μm，U＝0.3m／s）

3.2 颗粒群特性对纤维介质过滤特性的影响

在实际工程过滤粉尘的应用中，粉尘颗粒的来源并不单一，可能是几种或十几种材质的混合体，颗粒的粒径和形状也并不统一。同时，在运动过程中，由于携带电荷等其他力的作用，颗粒可能会发生碰撞接触而形成较大的团聚体，并且在与纤维介质和已沉积颗粒接触时，反弹力的存在可能将导致其最终会脱离纤维和颗粒的捕集。

图5所示为随机结构过滤介质过滤过程中，不同形状、多分散的微细颗粒物随过滤时间变化的运动及沉积图。可以看出，当纤维介质在清洁状态时，颗粒直接在其表面被捕集，且在过滤中表面过滤为主要作用，大部分的颗粒都是在滤料表面被捕集，同时，部分粒径较小的颗粒会进入滤料的内部，经过深层过滤而被捕集，这与所研究对象的材质、结构等因素有关。随着过滤时间的增加，在纤维介质表面，微细颗粒物会逐渐发生碰撞沉积，并会堆积形成颗粒树枝状沉积物，即粉尘层，阻塞过滤介质中的孔隙，这将导致：后续粉尘颗粒一部分被纤维介质所捕集，同时还会有一部分将被纤维表面上的已沉积颗粒所捕获，即表面过滤，此时，过滤介质的过滤效率会迅速增加并将达到峰值，即最高过滤效率；随着过滤的持续进行，介质中粉尘层越来越厚，此时，内部的介质将丧失捕集颗粒的能力，同时，由于粉尘层的局部可能会发生坍塌、破碎等现象，介质孔隙的堵塞也将更加严重，其运行阻力会急剧增加，而这将导致设备运行费用的增加和介质的破损，增加过滤成本。因此，研究微细颗粒物在过滤介质表面上的沉积形式和团聚结构，合理的优化滤料设计和运行工况参数对实现高效低阻，延长滤料寿命，减少运行成本以及节能减排具有重要的意义。

图5 随机结构过滤介质过滤中颗粒体系的运动仿真（Rf＝10～20μm，Rp＝1～10μm，U＝0.3m／s）

图6所示为介质过滤中某一瞬间T＝0.006s时，不同颗粒体系模型中，不同速度范围内的颗粒数目分布情况。其中，颗粒从控制面上释放时的初始速度为0.3m／s，由于颗粒碰撞、绕圆柱群纤维体的绕流以及介质内部孔隙度的突变，部分颗粒的速度会发生瞬间急剧增大；当颗粒被捕集沉积在纤维或已沉积颗粒上时，沉积的颗粒的速度会降低至零，但由于气流和后续颗粒撞击的作用，颗粒与颗粒间会发生微小的压缩现象，因此沉积颗粒可能会获得一个极微小的瞬间速度。可以看出，接近真实过滤状况的多颗粒体系模型，其捕集颗粒的能力（82%）要优于单一颗粒体系模型的捕集颗粒能力（64%）。这是由于颗粒形状的不规则性，相比球形颗粒其表面积要更大，在运动过程中更容易发生颗粒接触而形成较大的颗粒团聚体，在通过过滤介质时，更容易与介质以及已沉积的颗粒发生接触碰撞而被捕获。因此，分析颗粒体系的组成以及颗粒形状的基础理论研究对发展纤维过滤理论技术和优化过滤介质过滤参数等具有重要的理论意义。

图6 不同速度范围内的颗粒数分布（T＝0.006s）

4 结 论

基于CFD－DEM耦合模拟了纤维过滤过程中气 固两相流动的特性，同时充分考虑了颗粒群的组成、颗粒多分散性、颗粒与颗粒、颗粒与纤维间的反弹作用以及颗粒团聚等影响因素的作用，分析了纤维过滤中颗粒群的运动特性以及粉尘颗粒的沉积形式，结果表明：

1）采用CFD－DEM方法模拟过滤介质的过滤过程以及微细颗粒物在纤维介质表面的沉积过程和沉积形式是方便且可行的，其模拟结果与前人的实验观测结果是基本吻合的。

2）纤维过滤过程中，起主要作用的是表面过滤，大部分的颗粒都是在介质表面被捕集，同时部分粒径较小的颗粒会进入到介质内部，经过深层过滤作用而被捕集。

3）粉尘颗粒在纤维介质上的沉积并不完全只是纤维 颗粒捕集机制，大量的颗粒捕集是由颗粒 颗粒捕集机制来实现的。

4）过滤介质对于不同颗粒体系的微细颗粒物，其过滤性能也有所差别，对于本文的过滤介质模型，多颗粒体系的过滤效率明显高于单一的颗粒体系的过滤效率。

［1］钱付平，王海刚.随机排列纤维过滤器颗粒捕集特性的数值研究［J］.土木建筑与环境工程，2010，32（6）：120－126.Qian F P，Wang H G.Numerical analysis on particle capture characteristics of fibrous filters with random structures ［J］.Journal of Civil，Architectural ＆ Environmental Engineering，2010，32（6）：120－126.

［2］Fu H M，Zhu H.Simulating deposition of aerosol particles on single fiber surface［J］.Journal of Donghua University：English Edition，2009，26（3）：252－258.

［3］Hosseini S A，Tafreshi H V.3－D simulation of particle filtration in electrospun nanofibrous filters［J］.Powder Technology，2010，201（2）：153－160.

［4］Wang H，Zhao H B，Guo Z L，et al.Numerical simulation of particle capture process of fibrous filters using Lattice Boltzmann two－phase flow model［J］.Powder Technology，2012，227（9）：111－122.

［5］Long Z W，Yao Q.Numerical simulation of the flow and the collection mechanism inside a scale hybrid particulate collector［J］.Powder Technology，2012，215－216（1）：26－37.

［6］Fotovati S.Hosseini S A，Tafreshi H V，et al.Modeling instantaneous pressure drop of pleated thin filter media during dust loading［J］.Chemical Engineering Science，2011，66（18）：4036－4046.

［7］Tong Z B，Yang R Y，Yu A B，et al.Numerical modeling of the breakage of loose agglomerates of fine particles［J］.Powder Technology，2009，196（2）：213－221.

［8］Tong Z B，Yang R Y，Chu K W，et al.Numerical study of the effects of particle size and polydispersity on the agglomerate dispersion in a cyclonic flow［J］.Chemical Engineering Journal，2010，164（3）：432–441.

［9］Kempton L，Pinson D，Chew S，et al.Simulation of macroscopic deformation using a sub－particle DEM approach ［J］.Powder Technology，2012，223（6）：19－26.

［10］Tsuji Y，Tanaka T.Lagrangian numerical simulation of plug flow of cohesionless particles in a horizontal pipe［J］.Powder Technology，1992，71（3）：239－250.

［11］赵永志，程易，丁宇龙，等.不同入口结构下行床内气固流动及混合行为的CFD－DEM 模拟［J］.2007，58（6）：1396－1403.Zhao Y Z，Cheng Y，Ding Y L，et al.CFD－DEM simulation of flow and mixing behavior in downers with different entrance structures［J］.Journal of Chemical Industry and Engineering，2007，58（6）：1396－1403.

［12］杨杰程，张宇，刘大有，等.三维风沙运动的CFD－DEM数值模拟［J］.中国科学：物理学、力学、天文学，2010，40（7）：904－915.Yang J C，Zhang Y，Liu D Y，et al.CFD－DEM numerical simulation of three－dimensional sand movement ［J］.Scientia Sinica Phys，Mech ＆ Astron，2010，40（7）：904－915.

［13］卢洲，刘雪东，潘兵.基于CFD－DEM方法的柱状颗粒在弯管中输送过程的数值模拟［J］.中国粉体技术，2011，17（5）：65－69.Lu Z，Liu X D，Pan B.Numerical simulation of cylindrical particles conveying in curved ducts using CFD－DEM coupled approach［J］.China Powder Science and Technology，2011，17（5）：65－69.

［14］胡国明.颗粒系统的离散元素法分析仿真［M］.武汉：武汉理工大学出社，2010.

［15］Kanaoka C.Performance of an air filter at dust－oaded condition［C］.Advance in Aerosol Fltration，2001，323－36.