免疫遗传算法在结构损伤识别中的应用与改进
郭惠勇,李正良
(重庆大学a.土木工程学院;b.山地城镇建设与新技术教育部重点实验室,重庆 400045)
各种工程结构在投入使用后,由于环境的作用,其材料的微观成分就会随着时间的推移而发生演变,其结果导致材料的强度、刚度等力学参数降低,从而在结构上累积起裂缝、腐蚀、变形等损伤。对于重要的桥梁、大坝、河堤、高层建筑等大型结构,以及航空航天领域里的大型航天器和空间站等设备,结构的损伤可能会引起建筑物的倒塌或者航空航天器的坠毁,从而造成巨大的经济和人员生命的损失。因此,对结构损伤的识别研究一直是研究热点[1]。
免疫遗传算法作为一种新型的启发式算法,在很多方面都已有研究应用[2-5],但是在结构的损伤识别领域的应用还未见报道。目前结构的损伤识别研究主要是依靠动力特性的改变进行损伤的定性和定量研究,以及结合遗传算法、神经网络、模糊理论等各种人工智能算法、或者结合小波分析等各种数字信号处理技术来进行损伤识别研究。董聪等[6]分析了各种动力特性指标,如频率变化指标、位移模态变化指标以及曲率模态变化指标,并进行了基于动力特性指标的数值模拟以及试验验证;Shi等[7]提出了应变能变化率指标以及多损伤定位保证准则,并利用该类指标分析了桁架结构的损伤识别问题,刘晖等[8]则进一步提出了模态应变能耗散率指标,其识别效果较应变能变化率指标有了一定程度的提高;邹万杰和瞿伟廉[9]则采用遗传算法和频响函数对一个桁架结构进行了数值模拟,并以测试频响函数和计算频响函数的形状相关系数来构造遗传算法的优化目标函数,在考虑测量噪声的情况下,进行了损伤识别计算;肖仪清和李成涛[10]则采用损伤前后曲率模态的变异特征构造了梁式结构单损伤情况的普适概率神经网络,研究了斜拉桥桥面板损伤识别情况;张力和张瑜[11]则通过模糊模式方法对结构损伤模式进行了识别,并对桥梁Benchmark模型进行了试验验证;管德清和黄燕[12]则采用应变模态的小波变换方法研究了框架结构的损伤识别问题,分别利用了不同类型的小波对应变模态进行小波变换,以及对小波变换系数进行了去噪声处理。Guo和Zhang[13]采用了加权证据理论分析结构的损伤定位问题,但是却没有分析损伤的程度识别问题。虽然上述方法在结构的损伤识别领域已经取得了一定的成果,但是仍存在着一些不足,在损伤识别领域,对于较为复杂结构仍缺少一种稳定、高效的多损伤定性和定量识别方法,基于遗传算法的损伤识别技术容易因未成熟收敛而无法得到最优解,神经网络则需要进行样本训练来确定一些参数,而模糊理论方法以及小波分析方法的识别精度仍需要提高,本文针对以上问题,提出了基于改进免疫遗传算法和贝叶斯融合理论的二阶段结构损伤识别方法。
1 结构损伤的初步定位
对于多损伤问题,单纯采用一种方法可能会使识别结果不稳定或者不能完全识别出所有的损伤位置。因此,采用具有互补性质的2种或2种以上类型数据往往可以获得更好的定位结果。本文主要采用频率数据以及包含位移模态的应变能数据作为2种源数据,再通过应变能耗散率方法和频率识别方法分别获取初步决策,最后通过贝叶斯融合方法获取总的决策和识别结果。
1.1 应变能耗散率方法
先采用文献[6]中的应变能耗散率指标获取第一种损伤定位源数据,其描述如下:
一般来说,结构的损伤常常会降低结构的刚度特性,对质量的影响很小。因此,结构在损伤前后,第j个单元所对应的结构前m阶模态在损伤前后的单元应变能为
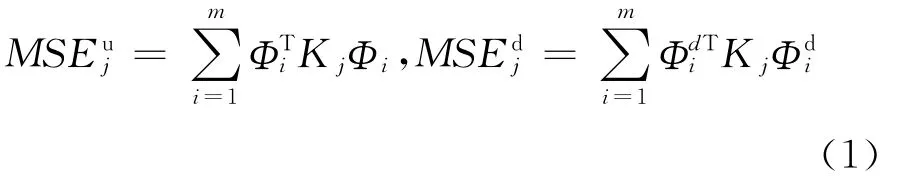
式中:Kj为第j个单元的刚度矩阵;分别为损伤前后结构的第i阶位移模态。由此,可得到第j个单元的损伤因子Cj
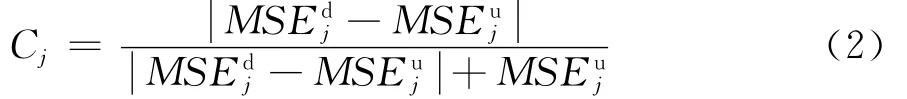
识别时需要计算每个单元的损伤因子值,具有较高损伤因子值的单元往往是更可能的损伤单元。为了后续的融合处理,需要将每个单元损伤因子值进行概率化。
1.2 频率改变识别法
主要采用频率数据及其相应的指标作为第2种损伤定位源数据,其描述如下
考虑到有损结构,则相应的特征方程为
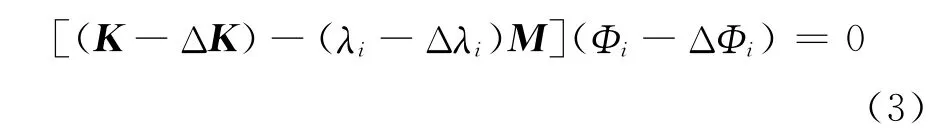
式中:M、K分别为n×n维质量、刚度矩阵;λi为第i阶特征值;Δλi、ΔΦi分别第i阶特征值改变量和位移模态改变量。忽略二阶项,则上式成为
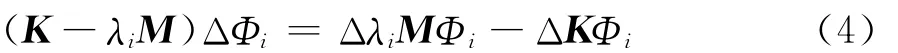

由于矩阵M和K一般是对称阵,利用特征关系(K-λiM)Φi=0,上式成为

可将ΔK表示成为每一个单元矩阵与损伤系数乘积的和[5],即

式中:NE为单元总数;Kk为第k个单元在整体坐标下的矩阵;ck为第k个单元的损伤系数。将(7)式代入(6)式可得
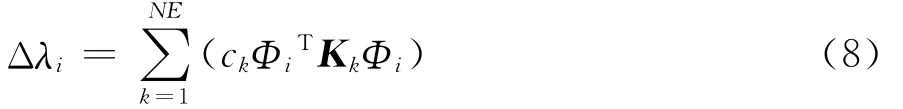
由于实际中需要多个测量频率才能进行识别,故这里考虑有s个测量频率,则上式为

式中:KΦ是s×NE维矩阵;其基本组成是KΦik=ΦiTKkΦi;δC 是损伤系数向量。则

式中:KΦ+是Moore-Penrose广义逆矩阵。在这个解中,具有较高损伤系数值的单元往往是更可能的损伤单元。同样,为了后续的融合处理,需要将每个单元损伤因子值进行概率化。
1.3 贝叶斯融合
这里利用信息融合技术中的贝叶斯融合规则进行信息融合,即将来自于应变能耗散率方法与频率方法的信息进行合成,以获得更精确信息。设系统可能的命题为A1、A2…ANE,当利用某一信息源对系统进行观测分析时,得到的分析结果B,如果能够利用系统的先验知识和信息源的特性得到各先验概率P(Ai)和条件概率P(B/Ai),则利用Bayes条件概率公式,根据该信息源的观测将先验概率P(Ai)更新为后验概率P(Ai/B),如下所示
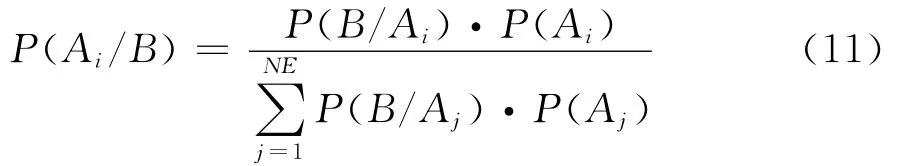
如果假设有t个信息源,观测分析结果分别为B1、B2…Bt时,假设它们之间相互独立,则可以得到系统有t个信息源时的融合的后验概率为
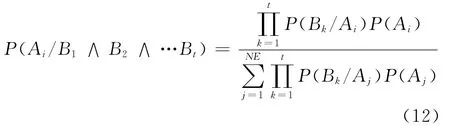
该公式为贝叶斯融合公式。
2 免疫遗传算法定量识别及其改进策略
2.1 免疫遗传算法
免疫遗传算法是借鉴生物免疫系统中抗体的浓度控制原理提出的一种改进的遗传算法,它将求解问题的目标函数对应为入侵生命体的抗原,而问题的解对应为免疫系统产生的抗体。本文是在基于贝叶斯融合初步识别的基础之上,再进行免疫遗传算法损伤定量。即如果已经识别出l个损伤单元,则免疫遗传算法只需要对该l个损伤单元进行损伤程度识别。采用该方法可以大大缩减搜索的空间,具有较好的搜索效率。由于免疫遗传算法在损伤识别领域的应用还未见报道,故这里针对结构的损伤识别问题讨论免疫遗传算法的设计,包含了抗体编码、相似度、抗体浓度、以及作为抗原的目标函数的描述。
2.1.1 抗体编码 在结构的损伤识别研究中,可以采用二进制编码来反映结构的损伤程度,每个单元的损伤可以采用6位或7位二进制编码来表示,如果只考虑中等程度损伤及轻微损伤问题,可采用6-比特串子体,否则可采用7-比特串子体。这里以6-比特串子体为例,假设融合识别已经识别出l个可能的损伤单元,可以利用l个子体来表示损伤程度,即一个固定长度为6位的比特二进制串子体表示一个相应单元的损伤程度,如

这里定义该二进制串的值为百分比值,例如010101表示损伤程度为21%。l个子体表示l个单元的损伤程度,然后将这l个子体合成一个抗体,这样一个长度为6l-位比特的抗体就可以表示l个单元的损伤程度。定义如下

如果是7-比特串子体,其取值范围是0~127%,而真实的损伤程度范围是0~100%,可以规定当染色体中的一个7-比特串子体的值超过了100%,则重新定义它的值为100%。
2.1.2 目标函数(抗原)考虑频率和振型2种数据,采用了如下的目标函数,
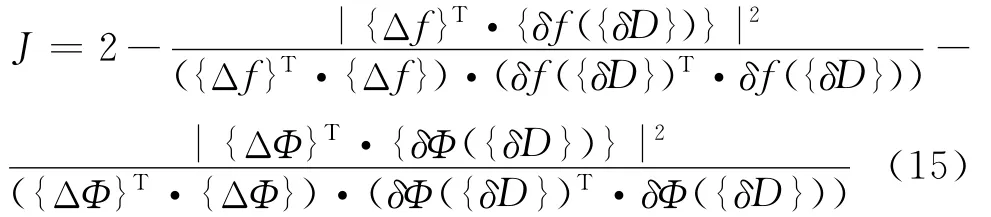
式中:Δf、ΔΦ表示损伤前后频率和位移模态的改变量,如果假设已经识别出l个损伤单元,则δD 是表示在这l个损伤位置处有损伤的变量,其他位置则无损伤;δf表示在这l个位置损伤时的理论计算频率改变值;δФ表示在这l个位置损伤时的理论计算位移模态改变值。该目标函数是最小化问题,要求搜索的解使目标函数最小化。该目标函数由于含有频率和振型2种不同数据,故可以较好的应用于损伤识别研究。
2.1.3 相似度 由于抗体所组成的免疫系统是一个不确定系统,则系统的多样度可由Shannon信息熵来表示。假设免疫系统由N个抗体组成(群体规模为N),每个抗体基因长度为M,则第j个基因的信息熵为:

式中:pij为第i个符号出现在第j个基因座上的概率。则整个群体的平均信息熵为

则2个抗体i和j之间的相似度为

式中:H(2)为抗体i和j的平均信息熵,可由(17)式计算。
2.1.4 基于抗体浓度的个体更新及多样性策略随着进化的发展,群体中抗体的相似度不断的提高,多样性不再保持原有的水平。为了保证抗体的相似度,提高全局搜索能力,防止未成熟收敛,则引人了抗体浓度的概念,即
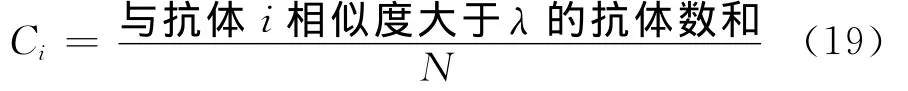
式中:λ为相似度常数,一般取值为0.9≤λ≤1。对于浓度过高的抗体则可以引入新的抗体来增加群体的多样性,以防止不成熟收敛。
2.1.5 遗传操作 主要采用遗传算法中的选择、交叉、变异操作来进行群体更新。这里选择采用轮盘赌方式,并对目标函数进行改造,建立如下适应度函数

式中:J为目标函数。从而将求最小的目标函数转化为求最大的适应度函数,这样可以方便采用轮盘赌选择。交叉可以采用单点交叉方式,变异采用按照概率对抗体基因进行变异的方式。
2.2 一些改进策略
由于基本免疫遗传算法的搜索效率依旧不太高,因此本文提出一些改进策略来提高搜索的效率。
2.2.1 疫苗培养 将每代的一个最优抗体选为疫苗,再对该疫苗进行末位培养,具体是对该疫苗的每个子体的末位数值进行增加或者减去一个步长的调整,调整后的疫苗与原疫苗抗体比较,如果好于原疫苗,则替换为新的疫苗,并直接被保留到下一代,不经过任何的遗传操作。即如果疫苗有l个子体,则依次对这l个子体的最末位数值进行增减一个步长的调整,从而对该疫苗进行末位的微搜索,以更有效地找到最优解。
2.2.2 最优抗体和次优抗体的浓度调节 由于计算每个抗体的浓度和相似度时计算量会过大,而进行进化计算时所有抗体有着向每代的最优抗体靠拢的趋势,则我们只需计算最优抗体和次优抗体的浓度,而不需要计算每个抗体的浓度。如果浓度过高,则在保留部分数目最优或次优抗体的基础上,对多余的最优和次优抗体进行变异操作,
2.2.2 终止条件 这里采用双终止条件。终止条件1:为了避免冗余的迭代,需要选取一个恰当的数w,如果操作群体的群首连续w次不变,则自动判断找到最优解,停止免疫遗传操作。该数既要足够大以保证免疫遗传操作的充分性,又要使免疫遗传操作不产生过多的冗余迭代。终止条件2:如果最优抗体的目标函数的值等于0或者低于某个很小的规定数值,则意味着最优化的解或者较优化的解已经发现,则迭代停止。以上2个条件只要满足任意一个就认为免疫遗传算法已经结束,运行自动停止。
2.3 免疫遗传算法的步骤
本文的免疫遗传算法的具体步骤如下:
1)随机生成初始抗体群,并计算各个抗体的目标函数与适应度。
2)计算抗体的相似度,以及最优抗体和次优抗体的浓度,如果浓度较高,则在保留部分数目最优和次优抗体的基础上,对多余抗体进行变异操作。
3)提取每代抗体的疫苗,然后对疫苗进行培养,即对疫苗的每个子体的末位进行加减一个步长的扫描,以培养出更好的疫苗。
4)进行遗传选择、交叉、变异操作,选择采用轮盘赌方法,交叉采用单点或多位单点交叉方式,变异采用按照概率对基因进行变异的方式。
5)判断是否满足终止条件,如果不满足则重复步骤(2)—(4)。
3 数值计算
考虑如图1所示的一个平面二维铝合金桁架结构。其基本参数为:弹性模量E=72GPa,材料密度ρ=2800kg/m3,杆件长度如图所示,单元截面积为0.001m2。假设有2种多损伤工况,第1种工况,在单元4、18和29发生损伤,刚度分别降低了15%、20%和20%;第2种工况,在单元2、7、26发生损伤,刚度分别降低了20%、10%和15%。首先利用位移模态数据得到应变能法识别结果,再用频率法获得另一结果,并转化为概率化的基本概率值,然后采用贝叶斯融合方法进行初步的损伤定位,最后采用免疫遗传算法进行精确的损伤定位和定量研究。在贝叶斯融合中我们将先验概率值假设为等损伤概率值,当采用免疫遗传算法时,群体规模取800,群首最大迭代次数w为50次,终止条件2的最小值为10-8,交叉概率为0.9,变异概率为0.1,相似度常数λ为0.9,群首浓度概率为0.01。对于第1种工况,采用前15阶频率和前二阶位移模态进行免疫遗传损伤识别,对于第2种工况,采用前10阶频率和第一阶位移模态进行损伤识别。

图1 二维桁架结构图
3.1 例1
当单元4、18、29发生损伤时,计算结果如图2所示。从图2中,可以发现在多损伤情况下,应变能耗散率方法的识别效果较好,但易对单元7发生误判,而频率识别方法的识别结果不理想,易对单元10、26、27、30等产生误判,而采用了贝叶斯融合后,产生了更为理想的识别结果,其识别效果明显好于应变能耗散率方法和频率识别方式,即损伤单元具有更高的损伤基本概率值。这里选取具有较高概率值的单元作为可能的损伤单元,根据贝叶斯识别结果,选取单元3、4、13、18、26、29、30作为可能损伤的单元。
对于这7个可能的损伤单元,利用免疫遗传算法进行定量分析,为了进行对比,分别采用了3种方案:1)含精英策略的简单遗传算法;2)基本免疫遗传算法;3)改进的免疫遗传算法。每种方案均运行10次,计算结果如表1—3所示。从表1中可以发现,含精英策略的简单遗传算法基本可以识别出损伤的单元位置和程度,但是迭代次数较多,意味着搜索效率不高。从表2中可以观察到,当采用免疫遗传算法时,也基本可以识别出损伤的单元位置和程度,其迭代次数相对于简单遗传算法有所降低,意味着搜索效率有所提高。而从表3可以看到,本文的改进方法不仅具有良好的损伤识别效果,而且其收敛速度相比前两种方案均有了较大的提高。从表3的识别结果中可以明显判断出单元3、13、26、30没有发生任何程度的损伤,而对真实损伤的单元4、18、29的识别结果很精确。
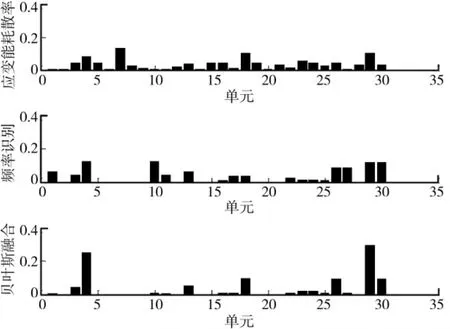
图2 单元4、18、29损伤时的归一化概率值和贝叶斯融合结果
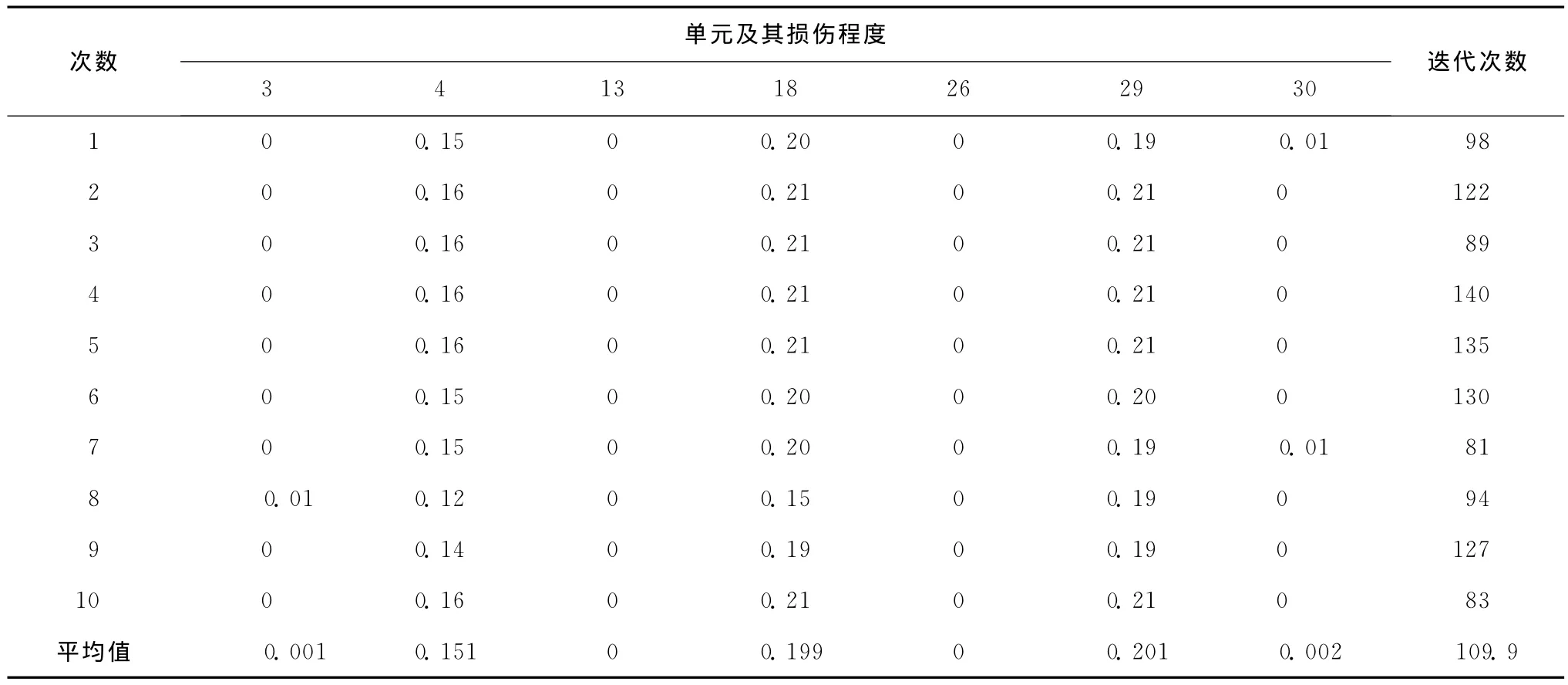
表1 例1的10次简单遗传算法计算结果(含精英策略)

表2 例1的10次基本免疫遗传算法计算结果
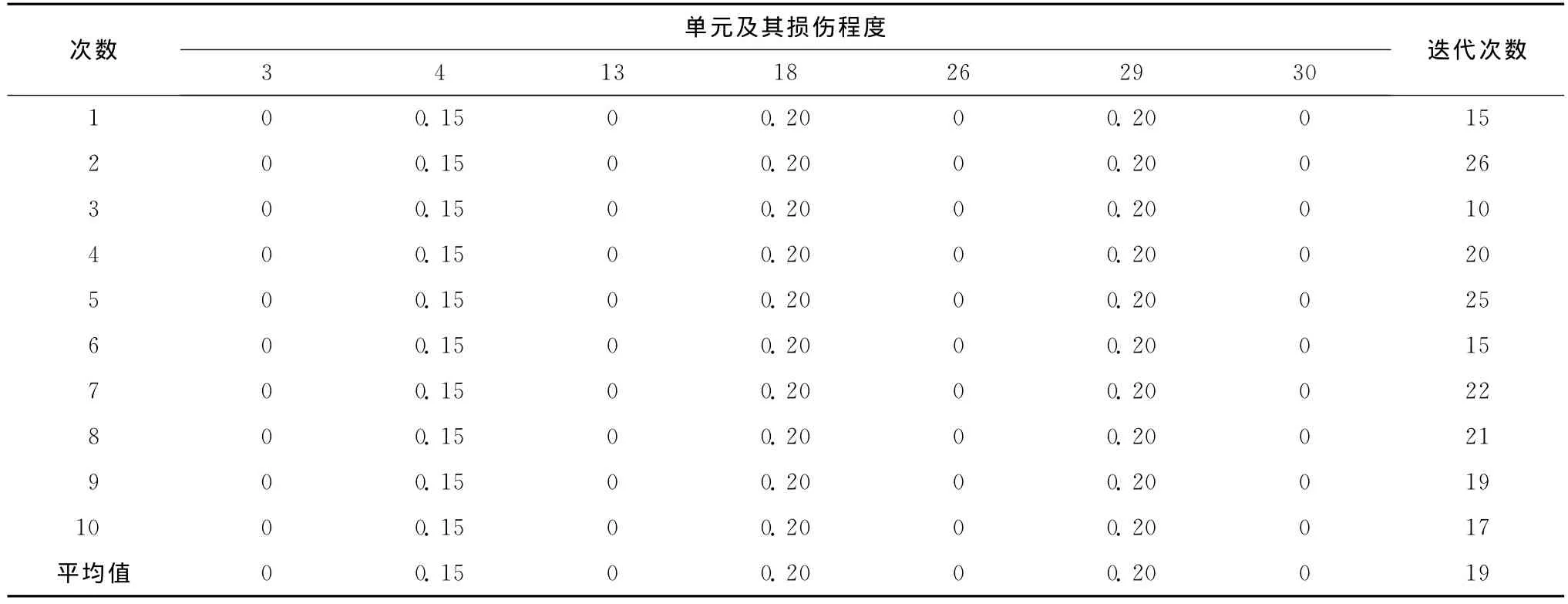
表3 例1的10次改进的免疫遗传算法计算结果
3.2 例2
当单元2、7、26发生损伤时,计算结果如图3所示。从图3中,可以发现在多损伤情况下,应变能耗散率方法的识别效果较好,但易对单元28发生误判,而频率识别方法的识别结果不理想,易对单元12、27等产生误判,而采用了贝叶斯融合后,产生了更为理想的识别结果,其识别效果明显好于应变能耗散率方法和频率识别方式,即损伤单元具有更高的损伤基本概率值。根据贝叶斯识别结果,这里选取单元1、2、4、7、12、26作为可能损伤的单元。
对于这6个可能的损伤单元,利用3种算法进行定量分析,计算结果如表4—6所示。从表4中可以发现,含精英策略的简单遗传算法基本可以识别出损伤的单元位置和程度,但是迭代次数仍旧较多,搜索效率不高。从表5中可以观察到,当采用免疫遗传算法时,也基本可以识别出损伤的单元位置和程度,其迭代次数相对于简单遗传算法有所降低,则意味着搜索效率有所提高。而从表6可以看到,本文的改进方法不仅具有良好的损伤识别效果,而且其收敛速度相比前2种方案均有了较大的提高。从表6的识别结果中可以明显判断出单元1、4、12没有发生任何程度的损伤,而对真实损伤的单元2、7、26的识别结果很精确。
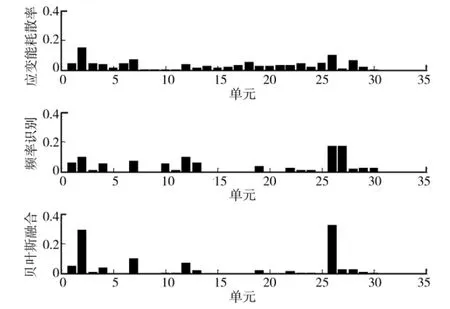
图3 单元2、7、26损伤时的归一化概率值和贝叶斯融合结果
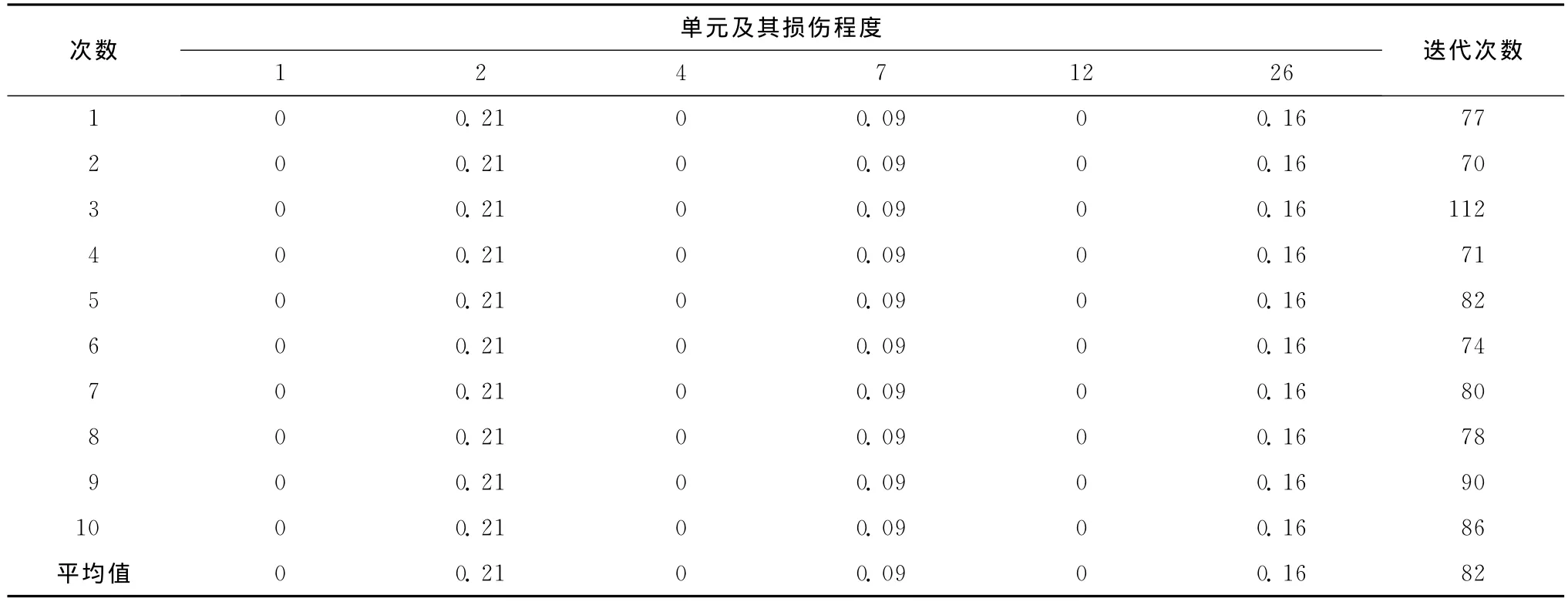
表4 例2的10次简单遗传算法计算结果(含精英策略)
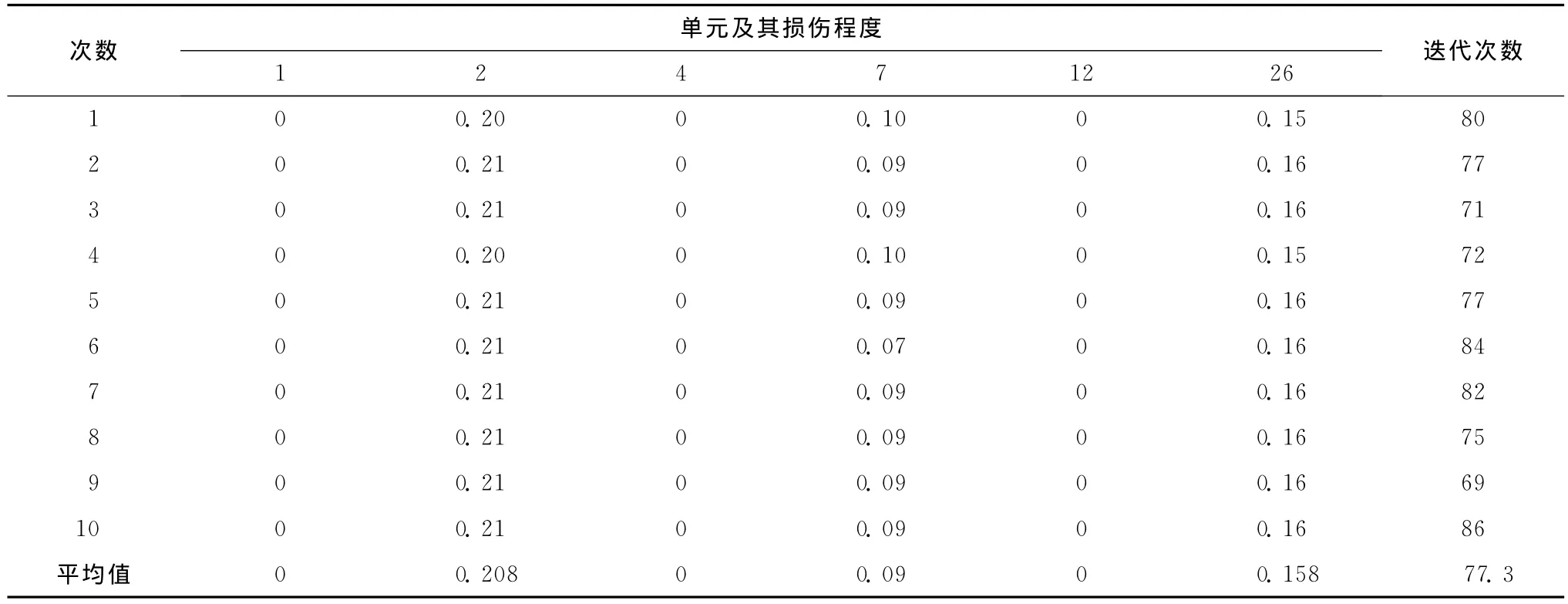
表5 例2的10次基本免疫遗传算法计算结果
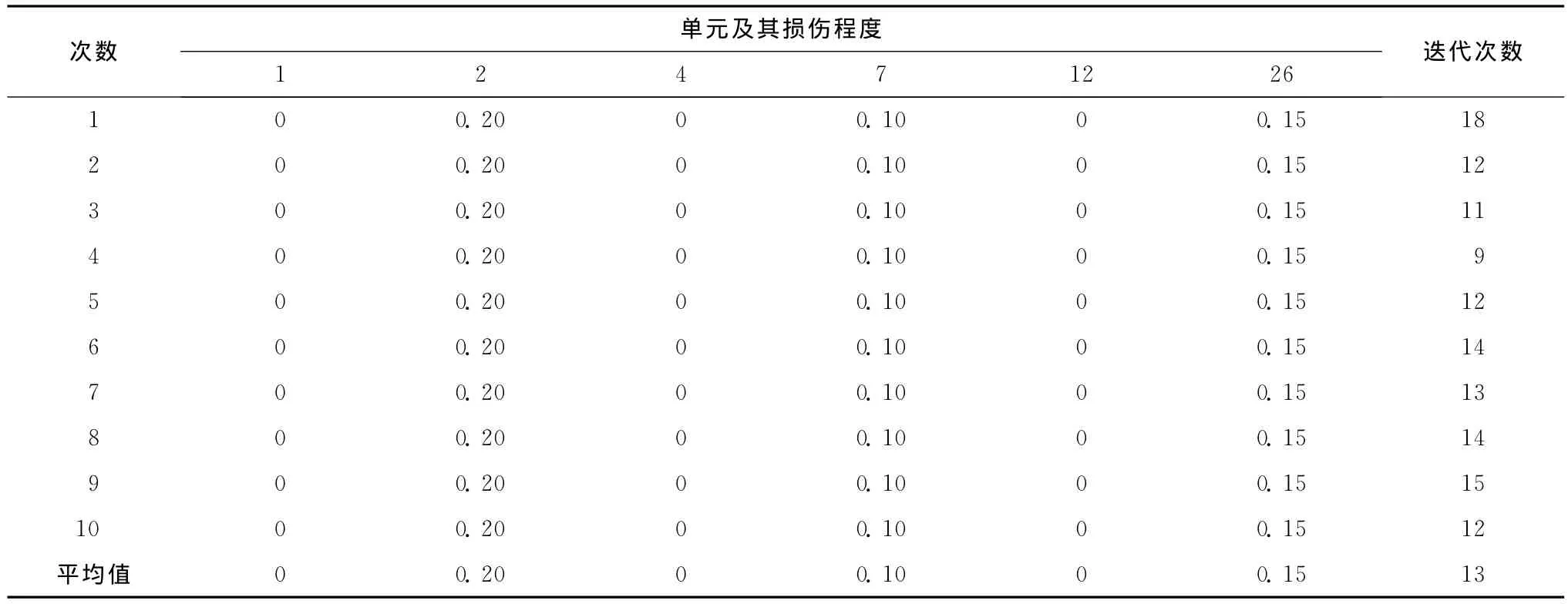
表6 例2的10次改进免疫遗传算法计算结果
由以上2个例子可以发现,将频率和应变能进行融合的贝叶斯理论可以更有效的识别出多损伤的位置,或者决策出潜在的多个有效损伤位置。该方法优于2种单纯使用频率或应变能的频率识别法和应变能耗散率法。而通过对这2种方法的对比(图2、图3),可以发现应变能耗散率法的识别结果要好于频率识别法。同样,对比以上例子的免疫遗传算法损伤定量识别结果,可以发现在一定的群体规模下,基本免疫遗传算法和含有精英策略的简单遗传算法的识别结果较接近,但基本免疫遗传算法的收敛速度要高于简单遗传算法。而采用了疫苗培养等改进策略的免疫遗传算法其不仅识别结果的精度更高,而且收敛速度也有了很大的提高。
文中的方法是一种先定位后定量的分阶段方法,它与单纯使用启发式算法进行搜索的方法相比,可以大大的提高搜索的效率。对于本例中的30单元结构,在识别精度为1%的时候,单纯采用免疫遗传算法等启发式方法,需要在大小为10130≈1.3478(1060的搜索空间中找优化解,而采用先识别定位后免疫遗传定量的方法时,可以大大减少搜索空间,例如对于本文中的例1,只需要在大小为1017≈1.0721(1014的空间内搜索优化解,因此很明显搜索的效率会有很大提高。对于本文例1和例2,如果单纯采用遗传算法或免疫遗传算法等启发式方法,并使用同样的群体规模等免疫遗传参数,几乎找不到理想的识别结果,如果过分增大群体规模和收敛参数,则每一代需要的计算量也就越多,往往会导致一个无法接受的低收敛速率,并且受限制于所具有的计算机硬件条件。
3 结 论
提出了基于免疫遗传算法的两阶段损伤识别方法。该方法首先利用了贝叶斯融合理论来进行损伤的初步定位分析,在此基础上,基于免疫遗传算法进行了损伤的精确定位和定量分析,并提出了疫苗培养等免疫遗传算法的改进策略,通过数值计算和理论分析,可以得出以下结论:
1)如果单纯使用免疫遗传算法等启发式算法进行结构的损伤识别,对于较复杂的结构,由于其相应的复杂单元模型及较多的单元数目,会产生过大的搜索空间,在特定的群体规模下,难于找到优化的解,因此单纯的免疫遗传方法主要适用于简单的结构。
2)采用先融合识别定位后免疫遗传算法定量的方法,首先利用贝叶斯融合理论进行损伤定位,可以得到更精确的损伤位置估计,在此基础上利用免疫遗传算法进行损伤程度的估计,可以有效的进行损伤程度的分析,该二阶段方法不仅大大降低所需搜索的空间,而且搜索效率较高。
3)采用改进的免疫遗传策略,即疫苗培养、最优和次优抗体的浓度调节、以及双终止条件等改进策略,相比于基本免疫遗传算法和简单遗传算法,改进的免疫遗传算法不仅可以较容易找到最优解,而且搜索效率更高。
[1]郭惠勇,李正良,彭川.结构损伤动力识别技术的研究与进展 [J].重庆建筑大学学报,2008,30(1):140-145.GUO HUI-YONG, LI ZHENG-LIANG, PENG CHUAN.Researches and advances in structural damage dynamic identification technology[J].Journal of Chongqing Jianzhu University,2008,30(1):140-145.
[2]WANG D W,RICHARD Y K,FUNG W H.An immune-genetic algorithm for introduction planning of new products[J].Computers &Industrial Engineering,2009,56(3):902-917.
[3]CHEN D C,HSIEH Y C.Using immune-based genetic algorithms for single trader's periodic marketing problem [J].Mathematical and Computer Modelling,2008,48:420-428.
[4]SU Z G,WANG P H,YU X J.Immune genetic algorithm-based adaptive evidential model for estimating unmeasured parameter:Estimating levels of coal powder filling in ball mill[J].Expert Systems with Applications,2010,37:5246-5258.
[5]杨建华,孙钢,吴朝晖.基于免疫遗传算法的卫星天线结构设计 [J].浙江大学学报:工学版,2010,44(4):645-651.YANG JIAN-HUA,SUN GANG,WU ZHAO-HUI.Design of satellite antenna using immune genetic algorithm[J].Journal of Zhejiang University:Engineering Science,2010,44(4):645-651.
[6]董聪,范立础,陈肇元.结构智能健康诊断的理论与方法 [J].中国铁道科学,2002,23(1):11-24.DONG CONG,FAN LI-CHU,CHEN ZHAO-YUAN.Theory and method for structural intelligent health diagnosis[J].China Railway Science,2002,23(1):11-24.
[7]SHI Z Y,LAW S S,ZHANG L M.Structural damage localization from modal strain energy change[J].Journal of Sound and Vibration,1998,218(5):825-844.
[8]刘晖,瞿伟廉,袁润章.基于模态应变能耗散率理论的结构损伤识别方法 [J].振动与冲击,2004,23(2):118-121.LIU HUI,QU WEI-LIAN,YUAN RUN-ZHANG.Structural damage detection method based on the theory of dissipation ratio of modal strain energy[J].Journal of Vibration and Shock,2004,23(2):118-121.
[9]邹万杰,瞿伟廉.基于频响函数和遗传算法的结构损伤识别研究 [J].振动与冲击,2008,27(12):28-30.ZOU WAN-JIE,QU WEI-LIAN.Structural damage identification based on frequency response function and genetic algorithm[J].Journal of Vibration and Shock,2008,27(12):28-30.
[10]肖仪清,李成涛.基于曲率模态和神经网络的斜拉桥损伤识别[J].武汉理工大学学报,2010,32(9):275-279.XIAO YI-QING,LI CHENG-TAO.Damage identification based on wavelet analysis and PNN for cable stayed bridges[J].Journal of Wuhan University of Technology,2010,32(9):275-279.
[11]张力,张瑜.基于模糊理论的结构损伤模式识别[J].西安工业大学学报,2009,29(2):177-183.ZHANG LI,ZHANG YU.Research on damage pattern identification based on fuzzy[J].Journal of Xi'an Technological University,2009,29(2):177-183.
[12]管德清,黄燕.基于应变模态小波变换的框架结构损伤识别研究[J].计算力学学报,2010,27(2):325-329.GUAN DE-QING,HUANG YAN.Damage identification of frame structure by means of wavelet analysis of strain mode[J].Chinese Journal of Computational Mechanics,2010,27(2):325-329.
[13]GUO H,ZHANG L.A weighted balance evidence theory for structural multiple damage localization[J].Computer Methods in Applied Mechanics and Engineering,2006,195(44-47):6225-6238.

