Gumbel分布的基本风压计算与分析

张延年，王元清，张 勇，石永久，李 宁

（1.清华大学 土木工程系，北京 100084；2.沈阳建筑大学 土木工程学院，沈阳 110168；3.沈阳市房地产开发建设管理办公室，沈阳 110013）

统计资料表明，风灾在所有自然灾害中造成的损失最大。其中对建筑物、通信设施、交通设施的破坏更明显[1]。风灾的次数占51.4%，经济损失占40.5%，全球平均每年由于风灾的损失达100亿美元，死亡人数2万人以上[2]。风荷载设防水平的确定是抗风结构设计的战略性决策，定得太高会造成不必要的浪费，定得太低就有可能遇到风险造成重大的损失，这里存在一个最优的设防荷载水平[3－4]。因此，正确地计算和确定各地不同重现期的风压值，对各项建筑工程的抗风安全和建设资金的合理使用都有着重要的现实意义。

多年来关于基本风压的研究相对较少，缺少计算模型的相关研究。另外，多年来中国各地区的最大风速的相关资料不断积累，对其进行统计分析能够更真实反映中国的基本风压情况。因此笔者基于Gumbel分布对中国159个代表性城市在1951—2008年的历年最大风速值进行统计分析并进行参数估算，采用矩法和耿贝尔法分别计算出重现期为10、50、100a的基本风压值，并采用柯尔莫哥洛夫检验法对分布函数进行检验，最后与规范取值进行对比分析。

1 基本风压的计算

采用中国194个国际交换站1951—2008年地面日值数据集中的最大风速年极值资料。风速资料应取自记风速仪的10min平均风速资料，对非自记的定时观测资料需进行时次订正[5]。

式中：y为自记10min平均风速；x为4次定时2min平均风速；系数a，b见表1。

表1 系数a，b取值

则基本风压为

式中：w0为基本风压，kN／m2；ρ为空气密度；v0为重现期为50a的最大风速。

历年最大风速被认为服从Gumbel（极值Ⅰ型）分布[6]，对Gumbel分布的参数估计，通常采用矩法、耿贝尔法和极大似然法。但极大似然法需要用数值求解强非线性方程组，应用起来十分不便[7]，因此采用矩法和耿贝尔法进行参数估计。

1.1 Gumbel分布及参数估计

分布函数

分布密度函数

保证率函数

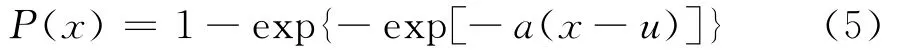
其中a＞0称为尺度参数，u是分布密度的众数。其重现期为R时最大风速为

1.1.1 矩法 参数a、u与矩的关系为一阶矩：E（x）＝＋u，其中γ为欧拉常数，γ≈0.57722。

二阶矩

在实际计算中一般用有限样本容量的均值和标准差作为理论值E（x）和σ的近似估计[8]。

1.1.2 耿贝尔法 假定年最大风压为有序序列x1≤x2≤x3…≤xn，当其分布函数为连续函数时，在第n次观测中位于第i个顺序的观测值的xi期望概率应为，则经验分布函数为

由大数定律，当N → ∞ 时，经验分布F＊（xi）将趋于总体X的极值理论分布函数F（x）。

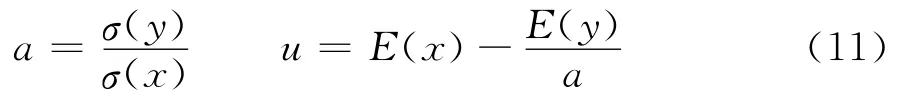
在实际计算中可用有限样本容量的均值和标准差作为E（x）和σ（x）的近似估计[9]。

1.2 计算结果优良性指标检验

用样本数据的经验分布拟合理论曲线分布，该随机变量实际总体分布是否符合所选理论分布模型，需要一客观判定方法[10]。柯尔莫哥洛夫检验法不是分区间来检验根据子样得到的经验分布函数F＊（x）与理论分布函数F（x）之间的偏差，而是对每个点都检验F＊（x）与F（x）之间的偏差，因此该检验法比较精确、简单、实用。柯尔莫哥洛夫拟合适度检验指标[11]：

1）拟合标准差

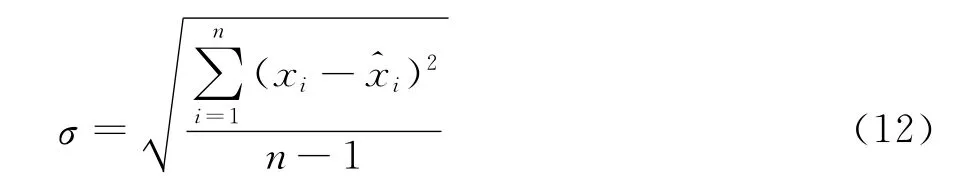
2）拟合相对偏差

式中：xi为有序风速样本；为拟合值。

3）柯尔莫哥洛夫拟合适度

式中：Dn为拟合出来的理论分布与经验分布的最大偏差；F（x）为理论分布函数；（x）为经验分布函数。

由于3种参数估计优良性指标中拟合标准差σ精度最高，拟合相对偏差V和柯尔莫哥洛夫拟合适度Dn的精度相对较低，在比较参数估计的优良性时，以σ最小为优（若σ相等时，再比较V和Dn）。

2 计算结果与分析

利用中国华北地区、东北地区、华东地区、中南地区、西南地区、西北地区6大区域具有代表性的159个城市在1951—2008年58年间的历年最大风速值，采用Gumbel分布进行统计分析并对其参数进行估算。用矩法和耿贝尔法分别计算出重现期为10、50、100a的基本风压值，部分代表城市列于表2。

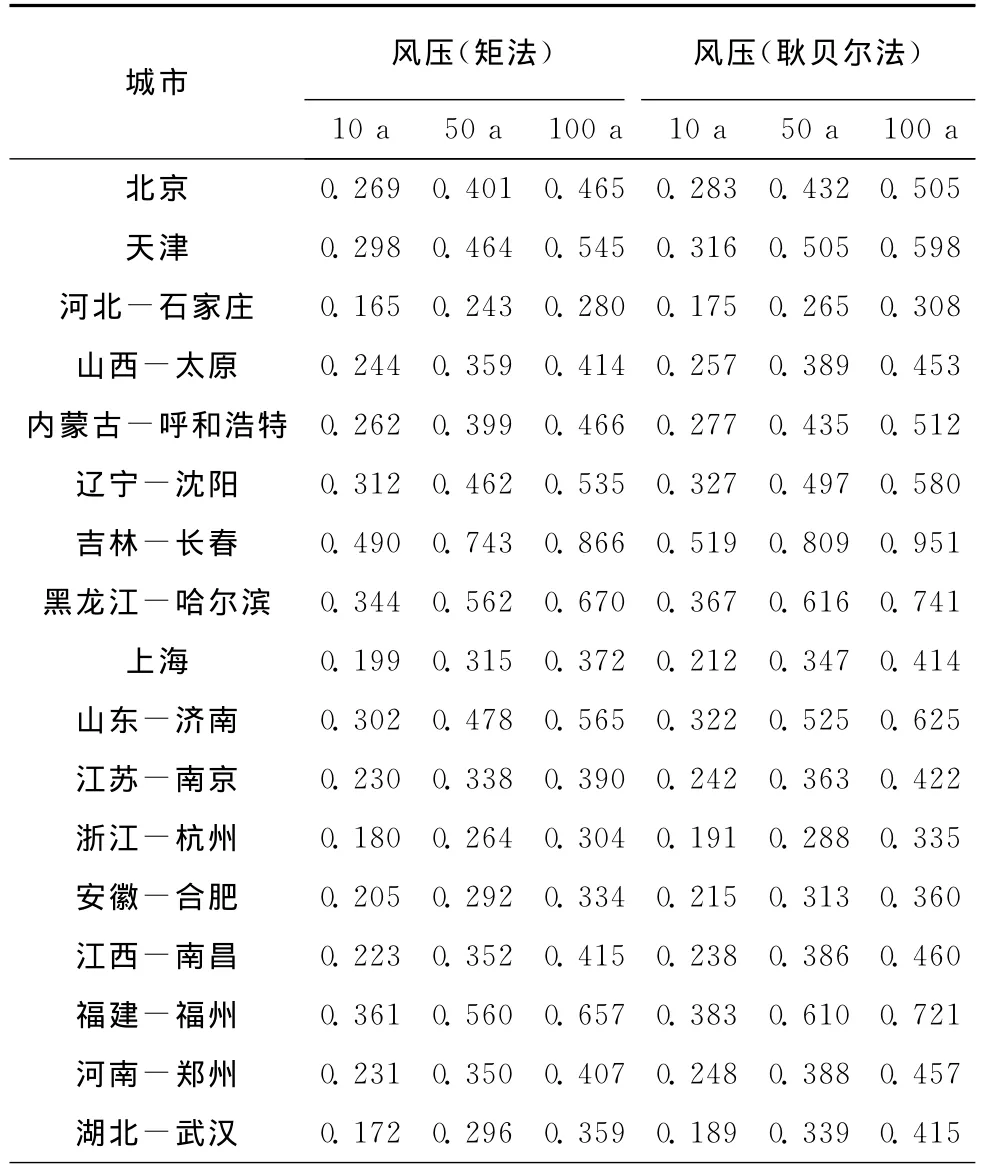
表2 基本风压计算结果 kN·m－2

续表2

采用柯尔莫哥洛夫检验法计算参数估计优良性指标，部分代表城市计算结果见表3。

计算结果表明，以耿贝尔法估计为优的城市有144个，而以矩法估计为优的城市只有15个，耿贝尔法估计明显好于矩法估计；当用Gumbel分布对中国各地区的最大风速年极值进行统计时，应选取耿贝尔法作为Gumbel分布的参数估计方法。

用计算出的基本风压值与规范的基本风压标准值相比，重现期为10a的基本风压对比图如图1所示。表明二者存在显著差异，浙江衢州二者相差0.234kN·m－2，平均相差0.08kN·m－2。

图1 重现期为10a的基本风压对比

重现期为50a的基本风压对比图如图2所示。表明二者存在显著差异，浙江衢州二者相差0.452 kN·m－2，平均相差0.11kN·m－2。

图2 重现期为50a的基本风压对比

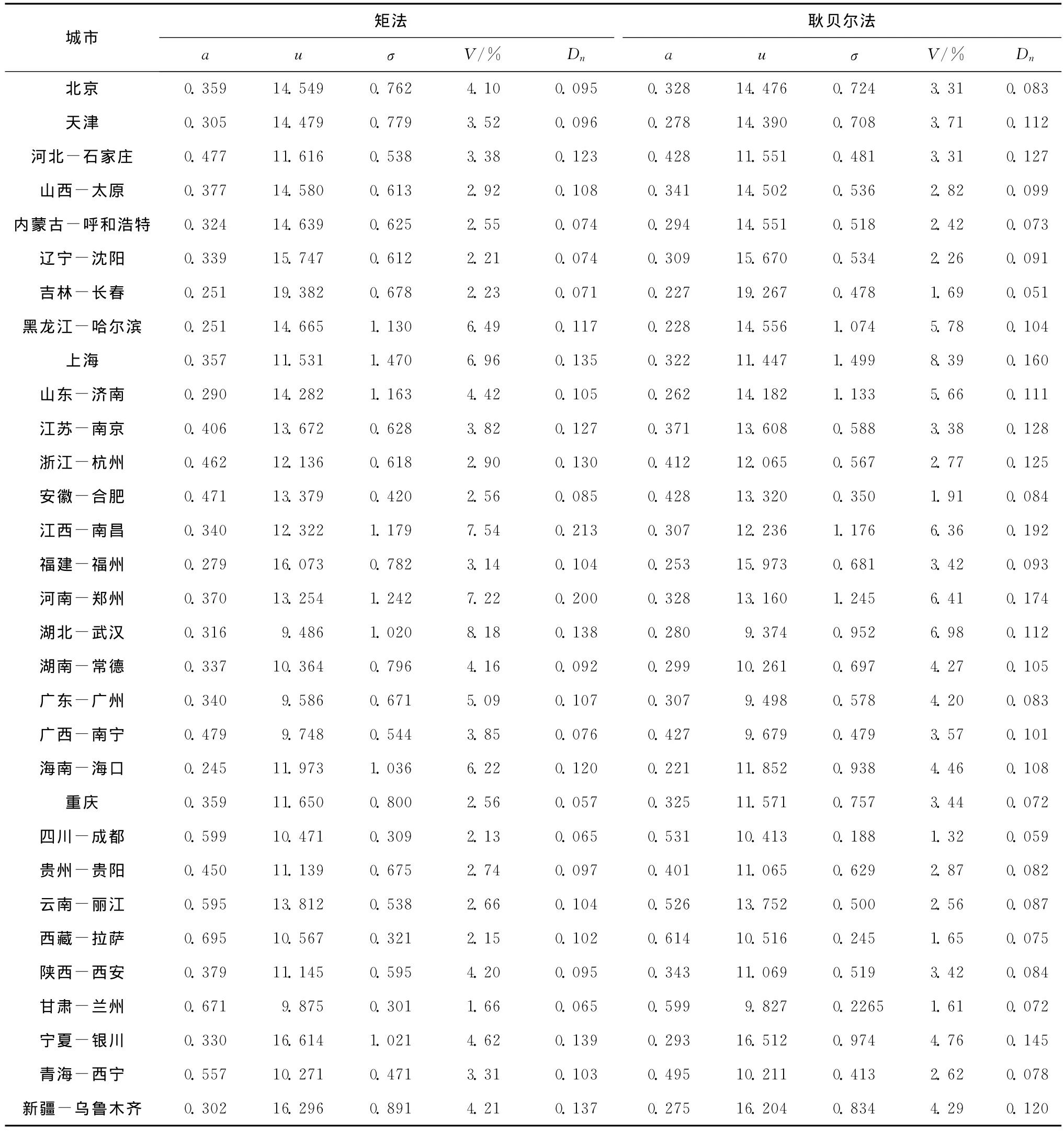
表3 参数估计优良性指标的计算结果

重现期为100a的基本风压对比图如图3所示。表明二者存在显著差异，浙江舟山二者相差0.538 kN·m－2，平均相差0.13kN·m－2。

图3 重现期为100a的基本风压对比

重现期为10、50、100a的基本风压值对比分析表明，《建筑结构荷载规范》（GB 50009）的风压计算的采样数据少，与采用近58a间的历年最大风速值计算的基本分压相比存在较大差异，表明规范取值已经不能真实反映我国的基本风压情况，建议进行相应修订。

3 结 论

通过对中国159个城市58a间的历年最大风速值进行统计分析，分别计算出重现期为10、50、100a的基本风压值，得出以下结论：

1）当采用Gumbel分布对中国各地区的最大风速年极值进行统计时，耿贝尔法比矩法拟合效果好，选取的参数估计方法应以耿贝尔法为优。

2）重现期为10、50、100a的基本风压值对比分析表明，《建筑结构荷载规范》（GB 50009）的风压计算的采样数据少，与采用近58a间的历年最大风速值计算的基本分压相比存在较大差异，表明规范取值已经不能真实反映我国的基本风压情况，建议进行相应修订。

[1]NAESS A.Estimation of long return period design values for wind speeds[J].Journal of Engineering Mechanics，1998，124（3）：252-259.

[2]黄本才.结构抗风分析原理及应用 [M].上海：同济大学出版社，2001.

[3]EDMUND C C.Field measurement and experimental study of wind speed profile during thunderstorms[J].Journal of Wind Engineering and Industrial Aerodynamics，2004，92（1）：275-290.

[4]WANG B，ETHERIDGE D W，OHBA M.Wind tunnel investigation of natural ventilation through multiple stacks，Part 1：Mean values[J].Building and Environment，2011，46：1380-1392.

[5]中华人民共和国国家标准.GB 50009—2001建筑结构荷载规范[S].北京：中国建筑工业出版社，2001.

[6]黄浩辉，宋丽莉，植石群.广东省风速极值I型分布参数估计方法的比较 [J].气象，2007，33（3）：101-106.HUANG HAO-HUI，SONG LI-LI，ZHI SHI-QUN.Comparison of estimation of wind speed extreme-I distribution parameters in Guangdong province [J].Meteorological Monthly，2007，33（3）：101-106.

[7]段忠东，周道成.极值概率分布参数估计方法的比较研究 [J].哈尔滨工业大学学报，2004，36（12）：1605-1609.DUAN ZHONG-DONG，ZHOU DAO-CHENG.A comparative study on parameter estimate methodfor extremal value distribution[J].Journal of Harbin Institute of Technology，2004，36（12）：1605-1609.

[8]SALAR E A，GHORANNEVISS M，EMAMI M.Comparative measurements of plasma position using multipole moments method and analytical solution of grad-shafranov equation in IR-T1tokamak[J].Journal of Fusion Energy，2009，28（4）：385-389.

[9]SERKANÖ，YUSUF B，HAKANÇ.A quantitative appraisal of earthquake hazard parameters computed from Gumbel I method for different regions in and around Turkey[J].Natural Hazards，2008，47（3）：471-495.

[10]张延年，张勇，王元清.辽宁省基本雪压的计算与分析[J].华南理工大学学报，2010，38（9）：108-112.ZHANG YAN-NIAN， ZHANG YONG， WANG YUAN-QING.Calculation and analysis of basic snow pressure value of Liaoning province[J].Journal of South China University，2010，38（9）：108-112.

[11]ZHANG C L，FAN J H.An X-ray luminosity analysis for FRIs and FRIIs[J].Science in China Series G：Physics Mechanics and Astronomy，2009，52（9）：1434-1441.