不同配筋率钢筋混凝土柱应变率效应

许 斌，唐 亮，龙业平

（湖南大学 a.土木工程学院；b.建筑安全与节能教育部重点实验室，湖南 长沙 410082）

早在20世纪初，人们就通过试验发现混凝土强度与应变速率有关，混凝土是一种率敏感材料。1917年，Abrams在对混凝土试块进行动载（应变速率约为2×10－4／s）和静载（应变速率约为8×10－6／s）压缩试验时发现混凝土抗压强度存在速率敏感性[1]。随后，人们逐步开展了混凝土在动力荷载作用下的力学性能试验研究。1991年，Bischof和Perry对加载速率对混凝土抗压强度影响的相关研究成果进行了总结，认为在大多数情况下，混凝土动力强度的增长都可以用荷载速率（或应力速率、应变速率）比的对数关系来加以表示[2]。这一结论得到后来研究者 Malvar和Ross的确认[3]。Cotsovos和Pavlovic基于现有混凝土材料在不同应变率水准下的本构试验的结果，运用有限元方法对混凝土动力强度随着荷载速率的增加而增长进行了数值模拟，并对应变率效应的成因进行了探讨[4－6]。

近年来人们在混凝土构件层次上，对应变率对结构构件性能的影响进行了一些模拟和试验研究。研究表明钢筋混凝土结构或者构件在动力和静力荷载作用下的力学行为存在差异。Otani等人对钢筋混凝土梁进行的静力和动力试验发现在地震的应变率水平下，梁的抗弯承载力较静态的抗弯承载力提高7%～20%[7]。Tagami等人通过对钢筋混凝土柱的动力和静力试验发现在动力加载下柱的抗弯承载力和抗剪承载分别比静力加载下提高6.9%～9.5%和11.3%[8]。Cotsovos等人通过有限元模拟发现随着加载速率的增大，混凝土梁的刚度和承载力提高，而加载点的最大位移则出现降低[9]。然而，由于土木试验加载设备的技术限制，现阶段典型钢筋混凝土构件快速加载条件下的相关的试验研究成果仍显不足。

钢筋混凝土柱作为土木工程结构中主要的承重构件，它的失效会导致结构系统的整体坍塌。大量的震害调查表明一些钢筋混凝土结构在地震作用下并没有以设计所期望的强柱弱梁的方式破坏或失效[10]。在汶川地震中，一些混凝土结构中的柱子先于梁破坏而导致了结构的整体坍塌，这在现行的抗震设计思想中是应该避免的。而在另外一些地震中，例如墨西哥地震和土耳其伊斯坦布尔地震，人们也发现大量钢筋混凝土柱的破坏模式不同于预先设想的情况。

我国现行的抗震设计规范并没有充分考虑应变率对材料本构关系以及结构构件的承载能力、变形、耗能能力和破坏模式的影响。在材料的本构关系模型中考虑应变率的影响，对把握钢筋混凝土构件或结构在动力荷载下的力学行为具有至关重要的作用。发展动力荷载下钢筋混凝土构件力学行为模拟的方便可靠的精细化方法非常重要。近年来，我国开始了钢筋混凝土梁柱等典型构件在快速加载下行能的试验和数值模拟研究，对应变率效应以及不同的动力本构模型进行了比较[11]。

笔者提出了一种基于平截面假定并考虑应变率效应的混凝土动力本构的纤维模型来模拟钢筋混凝土柱的动力性能的方法，并利用动力纤维单元模型模拟了本课题组进行的快速加载试验中的4根钢筋混凝土柱在不同加载速率下的单调动力性能。在试验应变率水平下，模拟结果与试验结果的比较表明预测的水平承载力和变形曲线与试验结果吻合较好，验证了模型的有效性。最后，采用验证后的纤维模型研究了不同纵向配筋率和体积配箍率对钢筋混凝土柱动力性能的影响，结果表明纵向配筋率和体积配箍率对动力性能的影响呈现出不同的特征。

1 考虑应变率的动力纤维单元模型

1.1 钢筋混凝土柱纤维模型分析

对于二维钢筋混凝土柱，纤维模型中引入曲率φ和轴向应变εco两个变量。图1描述了一种理想纤维模型。曲率、应变和力的关系如式（1）～（3）式所示。

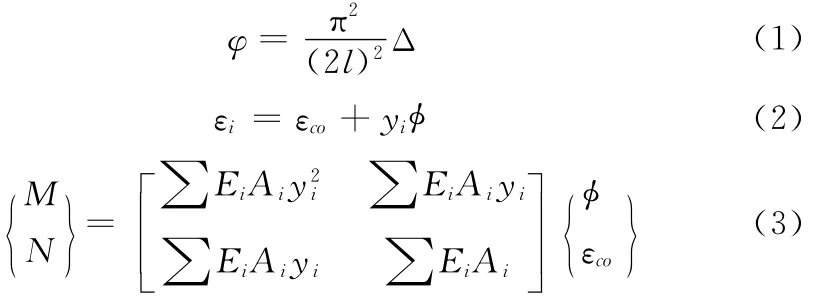
在分析过程中采用了纤维单元模型基本假设和柱子的挠曲线为正弦半波的假定[12]。弯矩 曲率 力的关系可以用纤维模型通过以下分析步骤得到：1）根据柱顶位移（△），计算出柱底截面曲率（φ）；2）利用假定截面重心处的初始应变（εco）求出混凝土条带的应变（εci）、应力（σci）和钢筋的应变（εsi）、应力（σsi）；3）计算出轴力（N）和弯矩（M）；4）检验轴力是否满足平衡条件：

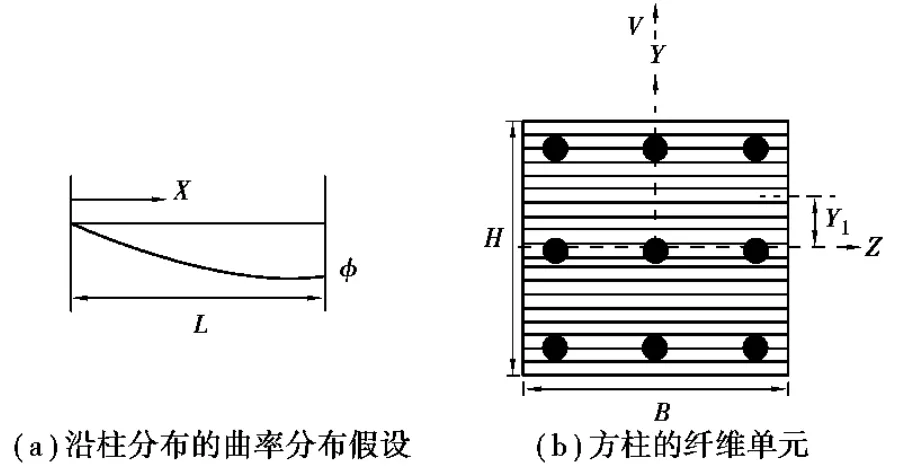
图1 轴压和y方向侧向加载作用下的混凝土方柱截面纤维模型

△1为轴力误差控制参数；Nk为施加的轴力；N为计算出的轴力。如果方程（4）不满足，修正εco的大小并且重复；如果方程（4）满足，计算出侧向力（P）。检验混凝土的受压应变：

如果方程（5）满足根据给定的柱顶位移（△），计算出柱底截面曲率（φ）并转入（2）；如果不满足则停止计算。

在第（2）步计算混凝土应力时，在动力计算时考虑应变率的影响。考虑的方法是用这一迭代步的混凝土应变减去上一迭代步的混凝土应变得到应变差，再根据这一迭代步加载的增量位移除以加载速率得出这一迭代步的加载时间，然后用应变差除以加载时间即可得应变率再代入相关的公式即可得到混凝土的动态应力。

根据以上步骤，利用Fortran语言编制了纤维模型程序并用来计算不同加载速率下混凝土柱的动力行为。

1.2 混凝土本构模型

钢筋混凝土结构中横向钢筋约束混凝土的横向变形，提高轴向抗压承载力。为了考虑方形箍筋的约束作用，在单轴混凝土本构关系[13]基础上采用了Park提出的静力约束混凝土本构模型[14]，它可以由方程（5）表示。式中σc和εc是受压应力和应变，fc和ε0是峰值应力和应变，εco是极限应变。

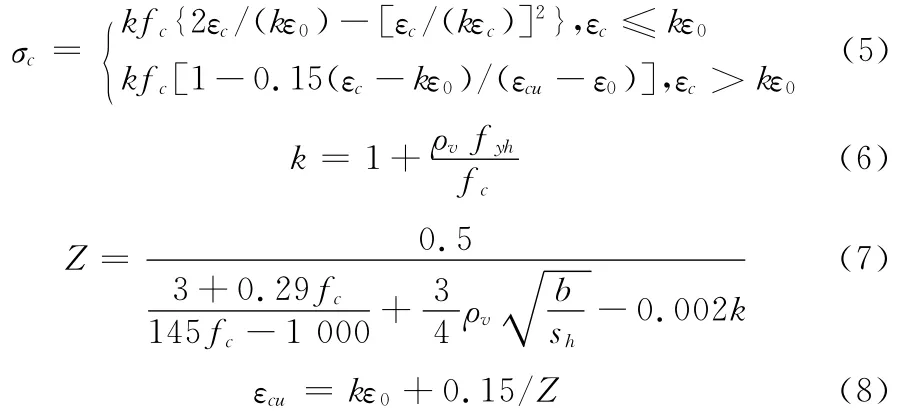
在方程（6）～（8）中；ρv为体积配箍率；fyh为箍筋屈服强度；b为侧向力加载方向混凝土核心的宽度；sh为轴向箍筋间距。

由于混凝土的抗拉强度远小于抗压强度，因此笔者忽略了混凝土抗拉强度的影响。

当结构或者构件承受强震或强风等动力荷载时，需考虑加载速率对混凝土本构关系的影响。笔者混凝土动力本构模型采用了CEB规范建议的考虑应变率影响的模型[15]。

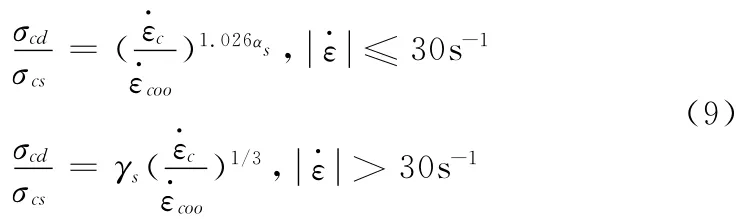
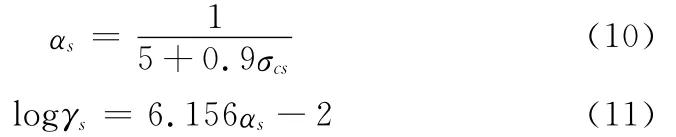
其中σcd为动力受压强度；σcs为静力受压强度；为应变率；的值取3×10－5s－1。

1.3 钢筋本构模型

笔者中钢筋的受拉和受压本构模型近似取为双折线模型[16]，模型可以表示为

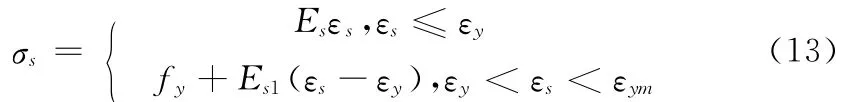
其中σs和εs为钢筋应力和应变；Es为弹性模量；εy为屈服应变；fy为屈服强度；Es1为屈服后上升段的斜率，其值为0.01Es；εym为钢筋极限应变。现有研究表明钢筋对加载速率不敏感，因此本文采用上述的本构模型来模拟动力加载下钢筋混凝土柱的性能。钢筋本构模型如图3所示。

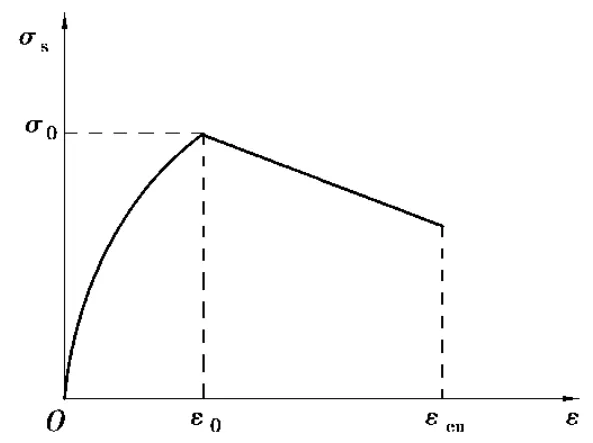
图2 混凝土受压应力应变关系

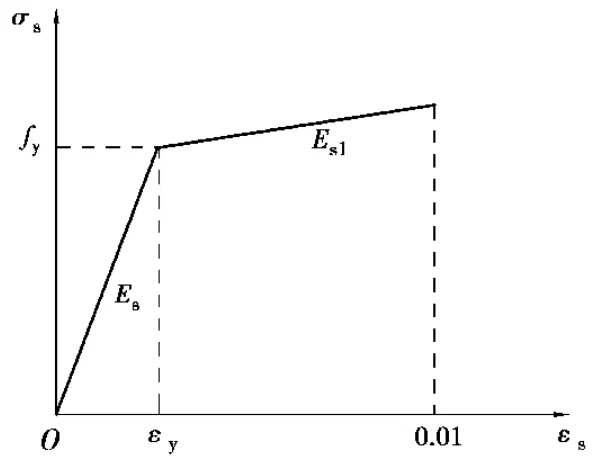
图3 钢筋的应力应变关系

2 模型验证和参数分析

2.1 试件介绍

笔者主要以本课题组进行的钢筋混凝土柱快速加载试验中4个不同配筋率柱构件为研究对象，来验证考虑应变率效应的钢筋混凝土柱纤维模型的有效性。

本课题组快速加载混凝土柱试件采用的是悬臂柱模型，以模拟框架柱性能。试件配筋构造和尺寸参数如图4所示，表1则详细地列举了试件相应的参数。其中，纵向钢筋的保护层厚度是25mm，纵筋的屈服强度为380MPa，箍筋的屈服强度为588MPa，混凝土立方体抗压强度为fc＝59.7MPa。本次试验采用63t德国申克作动器施加快速水平力，100t液压千斤顶施加竖向恒定轴力，力 位移曲线则由申克电液伺服系统采集得到。试验加载装置如图5所示。

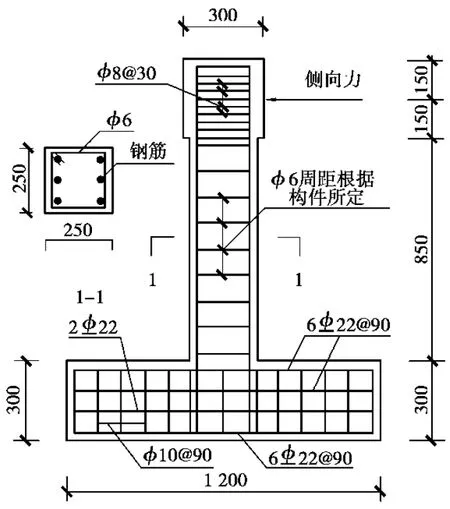
图4 试件的形状和尺寸（单位：mm）

图5 试验加载装置

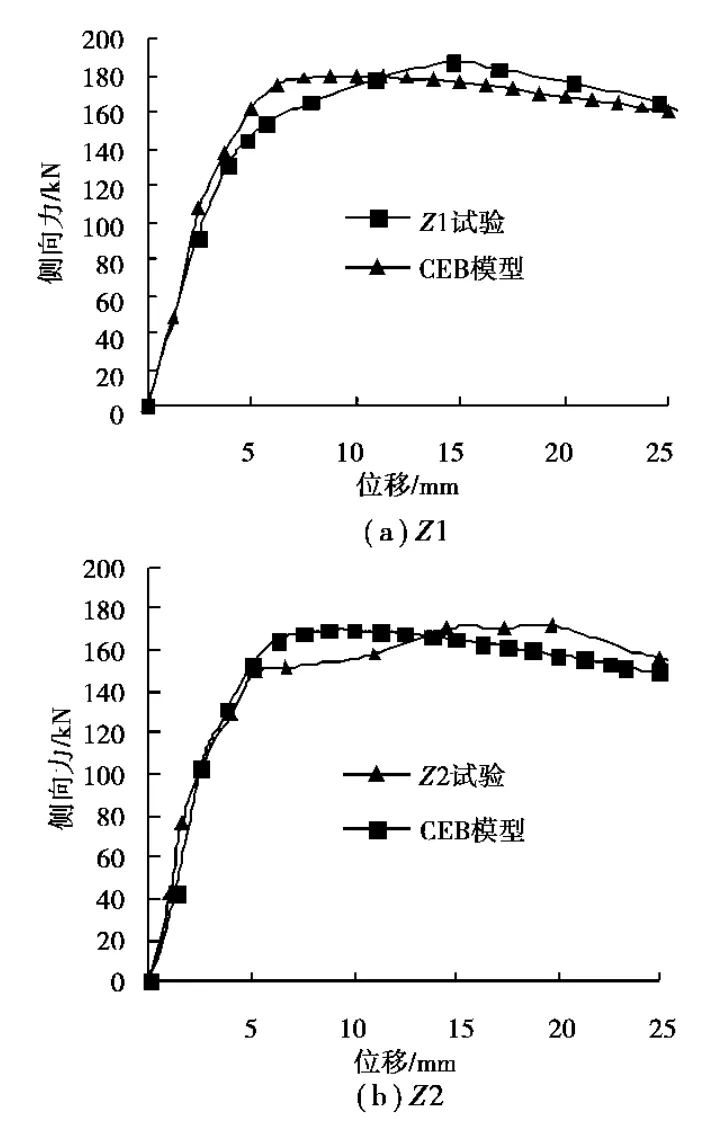
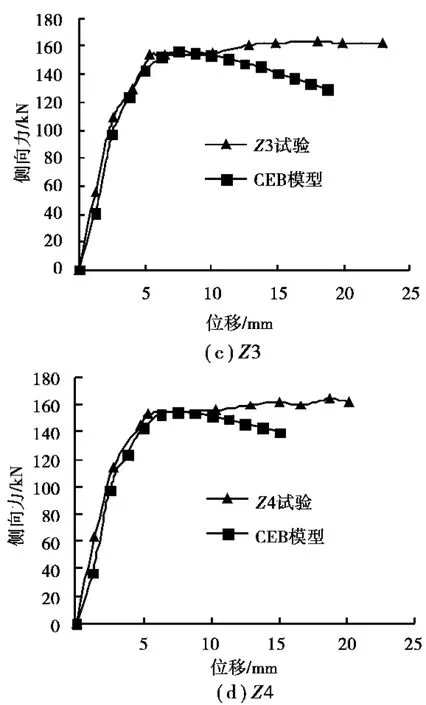
图6 试验和纤维模型模拟的力与位移关系比较

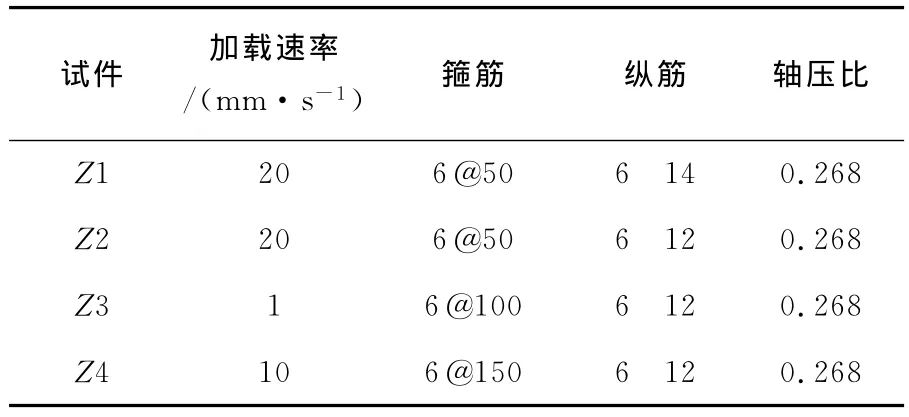
表1 试件性能

2.2 数值模型验证

为了验证考虑加载速率的纤维模型的有效性，笔者对表1中4个不同配筋率柱构件进行了数值模拟，并将模拟的结果和试验结果进行了比较。在本课题组试验研究中，整个快速加载过程通过德国申克电液伺服系统控制实现了不同的加载速率，试件Z1、Z2、Z3和Z4的加载速度分别为0.02、0.02、0.001、0.01m／s。

图6（a）（b）（c）（d）分别表示的是柱Z1、Z2、Z3和Z4数值模拟结果和试验结果的力与位移的关系的比较。从图中可以看到，模拟得到的承载力和变形能力都与试验较为接近。Z1、Z2、Z3和Z4模拟得到的最大承载力与试验分别相差4.1%、0.61%、4.4%和6.13%。可见，基于本文所采用的CEB动力本构模型并运用纤维模型可以较为准确地模拟钢筋混凝土柱在所研究的应变率范围内的恢复力特性。

在纤维单元模型中，构件的延性与计算终止条件或者破坏判据有关。本模拟是以钢筋混凝土柱最外边纤维条带达到混凝土极限应变作为计算停止条件的。Fu等总结前人的研究得出混凝土破坏时的极限应变并没有随着应变率的增加而一致增加或者减少[17]。因此笔者不考虑动态加载对混凝土的极限应变的影响。

2.3 采用考虑应变率效应的纤维模型参数模拟

笔者采用考虑应变率影响的混凝土本构关系的纤维模型主要研究了Z2试件在不同加载速度下的动力性能，并研究不同纵向配筋率和体积配箍率对钢筋混凝土柱动力性能的影响。

图7展示了Z2柱试件在加载速率从0.2mm／s到200mm／s范围内不同纵向配筋率下的力与位移关系。在对快速加载试验的应变分析中，发现加载速率为20mm／s和10mm／s时，最大平均应变率达到了10－3μ／s量级，而1mm／s加载速率则达到了10－4μ／s量级。0.002m／s可以认为是静力加载。从图中可以看出，在力 位移关系的上升段，加载速率的影响较小，随着力的提高，影响越明显，而且加载速率并不改变荷载变形曲线的形态。

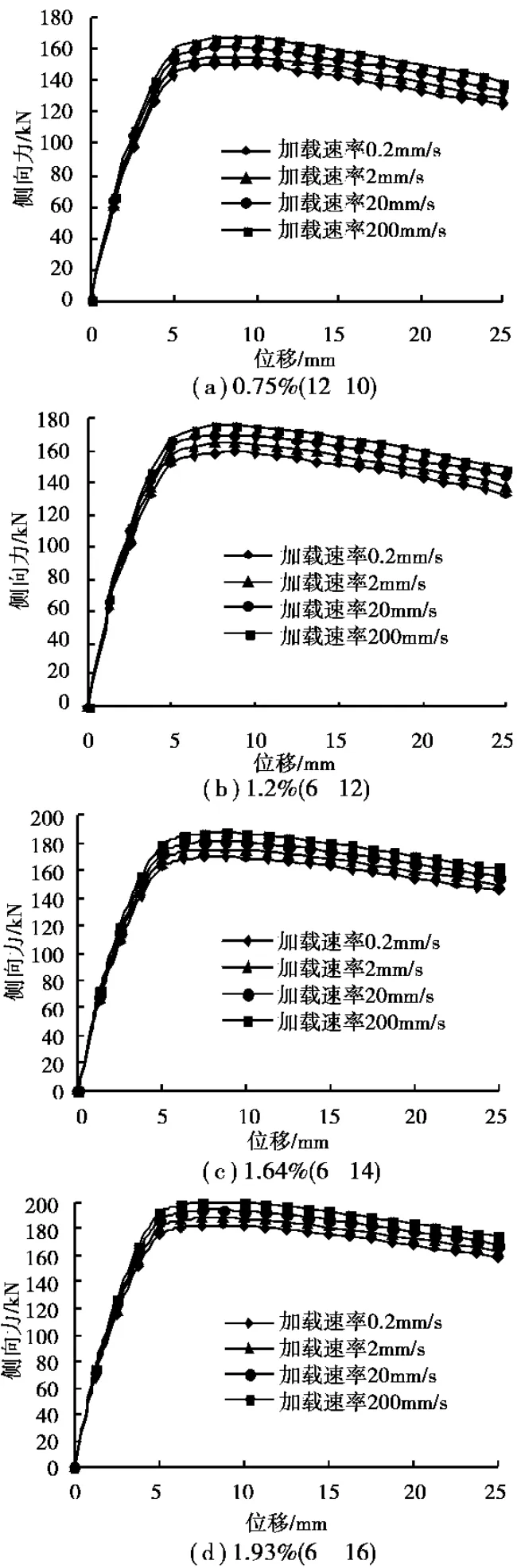
图7 不同纵向配筋率下的力与位移曲线

表2列举了钢筋混凝土柱Z2在不同纵向配筋率下最大动力承载力增长率。从表中可以看出，随着加载速率的增加，试件的最大承载力在各个纵向配筋率下都有不同程度的提高。表中结果也显示了高纵向配筋率试件的动力最大承载力相对增长率比低纵向配筋率试件的要小。

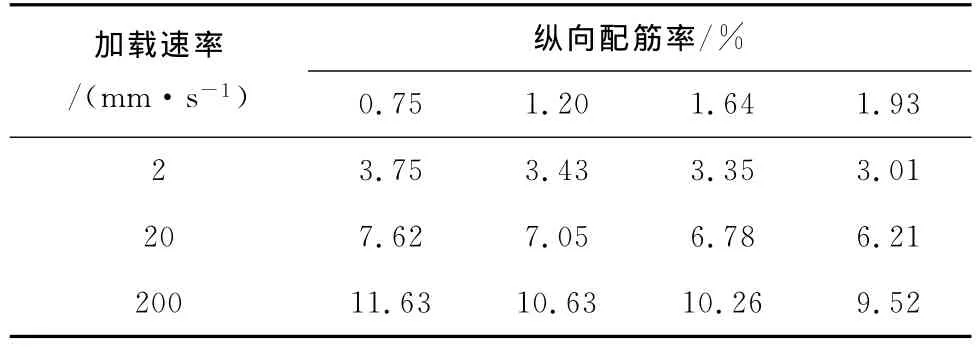
表2 钢筋混凝土柱在不同纵向配筋率下动力承载力增长率

图8展示了Z2试件在加载速率范围从0.2mm／s到200mm／s时体积配箍率对柱子动力性能的影响。从图中可以看出，随着加载速率的增加，柱最大承载力在各个体积配箍率下都有不同程度的提高。表3表示了钢筋混凝土柱Z2在不同体积配筋率下最大动力承载力增长率，最大有10.96%的增长，最小也有3.40%的增长。结果显示了低体积配箍率试件的动力最大承载力相对增长率比高体积配箍率试件的要小。关于柱子的变形能力，可以从图中可以发现，体积配箍率的增加有利于柱子的延性的增加，而在本数值模拟过程中，由于没有考虑加载速率对混凝土极限应变的影响，所以数值模拟结果中加载速度对延性并没有什么影响。

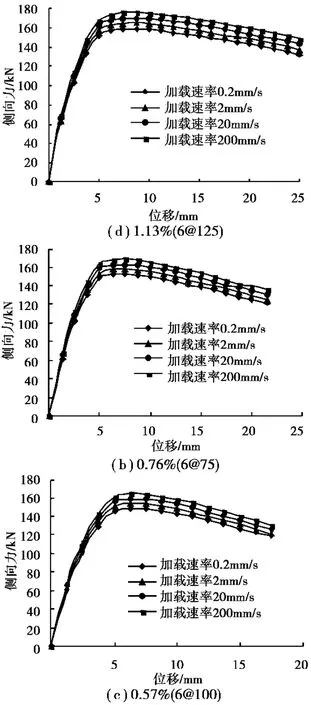
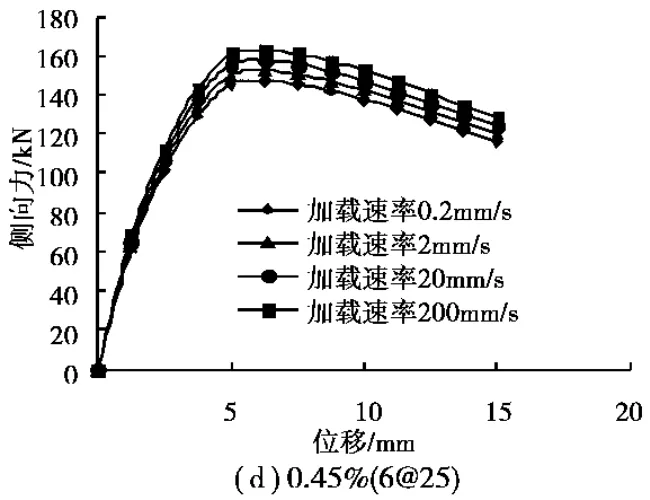
图8 不同体积配箍率下的力与位移曲线

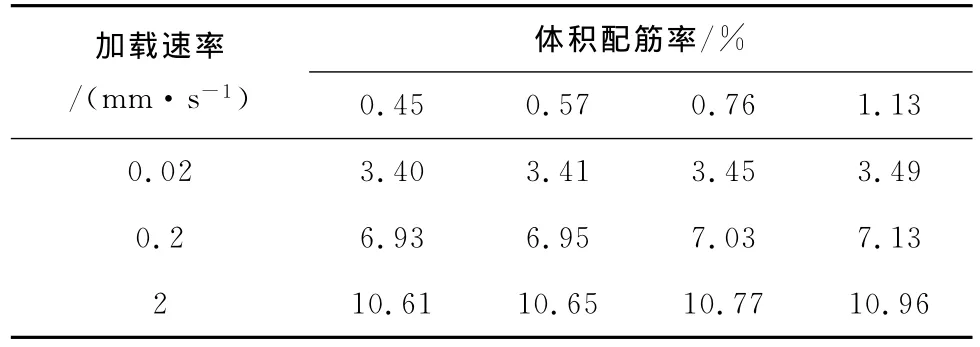
表3 钢筋混凝土柱在不同纵向配筋率下动力承载力增长率

3 结 语

我国现行的抗震设计规范并没有充分考虑应变率对材料本构关系以及结构构件的承载能力、变形、耗能能力和破坏模式的影响。考虑应变率对材料本构关系的影响，发展一种便捷且较为精细化的适用于动力荷载下钢筋混凝土柱力学性能分析的方法具有重要意义。

对具有不同配箍率和配筋率的钢筋混凝土柱在不同的加载速率下进行试验结果表明加载速率对钢筋混凝土柱的承载力有较明显影响。

基于考虑混凝土应变率效应的动力纤维单元模型，对快速加载试验中4个钢筋混凝土柱构件在不同加载速度下的动力性能进行的数值模拟结果与试验结果比较发现，在笔者试验所对应加载速率和应变率水平下，模拟结果与试验结果吻合较好，能较好反映试件的承载力及延性等特性。

采用经过试验验证的考虑应变率效应的纤维单元模型，对钢筋混凝土柱在不同纵向配筋率和体积配箍率下的动力性能进行的数值模拟结果表明不同纵向配筋率和体积配箍率的钢筋混凝土柱的承载能力随着加载速率的增加都有不同程度的增加，但纵向配筋率和体积配箍率对动力特性的影响呈现出不同的特征。高纵向配筋率试件的动力最大承载力相对增长率比低配筋率试件的要小，而高体积配箍率试件的动力最大承载力相对增长率比低体积配箍率试件的要大。

[1]ABRAMS DA.Effect of the rate of application of load on the compressive strength of concrete[J].ASTM J，1917，17：364-377.

[2]BISCOFF PH，PERRY SH.Compression behavior of concrete at high strain rates[J].Material and Structures，1991，144（24）：425-450.

[3]MALVAR LJ，ROSS CA.Review of strain rate effects for concrete[J].ACI Materials Journal，1998，95（6）：735-739.

[4]COTSOVOS DM，PAVLOVIC MN.Numerical investigation of concrete subjected to compressive impact loading.Part 1：A fundamental explanation for the apparent strength gain at high loading rates[J].Computes ＆Structures，2008，86（1／2）：145-163.

[5]COTSOVOS DM，PAVLOVIC MN.Numerical investigation of concrete subjected to compressive impact loading.Part 2：Parametric investigation of factors affecting behaviour at high loading rates[J].Computes ＆ Structures，2008，86（1／2）：144-180.

[6]COTSOVOS DM，PAVLOVIC MN.Numerical investigation of concrete subjected to high rates of uniaxial tensile loading[J].International Journal of Impact Engineering，2008，35（5）：319-335.

[7]OTANI S，KANEKO T，SHIOHARA H.Strain rate effect on performance of reinforced concrete members[J].Proceedings of fib symposium，Concrete Structures in Seismic Regions，Athens，May 2003.

[8]TAGAMI J，SUZUKI N，KANEKO T，et al.Dynamic loading test of reinforced concrete columns for identification of strain rate effect[C]／／Proceedings of the First NEES／E-Defense Workshop on Collapse Simulation of Reinforced Concrete Building Structures.Berkeley，California，2005：291-304.

[9]COTSOVOS DM，STATHOPOULOS ND，ZERIS CA.Behabvior of RC beams subjected to high rates of concentrated loading.Journal of Structural Engineering Structures，ASCE，2008，12：1839-1851.

[10]林旭川，潘鹏，叶列平，等.汶川地震中典型RC框架结构的震害仿真与分析[J].土木工程学报，2009，42（5）：13-20.LIN XU-CHUAN，PAN PENG，YE LIE-PING，et al.Analysis on damage mechanism of a typical RC frame in Wenchun earthquake[J].China Civil Engineering Journal，2009，42（5）：13-20.

[11]许斌，龙业平.基于纤维模型的钢筋混凝土柱应变率效应研究[J].工程力学，2011，28（7）：103-109.

[12]过镇海，时旭东.钢筋混凝土原理和分析[M].北京：清华大学出版社，2003.

[13]XIAO JZ，ZHANG CH.Seismic behavior of RC columns with circular，square and diamond sections [J].Construction and Building Materials，2008，22：801-810.

[14]PARK R.，PRIESTLEY MJN，GILL WD.Ductility of square confined concrete column [J].J Struct Eng ASCE，1982，108（4）：929-951.

[15]ComitéEuro-International du Béton.CEB-FIP Model Code 1990[M].London：Thomas Telford，1993.

[16]朱伯龙，董振祥.钢筋混凝土非线性分析[M].上海：同济大学出版社，1985.

[17]FU HC，ERKI MA，SECKIN M.Review of effect of loading rate on concrete in compression[J].J Struct Eng ASCE，1991，117（12）：3645-3659.