行波激励下圆柱面巨型网格结构的地震响应分析

贺拥军，李练兵，2，周绪红，3

（1.湖南大学 土木工程学院，长沙 410082；2.中机国际工程设计研究院有限责任公司，长沙 410007；3.兰州大学 土木工程与力学学院，兰州 730000）

随着科学技术的不断发展，空间结构越来越多地应用于工程实践。地震作用时，传统的较小跨度的空间结构一般很少考虑结构的空间变异性，结构各支承点处的地震动输入情况相同，但对于大跨度空间结构来说，空间变异性的影响可能比较突出，各支承点地震动不同，需要考虑由行波效应、频散效应以及局部场地效应等引起的多点激励影响[1－3]。近年来，国内外学者对多点激励下空间结构的地震反应进行了深入研究。黄明开和楼梦麟[4]采用时程方法对浦东机场候机楼进行了竖向地震行波效应分析；汪洋等[5]对两点支承平面结构进行了多点激励下的随机地震响应分析；苏亮等[6]提出了一种在空间地面运动下的平均反应谱方法。以上研究均表明，对大跨空间结构进行多点激励下地震响应分析是十分必要的。

巨型网格结构是一种可向超大跨度方向发展的新兴结构，其受力合理，结构主次分明，可跨越200m以上的空间（图2）。文献[7-9]曾分别对不同形式的巨型网格结构进行了深入的研究，但还未曾对结构的大跨度特征进行过行波激励下的地震响应分析。本文以80m跨的平板网架子结构圆柱面巨型网格结构为对象，假定不考虑频散效应及局部场地效应，重点分析其在行波激励下弹塑性性能及不同跨度下的行波效应，并与一致激励进行对比分析。

1 多点激励动力时程分析实现方法

目前，确定性动力时程分析法、随机振动分析法和工程反映谱法是研究结构多点激励下反应的3种分析方法[10－12]。其中确定性动力分析法假设地基条件一致，地震波沿地表以一定的速度传播，结构各支点接受到的地震波波形和大小一定，只是存在时间滞后现象。虽然时程分析方法没有考虑局部场地效应和频散效应，但也在一定程度上客观地反映了地震波在大跨空间结构中传播的基本反应特性[13－14]。支座大质量法是多点激励时程分析方法中较为常用的方法，即在结构支承处添加大质量块，通过在大质量块上施加地震加速度，以大质量块来带动上部结构的运动。如图1所示，设结构内部节点1和2为支座节点，分别与地基相连，地震时各支座节点与地面一起运动。由于地基质量难于确定，现将节点1、2与地基质量分别统一假设为质量M0，节点1和节点2处作用的加速度分别用ü1和ü2表示。则体系动力平衡方程可表示为：

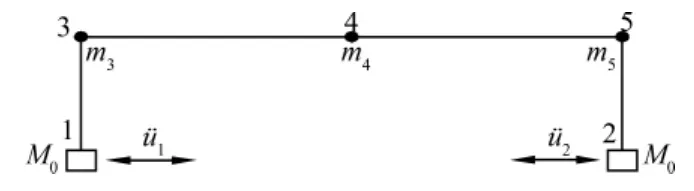
图1 支座大质量法模型

也就是说如果在支座节点处附加大质量块，就能使不同支承节点处施加不同的加速度，即实现多点激励。本文将大质量方法引入大型通用有限元软件ANSYS中，采用Newmark-β法进行动力时程分析。

2 纵波输入下行波激励地震响应分析

2.1 结构模型及地震输入

取平板网架子结构圆柱面交叉立体桁架系巨型网格结构的跨度为80m，矢跨比0.2，立体桁架梁高度3.6m，结构大网格数为4×4，立体桁架梁段内网格数为6，主结构杆件截面规格φ140×4.5；子结构采用双层平板网架，网格数9×9，杆件截面规格为φ76×4.0，子结构周边铰接。结构上表面承受1kN／m2的竖向均布荷载，通过自编程序将其转化为上弦节点集中质量处理，主体结构采用两纵边上下弦固定铰支。结构有限元模型如图2所示（为了清楚可见，子结构仅部分画出），杆件采用Q235钢，钢材密度7800kg／m3，弹性模量216GPa，泊松比为0.3，在通用有限元分析软件ANSYS中，模型杆件采用Link8单元，杆件之间均为铰接连接，上弦节点集中质量用Mass21单元。分析时采用适于二类场地的EL-Centro水平地震分量对结构在8度罕遇地震作用下进行一致地震激励和仅考虑行波效应的多点激励，地震传播方向为X向，地震作用方向为Y向（如图2），根据《建筑抗震设计规范（GB 50011—2010）》，将地震记录水平加速度峰值修正为400cm／s2，计算时间步长0.02s，地震持时15s。考虑到计算分析耗时问题，仅对主体结构单独承载情况进行分析，考虑行波效应时分别取视波速为100、200、400、600、1000m／s进行分析。

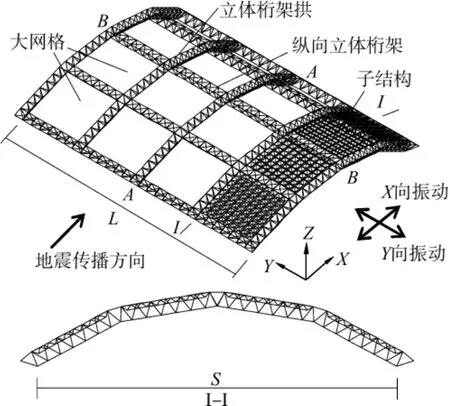
图2 平板网架子结构圆桩面巨型网格结构

2.2 不同视波速下弹塑性位移

表1反映了考虑弹塑性时结构在一致输入和多点输入下位移峰值情况。从表中可以看出，一致输入和多点输入下，三向位移中Z向位移峰值最大，Y向位移峰值最小，X向位移峰值随视波速的减小而递增，当视波速为100m／s时，X向位移峰值为一致输入下的3.182倍；Y向位移峰值和Z向位移峰值随视波速的减小先增大后减小，当视波速为200m／s时，Y向位移峰值和Z向位移峰值最大，分别为一致输入下的2.724和2.622倍。

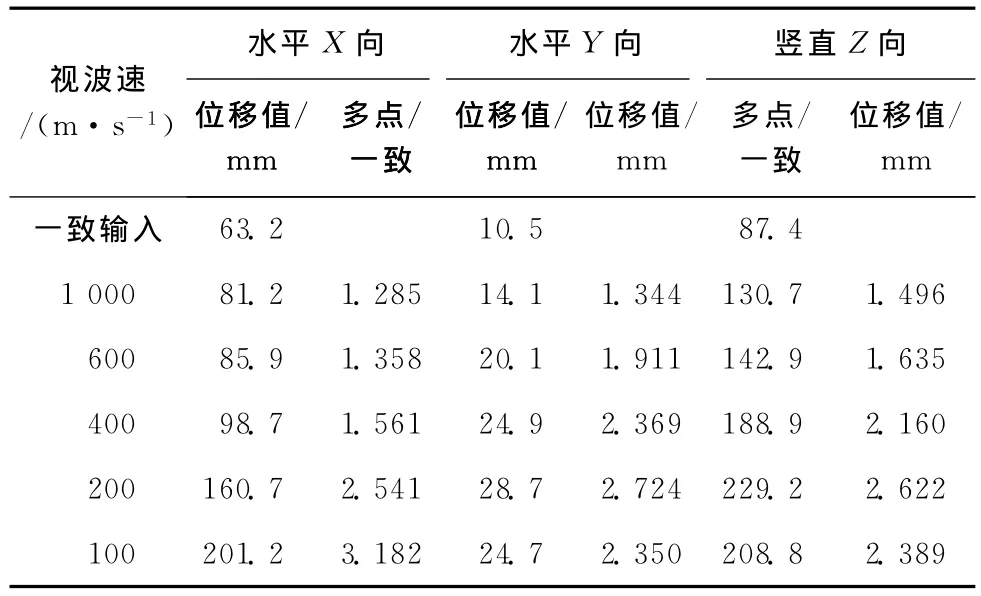
表1 位移峰值

2.3 不同视波速下弹塑性应力

表2反映了一致输入和多点输入下各应力范围内的杆件根数变化情况，统计结果表明：

1）无论是一致输入还是多点输入，大部分杆件应力集中在50MPa至100MPa之间，占总杆件数的50%以上，应力大小在100MPa以下的杆件占绝大多数，占到80%以上。

2）将190MPa定义为危险应力，则由表可以看出，随着视波速的减小，危险杆件数量不断增多，在视波速为200m／s时，危险杆件数量为183根，占到总杆件数量的7.67%。

3）在视波速大于100m／s情况下，进入屈服的杆件数随视波速的减小而不断增加，200m／s时达到111根，说明结构在行波效应下进入塑性的杆件数目增多。

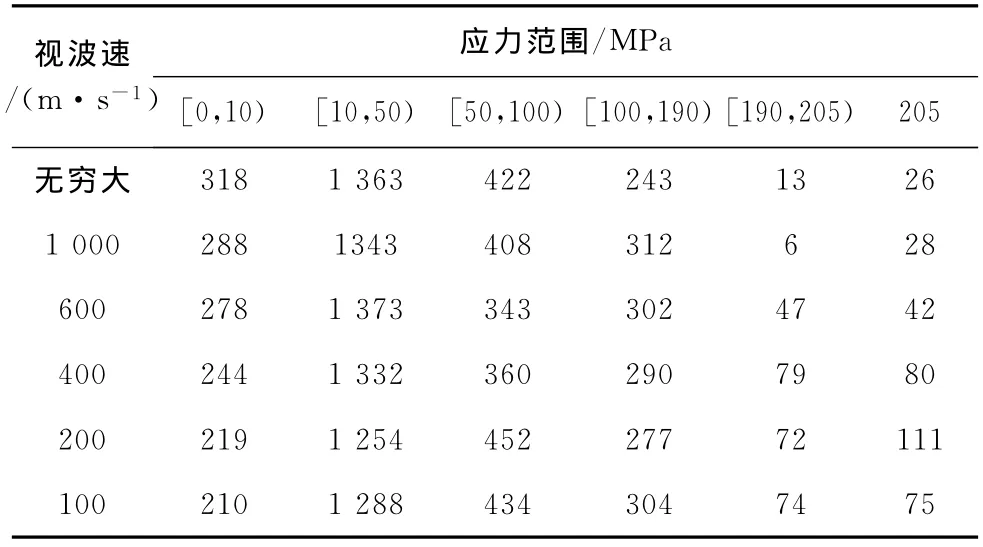
表2 应力范围内杆件根数

2.4 屈服杆件数量随时间变化

分析表明，随着地震加速度的强弱变化，杆件应力在弹性和弹塑性之间往复变化，不同视波速下结构屈服杆件数量随时间的变化情况如图3所示，从图中可以看出，一致输入下首批屈服杆件出现的时刻较地震加速度峰值时刻有少许滞后（前者在2.24s，后者在2.12s），而行波效应下首批屈服杆件出现的时刻均较地震加速度峰值时刻要早，且随视波速的不断减小而不断提前，视波速为100m／s时，首批屈服杆件在1.74s时便出现。随着视波速的减小，地震作用时间范围内屈服杆件出现的频次不断增加，在图中表现为分布图逐渐饱满。视波速为200m／s时，同一时刻进入塑性的最大杆件量为35根。从图中还可以发现，行波效应对屈服杆件的影响不仅表现在屈服杆件数量的大小上，而且表现在屈服杆件在地震作用时间范围内的广度上。

2.5 杆件应力影响率分析

图4反映的是不同视波速下杆件应力与一致地震输入下对应杆件应力之比影响率的分布图，从分布图看出，影响率绝大部分都小于5，大于5的仅占小部分，行波效应使部分杆件应力减小，部分杆件应力增大。表3为不同视波速下杆件应力影响率大于1所占百分比统计，由结果来看，随着视波速的减小，影响率大于1的所占百分比不断提高，说明行波效应的“增力”作用随视波速的减小而突出。

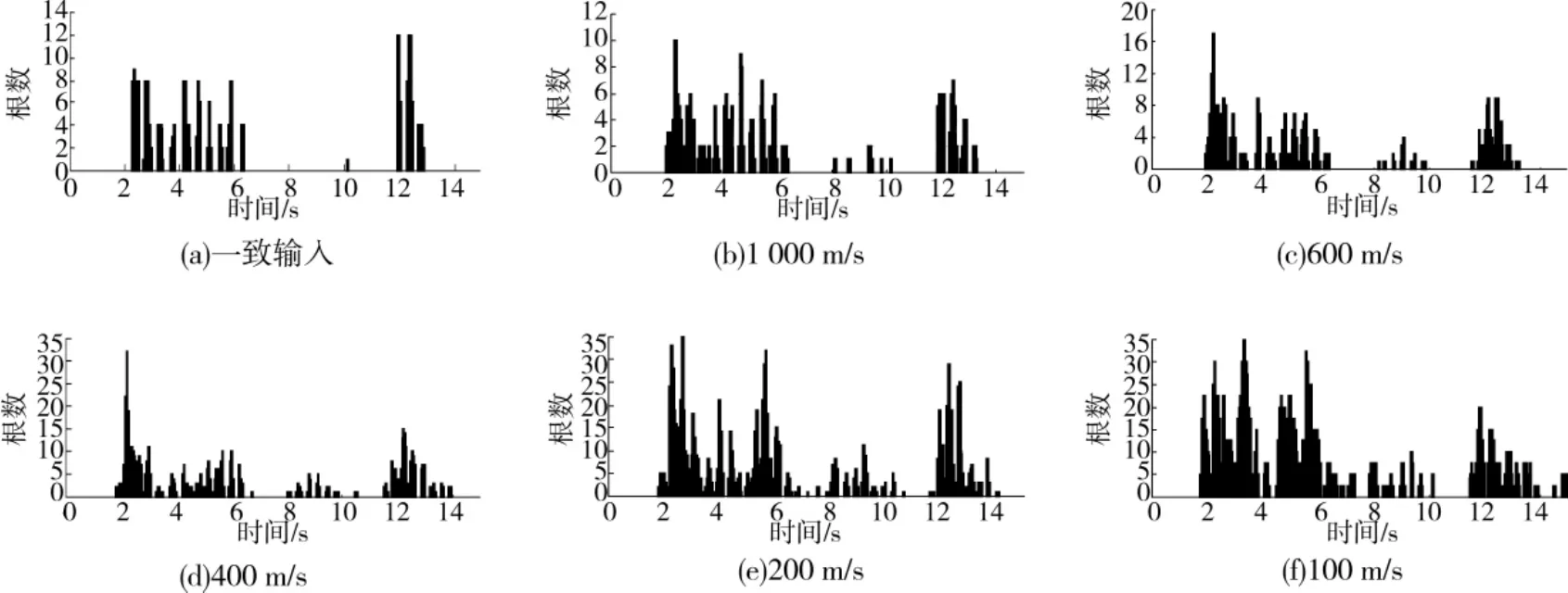
图3 不同视波速下屈服杆件数量随时间变化

图4 不同视波速下杆件应力影响率分布

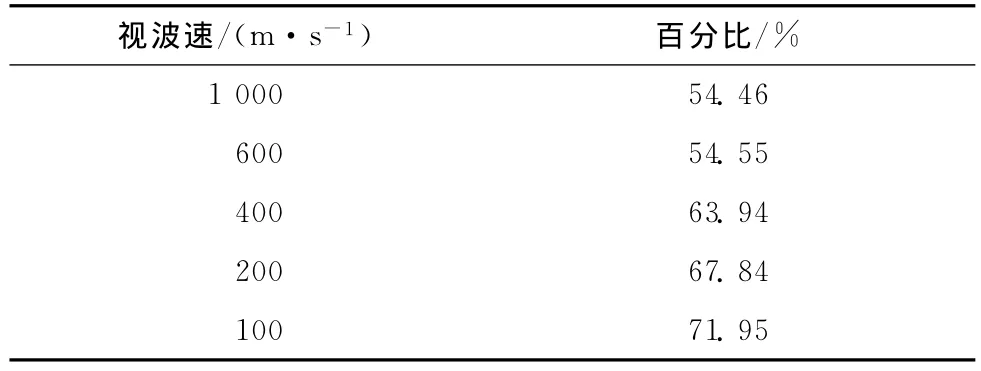
表3 不同视波速下杆件应力影响率大于1所占百分比

3 横波输入下行波激励地震响应分析

3.1 结构模型及地震输入

结构模型及地震波选用同2.1节，不同的是考虑横波输入，即地震传播方向沿X向，振动方向沿Y方向，如图2所示，考虑行波效应时分别取视波速为100、200、400、600和1000m／s。

3.2 不同视波速下弹塑性位移

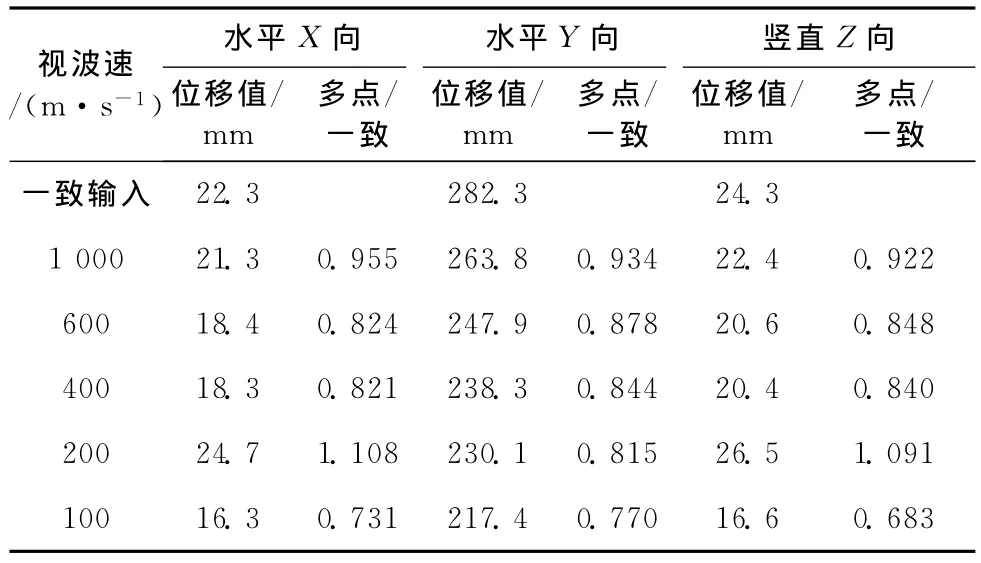
表4 位移峰值

表4反映了横波输入时结构在一致输入和多点输入下位移峰值情况。由表可知，一致输入和多点输入下，三向位移中Y向位移峰值最大，远大于另外两向位移，X向和Z向位移相当，Z向稍大，Y向位移峰值随视波速的减小而减小；除200m／s外，其余视波速下Y向和Z向位移峰均较一致输入下要小。这是由于单独承载时结构纵向刚度较小所致，刚度越小，影响越小。

3.3 不同视波速下弹塑性应力

表5反映了一致输入和多点输入下各应力范围内的杆件根数变化情况，结果表明：

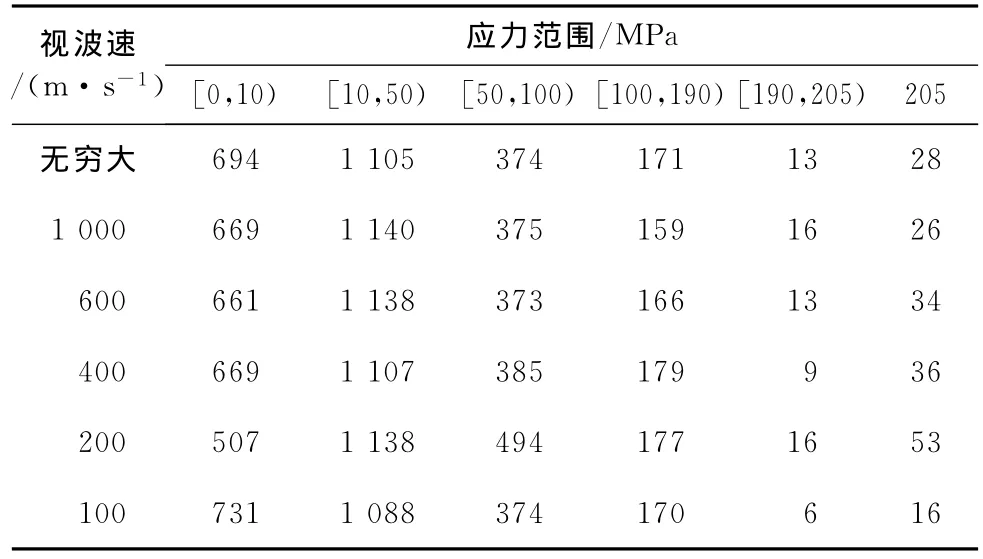
表5 应力范围内杆件根数

1）不同视波速下弹塑性应力分布情况基本与3.2节中的纵波输入相一致，应力大小在100MPa以下的杆件更多，占到89%以上。

2）视波速在200m／s以上时，屈服的杆件数随视波速的减小而不断增多，200m／s时达到53根，几乎达到一致输入下的2倍，而在视波速为100m／s时，屈服杆件数大幅减少，甚至少于一致输入下的数量。

可见横波输入时行波效应在一定范围内使进入塑性的杆件数目增多，但视波速特别小时，行波效应使屈服杆件数减少。

3.4 屈服杆件数量随时间变化

不同视波速下结构屈服杆件数量随时间的变化情况如图5所示，从图中可以看出，一致输入和多点输入下首批屈服杆件出现的时刻均较地震加速度峰值时刻要滞后（地震加速度峰值时刻在2.12s），视波速为100m／s时，首批屈服杆件在4.34s时才出现，远滞后于地震加速度峰值时刻。视波速较大（大于等于400m／s）时，地震作用时间范围内屈服杆件出现的频次相差不大，而视波速较小（100m／s）时，地震作用时间范围内屈服杆件出现的频次明显减小，同一时刻屈服杆件数目也明显小于其他视波下的数目，可见，横波输入时，较小视波速下行波效应对结构杆件应力的“减力”作用明显。

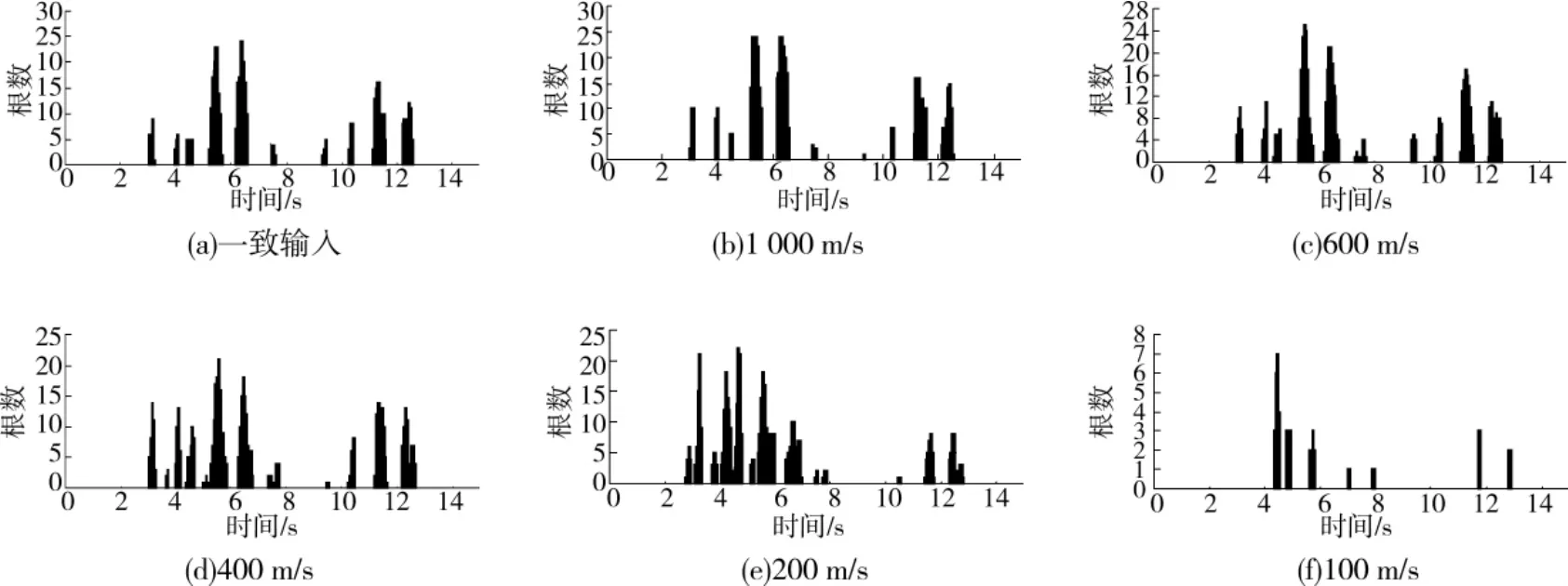
图5 不同视波速下屈服杆件数量随时间变化

3.5 杆件应力影响率分析

表6为不同视波速下杆件应力影响率大于1所占百分比统计，图6反映的是不同视波速下杆件应力与一致地震输入下对应杆件应力之比影响率的分布图，可以看出，应力影响大于1所占百分比随视波速的减小先增大后减小，视波速为1000m／s时，结构内部增力杆和减力杆相当，视波速为200m／s时，增力杆达到70.19%，而当视波速小到100m／s时，结构内部减力杆占主导，达到69.31%，进一步说明横波输入时，较小视波速下行波效应对结构杆件的“减力”作用十分明显。

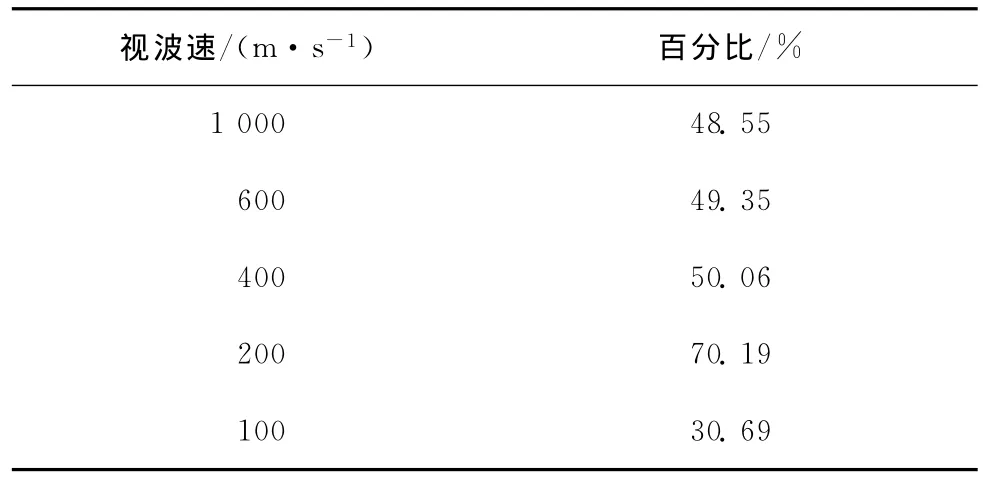
表6 不同视波速下杆件应力影响率大于1所占百分比

图6 不同视波速下杆件应力影响率分布

4 多维行波激励地震反应对比分析

地震波为震源辐射的弹性波，发震时以波的形式向四周传播，地震时需要考虑地震的3个分量作用，上述2节重点分析了水平横向和纵向地震振动下的结构反应，本节从多维多点的角度来对比分析圆柱面巨型网格结构的弹塑性性能，结构模型同2.1节，分别考虑水平X向，水平XY向以及XYZ三向地震作用下的行波激励响应，地震视波速以400m／s为代表，并与一致地震响应进行对比。

图7为不同激励作用下的三向弹塑性位移峰值情况，从图中可以看出：一致输入时，水平拱向位移在一维、二维和三维地震输入下依次有所递增，但相差不大，行波激励时，其值在水平二维地震输入下最大，且均大于一致输入下的值，说明行波激励时，竖向地震分量对拱向位移有“减小”作用；和一致输入类似，行波激励时，水平纵向位移在水平二维和三维地震输入下的值几乎相等，但行波激励下的值明显要小于一致输入下的值，而水平拱向地震输入下的值均很小，可见纵向位移主要由纵向地震分量引起，多维地震输入下的行波效应对纵向位移起“减小”作用；一致输入时，竖向位移的大小随地震输入的维数影响不大，而行波激励时，竖向位移在三维地震输入下明显增大，说明行波激励下竖向地震分量对竖向位移影响甚大。

图8表示的是不同激励作用下屈服杆件数量情况，由图可知：行波激励时，一维、二维、三维地震作用下的屈服杆件数均大于一致输入下的值，而不论一致输入还是行波激励，二维与三维地震作用下的屈服杆件数几乎相等，说明竖向地震分量对杆件应力影响不大，杆件应力大小主要由水平两向地震分量所决定。

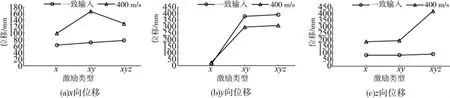
图7 不同激励下弹塑性位移峰值

图8 不同激励下屈服杆件数量

5 不同跨度下结构多点激励效应

以结构跨度为参数，研究不同跨度下圆柱面巨型网格结构的行波效应影响。分析时取60、80、100、120、150m5种不同跨度的结构为对象，统一取结构矢跨比为1／5，立体桁架梁高度因子为1.2，结构上表面均布荷载取1.0kN／m2，主体结构杆件截面规格为φ140×4.5。由上节可知，杆件应力的大小主要由水平两向地震分量所决定，本节以结构内力为控制指标，采用适于二类场地的EL-Centro二维水平地震分量对结构在8度常遇地震作用下进行一致地震激励和仅考虑行波效应的多点激励分析。

不同跨度下结构单独承载时随视波速变化的应力峰值情况如表7所示，从表可以看出，行波激励对不同跨度结构的敏感程度不同，当跨度大于等于80m时，与一致激励下的应力峰值相比，行波效应影响随视波速的减小呈先增加后减小的趋势变化，较小视波速下的应力峰值甚至小于一致激励下的应力峰值。不同跨度所对应的最敏感视波速不同，80m跨对应于400m／s，100m 跨对应于200m／s，120m跨对应于400m／s，150m 跨对应于400m／s，可见结构在多点激励下并非视波速越小，行波效应越明显，当视波速达到一定程度时，结构应力峰值有所降低，这可能是由于地震波相位差引起结构杆件正反应力部分抵消所致。结构跨度为60m时，不同视波速下的行波效应对结构内力峰值的影响很小，与一致激励的比值较为稳定，但比值已达到1.20倍左右，可见该结构在60m跨时也需要考虑多点激励的影响。

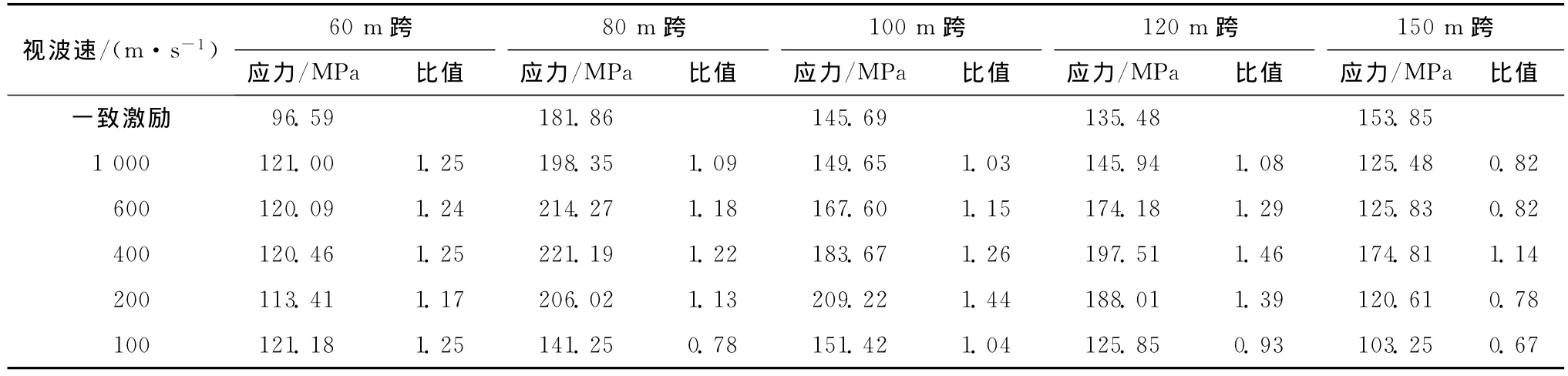
表7 不同跨度下的结构单独承载时随视波速变化的应力峰值

不同跨度下结构协同承载时随视波速变化的应力峰值情况如表8所示，从表可以看出，当跨度大于等于80m时，与一致激励下的应力峰值相比，和结构单独承载时不同，结构协同承载时行波效应影响随视波速的减小而增加，但跨度很大（如150m跨）时，在视波速小于等于400m／s情况下，各应力峰值变化已较小，行波效应的差别不明显，同时即便是视波速小到100m／s，行波效应对该跨度结构的应力峰值影响也只比一致激励提高44%，远小于其它跨度下的相应值。从表可见，视波速越小，结构协同承载下的行波效应对各跨度结构应力峰值越敏感，结构在60～120m跨时，100m／s视波速下的行波效应影响是一致激励下的3倍左右，影响较为显著。同时综合表7和表8来看，结构协同承载时的行波激励效应要大于结构单独承载下的效应，150m跨时，在视波速为100m／s的行波激励下，协同承载下的应力峰值达到单独承载下的2倍。

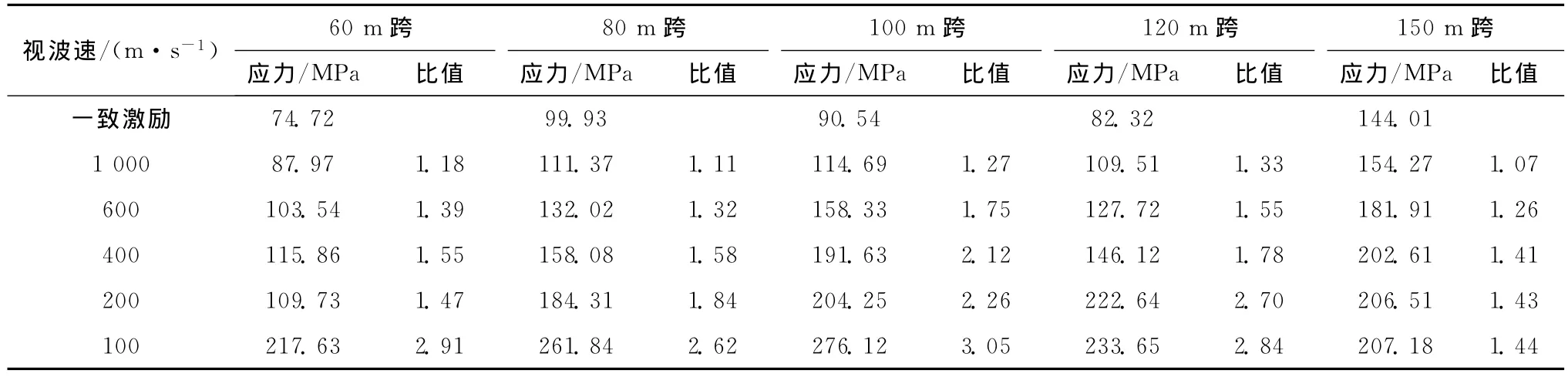
表8 不同跨度下的结构协同承载时随视波速变化的应力峰值

5 结 论

分析了圆柱面巨型网格结构在一维横向和多维罕遇地震作用下的弹塑性地震反应性能，以及不同跨度下结构的行波激励效应，得出以下结论：

1）纵波行波输入时，三向位移中竖向位移峰值最大；横波行波输入时，纵向位移峰值最大，其随视波速的减小而减小，这是由于单独承载时结构纵向刚度较小所致，且刚度越小，影响越小。

2）行波效应对屈服杆件的影响不仅表现在屈服杆件数量的大小上，而且表现在屈服杆件在地震作用时间范围内的广度上；但需要注意的是，横波行波输入时，100m／s视波速下行波效应对结构杆件应力的“减力”作用明显。纵波行波效应使首批屈服杆件出现的时刻较地震加速度峰值时刻不断提前，而横波行波效应却相反。

3）行波激励时，不同维数地震输入下的结构地震反应差异明显，竖向地震分量对杆件应力影响不大，杆件应力大小主要由水平两向地震分量所决定。

4）当结构跨度在60m以上时，需要考虑行波激励影响，不同跨度结构的最敏感视波速不同，协同承载下的行波激励效应要大于单独承载下的效应，150m跨时，在视波速为100m／s的行波激励下，前者的应力峰值达到后者的2倍。因此，在对圆柱面巨型网格结构进行行波激励下的地震分析时考虑结构协同承载将更为安全和合理。

[1]胡聿贤.地震工程学[M].北京：地震出版社，2006.

[2]周国良，鲍叶欣，李小军，等.结构动力分析中多点激励问题的研究综述 [J].世界地震工程，2009，25（4）：25-32.ZHOU GUO-LIANG，BAO YE-XIN，LI XIAO-JUN，et.al.Review on dynamic analyses of structures under multi-support excitation[J]. World Earthquake Engineering，2009，25（4）：25-32.

[3]何庆祥，沈祖炎.结构地震行波效应分析综述 [J].地震工程与工程振动，2009，29（1）：50-57.HE QING-XIANG，SHEN ZU-YAN.Review of structural seismic analysis of travelling wave effects[J].Journal of Earthquake Engineering and Engineering Vibration，2009，29（1）：50-57.

[4]黄明开，楼梦麟.浦东机场候机楼竖向地震行波效应时程分析 [J].地震工程与工程振动，2009，29（3）：15-21.HUANG MING-KAI，LOU MENG-LIN.Time history of response to effect of vertical seismic traveling wave at Pudong Airport Terminal（Ⅱ）in Shanghai[J].Journal of Earthquake Engineering and Engineering Vibration，2009，29（3）：15-21.

[5]汪洋，石永久，王元清.两点支承平面结构多点输入随机地震响应分析 [J].湖南大学学报：自然科学版，2010，37（10）：13-19.WANG-YANG，SHI YONG-JIU，WANG YUANQING.Analysis on random seismic response of two supporting plane structures under multi-support excitation[J].Journal of Hunan University：Natural Sciences，2010，37（10）：13-19.

[6]SU LIANG，DONG SHI-LIN，SHIRO KATO.A new average response spectrum method for linear response analysis of structures to spatial earthquake ground motions[J].Engineering Structures，2006，28（13）：1835-1842.

[7]贺拥军，周绪红，董石麟.膜型网壳巨型网格结构的整体与局部稳定性研究 [J].土木工程学报，2005，38（2）：13-21.HE YONG-JUN，ZHOU XU-HONG，DONG SHI-LIN.Research of overall and local stability of reticulated megastructure with single layer membranous latticed shell substructure[J].China Civil Engineering Journal，2005，38（2）：13-21.

[8]HE YONG-JUN，ZHOU XU-HONG.Static properties and stability of cylindrical ILTDBS reticulated megastructure with double-layer grid substructures[J].Journal of Constructional Steel Research，2007，12（63）：1580-1589.

[9]ZHOU XU-HONG， HE YONG-JUN， XU LEI.Formation and stability of a cylindrical ILTKBS reticulated mega-structure braced with single-layer latticed membranous shell structures[J].Thin-Walled Structures，2009，5（47）：537-546.

[10]苏亮，董石麟.水平行波效应下周边支承大跨度单层球面网壳的地震反应 [J].空间结构，2006，12（3）：24-30.SU LIANG，DONG SHI-LIN.Seismic response of a large span single layer reticular dome with surrounding columns considering horizontal wave passage effect[J].Spatial Structures，2006，12（3）：24-30.

[11]ALLAM SAID M，DATTAT K.Seismic response of a cable-stayed bridge deck under multi-component nonstationary random ground motion[J]. Earthquake Engineering and Structural Dynamics，2004，33（3）：375-393.

[12]YE JI-HONG，ZHANG ZHI-QIANG，CHU YE.Strength failure of spatial reticulated structures under multi-support excitation [J].Earthquake Engineering and Engineering Vibration.2011，10（1），21-36.

[13]陈幼平，周宏业.斜拉桥地震反应的行波效应 [J].土木工程学报，1996，29（6）：61-68.CHEN YOU-PING， ZHOU HONG-YE. Seismic behavior of cable-stayed bridges under traveling wave excitation[J].China Civil Engineering Journal，1996，29（6）：61-68.

[14]HAO H，DUAN X N.Multiple excitation effects on response of symmetric buildings[J]. Engineering Structures，1996，18（6）：723-740.