混凝土浇筑仓温度双控指标拟定的最大熵法

黄耀英，瞿立新，周宜红，宫经伟，周绍武，李金河，陈文夫

(1.三峡大学水利与环境学院，湖北 宜昌 443002;2.武汉大学 水利水电学院，武汉 430072;3.中国长江三峡集团公司，湖北宜昌 443002)

1 研究背景

温度监控指标是混凝土大坝温控防裂的重要指标［1］。为了达到温控防裂的目的，需要控制浇筑仓最高温度和降温速率等。采用温度双控指标来动态控制混凝土浇筑仓最高温度无疑是一条新途径，即选取混凝土浇筑仓达到最高温度前典型龄期，拟定该龄期对应的容许温度和容许温度变化率，当该龄期下的混凝土温度和温度变化率超过容许温度和容许温度变化率时，预示着在当前温控措施下，浇筑仓混凝土温度极可能超过容许最高温度，必须采取更为有效的温控措施才能避免浇筑仓混凝土温度超过容许最高温度。

近年来，最大熵理论在结构可靠性分析［2］、岩土工程反分析［3］、岩石力学参数概率分布［4］、大坝安全监控指标的拟定［5］以及岩体结构加速流变破坏分析［6］等许多方面的应用取得了较好的效果。最大熵法不需要事先假设分布类型，直接根据各基本随机变量的数字特征值进行计算，这样就可以得到精度较高的概率分布密度函数［7］，进而求出混凝土浇筑仓温度双控指标。为此，本文结合西南某建设中的混凝土特高拱坝高温季节浇筑的混凝土浇筑仓实测温度，采用最大熵法拟定典型混凝土龄期的容许温度和容许温度变化率，以指导现场混凝土浇筑。

2 基本原理

2.1 信息熵的定义

1948年Shannon在创立信息论时，引入了信息熵的概念来研究信息的不确定性，即

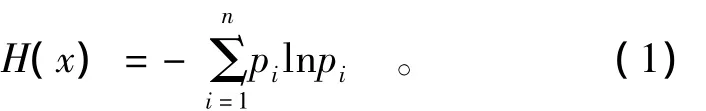
式中:pi是信息源中信号xi出现的概率;ln pi是它带来的信息量;H(x)表示信息量的大小，它是一个系统状态不确定的量度。

对于连续型随机变量，信息熵定义为

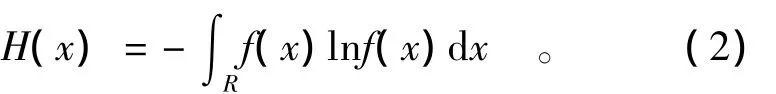
式中:f(x)是连续型随机变量x的概率分布密度函数。

2.2 最大熵密度函数［4-5］

由最大熵原理可知，最小偏差的概率分布是使熵H(x)在根据已知样本信息而施加的一些约束条件下达到最大值的分布，即

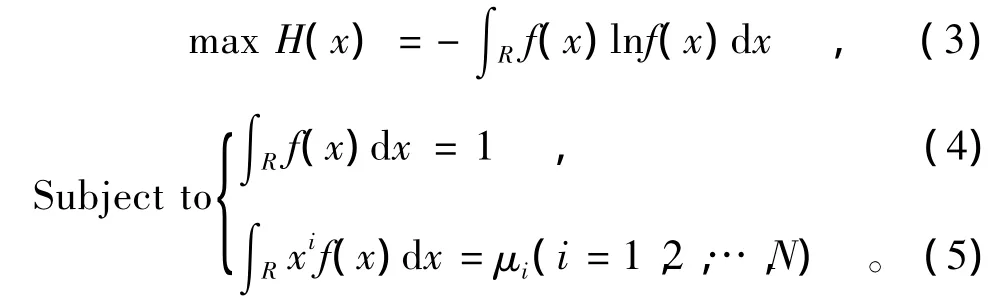
式中:R 为积分空间;μi(i=1，2，…，N)为第 i阶原点矩第j个样本值;n为样本数;N为所用矩的阶数。事实上，随机变量的特性基本上可以用它的前4阶矩来描述［4］;1阶矩即平均值刻画随机变量的取值“中心”;2阶矩或方差刻画随机变量围绕均值的离散程度;3阶矩(或偏度系数)刻画随机变量的对称性(偏倚程度);4阶矩(或峰度系数)刻画随机变量的集中和分散程度(尖平程度)。

可以调整f(x)来使熵H(x)达到最大值，具体可采用拉格朗日乘子法来分析这个问题。假设建立的拉格朗日函数为

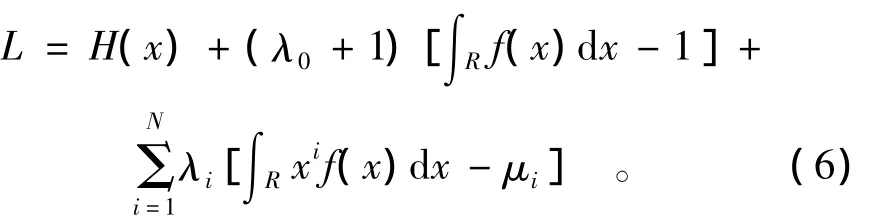
令∂L/∂f(x)=0，可得

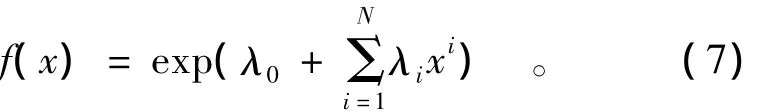
式(7)为最大熵概率密度函数的解析形式。

将式(7)代入式(4)，有

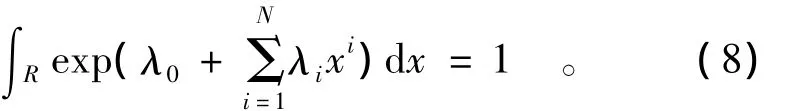
整理后可得

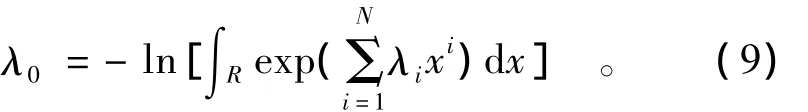
将式(7)和式(9)代入式(5)，有

吕温出使吐蕃途中写了《经河源汉村作》，诗中“伏腊华风亦暗存”指河湟地区已经几乎沦陷为吐蕃管辖，在吐蕃统治下的汉族遗民只能暗自保存民族风俗；“暂驻单车空下泪，有心无力复何言”是诗人停车后真实地看到眼前汉族遗民居住的村落、遗民的生活现状，作者无奈没有能力为同胞去改变现状，只能无助地流泪，无力地感叹。《蕃中答退浑词二首》中“万群铁马从奴虏，强弱由人莫叹时”[2]444也是吕温出使吐蕃途中所作，吐谷浑部落沦陷，汉族遗民成了“没蕃人”，看到昔日祖国的使者，“没蕃人”哭诉现状，表达对祖国的思念。吕温在出使吐蕃途中，用诗歌记录下这一时期流离失所的百姓——被历史遗忘的遗民们对故土的思念。

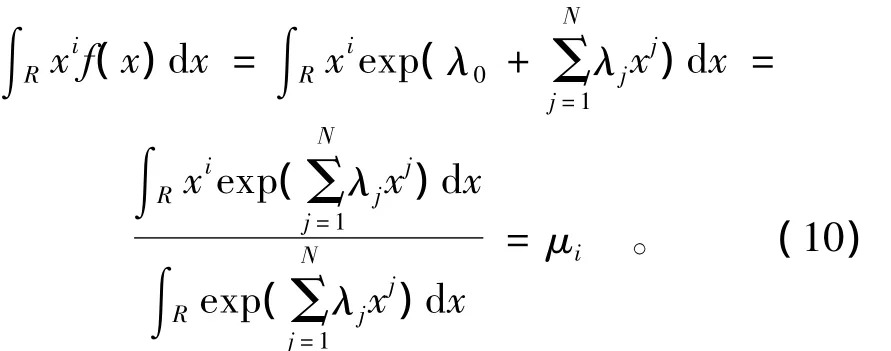
为便于求解拉格朗日乘子系数，将式(10)改为

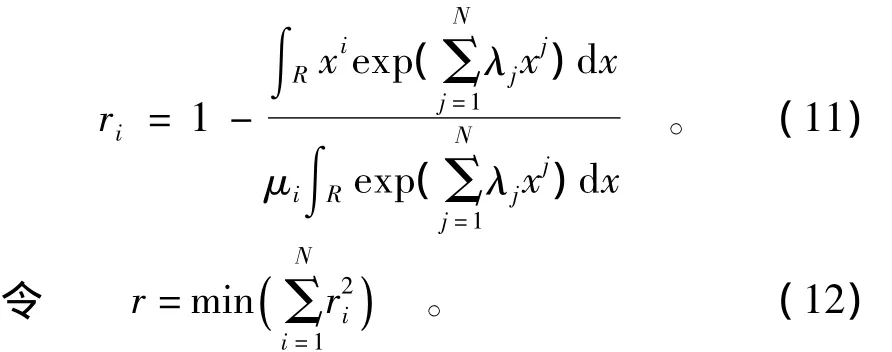
式中:ri为残差，可用优化算法来求式(12)表示的残差平方和的最小值。当r＜ε时，即认为该式收敛，从而解得(λ1，λ2，…，λN)。这里积分区域 R 可近似取［¯x－5σ，¯x+5σ］，¯x和σ分别为样本均值和标准差。

2.3 粒子群算法

为了获得高精度的最大熵概率密度函数，本文采用粒子群算法来优化求解拉格朗日乘子系数。粒子群算法(Particle Swarm Optimization，PSO)是Kennedy等在1995年提出的一种智能计算方法［8］。粒子群算法较其它进化算法具有简单易实现、参数少、较强的全局收敛能力和鲁棒性等优势［9］。标准PSO，粒子的速度和位置的更新公式为

式中:ω为惯性权重;c1，c2为加速常数，通常取c1=c2=2;rand和Rand为2个(0，1)随机数;Pbest为局部最好位置;Gbest为全局最好位置。

2.4 温度双控指标的拟定

由上述方法确定出随机变量x的最大熵概率密度函数f(x)。令xm为监测效应量的容许值，当x＞xm时，混凝土浇筑仓将出现超过容许最高温度，其概率为

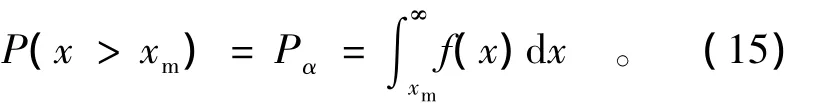
求出x的最大熵概率密度函数f(x)后，估计xm的主要问题是确定失效概率Pα，其值根据大坝重要性来确定，对于西南某特高拱坝，浇筑仓温度超过容许最高温度的概率较小，取α=5%，此时

分别获得混凝土浇筑仓达到最高温度前的典型龄期对应的温度和温度变化率样本，然后由式(7)求出最大熵密度函数f(x)，最后采用式(16)计算典型龄期对应的容许温度和容许温度变化率。

3 实例分析

3.1 粒子群算法的拉格朗日乘子系数优化

为验证粒子群算法寻优的准确度及效率，随机生成1 000 个标准正态分布样本，μ1=－0.004 35，μ2=0.995 5，μ3=－0.021 78，μ4=2.839 443，对应其最大熵密度函数为:f(x)=exp(－0.935 89+0.001 147x－0.462 77x2－0.001 93x3－0.006 93x4)，采用迭代步来确定收敛，在迭代200次时即出现最优值，对应残差平方和r＜10－32，其计算迭代过程及标准正态分布函数和计算的最大熵概率密度函数对比如图1，由此可见粒子群算法能较好地对拉格朗日乘子系数寻优。

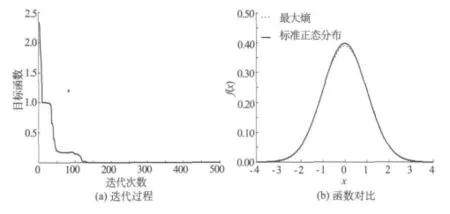
图1 迭代过程与结果对比图Fig.1 Iteration process and results

3.2 工程实例

西南某建设中的特高拱坝位于四川省雷波县和云南省永善县接壤的金沙江峡谷段，拦河大坝为混凝土双曲拱坝，坝顶高程610m，最大坝高285.5m，大坝共31个坝段，为达到温控防裂的目的，在混凝土浇筑仓埋设常规温度计，并且在典型坝段埋设分布式光纤进行温度监测工作。由于该拱坝规模巨大，混凝土材料抗裂性能一般，从提高施工期混凝土抗裂安全性出发，混凝土最高温度统一按27℃进行控制。

本文统计了该拱坝5#—25#坝段在高温季节浇筑(5—9月份)的97仓混凝土实测温度过程线，统计分析表明实测最高温度一般在混凝土龄期的5.6 d时达到。由此选取混凝土龄期为2.5 d和3 d时的温度和温度变化率作为样本进行分析，温度样本以及温度变化率样本的均值和标准差见表1。

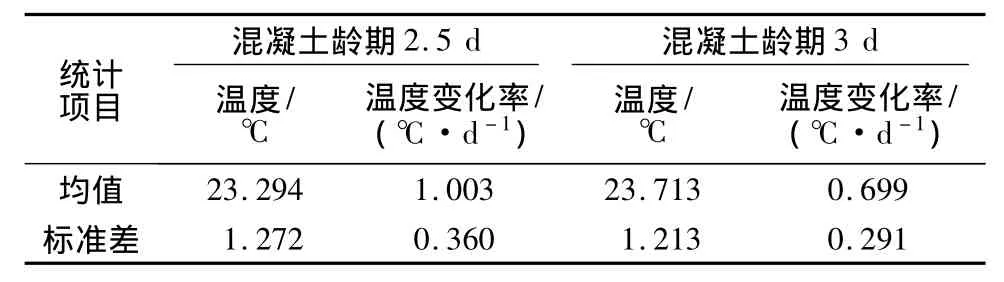
表1 统计样本均值和标准差Table 1 Average values and standard deviations of statistical samples

在计算混凝土龄期为2.5 d和3 d时的温度和温度变化率对应的最大熵概率密度函数时，为防止粒子群算法在寻优过程中陷入局部最优解，令ω=中maxstep为最大迭代步取1 000，k为当前迭代次数;c1=c2=2;粒子数N取30;由于随机变量的特性基本上可以用它的前4阶矩来描述，所以仅计算(λ1，λ2，λ3，λ4)，即空间 D 为4 维。为提高计算收敛速度和精度［10］，在计算温度样本对应的最大熵概率密度函数时，将式(7)略作转化为，μ1和 σ 分别为均值和标准差。各阶原点矩及拉格朗日乘子系数见表2，温度及变化率对应密度函数见图2。

表2 样本原点矩及优化的拉格朗日系数Table 2 Origin moments of samples and optimized Lagrange parameters

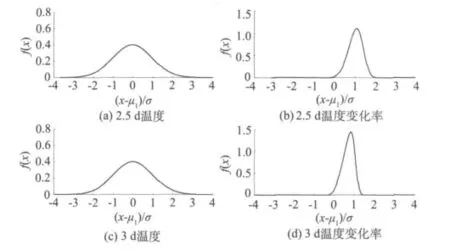
图2 概率密度函数Fig.2 Probability density functions

假设超温概率α=5%时，采用式(16)计算获得混凝土龄期为2.5 d和3 d时的容许温度和容许温度变化率，见表3。

表3 典型龄期下容许温度和容许温度变化率Table 3 Allowable temperatures and temperature rates at typical concrete ages

新浇筑混凝土因水泥水化热，温度逐渐升高，经过若干天后达到最高温度，然后降温。与之相对，温度变化率在初期大，后期逐渐减小，达到最高温度后开始降温，温度变化率由正值转为负值。显然，如果浇筑仓混凝土最高温度超过容许最高温度，那么在混凝土龄期为第n天(n=2.5 d或n=3 d)时，混凝土的温度和温度变化率一般应超过某个容许值。因此，基于上述拟定的混凝土典型龄期的温度双控指标，采用下述方式对高温季节浇筑的混凝土浇筑仓温度进行预警:，重点关注并采取更有效的温控措施;，关注并采取更有效的温控措施;，温度跟踪监测;，正常，按现有的温控措施执行。

式中:Tn和(∂T/∂t)n分别是混凝土龄期为n天(n=2.5 d或 n=3 d)时的温度及温度变化率;［Tn］和［(∂T/∂t)n］分别是混凝土龄期为n天时，拟定的容许温度和容许温度变化率。

4 结语

本文将最大熵法应用于混凝土浇筑仓温度双控指标的拟定，得到如下结论:

(1)结合西南某建设中的混凝土特高拱坝高温季节浇筑仓实测温度，采用最大熵法拟定了混凝土浇筑仓温度双控指标，即混凝土浇筑仓达到最高温度前典型龄期对应的容许温度和容许温度变化率。最大熵法不需要事先假设样本分布类型，直接根据各基本随机变量的数字特征值进行计算，就可以得到精度较高的概率分布密度函数，由此求出的温度双控指标是可行的。

(2)为了获得高精度的最大熵概率密度函数，采用粒子群算法来优化求解拉格朗日乘子系数，工程实例分析表明，采用粒子群算法来优化求解拉格朗日乘子系数具有简单易实现、参数少的优势。

［1］朱伯芳，张超然.高拱坝结构安全关键技术研究［M］.北京:中国水利水电出版社，2010.(ZHU Bo-fang，ZHANG Chao-ran.Researches on the Structural Safety of High Concrete Arch Dams［M］.Beijing:China Water Power Press，2010.(in Chinese))

［2］章 光，朱维申，白世伟.计算近似失效概率的最大熵密度函数法［J］.岩石力学与工程学报，1995，14(2):119－129.(ZHANG Guang，ZHU Wei-shen，BAI Shi-wei.A Method of Maximum Entropy Density Function for Calculation of Approximate Failure Probability［J］.Chinese Journal of Rock Mechanics and Engineering，1995，14(2):119－129.(in Chinese))

［3］陈 斌，刘 宁，卓家寿.岩土工程反分析的最大熵原理［J］.河海大学学报(自然科学版)，2002，30(6):52－55.(CHEN Bin，LIU Ning，ZHUO Jia-shou.Principle of Maximum Entropy for Back Analysis in Geotechnical Engineering［J］.Journal of Hohai University(Natural Sciences)，2002，30(6):52－55.(in Chinese))

［4］邓 建，李夕兵，古德生.岩石力学参数概率分布的信息熵推断［J］.岩石力学与工程学报，2004，23(13):2177－2181.(DENG Jian，LI Xi-bing，GU De-sheng.Probability Distribution of Rock Mechanics Parameters by Using Maximum Entropy Method［J］.Chinese Journal of Rock Mechanics and Engineering，2004，23(13):2177－2181.(in Chinese))

［5］丛培江，顾冲时，谷艳昌.大坝安全监控指标拟定的最大熵法［J］.武汉大学学报(信息科学版)，2008，33(11):1126－1129.(CONG Pei-jiang，GU Chong-shi，GU Yan-chang.Maximum Entropy Method for Determining Dam Safety Monitoring Indices［J］.Geomatics and Information Science of Wuhan University，2008，33(11):1126－1129.(in Chinese))

［6］黄耀英，郑 宏，田 斌.信息熵理论在岩体结构加速流变破坏分析中的应用研究［J］.长江科学院院报，2011，28(8):50－54.(HUANG Yao-ying，ZHENG Hong，TIAN Bin.Application of Information Entropy Theory to the Failure Analysis of Accelerated Rheology of Rock Structure［J］.Journal of Yangtze River Scientific Research Institute，2011，28(8):50－54.(in Chinese))

［7］JAYNESE T.Information Theory and Statistical Mechanics［J］.The Physical Review，1957，106(4):620－630.

［8］曾建潮.微粒群算法［M］.北京:科学出版社，2004.(ZENG Jian-chao.Particle Swarm Optimization［M］.Beijing:Science Press，2004.(in Chinese))

［9］潘全科，王 凌，高 亮.离散微粒群优化算法的研究进展［J］.控制与决策，2009，24(10):1141－1149.(PAN Quan-ke，WANG Ling，GAO Liang.The State of Art of Discrete Particle Swarm Optimization Algorithms［J］.Control and Decision，2009，24(10):1141－1149.(in Chinese))

［10］韦 征，叶继红，沈世钊.最大熵可靠理论在工程中的应用［J］.振动与冲击，2007，26(6):146－148.(WEI Zheng，YE Ji-hong，SHEN Shi-zhao.Engineering Application of the Maximum Entropy Reliability Theory［J］.Journal of Vibration and Shock，2007，26(6):146－148.(in Chinese))