土体自稳坡角和土钉墙稳定机理分析

杨育文，肖建华

(武汉市测绘研究院，武汉 430022)

1 研究背景

在边坡和土钉墙稳定分析中，目前工程中采用最广泛的方法是极限平衡法。尽管计算机技术的飞速发展为这种方法的应用提供了有利条件，但是，我们必须看到的是，极限平衡分析中引入了大量的假设条件，而且某个特定的方法只能适用于特定的条件，计算过程较复杂。另外，我们观测到滑塌边坡或土钉墙多以几个大的块体形式发生滑动。由极限平衡法计算得到的结果大多是近似的。对一岩土性质较均一的边坡，若已知坡角、坡高和土体物理力学参数值，能否由简单的计算就可以评判边坡的稳定性?很多学者在这方面作了大量的工作。早在1866年，Culmann就推导出边坡临界高度的计算式［1］。徐世光等用工程地质类比法得到边坡稳定判别模型［2］。邓雄业等根据力的平衡关系确定了边坡极限高度与坡角之间的关系［3］。本文从一个新的角度，确定土体自稳临界坡角，由此提出边坡稳定性评判方法，利用得到的结果来分析土钉墙稳定机理中的关键技术问题。

2 土体自稳坡角和边坡稳定性

2.1 公式推导

下面推导中，引入5个假设条件:①岩土边坡和土钉墙稳定分析属平面应变问题;②坡高范围内是均质岩土或岩土层性质相近;③潜在滑动面近似为平面，坡底以下土层稳定;④不存在地下水或地下水水位在坡底以下;⑤地面无超载。

如图1所示，一高度为h、坡脚为β的岩土边坡，重度γ，抗剪强度指标c，φ。假设一平面滑动面AC与水平方向夹角是α，滑动面上速度向量v与AC的夹角等于土体内摩擦角φ。土体自重w由下式决定:

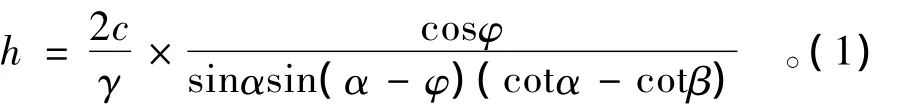
图1 岩土边坡滑动机理Fig.1 Translational failure mechanism of slope

当已知滑动面与水平方向夹角为α时，可用式(1)确定该边坡的极限自稳高度h。对式(1)中α求导，令其等于0，整理后得到

sin(β－ α)sin(2α－ φ)－sin(α－ φ)sinβ=0，求解得到α的临界值为

式(2)中αcr表示的是土体达到稳定极限平衡状态时潜在滑动面与水平方向的夹角。此时，可以证明AC面上剩余下滑力为零。当β=90°时，由式(2)得αcr=45°+φ/2，这与Rankine理论得到的结论一致。将式(2)代入式(1)中，得到边坡临界自稳高度为

式(3)与Culmann公式一致［1］。当β=90°时，由式(3)得

式(4)与垂直边坡推导出的结论一致［4］。

反过来，已知坡高h，由式(3)确定对应的自稳坡角为

式中:k1=4c cosφ +hγsinφ;k2=hγcosφ;k3=hγ。可以证明，式(5)中，当黏聚力c=0时，βcr=φ，土体临界自稳坡角与坡高h无关，由式(5)确定的βcr≥φ。对一均质岩土坡，在坡脚以下岩土能保持稳定的情况下，只要边坡坡角β小于或等于βcr，短期内可以自稳。

2.2 边坡稳定性评估

极限平衡法中，边坡稳定安全系数大多是指沿滑动破坏面的平均安全系数(lumped factor of safety)，从力或(和)力矩极限平衡条件中计算求解。稳定安全系数定义为沿滑动面土体可用的(available)抗剪强度τf与维持边坡极限平衡状态土体必须调动(mobilized)的抗剪强度 τm之比［5］，即

对无黏性土均质边坡(c=0)，当坡角β等于土体内摩擦角φ时，由式(6)的定义和土体单元力平衡条件，很容易就推导出边坡稳定安全系数FS=1.0。这时，由式(5)知 βcr=φ 。因此 βcr与β 之比也是1.0。

当土体黏聚力c≥0时，对一坡角为β的边坡(图(1))，其自稳临界坡角βcr由式(5)确定。在这里不以岩土的抗剪强度，而是以边坡相对坡角作为指标，将边坡稳定安全系数定义为

式(5)土体临界自稳坡角βcr计算式中，不仅包含了土体的抗剪强度参数c，φ，也包括了坡高或开挖深度h。因此，式(6)和式(7)这2种定义之间不存在矛盾。式(7)中的定义也表明:在相同土体抗剪强度条件下，坡高越高，边坡的稳定性就越低。从式(7)中可以看出，当FS=1.0时，边坡处于稳定极限平衡状态;当FS＞1.0时，边坡将处于稳定状态。安全系数越大，边坡稳定性越高。由表1中的标准作出判断。

表1 边坡稳定性评判标准Table 1 Slope stability evaluation standard

3 土钉墙稳定机理探讨

图2表示一土钉墙支护，β是基坑开挖坡角，临界角αcr，βcr分别由式(2)和式(5)确定。下面分析随着基坑开挖深度的增加，土体临界坡角的变化和土钉支护结构发挥的作用。

图2 土钉墙稳定机理分析Fig.2 Stability mechanism of soil nail wall

如图2(a)所示，当开挖深度h小于自稳临界值hcr时，坡角β＜βcr，土体可以依靠潜在滑动面AD上岩土自身产生的抗滑作用维持稳定，土体抗滑作用大于下滑作用，土钉等不发挥作用;随着开挖深度的增加，临界坡角βcr逐步变小，当开挖深度等于hcr时，坡角β=βcr，滑动面AD上抗滑作用等于下滑作用(图2(b))，土体ABD达到稳定极限状态，此时土钉等也不发挥作用;开挖深度继续增加，当h＞hcr，土体为了寻求自稳、建立新的平衡状态，临界坡角βcr将“自动地”进一步变小，自稳坡面AB绕A点发生顺时针转动，变成了AC(图2(c))，土钉墙主动区内出现了新自稳坡面AC。由于AC左侧坡面上存在土块ABC自重荷载，这时潜在滑动面AD上岩土本身的抗滑作用将无法维持自身稳定。此时土钉支护将发挥抗滑作用。

图2(c)中，由于ABC土体靠近临空面较近，应力释放程度较高，将出现沿着新的自稳坡面AC下滑的趋势，于是形成了土体I区。土体I区称为第一滑动区，它需要土钉等提供抗滑作用才能重新保持稳定。开挖深度越大，I区范围也越大。AC和AD之间是II区，它同样会发生向坑内的移动，是第二滑动区，其范围随开挖深度逐步变小。第一和第二滑动区都属于土钉墙主动区，余下的III区，是土钉墙的被动区。

图2(c)中，AC是由土体临界自稳坡角βcr确定的自稳坡面。当AC面上土体抗滑作用小于滑动作用时，将沿AC出现滑动面，称为第一滑动面。第一滑动面出现后，只是边坡局部失稳，所以也可称为局部滑动面。AD是土钉墙的主动区潜在滑动面，与Rankine主动滑动面类似，称为第二滑动面。当AD面上土体抗滑作用小于滑动作用时，土钉墙将整体失稳，所以也称整体滑动面。

土钉墙是柔性支护，刚度小，主动区土体可向坑内发生一定的移动，自我调节受力状态。图2(c)中，当AC和AD这2个滑动面充分发育延伸到地表时，地表将出现与基坑开挖边界近似平行的2条较大裂缝。这与我们在现场观测到的现象是相符的:一条离开挖边界较近，大约0.3～0.6倍的开挖深度，另外一条则较远，约1～1.5倍的开挖深度［6］。土钉墙能充分地发挥土体的自稳能力，是一种经济的支护方式。在类似的地质条件和相同的开挖深度情况下，土钉墙造价几乎只是桩棑支护的一半。

4 工程应用

4.1 实例 1［2］

云南元江—磨黑高速公路边坡，坡底稳定。公路在建设过程中高边坡多达432处，其中产生变形破坏的边坡达177处，原文选取28处滑塌边坡进行了统计分析。本文选择其中的前5处边坡的数据，利用本文推导出式(5)和稳定安全系数定义(式(7))进行了分析，结果如表2所示。

计算结果表明，表中边坡稳定安全系数变化范围为0.60～0.76之间，均小于1.0。根据表1 评定，这些边坡都处于不稳定状态。这一结论与工程实际情况是相符的。

4.2 实例 2［3］

雅安—泸沽高速公路文武坡喇嘛溪沟段路基边坡，该段路基开挖后，左侧边坡高达40余m，坡角45°，由昔格达组砂泥岩、局部夹砾岩透镜体构成，胶结程度差，工程性质与土相类似，坡底稳定。天然状态下岩土参数:重度18.5 kN/m3，剪切参数c=42.5kPa，φ=19°。该边坡是稳定的。

边坡坡高按40m计算，将相关参数代入式(5)，得到岩土自稳临界坡角 βcr=53.3°，大于边坡坡角45°。安全系数由式(7)确定，得到FS=1.19。由表1评判该边坡是稳定的。计算得到的结果与实际情况一致。

4.3 实例 3［5］

一饱和黏土基坑，开挖深度8 m，坡面与水平分向夹角45°，坑底以下土层稳定。黏土重度γ=19 kN/m3，不排水强度参数cu=65kPa，φu=0。

将相关参数代入式(5)，得到βcr=119.4°。由于饱和黏土cu较大，导致 βcr＞90°。由式(7)得到其稳定安全系数FS=2.65，大于1.2，由表1评判该边坡属于很稳定基坑。由力矩平衡条件得到的最小安全系数FS=2.37［5］。两者比较接近。

为了全面地验证本文提出的计算方法，以上选取了不稳定、稳定、很稳定3种不同类型的边坡。计算结果表明，本文提出的岩土边坡稳定计算方法和评判标准是合理的。

5 结论

表2 岩土边坡稳定性验算Table 2 Slope stability evaluation

在边坡坡底以下岩土层能保持稳定的前提条件下，边坡或土钉墙的稳定由坡底以上土层的力学性质和边坡几何尺寸决定。本文针对这种情况，提出了计算方法。该方法不需要大量的计算就很容易得到边坡稳定安全系数，可用于初步评估边坡稳定性。文中方法不能代替其它复杂方法。文中得到下面一些结论:

(1)本文首次由经典的上界定理推导出土体自稳临界坡角计算式，提出以相对坡角作为指标评判边坡稳定性的方法。以坡角和以土体的抗剪强度作为评定指标，它们不存在矛盾。前者的优点是方法简单，不需要大量的计算，可广泛应用于人工边坡(如放坡开挖基坑、填土边坡)、自然斜坡和滑坡的稳定性评估。

(2)在采用土钉墙支护的基坑工程中，当面层坡角小于土体自稳坡角时，土体可以自稳，土钉等支护结构不发挥作用。随着开挖深度的增加，当超过临界自稳深度或坡角大于土体自稳坡角时，土体中将出现由自稳坡角决定的第一滑动面。第二滑动面与Rankine主动滑动面类似，与土钉墙整体稳定相关。只有当土钉墙中出现第一滑动区时，土钉支护结构才发挥抗滑作用。

［1］蒋忠信.边坡临界高度卡尔曼公式之工程应用［J］.岩土工程技术，2007，21(5):217－220.(JIANG Zhongxin.Engineering Application of Culmann’s Formula on Critical Height of Slope［J］.Geotechnical Engineering Technique，2007，21(5):217－220.(in Chinese))

［2］徐世光，祝传兵，殷 瑛.一个极限稳定坡角与坡高的经验关系式［J］.中国地质灾害与防治学报，2006，17(3):22－26.(XU Shi-guang，ZHU Chuan-bing，YIN Ying.Empirical Correlation Between Limiting Slope Angle and Slope Height［J］.The Chinese Journal of Geological Hazard and Control，2006，17(3):22－26.(in Chinese))

［3］邓雄业，柴春阳，王小兵.土质边坡极限稳定坡角与极限高度分析［J］.路基工程，2008，(2):109－110.(DENG Xiong-ye，CAI Chun-yang，WANG Xiao-bing.Relationship Between Stability Angles and Limit Heights of Soil Slopes［J］.Subgrade Engineering，2008，(2):109－110.(in Chinese))

［4］CHEN WF.Limit Analysis and Soil Plasticity［M］.Amsterdam:Elsevier，1975.

［5］CRAIG R F.Soil Mechanics(The Sixth Edition)［M］.New York:Spon Press，2002.

［6］陈利洲.土钉墙的两条滑裂面成因分析［J］.工业建筑，2005，35(增刊):503－505.(CHEN Li-zhou.Analysis of Cause of Two Sliding Surface on Soil-Nailed Wall［J］.Industrial Construction，2005，35(Sup.):503－505.(in Chinese))