梯形明渠共轭水深计算方法

李 蕊，王正中，张宽地，王志刚

(1.杨凌职业技术学院公共课教学部，陕西杨凌 712100;2.西北农林科技大学水利与建筑工程学院，陕西杨凌 712100)

1 研究背景

在水工建筑物的下游消能计算中，常常遇到梯形明渠共轭水深的计算，其计算方程式是一个高次方程，没有直接的解析解。因此工程上常采用试算法或图解法来完成求解工作。试算法在计算上较为麻烦，在查曲线时也容易产生一定的误差，影响精度。图解法是利用已经制好的图表求解，计算比较快捷，但精度欠佳。为此，国内外学者对梯形明渠共轭水深的计算方法进行了多年研究，并取得了大量成果，但目前存在的主要问题仍然是计算精度不高，适用范围受限，或计算式过于复杂。

梯形明渠水跃共轭水深的计算在水工消能设计中具有重要的意义。本文通过对水跃方程进行数学变换，应用迭代理论及一元二、三次方程提出了梯形明渠共轭水深的直接计算公式。该公式使用方便简捷，且精度完全符合工程计算要求，从而克服了查图表法精度低、试算法盲目性大且繁琐等缺点。

2 梯形明渠共轭水深的基本方程

共轭水深是指:跃前水深h1和跃后水深h2。水流由急流过渡到缓流，会产生一种水面突然跃起的特殊的局部水力现象，称为水跃。如图1所示。

图1 水跃Fig.1 Hydraulic jump

梯形明渠水跃的基本方程为［1－2］

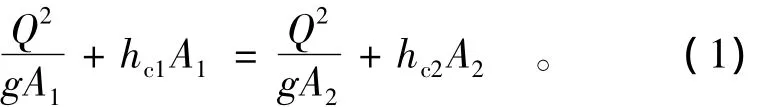
式中:Q为渠道的流量;A1，A2分别为水跃前、水跃后断面的过水断面面积;hc1，hc2分别为水跃前、水跃后断面形心距水面的距离;g为重力加速度。

当明渠断面的形状、尺寸以及渠中的流量一定时，水跃方程的左右两边都仅是水深的函数，即

因此，水跃方程也可以写成如下的形式，

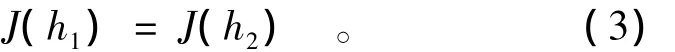
对于梯形断面各水力要素:

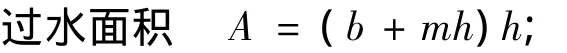
形心距水面的距离

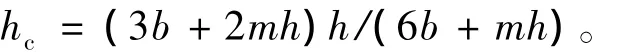
其中:b为梯形明渠断面底宽;h为梯形明渠水深;m为边坡系数。

将以上各式代入式(1)，得

其中:q为梯形明渠虚拟单宽流量;k为梯形明渠虚拟单宽流量时水流的动量。

3 水跃共轭水深的迭代公式

(1)跃前水深的迭代公式由(5)式可得

故跃前水深的迭代公式为

(2)跃后水深的迭代公式由(5)式可得

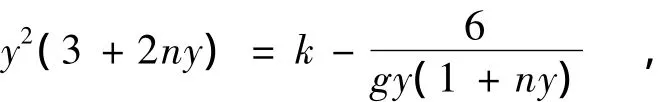
故跃后水深的迭代公式为

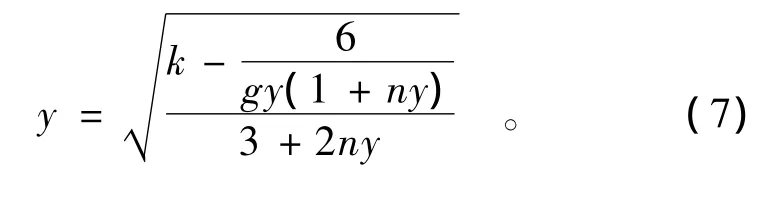
4 迭代公式收敛性分析

根据参考文献［4］第155页迭代法收敛定理知，若方程x=ø(x)的根为a，则迭代形式xk+1=ø(xk)收敛于a的条件是:①在a的某一邻域|x－a|＜δ内|ø'(x)|＜1;②当x∈［x1，x2］时，ø(x)∈［x1，x2］。则以该邻域内任意点为初值的迭代都是收敛于a的。因此，只要能证明以上迭代函数的导数的绝对值小于1，则可以证明该迭代函数是收敛的。

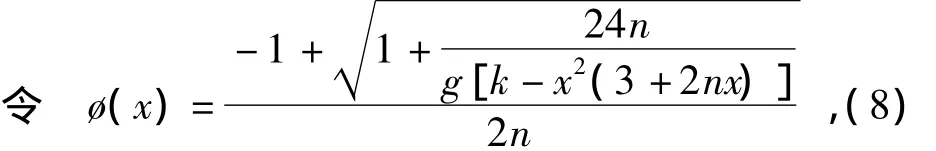
故|ø'(y)|＜1，所以迭代公式都是收敛的。

5 迭代公式初值的选取

迭代计算的精度及收敛速度，不仅与迭代格式有关，而且与迭代初值选取有关，只有合理的迭代初值与合理的迭代格式配套使用才能提高计算效率和精度。

由共轭水深的水流特点，可得到水跃方程的近似公式为

5.1 跃后水深的初值y0

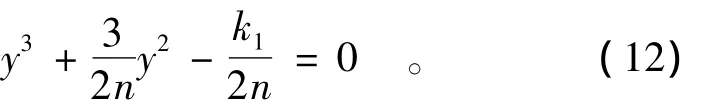
当Δ＞0时，方程(13)的一个正实根［5］为

故可得到跃后水深的初值为

当Δ＜0时，方程(13)的一个正实根为

故可得到跃后水深的初值为

5.2 跃前水深的初值x0

若已知跃后水深y，则可求出y2(3+2ny)，并令k2=y2(3+2ny)，代入式(11)中得

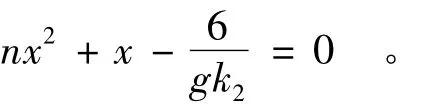
上式为一元二次方程，故可得到跃前水深的初值为

6 水跃共轭水深的直接计算公式及精度评价

确定了恰当的迭代初值后，就可以利用迭代公式得到其直接计算公式，即

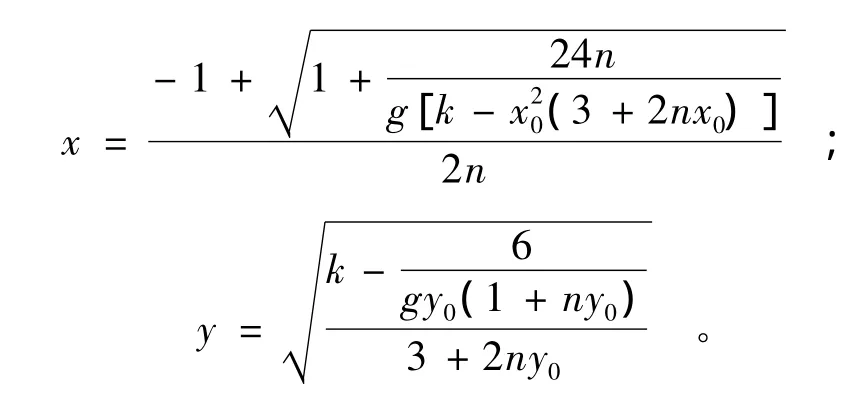
为了评价该直接计算公式的精确性，下面列出了在工程上常用范［0，3］内，共算出很多组x与y的值。因篇幅所限，本文仅列出部分数值组，见表1。

7 应用举例

一水跃产生于一棱柱体梯形水平渠段中，已知:流量Q=6.0m3/s，边坡系数m=1.0，b=2.0m，h1=0.4m。求跃后水深 h2。

(1)计算跃后水深的初值y0。

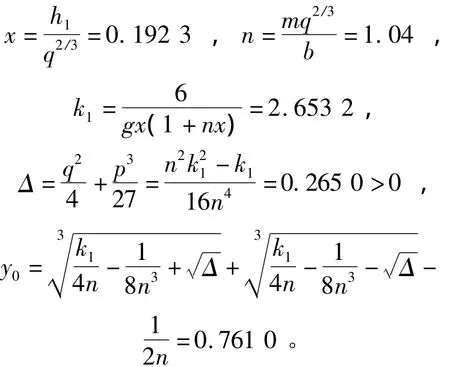
(2)迭代求解。

表1 共轭水深直接计算法精度评价表Table 1 Accuracy assessment of the calculated conjugate water depth in trapezoidal channel

(3)用冯家涛公式［6］、刘玲公式［7］和张小林公式［8］分别计算本例题，计算结果列于表2中。

表2 不同计算方法误差比较表Table 2 Comparison of calculated results and relative errors of different methods

利用参考文献［1］中提供的公式计算出的无量纲跃后水深与刘玲公式一样，也为0.714 1，相对误差为0.29%。

8 结语

梯形明渠共轭水深的计算问题其实质是求解2个高次方程，显然没有直接的解析解。基于此，本文利用传统的迭代法，首先通过求解一元二、三次方程得到共轭水深的初值近似公式;然后以此为初值，用迭代公式进行一次迭代得到梯形明渠共轭水深的直接计算公式。应用直接计算公式来计算梯形明渠水跃的共轭水深，不但公式形式简捷、直观，计算方便，且精度完全符合工程计算要求，值得工程技术人员采用。

［1］吴持恭.水力学［M］.北京:高等教育出版社，1979.(WU Chi-gong.Hydraulics［M］.Beijing:High Education Press，1979.(in Chinese))

［2］吕宏兴，裴国霞，杨玲霞.水力学［M］.北京:中国农业出版社，2002.(LV Hong-xing，PEI Guo-xia，YANG Ling-xia.Hydraulics［M］.Beijing:China Agriculture Publishing Press，2002.(in Chinese))

［3］辛孝明.平底梯形明渠水跃共扼水深的直接计算法［J］.山西水利科技，1997，117(3):59－63.(XIN Xiaoming.The Direct Calculation of the Conjugate Depth of the Trapezoidal Channel with Flat Bottom［J］.Shanxi Hydraulic Science＆ Technology，1997，117(3):59－63.(in Chinese))

［4］邓建中，葛仁兴，程正兴.计算方法［M］.西安:西安交通大学出版社，1992.(DENG Jian-zhong，GE Renxing，CHENG Zheng-xing.Methods of Calculation［M］.Xi’an:Xi’an Jiaotong University Press，1992.(in Chinese))

［5］华罗庚.高等数学引论［M］.北京:科学出版社，1974.(HUA Luo-geng.Advanced Mathematics Introduction［M］.Beijing:Science Press，1974.(in Chinese))

［6］冯家涛.梯形渠道水跃共扼水深直接计算公式［J］.海河水利，1998，(5):32－33.(FENG Jia-tao.The Direct Formula of the Conjugate Depth of the Trapezoidal Canal［J］.Haihe River Water Conservancy，1998，(5):32－33.(in Chinese))

［7］刘 玲，刘伊生.梯形渠道水跃共扼水深计算方法［J］.北方交通大学学报，1999，23(3):44－47.(LIU Ling，LIU Yi-sheng.Calculating Method for Conjugate Depth of Hydraulic Jump in Trapezoidal Channels［J］.Journal of Northern Jiaotong University，1999，23(3):44－47.(in Chinese))

［8］张小林，刘惹梅.梯形断面渠道水跃共扼水深的计算方法［J］.水利与建筑工程学报，2003，1(2):41－43.(ZHANG Xiao-lin，LIU Re-mei.Method of Calculation for Conjugate Water Depth of Water Jump in Trapezoid Channel［J］.Journal of Water Resources and Architectural Engineering，2003，1(2):41－43.(in Chinese))