突然扩散水跃方程的改进与比较
(1.西安理工大学 省部共建西北旱区生态水利国家重点实验室, 西安 710048;2.嘉兴学院 建筑工程学院, 浙江 嘉兴 314001; 3.上海大学 建筑系, 上海 200444)
1 研究背景
泄水建筑物下游的消能防冲是泄水建筑物水力设计中的重要问题[1-3]。由于建坝区域的地质、地形条件及水力条件不同,可以布置成不同的消能形式。水跃消能作为传统的消能形式被广泛采用[4-8]。水跃分为棱柱体明渠的水跃和空间水跃,水平渠底渐扩明渠段中的水跃[8-13]和水平渠底突然扩大明渠段的水跃(以下简称“突然扩散水跃”)[14-17]是适合扩散河槽的2种不同的空间水跃。
由于空间水跃流动复杂[18-21],空间水跃引起了相关研究者予以关注。而水平渠底突然扩散水跃的研究较少。关于水平渠底突然扩散水跃水力设计中的重要参数共轭水深比的计算,一类是依赖于试验资料建立的经验公式,这类公式由于受试验资料范围的限制,都有相应的应用范围,使用中也因此受到限制;另一类是借助于动量守恒原理建立的水平渠底突然扩散水跃方程(共轭水深方程)。根据共轭水深方程进行求解获得共轭水深比η(η=h2/h1,h1,h2分别为跃前、跃后断面水深)。后者力学概念清楚,但在推导过程中要引入一些假定,例如,必须假定回流平均水深。因此,根据回流平均水深假设的不同,就可得到不同的水平渠底突然扩散水跃方程。
基于上述研究背景,本文研究突然扩散水跃方程的特性。在回流区平均水深作为代表水深的假设下,根据动量守恒原理推导突然扩散水跃的一般方程。在改进了回流区平均水深具体表达式的基础上,得到突然扩散水跃的新方程,并给出有关参数的确定方法。并将已有的突然扩散水跃方程求得的共轭水深比与试验结果进行比较。

图1 突然扩散水跃Fig.1 Hydraulic jump in abruptly expanding channel
2 突然扩散水跃方程
图1是水平渠底突然扩散水跃的流动示意图。图中:h1,h2分别为跃前、跃后断面水深;h3为回流区平均水深;b,B分别为上游、下游渠槽宽度;v1为跃前断面的平均流速;v2为跃后断面的平均流速;P1为跃前断面的动水总压力;P2为跃后断面的动水总压力;P3为水跃始端扩散断面上的动水总压力。
对于图1所示的流动,忽略明渠槽底壁面的摩擦阻力,在突然扩散水跃的流动方向对图1的跃前与跃后两控制断面应用动量守恒原理,有
(1)
式中:Q为流量;γ为水的重度;g为重力加速度;α01为跃前断面的动量修正系数;α02为跃后断面的动量修正系数。
考虑跃前断面上的动量修正系数与跃后断面上的动量修正系数均为1.0,有
α01=α02=1.0 。
(2)
由连续性方程,有
(3)
假定跃前与跃后两断面上的水流为渐变流,水压力按静水压力分布,跃前断面的动水总压力为
(4)
跃后断面的动水总压力为
(5)
始端扩散区壁面压强依赖于回流平均水深,而回流水深沿始端扩散区壁面是变化的,一般假定用回流平均水深作为代表,这时,水跃始端扩散断面上的动水总压力为
(6)
将式(2)至式(6)代入式(1),得
(7)
(8)
式中h3为回流区平均水深。式(8)即为突然扩散水跃的共轭水深的一般方程。
3 突然扩散水跃方程的改进
3.1 已有的突然扩散水跃方程
回流区平均水深确定以后,代入式(8)就可以得到突然扩散水跃的共轭水深方程,然后求解突然扩散水跃的共轭水深方程就可以得到共轭水深比。对于回流区平均水深,研究者通常作出了一些假设,从而得到了相应的突然扩散水跃的共轭水深方程。 文献[14]假定回流区平均水深h3=h1,则有
(9)
文献[18]假定回流区平均水深h3=0.5(h1+h2),则有
βη(η-1)(3βη+β+η+3)-
(11)
3.2 突然扩散水跃方程的改进

αβη(β-1)(1+η2)=0 。
(12)
根据文献[16]和文献[18]关于回流区平均水深h3、跃前水深h1、跃后水深h2的试验资料,对系数α的变化规律进行了分析。系数α可以表示为
α=-0.066 9β2+0.484 6β-0.329 。
(13)
方程(12)的显式解为
4 不同突然扩散水跃方程求得的共轭水深比与试验结果的比较
将不同突然扩散水跃方程求得的共轭水深比与试验结果进行比较,以检验方程精度。利用式(9)—式(12)对文献[16]和文献[18]中90组试验资料进行了计算,共轭水深比的计算结果与试验结果的比较如图2所示。图2形象地给出了不同方程的计算结果与试验数据的差别。不同方程的计算结果与试验结果的有关参数的比较见表1—表3。
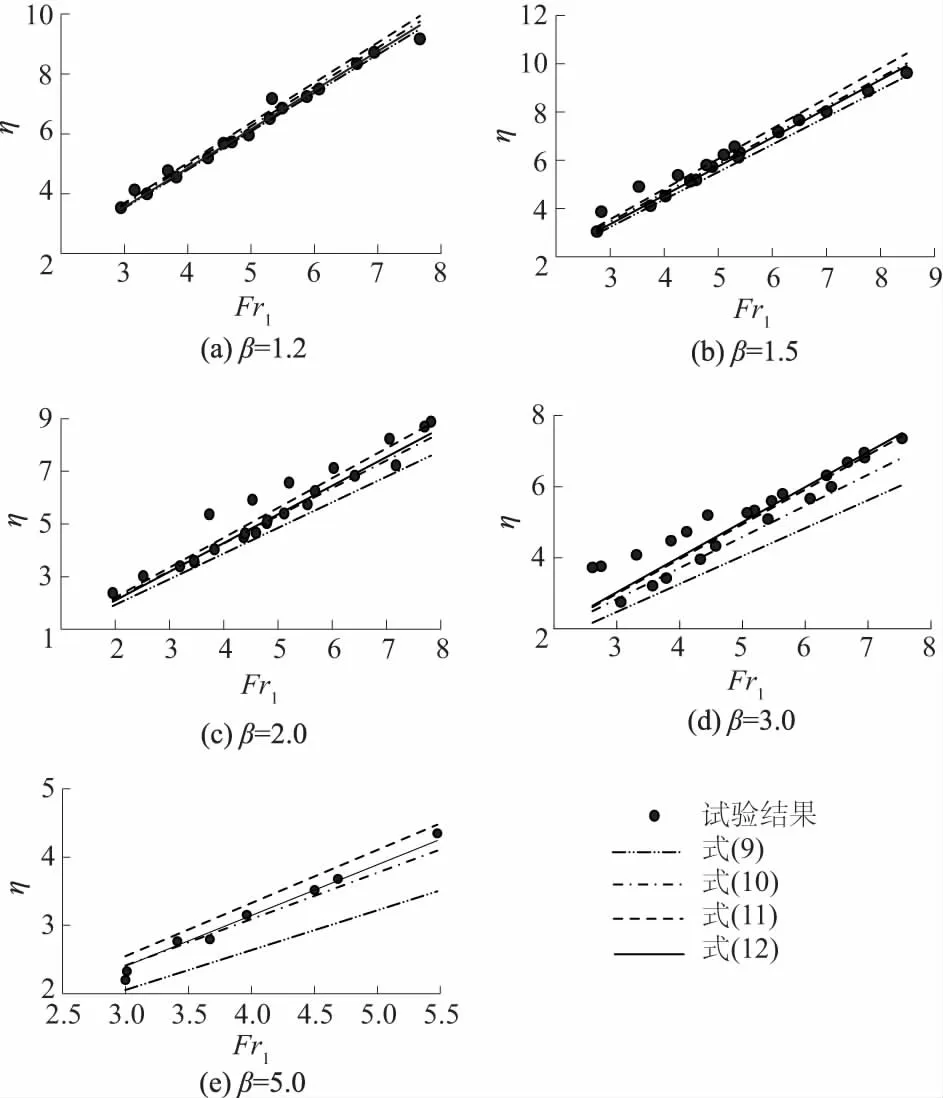
图2 不同方程共轭水深比的计算结果与试验结果的比较Fig.2 Conjugate depth ratio calculated by differentequations and experimental result

方程平均相对误差/%最大相对误差/%方程平均相对误差/%最大相对误差/%式(9)11.80640.841式(11)6.33132.420式(10)6.76129.206式(12)5.48528.210
(1)由图2可知,β=1.2时,式(9)—式(12)的计算结果接近。β=1.5时,当Fr1较小情况下,式(9)—式(12)的计算结果接近,当Fr1较大情况下,式(9)、式(11)的计算结果偏离式(10)、式(12)的计算结果。β=2.0时式(10)与式(12)的计算结果接近。β=3.0时式(11)与式(12)的计算结果接近,式(9)与式(10)的计算结果明显偏离。β=5.0时式(10)与式(12)的计算结果接近,式(9)与式(11)的计算结果明显偏离。
(2)由表1可以看出,对于在90组试验资料中关于不同方程共轭水深比的计算结果与试验结果的误差,式(9)的平均相对误差和最大相对误差最大,式(10)的平均相对误差次之,改进后的式(12)的平均相对误差和最大相对误差最小。

表2 不同突扩比时不同方程共轭水深比的计算结果与试验结果的相对误差Table 2 Errors between conjugate depth ratios calculated by different equations and experimental result inthe presence of varying abruptly expanding ratio

表3 不同相对误差范围的试验组次分布Table 3 Test groups in different error ranges
(3)由表2可以看出,不同突扩比时不同方程共轭水深比的计算结果与试验数据的比较说明,式(9)—式(12)都在β=3.0时平均相对误差和最大相对误差最大,式(9)—式(12)都在β=1.2时平均相对误差和最大相对误差最小。各个方程的相对误差变化规律基本相同。说明β=3.0时流动比较复杂。
(4)由表3可以看出,在90组试验资料中,共轭水深比的计算结果与试验结果的相对误差<5%的试验组次,式(9)有25次,组次最少;式(12)有57次,组次最多。相对误差>30%的试验组次,式(9)有5次,组次最多;式(10)和式(12)没有相对误差>30%的试验数据出现。式(12)与式(10)的比较说明,相对误差<5%的试验组次,由式(10)的41组次增加到式(12)的57组次,改进后的方程共轭水深比的计算结果与试验结果的相对误差明显减小。
(5)综上分析,改进后的式(12)在不同的突扩比情况下,共轭水深比的计算结果与试验结果的平均相对误差最小,计算精度最高。建议对于实际的工程计算问题可以采用式(12)进行。
(6)式(9)—式(12)在β=1.0时都简化成矩形明渠二元水跃的共轭水深方程。
5 结 论
本文研究了突然扩散水跃方程的特性,并将其与试验结果进行了比较,可以得出以下结论。
(1)在回流区平均水深作为代表水深的假设下,根据动量守恒原理推导了突然扩散水跃的一般方程。
(2)在改进了回流区平均水深具体表达式的基础上,得到了突然扩散水跃的新方程,并给出了有关参数的确定方法。
(3)将已有的突然扩散水跃方程求得的共轭水深比与试验结果进行了比较,在90组试验资料中,式(9)的平均相对误差和最大相对误差最大,改进后的式(12)的平均相对误差和最大相对误差最小。式(9)—式(12)都在β=3.0时平均相对误差和最大相对误差最大,都在β=1.2时平均相对误差和最大相对误差最小。改进后的式(12)在不同的突扩比情况下平均相对误差都最小,计算精度最高。
(4)在90组试验资料中,共轭水深比的计算结果与试验结果的相对误差<5%的试验组次,式(9)有25次,组次最少;式(12)有57次,组次最多。改进后的方程共轭水深比的计算结果与试验结果的相对误差明显减小。
(5)式(9)—式(12)的比较表明,改进后的式(12)共轭水深比的计算结果与试验结果的平均相对误差和最大相对误差最小,计算精度最高,且有显式解,计算方便。因此,建议用改进后的式(12)进行突然扩散水跃共轭水深的水力设计。

