基于线性矩法的短历时暴雨频率分布研究

(西北农林科技大学 水利与建筑工程学院，陕西 杨凌 712100)

1 研究背景

暴雨灾害是我国目前面临的最主要的气象灾害之一，由其引发的山洪、滑坡、泥石流、水土流失和内涝等灾害，严重威胁着人民的生命财产安全。针对暴雨的相关研究一直是国内外水文和气象领域的研究重点，其研究成果对我国的防洪减灾工作有重大意义。对于暴雨统计特性的研究可以揭示其在时间上的变化规律，其中选择反映地区暴雨特性的暴雨频率分布是得到准确合理的设计暴雨的首要条件，在工程实践中起着至关重要的作用，特别是对于短历时暴雨频率分布的选择更是研究的重点。

我国幅员辽阔，气候和地形条件复杂，各地在工程实践中对于暴雨频率分布的选择无法达成共识。李松仕[1]在早期研究中指出，皮尔逊Ⅲ型分布弹性较大，适用于我国南北方大部分地区；邓培德[2]在对全国10个代表站的暴雨资料进行拟合后，指出指数分布在暴雨量序列的拟合上效果要优于皮尔逊Ⅲ型分布；金光炎[3]认为广义极值分布在我国水文资料的拟合上具有良好的适应性，特别是其离均系数表对水文频率分析和各类统计计算有重要意义；蔡敏等[4]采用耿贝尔分布对我国东部降水量极值进行了拟合，效果理想，适用性强。大量科研工作者的研究表明，选择适宜当地情况的暴雨频率分布在各地工程实践中有着至关重要的作用。陕西省为洪涝灾害多发省份，由暴雨导致的洪涝灾害更是频繁发生，给人们的正常生活带来诸多不利影响，造成了巨大经济损失和资源浪费。针对陕西省短历时暴雨频率分布的研究可以为城市防洪、排涝规划以及相关工程设计的雨量计算提供参考，可以指导当地工程实践。

2 资料与方法

2.1 资 料

本文所用资料为陕西省气象信息中心提供的省内18个基准气象站和基本气象台站1984—2013年的实测暴雨资料，各气象台站基本情况见表1，表1中前11个站点位于秦岭以北，后7个站点位于秦岭以南。针对实测资料中存在的个别时段缺测问题，直接移用邻近站点同年实测值进行插补。

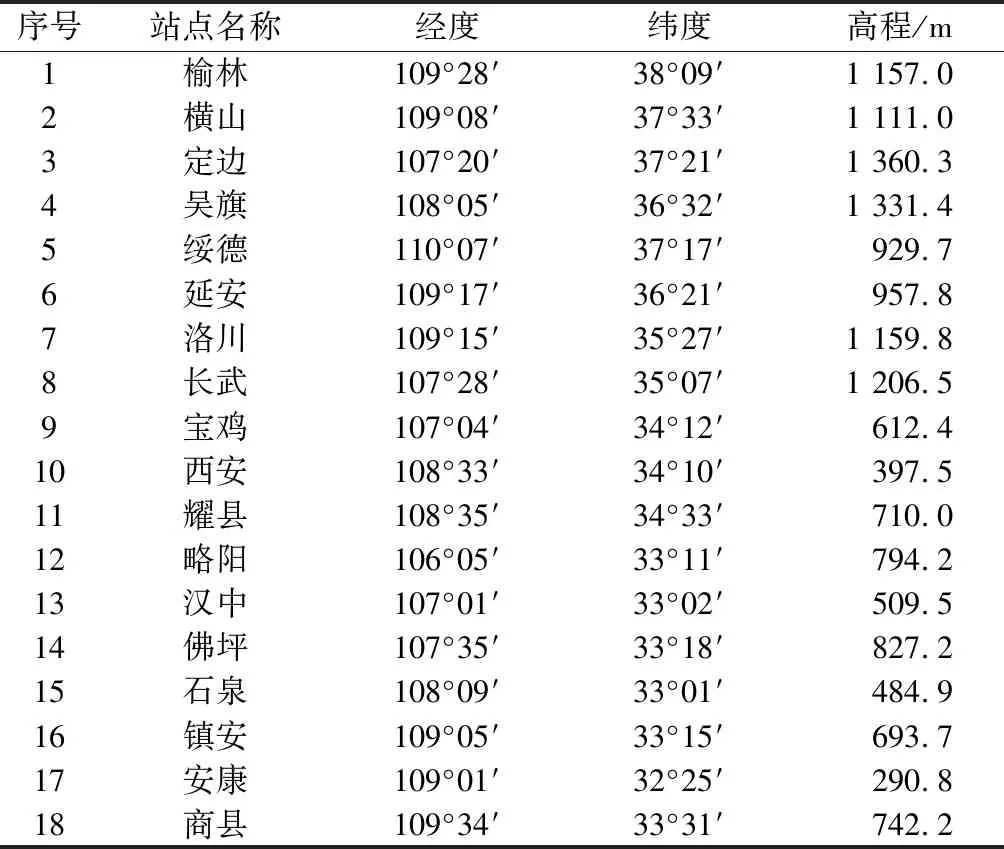
表1 分析依据站点基本情况Table 1 Basic information of the meteorological stations

2.2 研究方法

2.2.1 暴雨资料统计选样

现今国内常用的选样方法有年最大值选样法、超定额选样法和年超大值选样法。考虑到现阶段已有水文资料的积累已经满足研究需要，故采用年最大值选样法对各历时的暴雨资料进行选样，这不仅与国际上通用的暴雨资料选样方法相符，而且与频率及重现期的定义相吻合[5-6]。

2.2.2 备选频率分布

在前人研究的基础上，综合考虑短历时暴雨的特性和各频率分布的弹性、适应性等因素，选取水文统计上常用的皮尔逊Ⅲ型分布(Pearson Ⅲ distribution，P-Ⅲ)、广义极值分布(Generalized Extreme Value distribution，GEV)、耿贝尔分布(Gumbel distribution，Gumbel)、正态分布(Normal distribution，N)、指数分布(Exponential distribution，EXP)和两参数伽马分布(Gamma distribution，Gamma)作为本次研究的备选频率分布[7]。

2.2.3 参数估计

目前在水文统计上常采用的参数估计方法有矩法、极大似然法和概率权重矩法等。矩法是一种经典的参数估计方法，其构造估计量的原理和方法相对简单，但其在进行高阶矩计算时会不可避免扩大自身误差；极大似然法是建立在极大似然原理基础上的一种统计方法，但其似然函数与分布本身有关，构造较为困难；Greenwood等[8]在1979年提出的概率权重矩法被认为是一种有效的普适性很强的参数估计方法，在一定程度上改善了矩法和极大似然法在参数计算结果上的误差，但是在实践应用中发现该方法仍存在稳健性和不偏性不足的问题。

Hosking[9]于1990年进一步提出了线性矩的概念，定义次序统计量线性组合的期望值为线性矩，这是对概率权重矩的一种改进。线性矩法在参数估计上表现出了高稳健性和高精度的特点，特别是它对水文序列中的极大值和极小值远没有常规矩那么敏感，这在一定程度上解决了短历时暴雨量序列中存在的极大值问题。在实际应用时，线性矩法只需利用序列资料进行加减运算，大大降低了序列本身所存在的误差，也降低了常规矩法在计算偏态系数时利用三阶矩所产生的误差[10-12]。Wang[13]据此提出了针对离散序列线性矩的直接估算方法，使计算过程更为简捷，具体计算方法为

(1)

在线性矩已知情况下，可以通过各序列的线性矩及其线性矩系数对各备选频率分布的参数进行计算，具体计算方法详见文献[14]。

2.2.4 优选指标

2.2.4.1 确定性系数(QD)

QD是用来描述实测值与假设分布理论值拟合程度的统计特征量。QD值越接近于1，证明实测数据与对应分布的理论值线性关系越强，拟合程度越好。QD值计算简便，敏感性较好，是频率分布优选中最常用的方法之一。其计算方法为

(2)

2.2.4.2 误差平方和(RMSE)

RMSE即观测值与假设分布理论值的均方根误差，以其结果最小来判定最优分布。RMSE对2组数据的特大或特小误差反应非常敏感，在频率分布优选中的应用十分广泛[15]。其计算方法为

(3)

2.2.4.3 概率点据相关系数r(PPCC)

PPCC是根据排序后的实测序列和经验频率推求出假设分布对应的期望值，然后得出2组序列的相关系数r。类似于确定性系数，r值越接近1，2组序列线性关系越强，拟合效果越好。其计算方法为

(4)

3 实例研究

3.1 线性矩系数时空变化

对各分析站点采用年最大值选样法分别选取了10，30，60，90，120 min共5个历时的暴雨量序列，利用线性矩法估计的各暴雨量序列线性矩系数结果见表2。

各站点暴雨量序列的均值随着历时增加呈增加趋势，但增幅逐渐下降，即暴雨强度随历时增加呈明显降低趋势；而在空间上，各站点暴雨量序列均值离散程度随历时增加呈递增趋势，通过空间插值方法绘制5个短历时暴雨量均值等值线图，发现各历时暴雨量序列均值自西向东均存在逐渐增大趋势，暴雨量较大区域集中在耀县、佛坪和石泉附近，较小的区域集中在横山、宝鸡和西安附近。限于篇幅，本文仅给出90 min暴雨量序列均值等值线图，见图1(a)。

表2 研究区各暴雨量序列线性矩系数Table 2 Values of linear moment coefficient of each rainstorm sequence

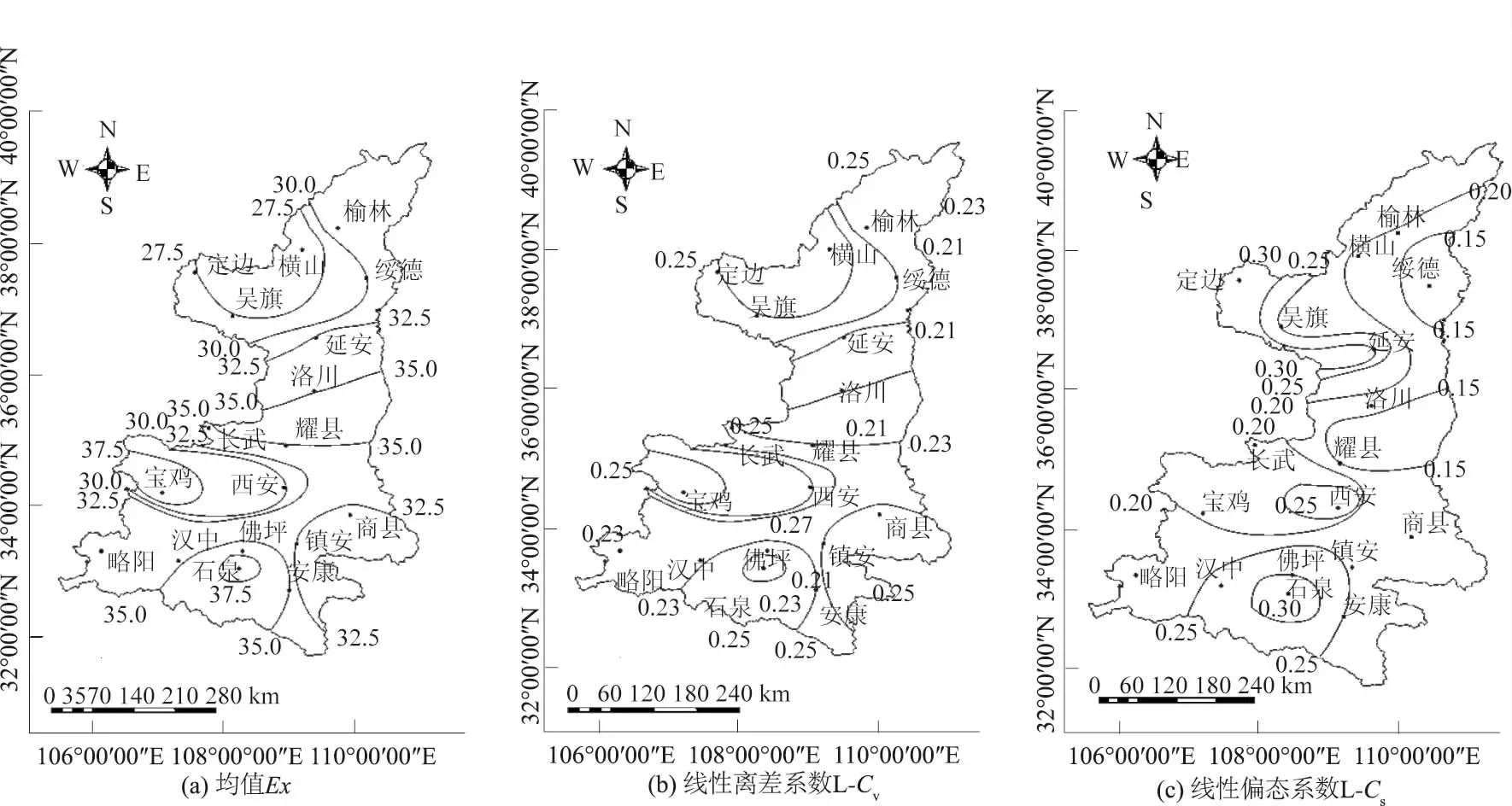
图1 研究区暴雨量序列线性矩系数等值线图(历时t=90 min) Fig.1 Contours of linear moment coefficient of rainstorm sequences(t=90 min)

各站点暴雨量序列线性离差系数L-Cv值在10～30 min内随历时的增加呈现出增加趋势；30～90 min内有10个站点呈增加趋势，5个站点呈减少趋势；90～120 min时，有13个站点的L-Cv值呈减少趋势，5个站点呈增加趋势；从5个历时看，有12个站点总体呈增加趋势。在空间上，各站点暴雨量序列L-Cv值的离散程度随历时增加呈递减趋势，区域一致性增强；同时L-Cv等值线图表现出秦岭以北自西向东呈递减趋势，秦岭以南则呈现出中部高、东西低的态势，见图1(b)。

各站点暴雨量序列线性偏态系数L-Cs值在10～120 min有3个站点呈增加趋势，1个站点呈下降趋势，4个站点呈先增加后降低趋势，5个站点呈先减少后增加趋势，另有5个站点变化趋势不明显，可见各站点暴雨量序列线性偏态系数L-Cs值随历时变化无统一趋势。在空间上，各站点暴雨量序列L-Cs值的离散程度随历时增加呈递减趋势，区域一致性增强；同时L-Cs等值线图反映出秦岭以北自西向东呈递减趋势，秦岭以南则呈现出中部高、东西低的态势，与L-Cv值趋势一致,见图1(c)。

3.2 频率分布优选

通过暴雨量序列的线性矩和线性矩系数计算各备选频率分布的参数。分别采用QD,RMSE和r为指标对各暴雨量序列的最优频率分布进行选取。对结果进行分析发现，3种优选指标在最优频率分布的选择结果上完全一致，进一步证明了优选结果的可靠性。不同历时暴雨量序列中，各备选频率分布为最优分布的占比如表3所示。

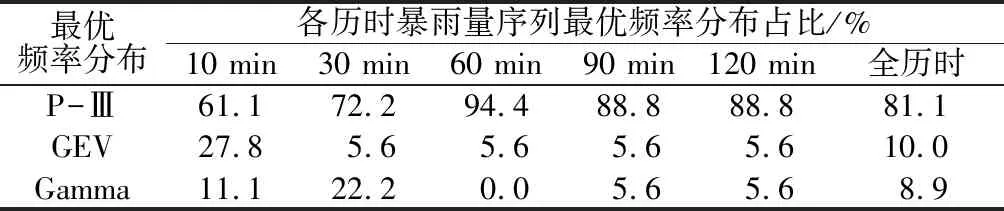
表3 研究区各历时暴雨量序列最优频率分布统计Table 3 Statistics of optimal frequency distribution ofrainstorm sequences of different durations

由表3可知，在10 min的序列中，最优分布为P-Ⅲ分布的序列占总序列组数的61.1%，GEV分布占27.8%，Gamma分布占11.1%；在30 min的序列中，最优分布为P-Ⅲ分布的序列占总序列组数的72.2%，GEV分布占5.6%，Gamma分布占22.2%；在60 min样本中，最优分布为P-Ⅲ分布的序列占总序列组数的94.4%，GEV分布占5.6%；90 min和120 min的序列中，最优分布为P-Ⅲ分布的序列占总序列组数的88.8%，GEV和Gamma分布各占5.6%。随着历时的增加，最优分布为P-Ⅲ分布的比重逐渐增加。对全部历时序列而言，最优分布为P-Ⅲ分布的序列占总序列组数的81.1%， GEV分布占10%，Gamma分布占8.9%。

在优选指标的基础上，结合计算暴雨量和实测暴雨量相关图，可以更形象地反映各备选频率分布拟合情况。如图2所示，各备频率选分布中整体拟合效果最优的为P-Ⅲ分布；Gamma分布的拟合效果仅次于前者的拟合效果，且2种分布拟合效果相差不大；相对于前2种分布，GEV和N分布的整体拟合效果有明显劣势；Gumbel和EXP分布的整体拟合效果最差，二者计算暴雨量均要低于实测值，特别是Gumbel分布的计算值中出现了大量负值，有悖暴雨的物理机制，不能予以采用。

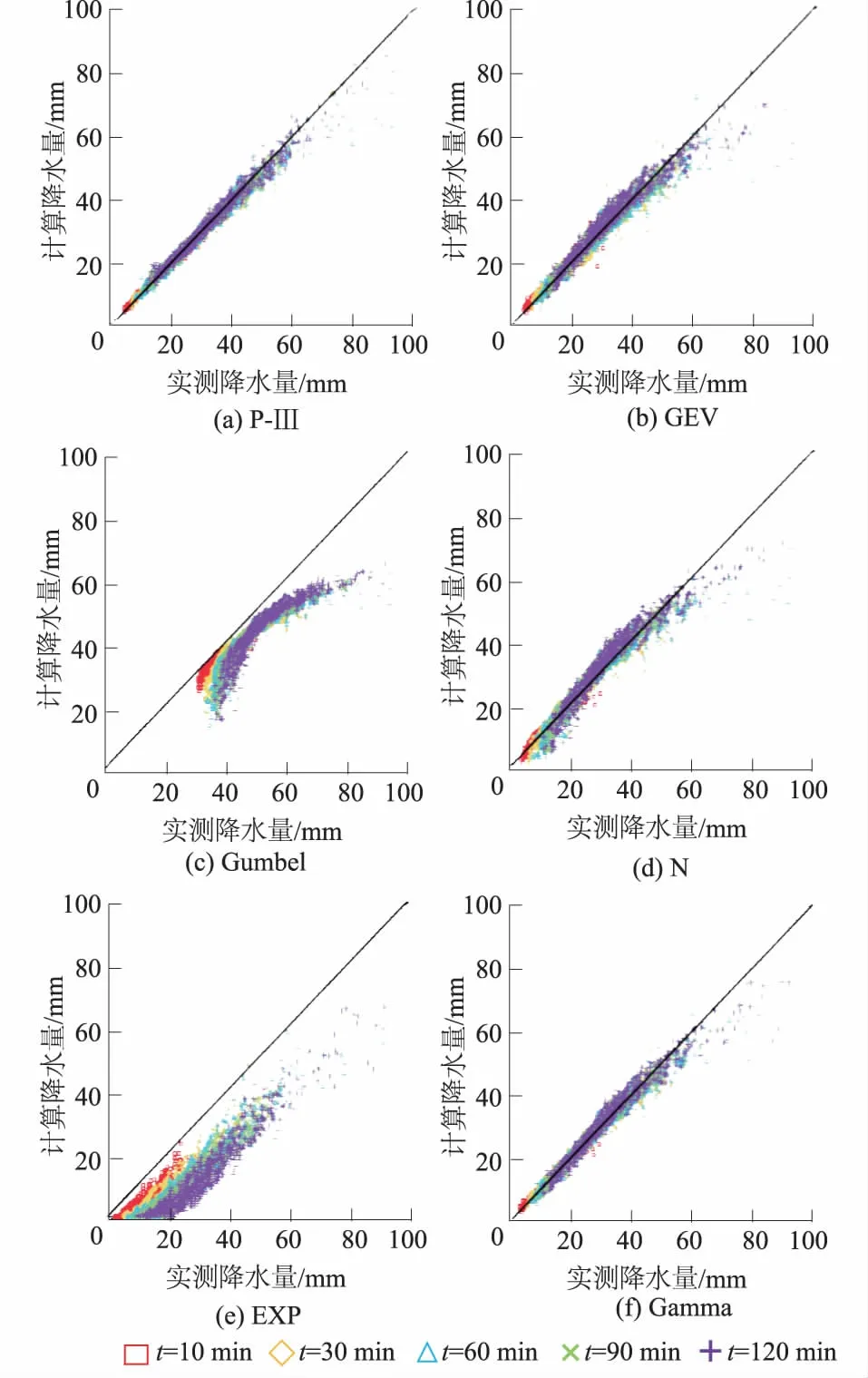
图2 实测暴雨量与各备选分布计算暴雨量相关图Fig.2 Correlation between measured rainfalland calculated rainfall of alternative distributions

在研究中发现，部分以P-Ⅲ分布为最优频率分布的序列中会出现其位置参数a0为负数的情况，这与暴雨的物理机制不相符，但这些序列的第二优势分布均为Gamma分布。在学术和工程实践中如果遇到上述情况，通常采用的方法是将其位置参数a0认定为0，并采用两参数的Gamma分布作为该序列的最优频率分布。Gamma分布可以看作是位置参数为0的特殊的P-Ⅲ分布，二者在概率密度函数上基本一致，属于一类分布。如表4所示，以P-Ⅲ分布(包含Gamma分布)为最优分布的序列为81组，占到总序列组数的90.0%，且通过比较发现以GEV分布为最优分布的序列中，P-Ⅲ或Gamma分布的拟合效果与GEV分布的拟合效果相差甚微。综上考虑，认定P-Ⅲ分布(Gamma分布)为研究区短历时暴雨的理论频率分布。

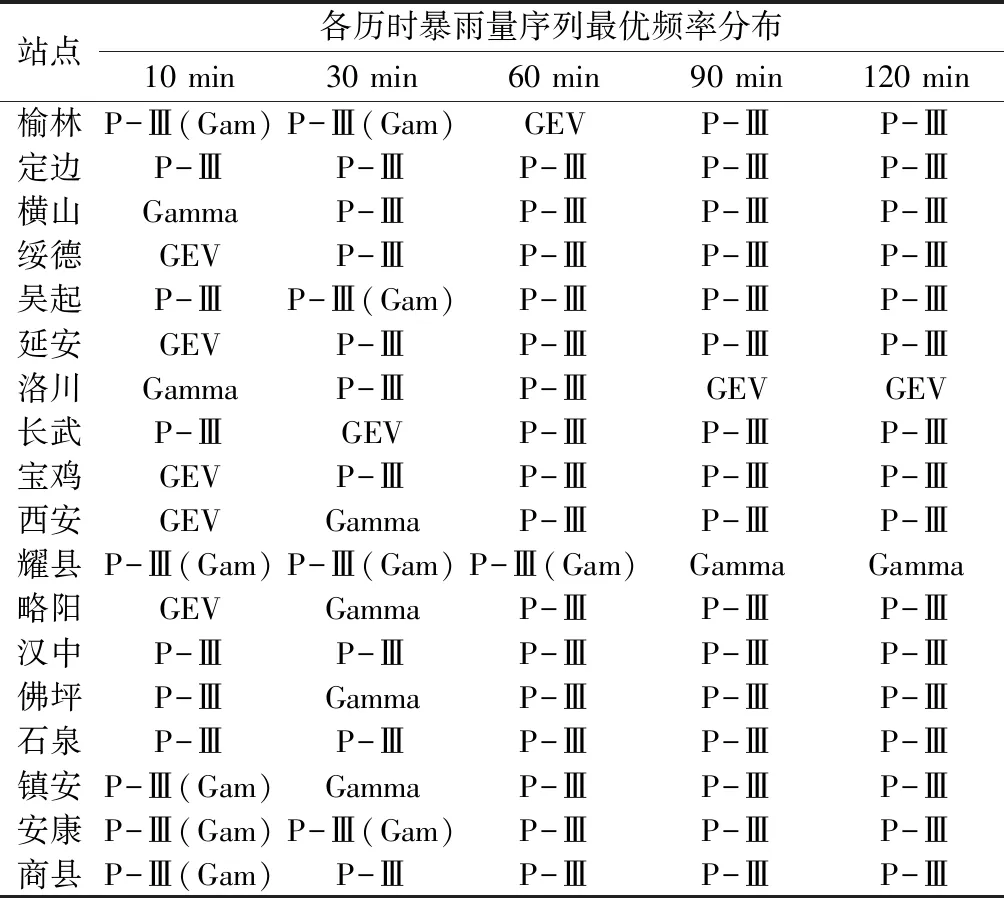
表4 各站点暴雨量序列最优频率分布统计Table 4 Statistics of optimal frequency distribution forrainstorm sequence at each station

注：P-Ⅲ(Gam)对应序列的最优频率分布为P-Ⅲ分布(位置参数为负)，第二优势分布为Gamma分布

4 结 论

(1)研究区各站点暴雨量序列期望随历时增加呈增长趋势，但其增幅逐渐降低；暴雨强度随历时下降明显，但下降幅度逐渐降低；同历时各站点暴雨量序列均值和平均暴雨强度自西向东均呈逐渐增加趋势。

(2)研究区18个分析站点中有12个站点的暴雨量序列线性离差系数L-Cv随历时增加整体呈增长趋势，但增幅逐渐降低；各站点暴雨量序列L-Cv离散程度随历时增加不断减小，区域一致性增强；秦岭以北L-Cv值自西向东呈递减趋势，秦岭以南L-Cv值则呈现出中部高、东西低的态势。

(3)研究区各站点暴雨量序列线性偏态系数L-Cs值随历时变化无统一趋势；各站点暴雨量序列L-Cs的离散程度随历时增加不断减小，区域一致性增强；秦岭以北L-Cs值自西向东呈递减趋势，秦岭以南L-Cs值则呈现出中部高、东西低的态势，与L-Cv值趋势一致。

(4)以P-Ⅲ分布(包含Gamma分布)为最优分布的暴雨量序列为81组，占总序列组数的90.0%，可作为研究区短历时暴雨的理论频率分布。