结构可靠度理论在水工结构设计标准中的应用

(武汉大学 土木建筑工程学院，武汉 430072)

1 研究背景

在水工结构设计领域，自我国第二层次的国家标准《水利水电工程结构可靠度设计统一标准》(GB 50199—1994)[1]于1994年颁布实施以来，水工结构设计规范按照此标准关于结构可靠度理论的相关规定已进行了大规模的修编[2-6]。我国采用结构可靠度理论的水工结构设计规范[7-11]，有的已经颁布实施，有的已完成了第二轮修订或正在进行第三轮修订[12-16]。

为了进一步推动结构可靠度理论在水工结构设计规范中的应用与发展， 本文介绍了结构可靠度理论在国内外工程结构设计标准中的应用与发展概况， 重点对结构可靠度理论在水工结构设计规范中应用的成功经验进行了归纳与总结， 供水工结构设计规范按结构可靠度理论进行修编时借鉴与参考。

2 结构可靠度理论在国内外工程结构设计标准中的应用

安全可靠与经济合理始终是结构设计的基本原则[17-20]。在保证结构安全可靠前提下的经济性，永远是结构工程师所追求的目标。采用以结构可靠度理论为基础的概率极限状态设计法，可以更全面地考虑影响结构可靠度的主要因素的客观变异性，在安全与经济之间寻求最佳平衡，实现优化设计。因此，近年来概率极限状态设计法在工程结构设计标准中已得到广泛的应用[21-24]，使结构可靠度理论的研究与应用进入了一个新的阶段[25-27]。

2.1 结构可靠度理论在国外工程结构设计标准中的应用

早在20世纪80年代初，国际上由7个著名的国际学术组织CEB，FIP，CIB，CECM，IABSE，IASS，RILEM等联合成立了国际安全度联合委员会JCSS，并于1981年提出了“General Principle on Reliability for Structures”的建议草案。在此基础上，国际标准化组织ISO于1986年正式发布了国际标淮《结构可靠性总原则》(ISO 2394:1986)，用于指导各国工程结构设计标准按概率极限状态设计法进行修编。1998年发布的ISO 2394:1998是这一国际标准的第2版[28]。与1986年版相比，概率极限状态设计法在国际上又有了新的进展。ISO 2394:1998首次明确提出了工程结构设计标准采用概率极限状态设计法和分项系数设计表达式的具体规定；首次明确提出了设计使用年限的概念和相应的设计规定。对于承载能力极限状态，建议目标可靠指标可分别采用3.1，3.8，4.3，与我国现行的几本工程结构可靠性设计统一标准建议的目标可靠指标取值相近[1,29-34]。ISO 2394的编制，在国际上有很大影响，很多国家有关结构设计标准的编制、修订都参考了该标准。

2015年出版的ISO 2394:2015“General Principle on Reliability for Structures ”[35]，是这一国际标准的第3版。与1998年版相比，2015年版的主要进展和变化如下：

(1)2015年版以一般经验为基础，提出了以合理方式确保结构或工程具有合适的可靠度水平的原则和方法。

(2)1998年版将安全性和可靠性主要放在结构的功能要求上，而2015年版则主要放在基于风险的考量和社会经济效益方面。

(3)2015年版特别强调了“结构整体稳固性(structural robustness)”的概念，给出了结构整体稳固性设计的相关规定。

(4)2015年版提供了3种水准的设计方法：风险已知的设计法(risk informed)；基于可靠度的设计法(reliability based)；半概率的设计法(semi-probabilistic)。

值得注意的是，ISO 2394:2015将以往定义的水准二的近似概率法(亦称以概率理论为基础的极限状态设计法)，明确归入到“半概率设计法”中。

欧洲标准化委员会CEN根据ISO 2394的原则，已编制了一整套采用概率极限状态设计法的《欧洲工程结构设计统一规范》[36-45]，共10卷58册，包括设计基础和结构上的作用、混凝土结构、钢结构、钢与混凝土组合结构、木结构、砌体结构、基础与岩土工程、结构抗震、铝结构等，其正式版本从2002年起已开始陆续发布[22,24]。

美国的结构设计标准是结构可靠度理论与应用研究的代表之一。1982年基于概率的荷载准则首次在美国国家标准A58.1—1982中得到应用[46]，它后来又以美国土木工程学会的标准ASCE 7出版发行，其最新版本为ASCE/SEI 7-10 “Minimum Design Loads for Buildings and Other Structures”[47]，自1982年至今一直为美国采用概率极限状态设计法的结构设计标准所引用，包括美国钢结构协会AISC的钢结构设计规范[48-49]和美国混凝土协会ACI 318的混凝土结构设计规范[50]。美国的这些主要结构设计标准都相继采用了基于结构可靠度理论的概率极限状态设计原则和分项系数设计表达式。

国外发达国家的工程结构设计标准，大都引入了基于结构可靠度理论的概率极限状态设计原则，按分项系数设计表达式进行设计。在工程结构设计标准中积极推广应用基于结构可靠度理论的概率极限状态设计原则和分项系数设计表达式，确已成为当代国际工程结构领域的一个共同的发展趋向[2]。

2.2 结构可靠度理论在国内工程结构设计标准中的应用

我国在工程结构可靠度研究领域，开展了大量的理论研究、资料收集和数据实测工作，全面总结了我国的工程实践经验，并借鉴了国际标准ISO 2394的有关规定。自1984年以来，先后编制并颁布了《建筑结构设计统一标准》(GBJ 68—1984)[29](第2轮修订版为《建筑结构可靠度设计统一标准》(GB 50068—2001)[30])、《工程结构可靠度设计统一标淮》(GB 50153—1992)[31]、《港口工程结构可靠度设计统一标准》(GB 50158—1992)[32]、《水利水电工程结构可靠度设计统一标准》(GB 50199—1994)[1]、《铁路工程结构可靠度设计统一标准》(GB 50216—1994)[33]、《公路工程结构可靠度设计统一标准》(GB/T 50283—1999)[34]，这些标准的最新版本分别为《建筑结构可靠性设计统一标准》(GB 50068—2018)[51]、《工程结构可靠性设计统一标淮》(GB 50153—2008)[52]、《港口工程结构可靠性设计统一标准》(GB 50158—2010)[53]、《水利水电工程结构可靠性设计统一标准》(GB 50199—2013)[54]、《铁路工程结构可靠性设计统一标准》(试行)(Q/CR 9007—2014)[55]。近30多年来，全国建筑、港口、水利水电、铁路和公路等行业的结构设计标准在上述“统一标准”的指导下，已进行或正在进行大规模的修订或编制[2，56-60]。目前我国各行业的结构设计标准大都采用了概率极限状态设计法，这项工作的规模和深度已超过了世界上一些发达国家的水平，大大提高了我国工程结构设计标准的科学水平，标志着我国在工程结构可靠度设计方面走在了世界先进水平的前列。

笔者自1988年参加《水利水电工程结构可靠度设计统一标准》和《水工混凝土结构设计规范》按结构可靠度理论编制和修编的专题研究以来[56-61]， 先后主持和参加完成了10余项工程建设国家标准和行业标准按结构可靠度理论修编的专题研究及相应的标准条文与条文说明的编写[62-72]。

采用基于结构可靠度理论的概率极限状态设计原则和分项系数设计表达式，可以较好地对结构中的主要不定性因素利用统计数学进行量化分析，为实现优化设计，在结构安全可靠与经济合理之间选择最佳平衡创造了条件，并且可以做到所设计的同类结构构件在不同的设计条件下均具有较佳的可靠度一致性。因此，在我国的水工结构设计标准中继续积极稳妥地推广应用基于结构可靠度理论的概率极限状态设计原则，符合当代国际工程结构标准的发展趋势。

3 结构可靠度理论在水工结构设计标准中的发展与应用

3.1 水工结构设计标准的可靠度校准和目标可靠指标的确定原则与方法

众所周知，结构设计标准修订的首要工作，就是规定恰当的安全度设置水平。新的安全度设置水平应当更为合理，但又不能偏离现行规范太远[73]。舒勒(Schueller)和梅尔彻斯(Melchers)在谈修订规范时说：“如果要有什么改变，只能是逐步的和微小的，以便不引起规范使用者的不安和苦恼。规范修订所导致的安全度水平的变化若大于10%，就常常会大得使实际工作者们恐慌，从而拒绝接受。”因此，国内外一般都是采用“校准法”(Calibrating)来分析现行标准结构设计的总体安全度水平，并据此来确定标准修订稿拟采用的安全度设置水平[2，56-60]。

关于“校准法”，可以有2种方式：一种是以现行标准为基准，用概率方法(一次可靠度分析法)反算出现行结构设计标准中隐含的可靠指标β，摸清现行标准结构设计的总体安全度设置水平，并据此确定新标准拟采用的目标可靠指标；另一种是以现行标准的分项系数设计表达式及相应的分项系数取值方案为基础，求出各种构件相应于分项系数设计表达式的相当安全系数(亦称综合安全系数)[2，56-57，64-65，69，71-72]，进而确定新标准拟采用的相当安全系数(或称“安全度设置水平”)。在可靠度校准分析或推求相当安全系数的过程中，还可以发现现行标准中个别构件的安全度设置水平过高或过低的不合理情况，作为标准修订时对构件的安全度设置水平进行局部调整的依据。

下面以水工混凝土结构设计规范为例，介绍水工混凝土结构设计规范的可靠度校准和目标可靠指标的确定原则与方法。当年《水利水电工程结构可靠度设计统一标准》(GB 50199—1994)在编制过程中，曾选择《水工混凝土结构设计规范》和《混凝土重力坝设计规范》作为试点，论证结构可靠度理论在水工结构设计标准中推广应用的可行性。

原《水工钢筋混凝土结构设计规范》(SDJ 20—78)[74]修订时作为《水利水电工程结构可靠度设计统一标准》(GB 50199—1994)编制过程中按结构可靠度理论进行修编的试点， 西北勘测设计研究院的黄振兴、 干城和原武汉水利电力学院的贺采旭、 侯建国及华北水利水电学院的程学文、 解伟等曾利用一次可靠度分析法， 对SDJ 20—78规范进行了可靠度校准分析， 有关研究成果已为《水利水电工程结构可靠度设计统一指标》(GB 50199—1994)[1]和《水工混凝土结构设计规范》(DL/T 5057—1996)[3]所采纳。 可靠度校准分析时选取了水工混凝土结构中常用的轴拉、 轴压、 受弯、 大偏压、 小偏拉、 梁受剪、 小偏压共7种典型构件， 考虑了5种不同的材料组合和5种不同的荷载组合及若干个常遇荷载效应的比值ρ； 求可靠指标β的平均值时， 还考虑了不同材料组合的加权系数； 对于不同的荷载组合、 不同的ρ值和延性、 脆性破坏构件的平均β及7种典型构件的总平均β，则采用了简单的算术平均。不同水工建筑级别的7种典型构件可靠度校准分析的汇总表及目标可靠指标βt的取值建议见表1，可靠度校准分析的主要结论如下，详请参阅文献[56]—文献[61]。

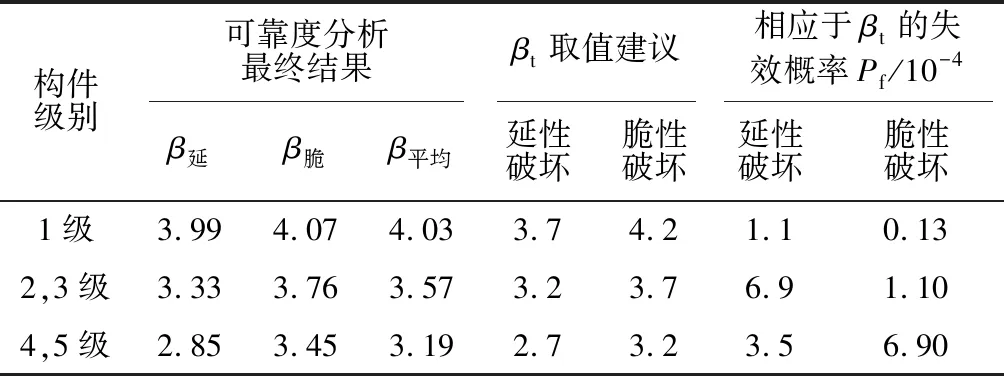
表1 水工混凝土结构可靠度校准分析结果汇总及βt取值建议Table 1 Summary of reliability calibration results for hydraulic concrete structure and recommended values of βt

(1)总体来说，属于同一破坏类型的构件的可靠指标相差并不悬殊。以2,3级构件为例，属延性破坏的轴拉、受弯和小偏拉构件，其β值大体在3.2±0.25范围内变化，而属于脆性破坏的轴压、小偏压和梁受剪等构件，其β值大体在3.7±0.25范围内变化。这就有可能在水工混凝土结构范围内分别就延性与脆性破坏构件规定统一的目标可靠指标[2，29]。

(2)若将2,3级构件的可靠度校准结果与《钢筋混凝土结构设计规范》(TJ 10—74)的可靠度校准结果作一比较[75-76]，则可发现水工钢筋混凝土2,3级构件的可靠指标与TJ 10—74的校准结果是比较接近的，但由于SDJ 20—78规范2，3级构件的强度安全系数比TJ 10—74规范相应构件的强度安全系数均大一些，使得2，3级构件可靠指标的平均值均较TJ 10—74规范相应构件的平均值略高一些，因而可以认为SDJ 20—78规范2，3级构件的安全度设置水平是基本合适的、可以接受的。

(3)参考《建筑结构设计统一标准》(GBJ 68—1984)[29]关于目标可靠指标的取值规定，若以2，3级构件的可靠度校准结果为基准，比较不同安全等级之间的可靠指标可知，延性破坏的β1-β2,3=0.66>0.5，β2,3-β4,5=0.47≈0.5，而脆性破坏的β1-β2,3=0.31<0.5，β2,3-β4,5=0.31<0.5，说明SDJ 20—78规范1级构件的β延偏高，而β脆偏低；4，5级构件的β延基本适中，而β脆偏高，规范修订时宜作适当调整。

从表1还可看出，同一安全等级中2，3级和4，5级构件的脆性破坏与延性破坏可靠指标的差值Δβ均在0.5左右，而1级构件的Δβ只有0.08，说明SDJ 20—78规范1级构件的安全系数取值不尽合理，即1级构件发生延性破坏时的安全系数K偏大，而脆性破坏时的安全系数K又偏小，规范修订时需作适当调整。

(4)根据SDJ 20—78规范可靠度校准分析的结果，文献[56]—文献[61]当时建议1级构件延性破坏的可靠指标β延应适当降低，脆性破坏的可靠指标β延应适当提高；4，5级构件发生脆性破坏时的可靠指标β延以及大偏压构件的可靠指标β亦可适当降低；其余构件则宜维持SDJ 20—78的安全度设置水平。上述文献所建议的水工混凝土结构设计规范修订稿目标可靠指标的取值已为《水利水电工程结构可靠度设计统一指标》(GB 50199—1994)[1]和《水工混凝土结构设计规范》(DL/T 5057—1996)[3]所采纳，见表1。

3.2 水工结构设计标准作用分项系数的确定原则和方法

长期以来水工结构设计的作用(荷载)取值一般均由各类水工结构设计标准分别作出规定，缺乏统一的取值标准和方法。按照《水利水电工程结构可靠度设计统一标准》(GB 50199—1994)[1]规定的概率极限状态设计原则，《水工建筑物荷载设计规范》(DL 5077—1997)[77]对适用于水工建筑物设计的作用取值标准和作用分项系数的取值作出了统一规定。DL 5077—1997的作用分项系数取值主要参考了“水工钢筋混凝土结构可靠度分析和分项系数确定——《水利水电工程结构可靠度设计统一标准》附件二”[56]和《水工混凝土结构设计规范》(DL/T 5057—1996)按可靠度理论修编的专题研究成果[57-61]。这里将《水工混凝土结构设计规范》(DL/T 5057—1996)[3]规定的作用分项系数取值方案作一简要介绍。

DL/T 5057—1996规定的作用分项系数是在按超载系数的概念确定的作用分项系数取值的基础上， 采用概率方法经优化计算并适当考虑工程经验优选确定的[56-61]。 优化作用分项系数时， 选择了水工混凝土结构中常用的7种典型构件， 考虑了5种不同的作用组合及若干个不同的作用效应比值ρ的影响。 优化的目标有2种： 其一是按所选定的γG,γQ进行设计时，各构件的计算可靠指标与规定的目标可靠指标之间总体上误差最小；其二是在确定γG,γQ的取值时， 还应满足各构件在不同的作用组合下的结构系数γd尽可能地相等或相近。 优化计算中估计永久作用分项系数的可能取值为γG=1.00, 1.05, … , 1.40，可变作用分项系数的可能取值为γQ=1.00, 1.05, … , 1.90， 故γG,γQ的可能取值共171组。 根据上述优化目标， 利用最小二乘法的优化原理， 从γG,γQ可能的171组取值中， 由给定的目标可靠指标， 用概率方法求得作用分项系数的优化计算结果为γG=1.05，γQ=1.05～1.30， 参见表2。 根据优化计算结果，同时适当考虑工程经验，DL/T 5057—1996采用了如表2所示的作用分项系数取值。

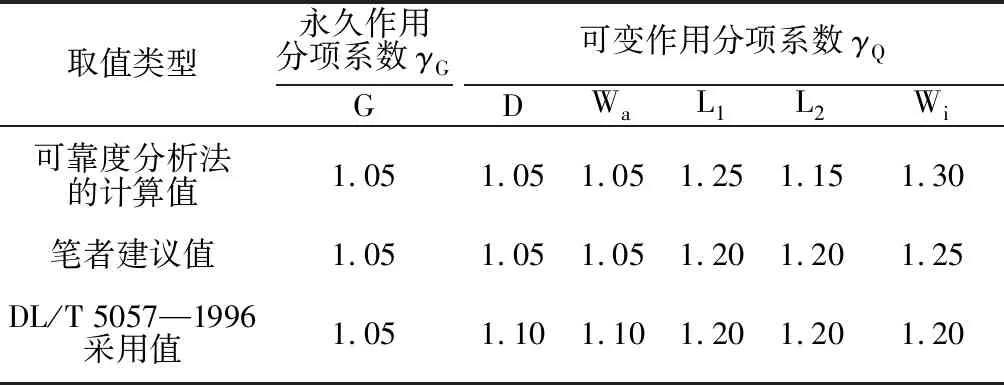
表2 作用分项系数的优化计算结果Table 2 Optimized results of acting partial coefficients

注：G为永久作用；D为吊车竖向轮压；Wa为静水压力；L1为楼面堆放可变荷载；L2为办公楼楼面可变荷载；Wi为风荷载。

表3 按“工程经验校准法”和“可靠度分析法”确定的结构系数Table 3 Structural coefficients determined by the engineering empirical calibration method andthe reliability analysis method

3.3 水工结构设计标准结构系数的确定原则与方法

水工结构设计标准分项系数设计表达式中的结构系数γd是采用概率极限状态设计法时，为达到承载能力极限状态所规定的目标可靠指标βt而设置的分项系数。γd主要是用来涵盖下列不定性因素：荷载效应计算模式的不定性；结构构件抗力计算模式的不定性；荷载、材料性能分项系数等未能完全反映的其他各种变异性。

水工结构设计标准分项系数设计表达式中的结构系数可采用按工程经验校准与按可靠度分析相结合的方法确定[2，56-57，60-61，69，71-72]。

按“工程经验校准法”确定结构系数的要点是：根据各基本变量变异性的大小，事先选定合适的荷载及材料性能等分项系数，按照分项系数设计表达式的相当安全系数与已选定的安全系数相等的原则，推求分项系数设计表达式中的最后一个分项系数γd。

按“可靠度分析法”确定结构系数的要点是：根据可靠度校准分析所确定的目标可靠指标βt和各基本变量变异性的大小，事先选定合适的荷载及材料性能等分项系数，然后用概率方法(一次可靠度分析法)经优化计算并适当考虑工程经验，确定分项系数设计表达式中的最后一个分项系数γd。

在综合分析2种方法确定的结构系数取值的基础上，按照标准修订前后的安全度设置水平不致波动过大和实用方便的原则，经适当的归并与取整后，确定水工结构设计标准最优的结构系数取值。

下面以水工混凝土结构设计规范为例，介绍水工混凝土结构设计规范分项系数设计表达式中的结构系数的确定原则与方法。

按“工程经验校准法”确定结构系数时，根据各基本变量变异性的大小，事先选定合适的荷载分项系数γG,γQ(见表2)及材料性能分项系数γc,γs，按照分项系数设计表达式的相当安全系数与SDJ 20—78规范规定的单一安全系数相等的原则，推求分项系数设计表达式中的最后一个分项系数，即结构系数γd。

按“可靠度分析法”确定结构系数时，与按“工程经验校准法”确定结构系数时一样，计算结构系数时同样选择了水工混凝土结构常用的7种典型构件，并考虑了5种不同材料组合和5种不同作用组合及若干个不同作用效应比值的影响；在计算过程中，还利用最小二乘法的原理进行了优化计算。最后取不同材料组合与不同作用组合及不同ρ值下的结构系数的加权平均值，作为该构件最优的结构系数[56-61]，按“可靠度分析法”确定的结构系数见表3。

由表3可以看出，按2种方法确定的结构系数取值是相近的，在综合分析2种方法确定的结构系数取值的基础上，按照规范修订前后的安全度设置水平不致波动过大和实用方便的原则，对最后所得结构系数进行了适当的归并与调整，DL/T 5057—1996采用的结构系数取值见表3。

4 国内外结构设计标准安全度设置水平的比较

4.1 分项系数设计表达式的相当安全系数的概念

在研究和比较国内外同类结构设计标准的安全度设置水平时，国内有的研究者往往只单纯地比较作用分项系数或材料性能分项系数取值的差异，而未考虑作用分项系数和材料性能分项系数的综合影响及抗力计算模式等的差别，因而难以得出令人信服的中外规范安全度设置水平差异的定量数据。

笔者认为，在与国外同类标准的安全度设置水平进行比较时，合理的做法应该是从结构的失效概率或可靠指标来进行比较，至少应该用分项系数设计表达式的相当安全系数来进行比较。分项系数设计表达式的相当安全系数的概念，系笔者当年在国内首次提出，详请参阅文献[78]—文献[80]。

采用分项系数设计表达式以后，分项系数与相当安全系数之间是相互关联，可以相互转化的。不论是哪一种结构构件，也不论是哪一种作用组合，经过简单的数学推演，都可以方便地建立分项系数与相当安全系数之间的联系。现举例如下。

设承载能力极限状态的分项系数设计表达式为

(1)

当仅考虑永久作用与一种可变作用的简单组合情况时,作用组合的效应设计值S可写为

S=γ0ψγd(γGSGk+γQSQk)=KSSk。

(2)

其中：

(3)

Sk=SGk+SQk；

(4)

(5)

对于混凝土结构，结构抗力设计值R可写为

(6)

其中：

(7)

Rk=Rck+Rsk；

(8)

(9)

于是，式(6)可写为：

KSSk≤KRRk；

(10)

KSk≤Rk；

(11)

K=KS/KR。

(12)

式中：KS为综合作用系数；Sk,SGk,SQk分别为作用组合的效应标准值和永久作用效应标准值及可变作用效应标准值；KR为综合考虑材料性能分项系数γc,γs和抗力计算模式系数αc,αs影响的综合抗力系数；Rk为按材料强度标准值求得的综合抗力标准值；Rck,Rsk分别为混凝土抗力标准值及钢筋抗力标准值；K为相当安全系数或综合安全系数。

由此可见，分项系数与单一安全系数之间是相互关联，可以相互转化的。不论是哪一种结构构件，也不论是哪一种作用组合，经过简单的数学推演，都可以方便地建立分项系数与相当安全系数之间的联系。

4.2 国内外结构设计标准安全度设置水平比较时应遵循的基本原则

利用相当安全系数的概念进行国内外结构设计标准安全度设置水平的比较时应遵循的基本原则为：

(1)应保证比较的起点一致，如材料强度标准值和荷载标准值的取值等。

(2)一般以中国标准的设计表达式为基准，对国外规范的设计表达式做必要的换算。例如，将国外标准设计表达式的两边分别同乘以中国标准的作用效应设计值和抗力设计值，以便考虑中外标准在作用标准值和材料强度标准值及其分项系数的取值以及抗力计算模式等方面的差异。例如，中外标准的作用分项系数和材料性能分项系数取值是不同的；在作用效应方面，中外标准风载标准值的取值原则也是不同的；在抗力方面，如为混凝土结构，中外标准混凝土强度等级的确定原则也是不同的，表现为中国标准是以150 mm立方体试件作为标准试件，而国外标准一般以150 mm圆柱体试件作为标准试件。在比较中外标准的安全度设置水平时，为了保证比较的起点一致，就应进行必要的换算。

设以下标C代表中国标准，下标F代表国外标准，下面分别给出中外标准相当安全系数的计算公式。

中国标准：

SC≤RC；

(13)

SC=γCGSCGk+γCQSCQk=KCSSCk；

(14)

(15)

SCk=SCGk+SCQk；

(16)

ρQ=SCQk/SCGk；

(17)

RC=KCRRck。

(18)

根据以上推导，式(13)可写成：

KCSSck≤KCRRck；

(19)

KCSck≤Rck；

(20)

KC=KCS/KCR。

(21)

式中：SC为中国标准作用组合的效应设计值；RC为中国标准结构抗力的设计值；KC为中国标准的相当安全系数。

国外标准：

SF≤RF；

(22)

(23)

αsKCSSck≤αRKCRRck；

(24)

(25)

(26)

(27)

或写成：

KFSck≤Rck；

(28)

(29)

式中：SF为国外标准作用组合的效应设计值；RF为国外标准结构抗力的设计值；KF为国外标准的相当安全系数。

中外结构设计标准的安全度设置水平比较时，可按式(30)求得中国标准与国外标准相当安全系数的差值百分比。

(30)

利用相当安全系数的概念，按照本文提出的上述公式进行国内外结构设计标准安全度设置水平的比较时，既保证了比较的起点一致，同时也比较方便地考虑了中外标准在荷载标准值和材料强度标准值及其分项系数的取值以及抗力计算模式等方面的差异。

5 结 论

(1)基于结构可靠度理论的概率极限状态设计原则在水工结构设计标准中得到了越来越广泛的应用，形成了一股强劲的发展势头，建议在我国的水工结构设计标准中继续积极稳妥地推广应用基于结构可靠度理论的概率极限状态设计原则。

(2)关于“校准法”，可以有2种方式：一种是以现行标准为基准，用概率方法(一次可靠度分析法)反算出现行结构设计标准中隐含的可靠指标β，摸清现行标准结构设计的总体安全度设置水平，并据此确定新标准拟采用的目标可靠指标；另一种是以现行标准的分项系数设计表达式及相应的分项系数取值方案为基础，求出各种构件相应于分项系数设计表达式的相当安全系数，进而确定新标准拟采用的相当安全系数(或称“安全度设置水平”)。在可靠度校准分析或推求相当安全系数的过程中，还可以发现现行标准中个别构件的安全度设置水平过高或过低的不合理情况，作为标准修订时对构件的安全度设置水平进行局部调整的依据。

(3)水工结构设计标准的作用分项系数，是在按超载系数的概念确定的作用分项系数取值的基础上，采用概率方法经优化计算并适当考虑工程经验优选确定的。

(4)水工结构设计标准分项系数设计表达式中的结构系数可采用按工程经验校准与按可靠度分析相结合的方法确定，在综合分析2种方法确定结构系数取值的基础上，按照标准修订前后的安全度设置水平不致波动过大和实用方便的原则，经适当的归并与取整后，确定水工结构设计标准最优结构系数取值。

(5)分项系数与单一安全系数之间是相互关联、可以相互转化的。不论是哪一种结构构件，也不论是哪一种作用组合，经过简单的数学推演，都可以方便地建立分项系数与相当安全系数之间的联系。

(6)在与国外同类规范的安全度设置水平进行比较时，合理的做法应该是从结构的失效概率或可靠指标来进行比较，至少应该用分项系数设计表达式的相当安全系数来进行比较。利用相当安全系数的概念，文中还给出了中外结构设计标准的安全度设置水平比较时应遵循的基本原则和方法。