肘杆式伺服压力机运动学仿真与工艺轨迹规划

周 洋，叶春生，莫健华

（华中科技大学 材料成形及模具技术国家重点实验室，湖北 武汉 430074）

肘杆式伺服压力机运动学仿真与工艺轨迹规划

周 洋，叶春生，莫健华

（华中科技大学 材料成形及模具技术国家重点实验室，湖北 武汉 430074）

基于肘杆式压力机的基本结构，进行运动学逆解分析。提出一种参数化组合式正弦函数作为加速度曲线的加减速算法，规划滑块的运动轨迹，使滑块的运动轨迹更加平滑，提高了伺服压力机高速工作时平稳性，降低了对伺服控制系统瞬态响应的要求。利用Matlab平台搭建肘杆式压力机的运动学模型，由给定的滑块运动轨迹曲线，仿真得到精确的曲柄角位移、角速度和角加速度曲线，可作为伺服电机控制的输入量，为伺服压力机的控制提供重要依据，为其他伺服压力机传动机构的分析和控制提供一种可行的方法。

机械设计；肘杆机构；伺服压力机；Matlab/Simulink；运动学仿真；工艺轨迹规划

近年来，随着伺服控制技术的飞速发展，伺服控制系统已经广泛应用于材料加工的各个领域。伺服压力机经过近十几年的快速发展，已大有取代传统机械压力机的趋势。其主要优势体现在高效性、高精度、高柔性、低噪声、节能环保等方面[1][2]。伺服压力机的技术关键在于伺服电机的控制技术，主要体现在电机输出功率的控制和滑块运动轨迹曲线的控制。一般而言，只对输入的运动轨迹进行单段处理，使得每个运行段都有零速度、加速、匀速、减速、零速的过程，这样大大影响伺服压力机的加工效率，同时频繁剧烈的加减速会加剧机床的磨损，影响使用寿命[3]。本文根据不同的工艺要求，在不同的加工段采用S形加速度曲线，使得速度和位移曲线在多个加工段之间平滑过渡，形成连续平滑柔性高的成形曲线，系统运行更平滑，减小了瞬时冲击和噪声，改善了工作环境，降低了对伺服系统瞬时响应的要求。借助Matlab/Simulink强大的建模仿真能力，建立肘杆式伺服压力机的运动学模型，得到曲柄的角位移、角速度和角加速度曲线，改善对伺服电机的控制，从而提高伺服肘杆式伺服压力机的工作性能。

1 肘杆式传动机构

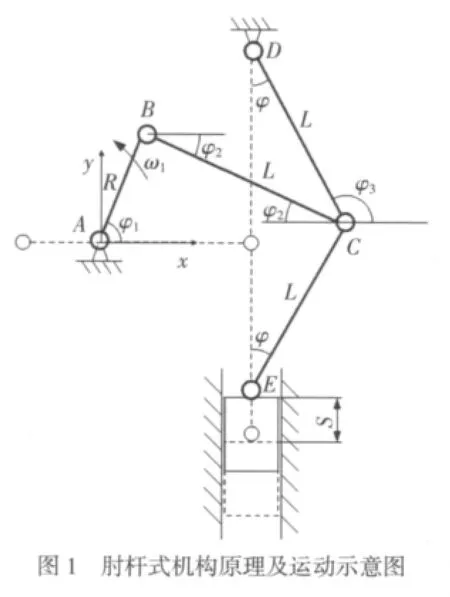
肘杆式伺服压力机是一种多连杆传动的压力机，具有较好的急回特性和一定的增力作用，在工作区域有较为理想的速度特性，是现代伺服压力机中一种常见的传动形式。本文以肘杆式压力机为研究对象，如图1所示为直线连杆肘杆式传动机构结构原理图，其中曲柄AB驱动等边连杆BC、CD和CE带动定向滑块做直线往复运动。

2 运动学逆解分析

机构的运动分析就是根据原动件的运动规律，求解从动件的运动规律。其方法主要有图解法、解析法和实验法等。本文采用解析法对肘杆式机构进行运动学分析，解析法基本原理是在机构已知参数和应求未知量之间建立数学模型，然后对数学模型进行求解，从而获得精确的计算结果。

如图1所示，AB杆为驱动杆，可以绕A点做圆周运动，D点为铰接固定点，在AB杆的驱动下，DC杆绕D点摆动，E点为铰接点，CE杆带动滑块做定向往复运动。设AB杆的杆长为R，转动角位移为φ1，角速度为 ω1，BC 杆、CD 杆和 CE 杆杆长为 L，DC杆摆动角位移为φ，DC杆的摆动角速度为ω，BC杆的水平夹角为φ2，滑块的位移为S。

以A点为圆心，建立如图2所示的坐标系。已知滑块 E 点位置（xe，ye）、速度 v、加速度 a、曲柄 AB杆长R、连杆BC、CD、CE杆长L，求解曲柄AB的角位移φ1、角速度ω1和角加速度a1。

2.1 位置分析

由图1可知，E点的位置坐标为：

其中，y¨e为滑块加速度，α为CD杆绕D点摆动的角加速度，α2为BC杆相对于C点的转动角加速度。

3 伺服压力机运动轨迹的规划

在高速加工中，由于伺服压力机的运动部件滑块具有较大的惯性，机床在启动、停止及速度变化时容易产生冲击、失步、超调或震荡；同时当程序轨迹不平滑时，机床频繁加减速，使加工速度难以提高，并影响到零件表面的加工精度。为提高加工质量，必须进行适当的加减速控制和运动轨迹优化。

在伺服压力机规划工艺轨迹和控制时,滑块的位移曲线作为整个伺服系统的输入,需要柔顺平滑同时能用简单的函数表达式表示,而且工艺曲线的函数表达式要至少二阶可导。然而并非任意曲线都能用简单的二阶可导的函数表达式来表示,因而大大限制了伺服压力机的加工工艺设计和控制。S形曲线加减速的动力学特性较好，本文在S形加减速曲线的基础上，采用参数化组合式正弦函数作为加速度曲线的加减速算法，将任意工艺曲线分成多段组合正弦函数,使整段工艺曲线二阶可导且柔顺平滑，提高了伺服压力机的工作性能，降低了伺服系统的动态响应要求,同时在一定程度上也降低了控制难度。

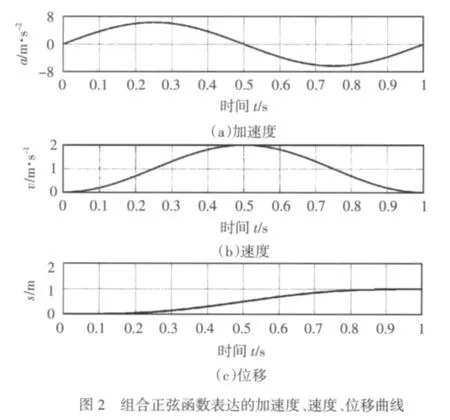
令 s（τ）=1 可求得 A=2π，此时加速度、速度、位移曲线如图2a、b、c所示。

将 s（τ）作为自变量，则可以用多段 s（τ）描述伺服压力机中电机、曲柄以及滑块在工作周期内的运动曲线，以曲柄转角为例子，每段加减运动曲线可以表达为：

其中，θi和θF分别表示电机的起始角位移和终止角位移。

4 建模仿真

4.1 伺服压力机的运动模式

伺服压力机的典型工作循环包括如下几个过程：

（1）滑块空行程高速向下运动。根据加工工艺要求，滑块在伺服电机的驱动下，从上死点开始以设定的速度和加速度运动到特定的位置。在冲头接触工件之前，不需要关心滑块是如何运行，只在意接触工件的时候冲头是否能保持工艺要求的速度或者满足冲头到达某点的实际位置，因此滑块一般都以比较高的速度向下运动，从而减少设备空行程的时间，提高生产效率。

（2）滑块工作行程慢速向下运动。根据加工工艺要求，滑块可以比较慢的速度向下运动而进行加工工作，还可以在下死点或下死点附近停留一定的时间，或者两种方式相结合，从而大大提高设备的加工精度和工艺适应性。

（3）滑块空行程高速向上运动。当滑块运动到下死点，待加工工作完成以后，滑块以设定的速度和加速度从下死点高速运动到上死点。

不同的锻压工艺对滑块的运动规律有不同要求。伺服压力机典型的加工模式有：减噪模式和整形模式。

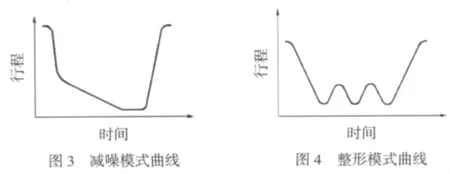
减噪模式是滑块首先快速下行到工作点，然后再慢速下压，并在极限工作位置上停留一段时间，然后再快速回程。这种模式广泛用于冷锻和弯曲工艺中。如图3所示。整形运动模式则是滑块振动压制，最后快速回程。这种运动模式提高了成形件的精度，改善了产品质量，特别适合那些难成形材料的深拉延工作。如图4所示。4.2 肘杆式伺服压力机运动学的Simulink仿真

Matlab语言是由美国Mathworks公司开发的集科学计算、数据可视化和程序设计为一体的工程应用软件，现已成为工程学科计算机辅助分析、设计、仿真以至教学等不可缺少的基础软件。Simulink是Matlab中的一种可视化仿真工具，是一种基于Matlab的框图设计环境，是实现动态系统建模、仿真和分析的一个软件包，被广泛应用于线性系统、非线性系统的建模和仿真中。

本文借助Matlab/Simulink强大的建模仿真能力，建立肘杆式伺服压力机的运动学模型，做出滑块在减噪模式和整形模式下的位移曲线，根据肘杆式机构的运动学加速度方程和初始条件，令R=100mm，L=700mm，建立Simulink仿真模型如图5所示，其中将滑块位移S作为输入，曲柄AB的瞬时位置、角速度和角加速度作为输出，并存储在工作空间simout1中，Out1模块中是定义的滑块的位移曲线，经过微分得到速度曲线和加速度曲线，作为定义的acceleration（u）函数的输入量，acceleration（u）函数的直接输出量为曲柄AB的加速度α1，经过积分模块得到其角速度ω1和角位移φ1。

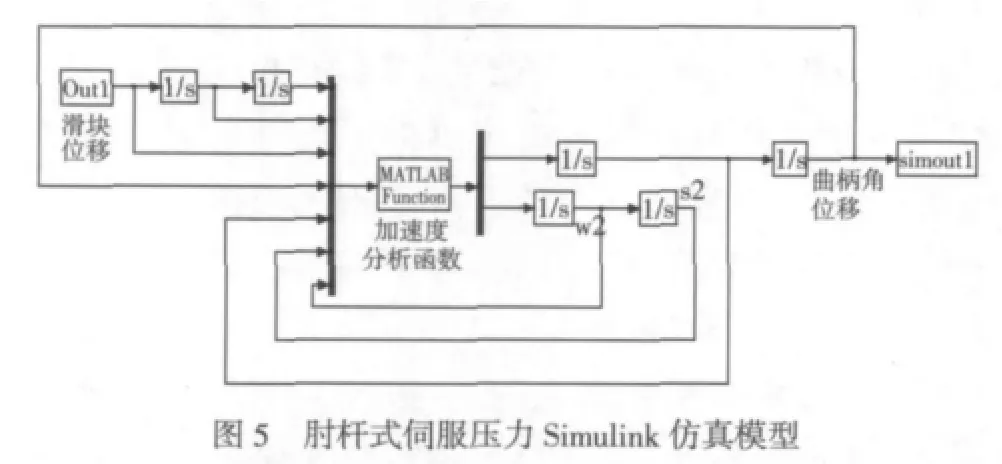
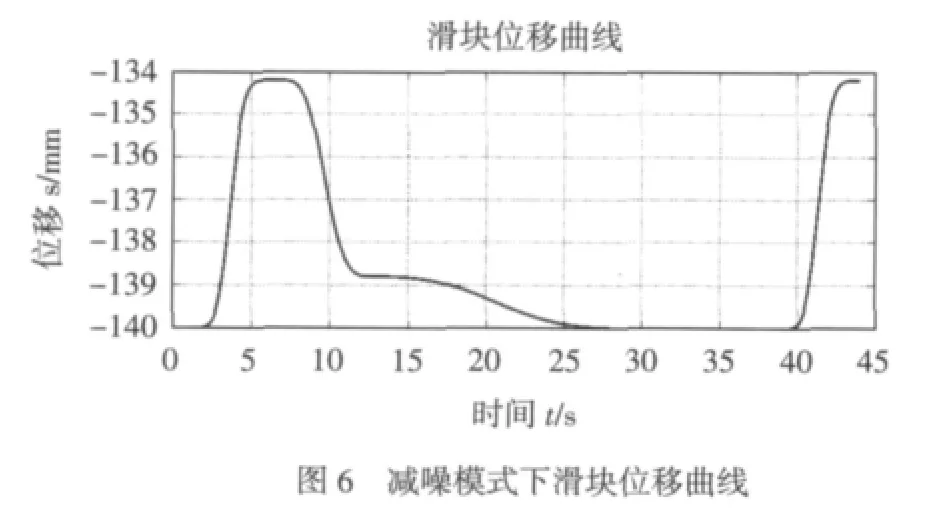
在Matlab/Simulink中，Out1模块（图5）的输入曲线作为一组输入信号需要能够用参数化方程来表示。根据组合式正弦函数作为加速度曲线的加减速算法，对于任意工艺曲线都可由多段组合式正弦函数来表示，因此在减噪模式下令T1=12πs，在整形模式下令T2=14πs，滑块初始位置在下死点，做出滑块在减噪模式和整形模式下的位移曲线如图6、图7所示。图中曲线的参数化表达式将作为输入信号导入Out1模块中进行仿真实验。

4.3 仿真及结果分析

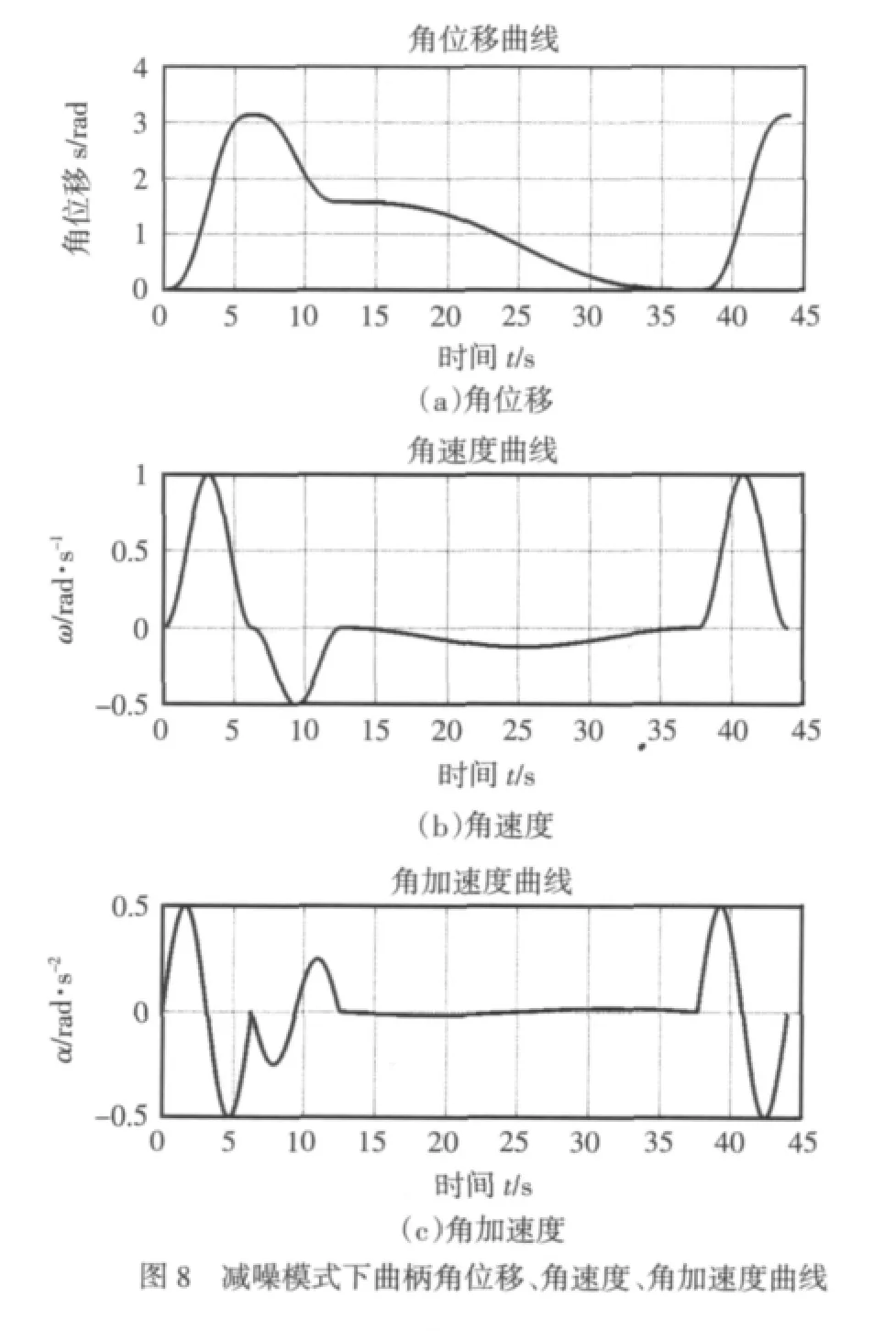
减噪模式仿真结果如图8a、b、c所示。

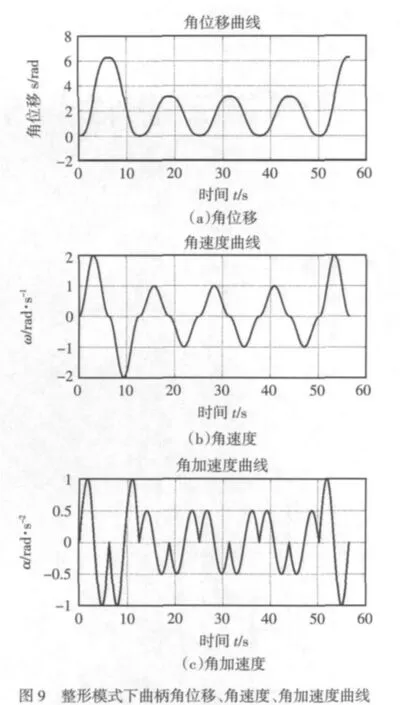
整形模式仿真结果如图9a、b、c所示。

由以上仿真结果可知，在组合式正弦函数加速度曲线的加减速算法下，滑块和曲柄的位移曲线平滑，使得压力机工作平稳，噪声低，耗能少，能够满足冲压工艺要求，且对伺服电机的瞬态响应要求低，精确的曲柄角速度和角加速度曲线能够作为伺服控制系统的输入曲线，能够大大改善伺服控制系统，减小滑块的实际位移曲线与工艺要求曲线的误差，从而增加伺服控制系统的控制精度。

5 小结

本文以肘杆式伺服压力机为研究对象，采用解析法对肘杆式压力机进行了运动学分析，提出用参数化组合式正弦函数作为加速度曲线的加减速算法，规划伺服压力机滑块的运动轨迹，使其运动曲线更加平滑，柔性更好，减小了冲击噪声，降低了对伺服系统瞬时响应的要求，为各种工艺轨迹的规划提供了一种可行的方法。借用Matlab/Simulink强大的建模仿真能力，建立肘杆式伺服压力机的运动学模型，根据各种工艺要求将滑块的运动曲线作为输入，逆向仿真得到曲柄的运动角位移、角速度和角加速度曲线，为伺服压力机的控制提供了重要依据，为伺服压力机控制系统的改善提供了较大助力。

[1] 叶春生，侯文杰，张军伟，等.数字伺服压力机控制系统的研究[J].锻压技术，2009，34（6）：117-122.

[2] 叶春生，莫建华，樊自田，等.曲柄连杆伺服压力机控制模型的研究及系统实现[J].锻压装备与制造技术，2009，（5）：53.

[3] 张得礼，胡育文.伺服压力机加工运动的控制[J].装备，2010.

[4] 赵升吨，张志远，何予鹏，等.机械压力机交流伺服电动机直接驱动方式合理性探讨.锻压装备与制造技术，2004，41（6）：19-23.

[5] 黄永安，马 路，刘慧敏.MATLAB7.0Simulink6.0建模仿真开发与高级工程应用[M].北京：清华大学出版社，2005.

[6] 孙友松，周先辉，黎 勉，等.交流伺服压力机及其关键技术[J].锻压技术，2008，（4）：1-8.

[7] 何德誉.曲柄压力机[M].北京：机械工业出版社，1981.

[8] 杨 平，马瑞娜，张云安.基于MATLAB永磁同步电机控制系统建模仿其方法[J].沈阳工业大学学报，2005，（4）：195-199.

[9] 王成元.矢量控制交流伺服驱动电动机[M].北京：机械工业出版社，1994.

[10] 李永东.交流电机数字控制系统[M].北京：机械工业出版社，2002.

[11] 李 峰.基于DSP的SVPWM调制技术的研究[J].电气传动自动化，2005，（4）：1-5.

Kinematics simulation and design of technological trajectories of toggle servo press

ZHOU Yang,YE Chunsheng,MO Jianhua
（State Key Laboratory of Material Process and Die and Mould Technology,Huazhong University of Science and Technology,Wuhan 430074,Hubei China）

Based on the basic structure of toggle servo press,inverse kinematics analysis has been carried out in the text.A kind of combined sine function has been presented as an algorithm for acceleration curve.Technological trajectories designed by this algorithm are smoother,which can improve the stability of the servo press in high speed.Kinematics model of servo press has been established by use of Matlab software.The trajectory curve of slipper has been input in kinematics model and the simulated angular displacement curve,angular speed curve and angular acceleration curve of the crank have been obtained.It provides a feasible method of analysis and control for servo press with other transmission mechanisms.

Toggle rod mechanism;Servo press;Matlab/Simulink;Kinematics simulation;Technological trajectories

TG315.5

B

1672－0121（2012）03－0037－05

2011-12-15

周 洋（1986-），男，硕士在读，主攻伺服压力机设计研究