旋波近似下的量子Zeno效应时间

李兴敏，宋立军

(1.长春理工大学 理学院，长春 130022;2.长春大学 理学院，长春 130022)

旋波近似下的量子Zeno效应时间

李兴敏1，宋立军2

(1.长春理工大学 理学院，长春 130022;2.长春大学 理学院，长春 130022)

频繁对系统进行量子测量会产生阻抑不稳定量子态衰减的量子Zeno效应。通过对哈密顿量以及不稳定量子态进行中岛变换，在薛定谔绘景下直接计算出量子Zeno效应时间，得出弱耦合情况下发生量子Zeno效应所需的最基本条件，给出量子Zeno效应时间与测量光场频率、耦合强度及不稳定量子态自身能级间隔之间的关系。

量子Zeno效应;中岛变换;旋波近似

0 引言

古希腊哲学家Zeno曾提出著名的“Zeno佯谬”——“阿基里斯追不上乌龟”，这是一个有趣的哲学问题。Zeno论证到，当飞毛腿阿基里斯从后面追赶乌龟的时候总是要到达他起步时乌龟所在的位置，当他到达乌龟所在位置时，乌龟又前进了一段距离，如此下去，阿基里斯是追不上乌龟的。Misra和Sudarshan根据Zeno佯谬提出频繁测量不稳定量子态会阻抑其衰减速率，也就是量子尺度下的Zeno效应——量子Zeno效应(Quantum Zeno Effect，简称QZE)［1］，这一效应为量子光学和量子信息的发展产生了极大影响，同时也促进了量子测量理论的发展。

量子Zeno效应的提出，使人们在研究不稳定量子态衰减时有了重要理论依据。在研究量子态保持［2］以及保护纠缠态［3］等方面，运用量子Zeno效应理论取得了一系列重要成果。2001年，人们在研究失谐冷原子囚禁［4］时，发现冷原子衰减速率出现明显异常，首次观察到量子Zeno效应出现，但是这观测到的量子Zeno效应还不能够实现人为操控。

人为控制量子态衰减能否在实验上取得成功，很大程度上依赖于量子Zeno效应时间，所以有关量子Zeno效应时间研究越来越引起人们广泛关注。在二能级系统中，理论研究已经给出了相互作用绘景中氢原子在旋波近似和非旋波近似(弱耦合情况)下的量子Zeno效应时间［5，6］，然而这两种量子Zeno效应时间的计算方法都需要进行绘景变换，并不是十分方便与直接。本文通过对哈密顿量和量子态进行幺正变换［7］，取得有效哈密顿量和有效量子态，进而给出在薛定谔绘景中旋波近似条件下量子Zeno效应时间计算的方法，并给出了量子Zeno效应时间与各个参量之间的离散数值关系，该方法具有一定普适性，丰富了量子Zeno效应时间计算方法，对于指导弱耦合情况实现人为控制量子态衰减速率具有重要意义。

1 二能级系统

在量子光学二能级系统中，如果原子与辐射场之间耦合强度很小，通常考虑旋波近似，采用Jaynes－Cummings(J－C)模型［8］来描述原子与辐射场之间的相互作用。在本文中，我们考虑弱耦合情况，并且采用JC模型来描述哈密顿量(h=1)。

经过时间t后，直接计算量子态仍处于原状态的概率需要进行绘景转换，比直接在薛定谔绘景中计算繁琐了很多。此处，我们对哈密顿量进行一次幺正变换e－s——中岛变换，得到有效哈密顿量，从而简化计算。这里，我们取

经过幺正变换后的有效哈密顿量为Heff=e－SHeS，展开为

计算发现在式(6)中有

考虑到对哈密顿量进行了幺正变换(中岛变换)，那么对所选择的初态|e，{0})也要进行相应的演化，

(8)式和(9)式分别为经过幺正变换后的有效哈密顿量和有效初态，从有效哈密顿量方程(8)中，可以发现当有效哈密顿量作用在量子态上，无需通过绘景变化可直接得出其所对应的能量表达式，即可直接在薛定谔绘景中直接计算。在(9)式中，同前面哈密顿量的幺正变换一样，也只对其取到二阶量。

2 量子Zeno效应时间

如果对一个量子态进行短时测量，那么在测量间隔t时间内不衰减的概率可以用表达式［5］

来表示。如果在同t时间内进行n倍次测量，即测量间隔变成t，此时量子态不衰减的概率为n

当n→∞时，

从式(12.b)可以看出，测量频率跟量子态的存在概率成指数关系。当对量子态进行频繁测量时，量子态的衰减概率大大降低，如果进行连续性测量(即n→∞)，量子态处于不衰减状态，量子Zeno效应发生。在本文中，称 τz为量子 Zeno 效应时间［5］。

将经过幺正变换后的有效初态|ψ0〉=e－S|e，{0}〉和有效哈密顿量H=Heff，分别带入方程(11)，略去高阶小量，可以得到

通过(13)－(16)式计算，得到了哈密顿量差值的平方(ΔH)，也就是量子Zeno效应时间τz的负二次方，对(ΔH)2取倒数并且开平方，能够得到薛定谔绘景中的量子Zeno效应时间为

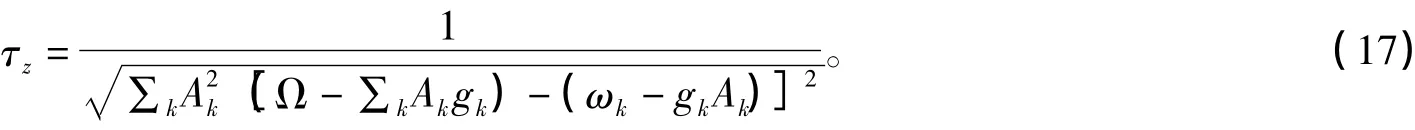
从(17)式可以看出，量子Zeno效应时间τz跟原子自身能级间隔Ω、测量光场频率ωk以及耦合强度gk是紧密相关的。因此，要想实验上实现观察弱耦合情况可控量子Zeno效应，必须考虑到上述三个参量，并且遵循方程(17)。

3 总结

本文研究了弱耦合情况下，在J－C模型中利用对哈密顿量和不稳定量子态进行幺正变换(中岛变换)，实现了薛定谔绘景中直接计算量子Zeno效应时间的计算方法，发现量子Zeno效应时间跟原子自身能级间隔Ω、测量光场频率ωk以及耦合强度gk之间的密切关系，计算结果对将来实验上弱耦合情况实现量子态保持以及保护纠缠态等具有重要意义。

［1］ B Misra，E C G Sudarshan.The Zeno＇s paradox in quantum theory［J］.J.Math.Phys，1977(18):756.

［2］ D Dhar，L K Grover，S M Roy.Preserving Quantum States using Inverting Pulses:A Super－Zeno Effect［J］.Phys.Rev.Lett，2006(96):100405.

［3］ Sabrina Maniscalco，Francesco Francica，Rosa L.Zaffino，Nicola Lo Gullo，Francesco Plastina，Protecting Entanglement via the Quantum Zeno Effect［J］.Phys.Rev.Lett，2008(100):090503.

［4］ M C Fischer，B Gutiérrez－Medina，M G Raizen.Observation of the Quantum Zeno and Anti－Zeno Effects in an Unstable System［J］.Phys.Rev.Lett，2001(87):040402.

［5］ P Facchi，S Pascazio.Temporal behavior and quantum Zeno time of an excited state of the hydrogen atom［J］.Phys.Lett.A，1998(241):139－144.

［6］ H Zheng，S Y Zhu，M S Zubairy.Quantum Zeno and Anti－Zeno Effects:Without the Rotating－Wave Approximation［J］.Phys.Rev.Lett，2008(101):200404.

［7］ David Zueco，Georg M Reuther，Sigmund Kohler，Peter Hänggi.Qubit－oscillator dynamics in the dispersive regime:Analytical theory beyond the rotating－wave approximation［J］.Phys.Rew.A，2009(80):033846.

［8］ E T Jaynes，F W Cummings.Comparison of quantum and semiclassical radiation theories with application to the beam maser［J］.Proc.IEEE，1963(51):89.

Study on Quantum Zeno Effect Time with Rotating-wave Approximation

LI Xing－min1，SONG Li－jun2

(1.School of Science，Changchun University of Science and Technology，Changchun 130022，China;2.College of Science，Changchun University，Changchun 130022，China)

The unstable quantum states can be prevented from decay when measurements are frequently applied to the system，which is called quantum Zeno effect.Through Nakajima transformation on Hamiltonian and unstable quantum states，this article presents a method to compute the quantum Zeno effect time in Schrodinger picture，gets the basic condition of quantum Zeno effect in weak coupling and gives the relations between quantum Zeno effect time and the frequency of measuring optical field，the coupling strength and the energy－level spacing.

quantum Zeno effect;Nakajima transformation;rotating－wave approximation

O431.2

A

1009－3907(2012)08－0960－03

2012－05－30

教育部科学技术研究重点项目(211040);吉林省自然科学基金项目(20101514);吉林省青年基金项目(201201140);吉林省教育厅科学技术研究基金项目(2012245)

李兴敏(1986－)，男，山东青岛人，硕士研究生，主要从事理论物理研究;宋立军(1971－)，男，吉林东丰人，教授，博士，主要从事量子信息、量子光学和凝聚态物理的研究。

责任编辑:程艳艳