位势场与涡轮端区二次流的相互作用机理研究

綦 蕾，邹正平，刘火星，王 雷

（1.北京航空航天大学 航空发动机气动热力国防科技重点实验室，航空发动机数值仿真研究中心，北京 100191；2.中航工业沈阳发动机设计研究所涡轮室，辽宁 沈阳 110015）

0 引 言

随着涡轮气动负荷的不断提高，小展弦比涡轮叶片设计技术得到越来越多的应用［1］，特别是在高压涡轮和中压涡轮等的设计中。对于小展弦比涡轮叶片而言，端区损失（包括端区二次流损失和叶尖泄漏流损失）是其气动损失的主要来源，占总损失的百分比甚至达到60%～70%［2］。因此，如何在设计中有效组织涡轮内部流动，控制涡轮端区流动损失的产生成为小展弦比高负荷涡轮设计中的关键。

国内外已有大量针对涡轮端区流动的研究，并获得了定常情况下的端区流动特性和旋涡模型［3－5］，其中Sieverding［6］和 Langston［7］对有关涡轮二次流动的研究进行了较全面的回顾与总结。然而，涡轮内部的流动本质上是周期性非定常的，叶片排之间的相互作用将对涡轮叶片通道内的流动产生不可忽视的影响，在亚声速涡轮中如尾迹与二次流／泄漏流、位势作用与二次流／泄漏流等。这些因素对涡轮性能的影响如何，是否应该在设计体系中明确体现，以及如何在设计体系反映这些非定常效应，目前并不十分清楚。所以，了解和利用非定常效应并将其合理体现到实际的发动机涡轮设计中去，对于进一步提高涡轮的性能具有重要的意义。

位势作用是引起涡轮内部流动非定常性的主要因素之一，它的影响可以同时向上、下游相邻叶片排传递，在其作用范围之内引起的非定常效应十分明显。Korakianitis［8］通过数值方法研究了上游静子尾迹和位势场对下游转子的非定常作用，结果显示当静子叶片数与转子叶片数之比R≈1时，静子尾迹的非定常作用占主导地位；当R＞3时，静子的位势作用占主导地位；当R取中间值时，尾迹和位势场的影响同等重要，转子对静子的影响也具有上述规律。Miller［9］等人通过实验和数值模拟研究了某高压涡轮中尾迹、激波和位势场的非定常作用，结果发现在典型设计条件下，下游导叶位势作用对转子通道中马赫数为1以后的区域影响较大。Schlienger等人［10］对某涡轮中旋涡－尾迹－叶片之间的非定常相互作用进行了实验研究，结果显示转子出口二次涡和尾迹在下游静子的位势作用影响下呈明显的非定常性，且非定常流场主要取决于转子与下游静子的相对周向位置（相位）。剑桥大学 Hodson等人［11－12］在研究尾迹与边界层相互作用的基础上，进一步通过在叶栅下游放置一排运动的大圆柱模拟下游叶片排的非定常位势作用，结果表明，下游的非定常位势作用对叶栅吸力面边界层流动有重要的影响，下游圆柱的运动导致叶栅通道中的流动周期性的加速和减速，在减速的情况下，边界层转捩提前，边界层中动量损失增大。国内北航邹正平等［13］通过数值模拟研究了单级轴流涡轮内部上游叶片排尾迹和位势作用对下游叶片表面负荷分布的影响。西工大周莉和蔡元虎［14］进行了不同轴向间距下涡轮级内非定常流场的数值研究，结果表明轴向间距对转子内流动的非定常性有着强烈影响，随着轴向间距的减小，静叶尾迹强度及影响范围增加。从已有的研究来看，虽然人们对于涡轮内部非定常位势作用已有了一定认识，但是研究过程中没有将位势作用的影响单独提炼出来进行分析，另外对位势作用的影响机理还缺乏细致的描述。因此，位势作用对涡轮端区二次流的非定常作用机理仍然有待于进一步的深入研究。

本文的主要工作是，利用数值模拟手段对已有实验结果的1.5级低展弦比、高负荷亚声速涡轮进行非定常流动研究，通过对非定常结果的详细分析，分析了下游位势作用对涡轮转子出口端区流动性能的影响，深入探讨了下游位势场对端区二次流和叶尖泄漏流的非定常作用机理。

1 算例和数值方法

1.1 算例介绍

研究对象采用已有实验结果的瑞士联邦工学院LISA 1.5级亚声速轴流涡轮。该涡轮的设计特点为高负荷、低展弦比和无冠，轮毂和机匣均为等半径设计。叶型设计模拟了内冷式高压燃气涡轮，因此叶片都具有较大的前缘半径和叶片厚度，转子叶尖间隙高度为1%叶高（0.68mm），各叶片排（下文分别简称导叶1、动叶1和导叶2）部分几何和气动参数见表1，其他参数详见文献［15］。

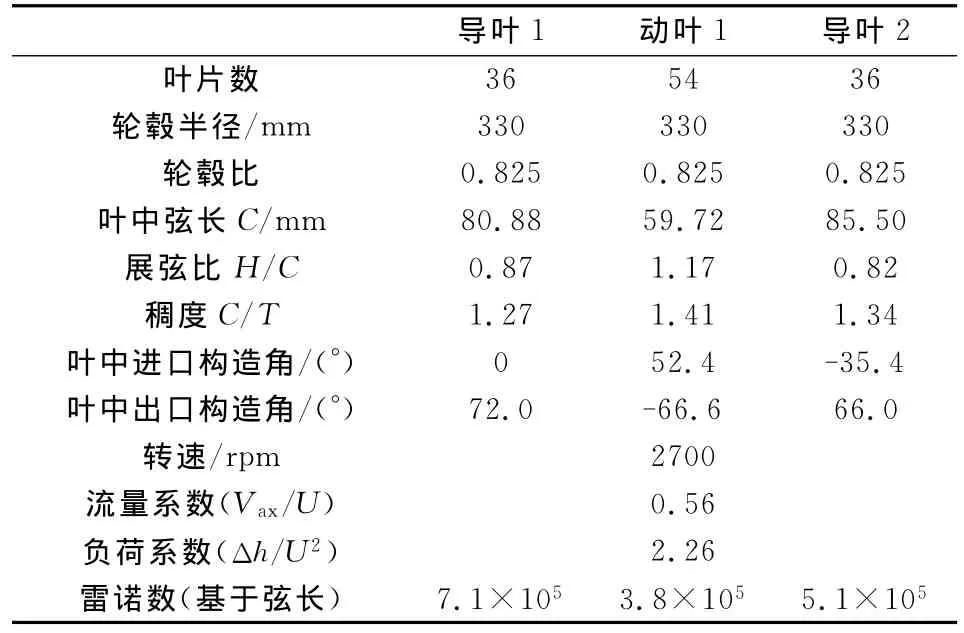
表1 LISA 1.5级轴流涡轮几何和气动参数［15］Table 1 Geometric and aerodynamic parameters of LISA 1.5－stage axial turbine

本文数值模拟工作主要包括2个方案。算例1：对1.5级涡轮进行非定常数值模拟，目的是为了与已有的实验结果进行比较，验证计算结果的可靠性。算例2：为了排除导叶1出口流场对动叶1端区流动的非定常影响，对动叶1＋导叶2两个叶片排的流场进行了非定常数值模拟。

1.2 数值方法

采用商用软件CFX求解三维定常／非定常粘性雷诺平均Navier－Stokes方程，数值方法采用时间追赶的有限体积法，空间离散采用二阶迎风格式，时间离散应用二阶后差欧拉格式，并采用多重网格技术加速收敛。湍流模型为Shear Stress Transport模型（简称SST模型）。非定常计算时将各排叶片数36∶54∶36简化为2∶3∶2，即导叶1、动叶1和导叶2分别计算2、3和2个通道。动叶排经过两个静子通道的时间为一个周期，每个周期设定60个物理时间步。

图1给出了算例1的计算网格，网格总数为3，739，305。导叶1、动叶1和导叶2的流向、径向和周向网格数分别为121×61×69、109×77×57和125×61×69，其中动叶1的叶尖间隙为蝶型网格，间隙的径向网格数为17，靠近叶尖和机匣两端分别加密。所有固壁第一根网格线的y＋值均小于2，满足湍流模型的要求。

算例2的网格总数为3，071，787，动叶1和导叶2流向、径向和周向网格数分别为125×81×57、125×61×69，其中动叶1叶尖间隙径向网格数为21。

图1 1.5级涡轮计算网格Fig.1 Computational grid of 1.5－stage turbine

进口边界条件给定总温、总压和气流角。算例1中总温为329.2K，轴向进气，总压分布根据实验测得的进口边界层分布进行了修正；出口给定截面平均静压值。算例2的边界条件通过如下方法确定：将算例1的非定常计算结果进行时间平均，取动叶1进口绝对总温、总压和气流角的周向平均值分布作为新的进口边界条件，进口边界的位置向上游延伸至距动叶前缘约1倍轴向弦长处。2个算例的进口湍流度均设为5%。交界面处理定常计算采用掺混面方法，非定常计算采用插值方法。

2 计算结果与分析

2.1 1.5级涡轮计算结果与实验结果比较

表2 给出了1.5级非定常计算结果与实验结果的总参数比较。从表中可以看出，不论是总性能参数还是各叶片排进、出口参数，计算结果与实验结果都吻合得较好。

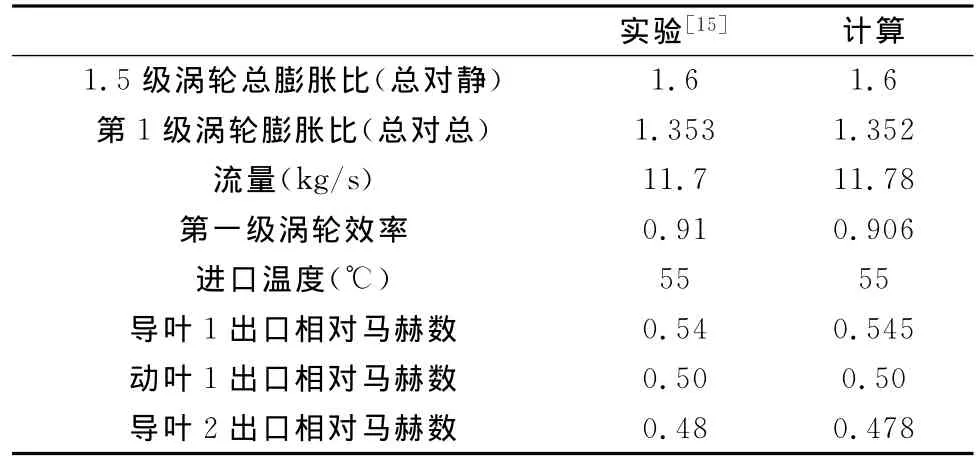
表2 计算结果与实验结果总参数比较Table 2 Comparison of total parameters between computational and experimental results

图2给出了非定常时均结果导叶1出口（距尾缘约15%叶中轴向弦长位置，下同）计算和实验的比较。图2（a）和（b）分别为计算结果和实验结果出口总压损失系数分布，图中将一个叶片通道沿径向和周向都划分为5等份。总压损失系数Cpt定义为：

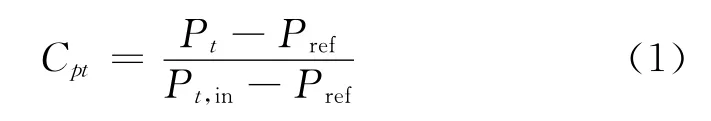
式中Pref为导叶2出口轮毂端壁处静压值，Pt，in为导叶1进口叶中总压。图中显示，计算结果与实验结果吻合较好，主流中大部分区域总压损失系数接近1。大约在40%栅距、20%～70%叶高之间均匀分布的高损失区为导叶1出口尾迹，计算结果与实验结果尾迹中心的总压损失系数值都在0.9左右。在靠近端壁10%和80%叶高附近存在明显的高损失区域，这是由轮毂和机匣通道涡产生的，核心区的总压损失系数值均小于0.8。

值得注意的是，实验结果表明90%叶高与机匣之间还存在一个高损失区，文献［15］中描述为“机匣通道涡离开叶片吸力面后，从机匣端壁处形成的新的边界层”。虽然计算结果的这一新边界层范围比实验结果小，但是从等值线分布依然可以看出新边界层的存在，定量的差别可能来自于计算时没有考虑机匣和叶片表面粗糙度以及边界层转捩等细节因素的影响，对此还需要进一步深入分析。

图2（c）为导叶1出口气流角的周向平均值分布。图中显示，计算结果与实验结果符合的较好，在80%叶高以下区域存在少量偏差，但差别小于2°。在20%～70%叶高区域气流角沿径向的变化很小，而在20%叶高以下和70%叶高以上端壁附近的流动呈现出朝端壁过转、朝叶中欠转的趋势，这是由轮毂和机匣通道涡引起的。

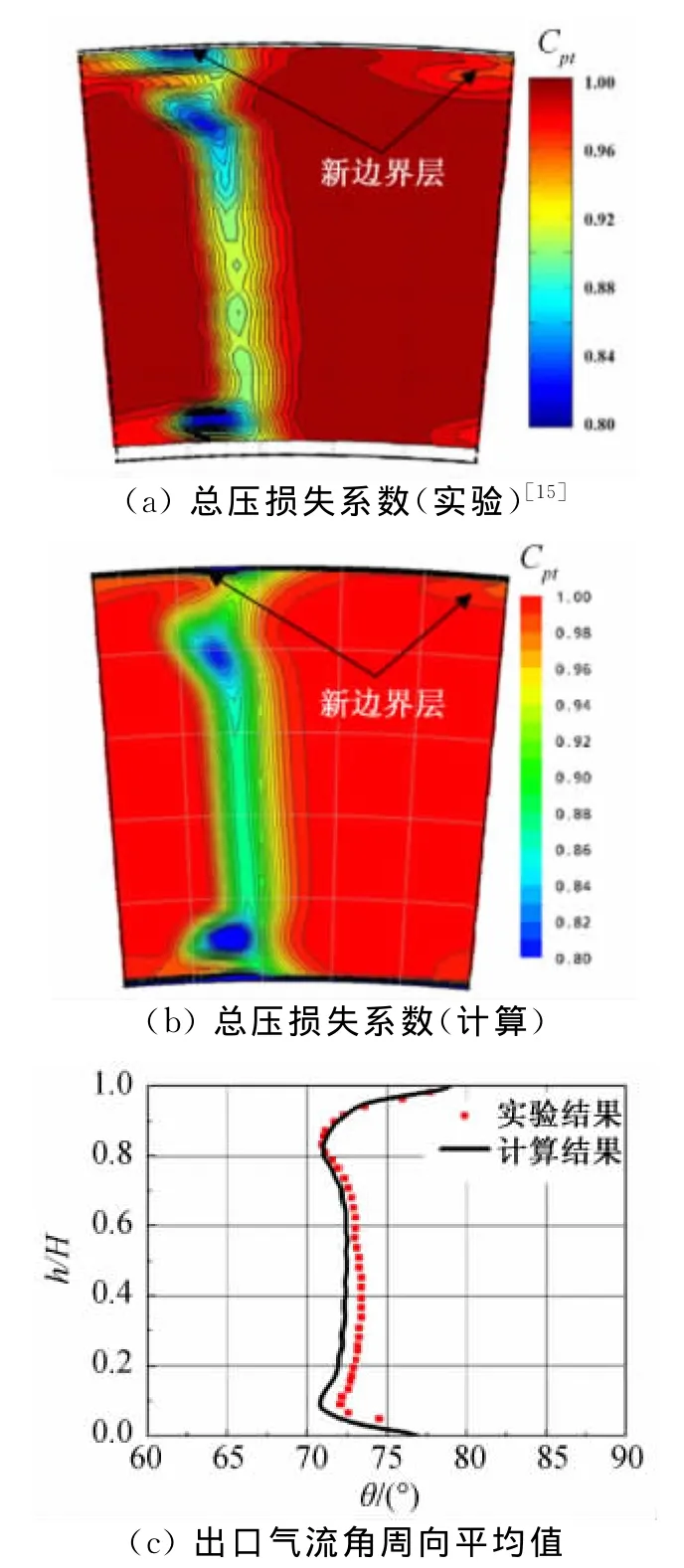
图2 导叶1出口总压损失系数和相对气流角分布Fig.2 Stagnation pressure loss coefficient and relative flow angle distributions at stator 1exit

图3给出了非定常时均结果动叶1出口（距尾缘约22%叶中轴向弦长位置，下同）计算和实验的比较。图3（a）和（b）分别为计算结果和实验结果出口总压损失系数分布，图中也将一个叶片通道沿径向和周向都划分为5等份。图中显示，计算结果与实验结果的二次流结构吻合的较好，转子出口二次涡分布十分明显，除了叶中附近的动叶尾迹，其他区域基本都被二次涡占据。轮毂和机匣通道涡均占据了50%以上周向区域，叶尖泄漏涡则更大，超过60%周向通道范围。

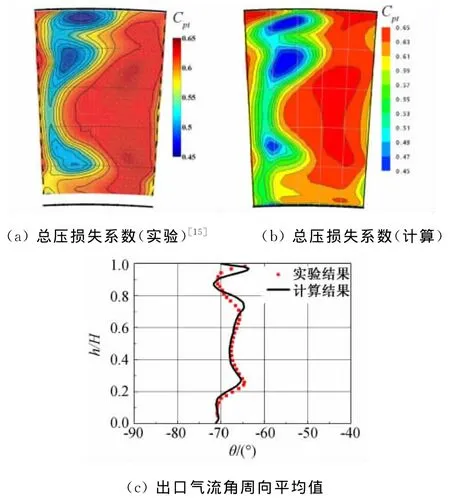
图3 动叶1出口总压损失系数和相对气流角分布Fig.3 Stagnation pressure loss coefficient and relative flow angle distributions at rotor 1exit

图3（c）为动叶1出口相对气流角的周向平均值分布。图中显示0～70%叶高区域计算结果与实验结果吻合的很好，轮毂通道涡引起的相对气流角变化约6°。70%叶高以上区域计算与实验在定量上存在一定差别，计算结果二次涡引起的气流角变化比实验结果略大，且二次涡在径向的分布也存在一定差别，产生这一现象的原因可能主要来自两方面：一是计算对上游导叶1新的边界层模拟不够精确，从而引起下游动叶1的进口条件发生了改变；二是计算对叶尖间隙附近的复杂强剪切流动模拟的不够精确。

从气流角分布可以看出，动叶1出口流动受二次流影响的程度大于导叶1，仅仅在40%～60%叶高区域气流角沿径向变化不大，其余叶高范围内气流都有明显的偏转。在10%～40%叶高区域受轮毂通道涡影响流动朝端壁过转、朝叶中欠转。叶尖区域的流动更加复杂，在60%～85%叶高区域受机匣通道涡影响流动朝端壁过转、朝叶中欠转，在85%叶高与机匣之间的区域受叶尖泄漏涡影响流动朝端壁欠转、朝叶中过转。

2.2 下游位势场对端区流动的非定常作用机理

2.1节的分析表明本文的数值模拟结果真实可信。下面通过分析动叶1＋导叶2的非定常计算结果，探讨下游导叶前缘位势场对动叶端区二次流的非定常作用机理。

图4给出了动叶1出口截面三个叶高处的静压和熵增时空分布。图中25%、70%和95%叶高分别对应着时均结果轮毂通道涡、机匣通道涡和叶尖泄漏涡核心区所在叶高处，横坐标表示动叶周向位置的无量纲数，纵坐标表示时间的无量纲数（等同于下游导叶周向位置的无量纲数），其中T为动叶经过下游一个静子通道的时间。从右下角到左上角分布的点划线代表各瞬时时刻下游导叶前缘所在周向位置，虚线A－A代表动叶出口主流中某点随时间的变化，B－B代表该叶高处的二次涡核心位置随时间的变化。

在不考虑动叶通道内流动自身的非定常性前提下，当动叶不受下游导叶非定常作用时，静压和熵增分布不随动叶－导叶相对位置的变化而改变，此时时空图中的等值线应该沿着竖直方向分布，而图4中的分布则不同，从图中可以观察到以下现象：

（1）B－B附近区域分别对应轮毂通道涡、机匣通道涡和叶尖泄漏涡，与主流区相比，这些二次涡区域静压减小，熵增增大。比较不同叶高位置的时空图可以看出，叶尖泄漏涡的熵增最大，轮毂通道涡的熵增最小，静压分布差别较小。

（2）动叶出口静压分布随时间（即动叶与下游导叶周向相对位置变化）周期性脉动。在导叶前缘附近，动叶出口静压增大；在通道中间时，动叶出口静压减小。

（3）动叶出口二次涡中的熵增随时间（即动叶与下游导叶周向相对位置变化）周期性变化。在导叶前缘附近，二次涡中的熵增减小；在通道中间时，二次涡中的熵增增大。熵增的变化规律恰好与静压相反。

为了更加清楚地反映不同叶高静压和熵增随时间的脉动量大小，图5给出了图4（b）中虚线A－A和B－B的静压分布以及B－B的熵增分布，横坐标为时间的无量纲数，纵坐标代表机匣通道涡核心区的静压值和熵增值。图中用点划线标出了经过导叶前缘的时刻，虚线代表时间平均静压值和熵增值。

从静压分布可以看出，随着动叶与导叶周向相对位置的推移，机匣通道涡核心处的静压和熵增值均呈周期性变化，并且当通道涡位于导叶前缘附近时，静压值增大，熵增值反而减小；当通道涡位于导叶通道中间时，静压值减小，熵增值反而增加。

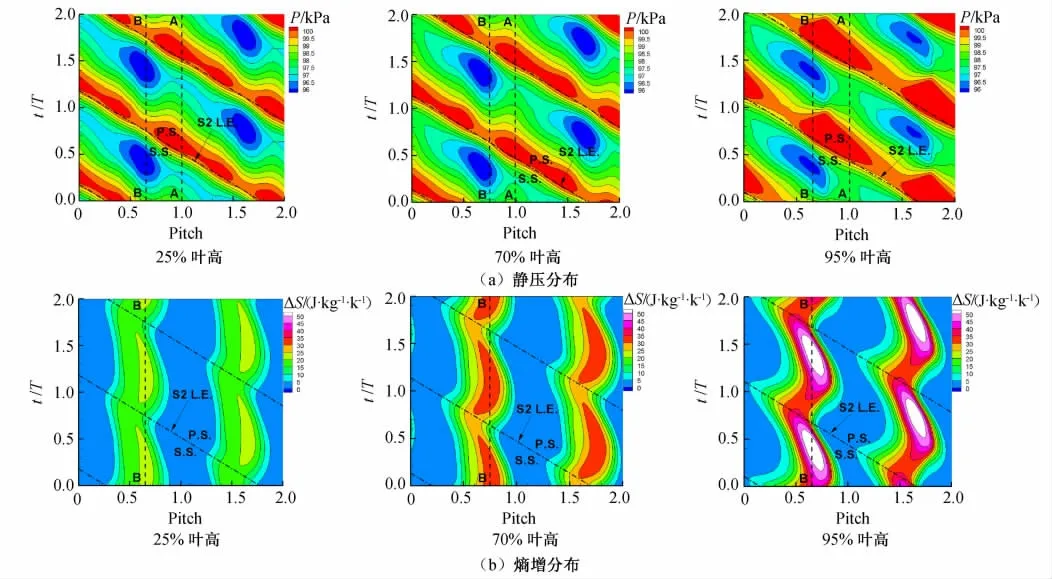
图4 动叶1出口不同叶高位置静压和熵增分布时空图Fig.4 Space－time diagram for static pressure and entropy rise at rotor 1exit

为了进一步了解熵增随时间的变化规律，图6给出了时均结果二次涡核心处的熵增随时间变化（B－B线）的频谱分析，横坐标为导叶通过频率的无量纲数，纵坐标为熵增脉动量占时均熵增值的比值。

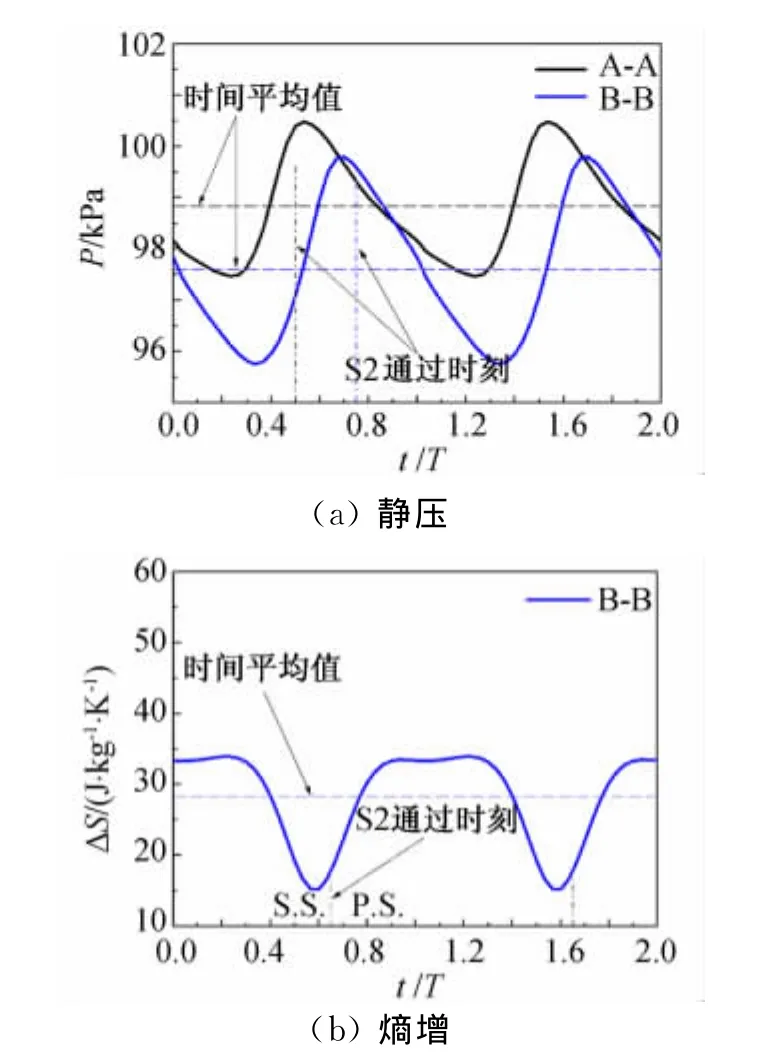
图5 70%叶高动叶1出口二次涡核心位置静压和熵增随时间的变化（B－B）Fig.5 Static pressure and entropy rise across section B－B

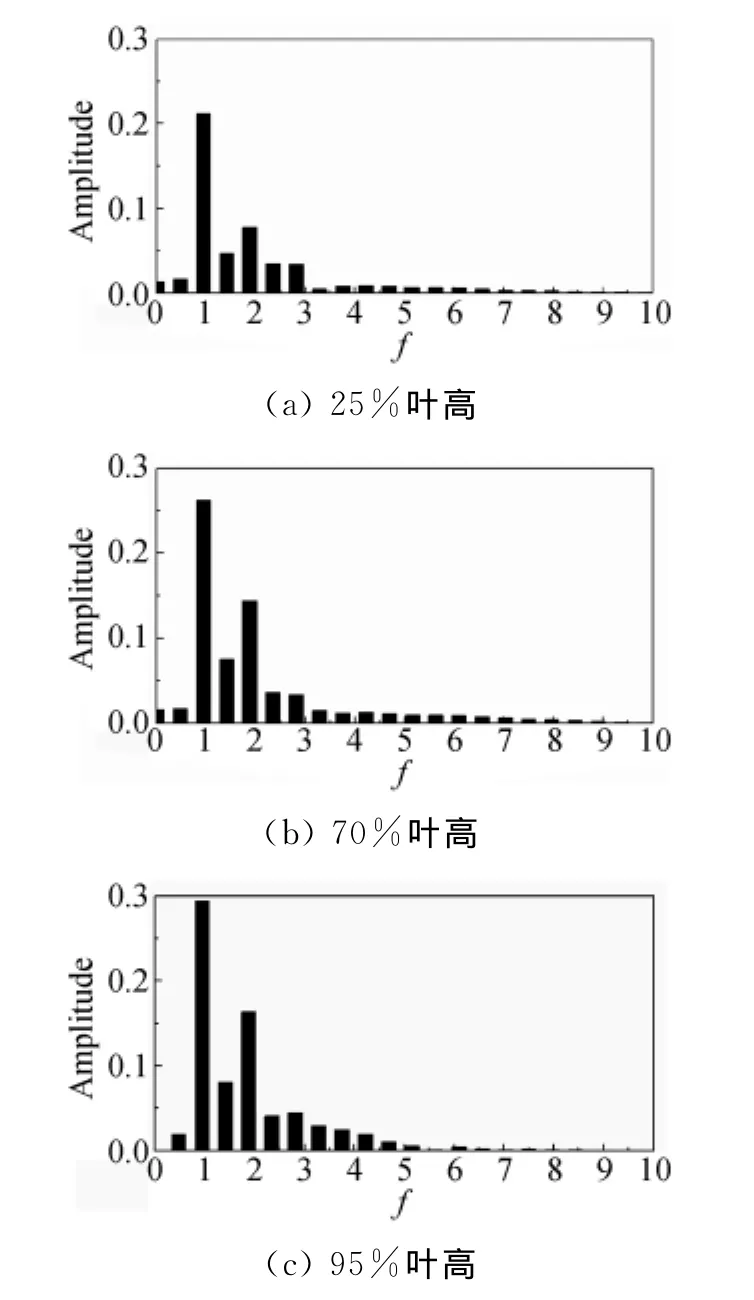
图6 动叶1出口二次涡核心位置（B－B线）熵增值频谱分析Fig.6 Power spectrum of entropy rise across section B－B

图中显示熵增脉动值最大对应下游导叶相对通过频率，由此证明二次涡中的非定常性主要来自于下游导叶的非定常位势作用。轮毂通道涡、机匣通道涡和叶尖泄漏涡中的熵增脉动量占时均值的比例，随着时均结果熵增值的增大而增加，说明二次涡损失受下游非定常位势作用影响的程度，随着二次涡时均结果损失值的增大而增加。

上述分析显示，受下游导叶的非定常位势作用影响，动叶1出口二次涡损失呈周期性变化。由于二次涡损失与二次涡的旋涡强度密切相关，在通道涡和泄漏涡中，流向涡的影响占主要地位，因此，下面利用简单的旋涡运动学理论，分析流向涡量随时间的变化规律，解释下游导叶非定常位势场影响动叶出口二次涡损失的物理机制。经过一系列合理的假设，涡量ω随时间的变化可以用涡量方程表示为［16］：

其中u表示速度矢量，ν表示运动粘性系数。等号右边第一项ω·▽u代表旋涡的拉伸和压缩，第二项ν·Δω代表粘性对涡量的影响。由于位势作用是无粘的，因此只考虑旋涡拉伸和压缩对涡量的影响。

下面简单分析不可压加速流场中流向涡管的变化规律，如图7所示。由涡管中流量守恒得到：

根据开尔文环量守恒定理：

由此可以推导出：

上式表明，当ue＞ui时，ωe＞ωi，即流向涡管在加速流中涡量增大；反之，在减速流中涡量减小。

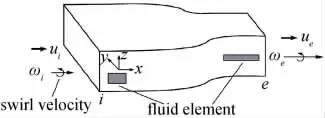
图7 流向涡在加速流场中的变化示意图［17］Fig.7 Schematic diagram for streamwise vortex development in accelerated flow field

下面根据方程（5）的结论分析动叶1出口二次涡损失的变化规律，以机匣通道涡为例。图8给出了70%叶高截面两个瞬时时刻的静压和熵增分布，左图为静压分布，右图为熵增分布。图中显示动叶出口存在机匣通道涡产生的高损失区，重点观察虚线圆圈所示区域的流场变化。

在t／T＝0.667时刻，通道涡向下游运动时经过静子通道中间、偏向导叶吸力面的位置。静压分布显示，受下游导叶位势作用影响，动叶出口静压沿流向减小，流动呈现加速、减压的趋势。根据方程（5）的结论可知，通道涡在加速流中流向涡量增大，速度亏损增大（流动掺混损失与速度差ΔV的平方ΔV2成正比［2］），从而增大了通道涡中的熵增。

在t／T＝1.0时刻，通道涡运动到下游导叶前缘附近，此时的流动特征与t／T＝0.667时刻相反。受下游导叶位势作用影响，动叶出口静压沿流向增大，流动呈现减速、增压的趋势。通道涡在减速流中流向涡量减小，速度亏损减小，从而通道涡中的熵增也减小。

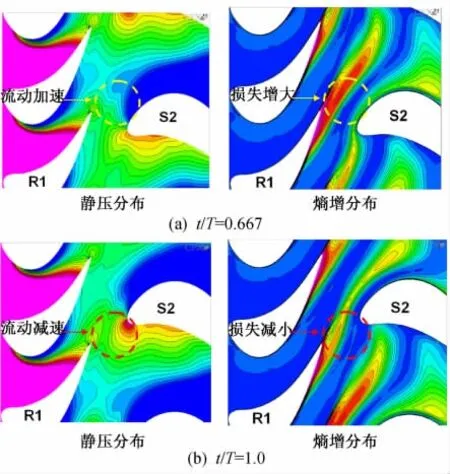
图8 70%叶高截面非定常瞬时静压和熵增分布Fig.8 Unsteady static pressure and entropy rise distributions at 70%blade span

图9为动叶1出口不同瞬时时刻熵增和二次流速度矢量分布，其中二次流速度矢量近似定义为当地速度矢量与截面平均速度矢量之差。图中分别给出了动叶尾缘和下游导叶前缘的周向位置，其中云图的左、右边界分别为动叶尾缘吸力面和压力面一侧，黑色实线为导叶前缘的周向位置。

从图中可以看出，由于动叶出口不同类型的二次涡（包括轮毂／机匣通道涡、轮毂／机匣壁面涡、叶尖泄漏涡）所处周向位置不同，它们受下游导叶位势作用影响导致的最大损失和最小损失时刻也不相同。在t／T＝0.25时刻，轮毂／机匣壁面涡恰好位于导叶前缘附近，旋涡沿流向减速增压，因此流向涡量减小，掺混损失减小，这一时刻轮毂／机匣壁面涡中的损失为四个时刻中的最小值。在t／T＝0.5和t／T＝0.75时刻，动叶出口二次涡均位于通道中间位置，旋涡沿流向加速减压，因此流向涡均增大，二次涡中的掺混损失与其它两个时刻相比有所增大。在t／T＝1.0时刻，轮毂／机匣通道涡和叶尖泄漏涡靠近下游导叶前缘，由于流动减速增压，流向涡量减小，旋涡的掺混损失也相应减小。

图10进一步给出了动叶1出口截面熵增和流向涡绝对值的周向平均值时空分布。左图中横坐标为时间的无量纲数，纵坐标为叶高的无量纲数；右图显示了时空图中某两个瞬时时刻（如虚线C1－C1和C2－C2所示）的周向平均值分布。观察发现图中主要存在以下现象：

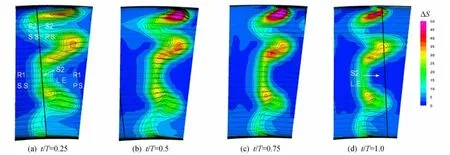
图9 动叶1出口非定常瞬时熵增和二次流速度矢量分布Fig.9 Entropy rise and secondary flow vectors distributions at different time steps at rotor 1exit

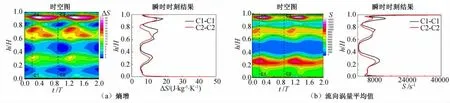
图10 动叶1出口熵增和流向涡量绝对值的周向平均值分布Fig.10 Pitchwise averaged result of entropy rise and streamwise vorticity distributions at rotor 1exit

（1）受下游导叶位势作用影响，动叶出口截面的周向平均值分布随时间周期性变化，如右图所示，在t／T＝0.2（C1－C1）和t／T＝0.9（C2－C2）两个时刻，熵增沿径向的分布存在明显差别，前一时刻的出口损失明显高于后一时刻。

（2）二次涡损失与流向涡量密切相关。在t／T＝0.2时刻（C1－C1）附近，轮毂／机匣通道涡中熵增和流向涡量绝对值均达到一个周期的最高水平；在t／T＝0.4时刻附近，叶尖泄漏涡中的熵增和流向涡量绝对值最大；在t／T＝0.8～1.0时间范围内，整个叶高区域的熵增和流向涡量绝对值相对较小。

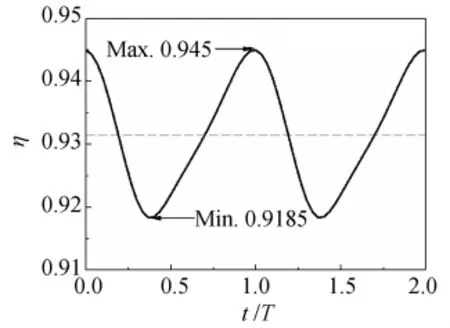
图11 动叶1出口截面平均效率随时间的变化Fig.11 The variation of section averaged efficiency with time

图11为动叶1出口一个通道截面平均的效率随时间变化曲线，图中给出了两个周期内的变化过程。从图中可以看出，效率的最大值和最小值分别出现在t／T＝1.0时刻和t／T＝0.375时刻，这与图10中所示的结果基本吻合，计算表明动叶出口效率随时间的脉动量达到2.65个百分点。

3 结 论

本文通过数值模拟方法对下游位势场与涡轮端区二次流和泄漏流的非定常相互作用机理进行了研究，主要得到以下结论：

（1）1.5级涡轮非定常计算结果与实验结果总体来说符合的较好。计算与实验在定量上的差别表明，在研究涡轮端区复杂精细流动时，有必要考虑细节结构对流场的影响，所采用的数值模拟方法对叶尖间隙等处复杂强剪切流动的模拟精度有待进一步提高。

（2）在亚声速涡轮级中，下游非定常位势作用使得转子出口二次涡结构呈现明显的周期性变化，转子出口总熵增和效率均随时间发生改变。

（3）转子出口性能的周期性变化主要来源于位势作用对转子轮毂端区和叶尖区域二次涡的非定常影响，当二次涡位于导叶前缘附近时，流动沿流向减速增压，旋涡中的流向涡量减小，二次涡损失减少；当二次涡位于导叶通道中间时，流动沿流向加速减压，旋涡中流向涡量增大，二次涡损失相应增加。

［1］PULLAN G，DENTON J，CURTIS E.Improving the performance of a turbine with low aspect ratio stators by aft－loading［R］.ASME Paper 2005－GT－68548.

［2］DENTON J D.Loss mechanisms in turbomachines［J］.Journal of Turbomachinery，1993，115：621－656.

［3］HAWTHORNE W R.Rotational flow through cascade，part I：The components of vorticity［J］.Journal of Mechanics and Applied Mathematics，1955，8：266－279.

［4］SHARMA O P，BUTLER T L.Predictions of endwall losses and secondary flows in axial flow turbine cascades［J］.Journal of Turbomachinery，1987，109：229－236.

［5］WANG H P，OLSON S J，GOLDSTEIN R J，et al.Flow visualization in a linear turbine cascade of high performance turbine blades［J］.Journal of Turbomachinery，1997，119：1－8.

［6］SIEVERDING C H.Recent progress in the understanding of basic aspects of secondary flows in turbine blade passages［J］.Journal of Engineering Gas Turbines Power，1985，107：248－257.

［7］LANGSTON L S.Secondary flows in axial turbines—a review［J］.Annals of the New York Academy of Sciences，2006，934：11－26.

［8］KORAKIANITIS T.On the propagation of viscous wakes and potential flow in axial－turbine cascade［J］.Journal of Turbomachinery，1993，115（1）：118－127.

［9］MILLER R J，MOSS R W，AINSWORTH R W.Wake，shock and potential field interactions in a 1.5stage turbine，Part I：Vane－rotor and rotor－vane interaction［R］.ASME Paper GT2002－30435.

［10］SCHLIENGER J，KALFAS A L，ABHARI R S.Vortex－wake－blade interaction in a shrouded axial turbine［J］.Journal of Turbomachinery，2005，127：699－707.

［11］OPOKA M M，HODSON H P，THOMAS R L.Boundary layer transition on the high lift T106ALP turbine blade with an oscillating downstream pressure field［R］.ASME Paper GT2006－91038.

［12］OPOKA M M，HODSON H P.Transition on the T106 LP turbine blade in the pressure of moving upstream wakes and downstream potential fields［R］.ASME Paper GT2007－28077.

［13］邹正平，叶建，张永新，等.非定常流动对叶片表面负荷分布影响的数值模拟研究［J］.燃气涡轮试验与研究，2006，19（1）：21－26.

［14］周莉，蔡元虎.不同轴向间距下涡轮级内非定常流场的数值研究［J］.燃气涡轮试验与研究，2010，25（3）：629－635.

［15］BEHR T.Control of rotor tip leakage and secondary flow by casing air injection in unshrouded axial turbines［D］.［D.Phil.Thesis］.Dresden University of Technology，2007.

［16］GREITZER E M，TAN C S，GRAF M B.Internal flow：concepts and applications［M］.Cambridge：Cambridge University Press，2004.