推力转向喷流与高速主流干扰参数影响规律的数值模拟研究

司芳芳，袁先旭，李建强，陈 琦

（中国空气动力研究与发展中心，四川 绵阳 621000）

0 引 言

新一代战斗机要求具有良好的机动性和短距离起降性能。在进行大迎角机动飞行时，飞机绕流现象复杂，流动分离严重，垂尾等操纵面浸没在尾迹流动之中，操纵面效率急剧降低甚至完全失效，通过操纵面偏转获得所需控制力和力矩的方法，已经很难满足大迎角机动的要求，必须采用推力矢量控制技术。推力矢量技术作为第四代战斗机设计的一项关键技术，从上个世纪八十年代开始，美国就开展了广泛的研究，包括理论与计算分析、缩比模型试验、飞行模拟器仿真和飞行演示验证等多种手段，并已成功应用于F－22、F－35等第四代主力战机中。

现代战斗机的大后掠角、尖前缘的机翼气动布局在较大迎角下会产生前缘涡，在加装推力转向喷管后，矢量喷流的引射作用，使前缘涡的位置向内和向下移动，即向机身方向移动；再加上涡对的诱导作用，会减少机翼后缘的逆压梯度，使前缘涡涡核轴向速度增加，前缘涡旋紧，涡强增强，对翼面流动的诱导能力增强；在破裂涡流动状态，矢量喷流对主流影响最大，可能使前缘破裂涡恢复，从而引起超环量效应。在实际飞行中，推力转向尾喷流和主流之间，特别是在飞行攻角较大或来流马赫数较高时，喷流和外流之间产生强干扰，从而形成复杂的涡系，波系和分离流，同时改变了喷管内流状态，使激波、分离波系产生位置发生变化，并使机身压力分布发生变化，影响飞机的整体气动特性。我们知道，后机身流场是纵向力矩系数的主要影响因素，它对喷管内流压力变化很敏感，因此，必须考虑矢量喷管推力及控制力矩对整个机身的压力分布的影响，将矢量喷管与飞机外形的气动布局型式结合起来研究，以提高矢量喷管的推力效率及飞机性能。值得注意的是，推力矢量尾喷流干扰效应与传统喷管的喷流干扰效应是相当不同的［1］，传统喷管的喷流干扰效应是一种局部的弱扰动，仅集中在喷管出口附近的区域；而推力矢量尾喷流干扰效应则是一种强扰动，对战斗机的整体气动特性有相当大的影响，这种影响并强烈依赖于机身／推进系统的集成设计，如F－22战斗机就细致设计了双发喷管的间距（小间距设计），并通过加长尾锥来隔离双发喷流的干扰。无疑，研究主流与推力矢量尾喷流的干扰效应规律和机理将是机身／推进系统优化集成设计的基础。

为此，针对推力转向喷管开展尾喷流／主流干扰对全机气动特性影响研究，具有较高的学术价值和重要的应用价值，可为推力矢量技术的工程应用乃至先进飞行器的研制奠定技术基础。

1 计算方法

当战斗机利用推力矢量技术进行大迎角过失速机动时，推力转向喷流与高速主流干扰流场极为复杂，真实的物理过程包括大范围湍流分离流、多相流、高低温气体掺混流动、内外流干扰、激波／膨胀波／剪切层／旋涡干扰等。要想完全真实模拟，对数值计算模型和计算方法有很高的要求。这里与拟开展的高速风洞试验研究相同，采用了冷喷模拟方法，对数值模拟方法的要求主要是精细的网格、高精度的计算格式和适用的湍流模型。

1.1 数值方法

控制方程为可压缩的N－S方程。空间离散采用Steger－warming通量差分，采用 minmod限制器，MUSCL插值采用二阶插值，时间离散采用LU－SGS方法。鉴于目前DNS、LES和RANS存在的问题，本文选用课题组自主研发的一种基于分区混合和基于湍流尺度混合的双重RANS／LES混合模型，该模型经过典型算例的验证，计算结果均与试验和文献计算结果符合较好，表明该RANS／LES混合模型能给出较合理的湍流宏观平均量，值得探索用于推力转向喷流与高速主流干扰效应的数值模拟研究的实际工程问题中。方法细节可参见文献［2］。

1.2 边界条件

远场采用无反射边界条件；壁面采用无滑移、绝热壁边界条件；计算需要进行全流场计算，对称子午面为块边界，采用一一对接边界条件。可以证明，上述边界条件处理方法不引入非对称误差。矢量喷管出口设为喷流入口边界，给定参数有喷流的压强pj，密度ρj，速度Vj和喷流偏转角δj。入口边界条件是由已知的喷流总压Ptj、总温Ttj和喷流马赫数Mj按一维等熵流公式计算得到：

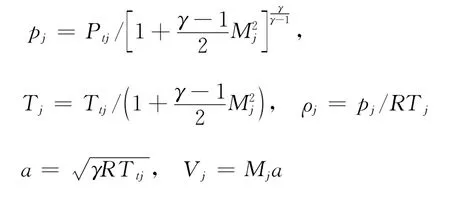
本文使用的喷流入口条件，未考虑矢量喷管内流与主流干扰情况，并不符合实际喷流情况。实际情况下，外流将影响喷管内流场的建立，下一步将对喷管内流和主流的干扰进行深一步研究。

1.3 计算模型和网格

首先依据图纸，生成本文的计算用数模，按计划分别计算了矢量喷管无偏转（δj＝0°）、向下偏转10°（δj＝－10°）、向下偏转20°（δj＝－20°）和向下偏转30°（δj＝－30°）的情况。

在进行数值模拟时，首先要尽量减小网格对计算结果的影响。为了保证计算的精度和效率，采用结构化网格生成技术，由于研究对象几何形体的复杂性，采用了多块搭接网格，且只计算半流场。为准确模拟喷流干扰区的尺度，应保证足够的干扰区附近流向的网格密度，所以在模型的头部、翼尖、壁面和尾部喷口附近局部加密。图1为喷管偏转不同角度时网格的空间分布，网格数量都约为709.19万，在空间分为6块，上游距飞机头部3.0L，下游距尾喷管4.0L，远场边界距中心线3.0L。

图1 局部放大的计算网格Fig.1 The computation grid with local zoom

1.4 计算条件

喷流对全机气动干扰是由内、外流的相互作用所引起的。通常情况下，喷流与主流气体的理化特性并不完全相同，喷流介质的组分、分子量、化学反应和热力学特性等因素都会对干扰流场的动力学和热力学输运特性及内、外流掺混过程产生影响，使流动复杂化。为了与后续风洞试验研究保持一致，本文从喷流、主流均为完全气体的简单情况入手，数值模拟推力转向尾喷流与高速主流干扰的复杂流场。主流和尾喷流条件的主要参数见表1，主流条件由标准大气表计算。

表1 主流、喷流计算条件Table 1 The computation condition of main flow and jet flow

2 计算结果和分析

2.1 来流马赫数影响

以攻角为15°，喷口总压为300kPa，喷口总温为300K，喷流马赫数为1.0为例，对不同来流马赫数的计算结果进行对比和分析。

图2（a～f）分别给出了不同来流马赫数时马赫数等值线分布，从图中可以看出，本文计算结果显示了非常清晰的流场，刻画出了喷口附近复杂的波系结构。可以得出如下结论：

图2 马赫数等值线Fig.2 Mach number contours

（1）随来流马赫数数增大，主流与尾喷流干扰效应明显增强。M＝0.4、δj＝0°时，主流虽有15°攻角，但对尾喷流几乎没有影响，压力标识的喷流尾迹几乎成一条直线向后传播，清晰尾迹区达约全机长的一半；M＝0.6的情况与 M＝0.4基本相似；M＝1.5时，情况则有明显变化，主流遭遇尾喷流膨胀波包，迎风侧紧临喷管出口截面，产生一道斜激波，导致喷流尾迹向上倾斜，实际推力矢量角发生损失；随着主流M进一步增大，这一现象愈发明显。造成这一现象的主要原因在于随M增大，主流动压增大，对喷流尾迹吹拂能力加强。

（2）随来流M数增大，喷流波系结构发生明显变化。M＝0.4时，喷流出口膨胀后形成马赫盘（从二维对称面来看，为正激波），随M增大，马赫盘不断缩小，到M＝1.5时，几为斜激波相交的鱼尾波系形态。随着M进一步增大，斜激波相交的鱼尾波系形态愈发明显。造成这一现象的主要原因在于随M增大，喷管出口环境压力降低，喷流出口后的继续膨胀增强。

（3）当δj增大时，喷流干扰流场结构与喷流／主流干扰效应随M的变化规律与δj＝0°的情况基本一致。但当δj＞0°后，基于现模型设计方案，喷管与机身之间的弯折角对主流有明显影响，特别是当M＞1后，此处产生一道强压缩激波，明显改变主流和喷流的流场结构。但实际情况下，喷管偏转时不可能有这样明显的弯折角，模型设计的失真有何影响，需进一步深入研究。

图3（a～e）给出了δj＝0°、δj＝－20°、δj＝－30°时飞机气动力系数随来流马赫数的变化，图3（f）给出了δj＝0°、δj＝－10°、δj＝－30°时推力矢量角损失随来流马赫数的变化。可以看到：

（1）推力矢量喷管偏转不同角度时，对升力系数和法向力系数影响很小，对轴向力和俯仰力矩的影响稍大。表明在高速主流条件下，攻角不大时，推力转向喷流对主流的干扰局限于尾部局部区域，不明显。这与文献中低速推力矢量试验研究的结论一致。

图3 气动力系数随M变化Fig.3 Aerodynamic coefficient variation with M

（2）推力矢量角损失量随喷管偏转角度的增大而增大，随来流马赫数的增大而急剧增大。当来流马赫数为0.4和0.6时，推力矢量角的损失较小，表明推力转向控制效率很高。但当来流马赫数超过声速时，推力矢量角损失严重，在 M＝2.0、δj＝－30°情况，推力矢量角损失最大接近18°，表明此时喷管虽下偏30°，但实际俯仰方向的推力矢量只有下偏12°，效率很低。这说明推力矢量技术有一定的适用范围，超过某个临界M后，推力矢量技术代价较高，效率降低。

2.2 飞行攻角影响

显而易见，飞行攻角也是一个重要的主流影响参数。实际上，推力矢量技术的一个重要考核即在大攻角操纵面效率降低时提供操纵力矩。这里，以喷口总压为300kPa，喷口总温为300K，喷流马赫数为1.0为例，对来流马赫数为0.6时飞行攻角在－10°～40°之间和来流马赫数为2.0时飞行攻角在－10°～15°之间时的计算结果进行对比。

图4（a～f）、图5（a～c）给出了不同条件下用压强着色的空间流线图。通过对主翼背风涡流形态的比较分析，可以认为：

（1）M＝0.6、无喷流时，随攻角增大，背风集中涡逐渐增强，低压区范围逐渐覆盖几乎整个上翼面，当攻角达40°，背风集中涡破裂，上翼面为破裂后的随机尾迹流动覆盖，流线压力也明显升高。这一演化过程符合众所周知的三角翼背风涡流演化规律，表明本文基本流场计算是可靠的。

（2）对比δj＝0°和δj＝－20°与无喷流时的流场结构，攻角为20°和30°情况下，三者并无明显区别，表明在中等攻角下，主翼上表面背风集中涡较强，此时，尾喷流对主流的干扰（引射效应）较弱。当攻角为40°时，情况则明显不同，无喷流时主翼上表面背风集中涡已破裂，无明显集中涡形态和低压区，但有喷流时，机翼上流动又恢复出现明显集中涡形态和低压区（有喷流流场是以无喷流流场为初场继续计算得到），表明在40°攻角情况下，推力转向喷流的后缘引射效应比较明显，使得已破裂的背风集中涡恢复，在外形上呈现出超环量效应。文献中低速风洞试验研究表明在低速大攻角情况下，推力转向喷流的引射效应可使破裂的主翼集中涡重新恢复成集中涡形态，诱导出超环量效应，对全机气动特性影响很大。但从图6可以看出，攻角对气动力系数的影响较小，这说明对于该简化模型，在高速主流情况下，推力转向喷流的影响相对较小，从定量上不足以说明产生了超环量效应。可能原因是简化模型的主翼比较靠前，尾喷流对其影响较小；或主流M较高时，推力转向喷流的影响减弱。

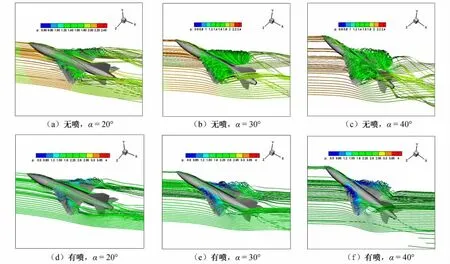
图4 δj＝0°，M＝0.6时用压强着色的流线图Fig.4 Streamlines colored by pressure forδj＝0°，M＝0.6

图5 δj＝－20°，M＝0.6时用压强着色的流线图Fig.5 Streamlines colored by pressure forδj＝－20°，M＝0.6

图6（a～e）分别给出了M＝0.6和M＝2.0在推力转向喷流影响下的气动力系数随攻角的变化。图6（f）给出了M＝0.6和M＝2.0时推力矢量角损失随攻角的变化。

经分析，可得出以下结论：

（1）推力转向喷流对轴向力的影响较大，这与轴向力系数的积分方式有关，这里在无喷流情况下，将喷管侧面和底部都进行了积分，与试验天平受力不一致。但不同喷流偏转角有相互之间的比较意义。M＝0.6时，在攻角大于20°以后，不同喷流偏转角对气动力特性的影响才比较明显，这与上面的流场结构分析基本一致。M＝2.0时，不同喷流偏转角导致的尾部激波形态与强度明显不同，因而在计算的攻角范围内，喷流偏转角对轴向力系数都有明显影响，并随攻角增大而增大，但对其他气动力分量则几乎没有影响，表明超声速情况下，喷流与主流干扰局限在尾部局部区域，没有亚声速条件下出现的超环量效应。究其机理，这与超声速情况下，机翼的流动形态是相关的，M＝2.0时，三角翼背风区并无明显集中涡形态，也与扰动在超声速条件下只向后传播有关。

（2）推力矢量角损失随攻角增大而增大，除此以外，也与矢量喷管偏转角、来流主流M 高度相关，推力矢量喷管偏转角越大、来流马赫数越高，推力矢量角的损失就越大，即实际推力矢量角与原推力矢量角的差别越大。但推力矢量角的损失程度在M＝0.6与M＝2.0时差别极为显著，M＝0.6时，推力矢量角总的来说损失不大，在计算范围内最大不超过4°，但M＝2.0时，推力矢量角损失相当大，最大可达18°，再次验证了在超声速条件下使用推力矢量技术代价高，实际上不可行。

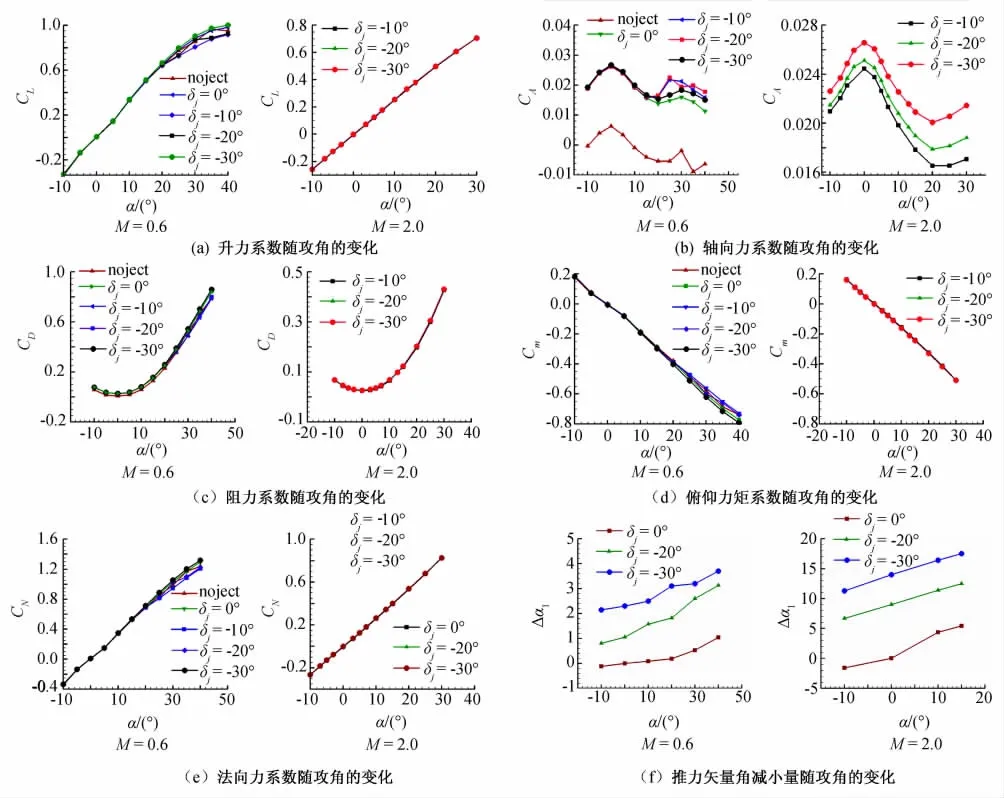
图6 气动力系数随α变化Fig.6 Aerodynamic coefficient variation withα

2.3 喷流总压

为考察喷流总压的影响，以来流马赫数为0.6和2.0，攻角为15°，喷口总温为300K，喷流马赫数为1.0为例，比较和分析喷口总压分别取300kPa、400kPa、500kPa时对飞机气动力系数的影响。

图7（a～d）分别给出了喷口总压分别取400kPa和500kPa时流场的马赫数等值线分布。图8分别给出来流马赫数为0.6和2.0，δj＝0°，－10°，－20°，－30°时，气动力系数随喷流总压的变化。总的来看，可有如下结论：

（1）喷流总压对尾喷流流场结构有所影响，但并不改变流场结构的拓扑形态，只是强度有所不同。喷流总压增大时，由于喷流马赫数固定，则喷管出口静压增大，喷流出喷口后，进一步膨胀的能力加强，即喷流的穿透力增强。因此，M＝0.6时，总压增大，喷流马赫盘增大；M＝2.0时，总压增大，斜激波相交点后移。

（2）由于总压对流场结构没有明显改变，因此，总压变化对全机气动力特性的影响甚小，几乎可忽略不计。

图7 δj＝－10°时马赫数等值线分布图Fig.7 Mach number contours forδj＝－10°

图8 气动力系数随P0变化Fig.8 Aerodynamic coefficient variation with P0

2.4 喷流马赫数

为考察喷流马赫数的影响，以来流马赫数为0.6和2.0，攻角为15°，喷口总压为300kPa，喷口总温为300K为例，比较喷流马赫数在1.0～2.8之间取值时对飞机气动力系数的影响。

图9（a～d）分别给出了喷流马赫数为1.2和2.0时流场的马赫数等值线分布。图10分别给出了来流马赫数为0.6和2.0，δj＝0°，－10°，－20°时，气动力系数随喷流马赫数的变化。总的来看，可有如下结论：

（1）喷流马赫数对尾喷流流场结构有明显影响，甚至改变流场结构的拓扑形态。喷流马赫数增大时，由于喷流总压固定，则喷管出口静压减小，喷流出喷口后，进一步膨胀的能力减弱，即喷流的穿透力减弱。因此，M＝0.6时，喷流马赫数增大，喷流马赫盘减小，Mj＝1.2时，马赫盘即已消失，成为斜激波相交形态，Mj进一步增大，则斜激波相交点前移；M＝2.0时，喷流马赫数增大，斜激波相交点前移。

（2）喷流马赫数虽对流场结构有明显改变，但局限于喷管以后的喷流尾迹区域，因此，喷流马赫数变化对全机气动力特性的影响甚小，几乎可忽略不计。

图9 δj＝－20°时马赫数等值线分布图Fig.9 Mach number contours forδj＝－20°

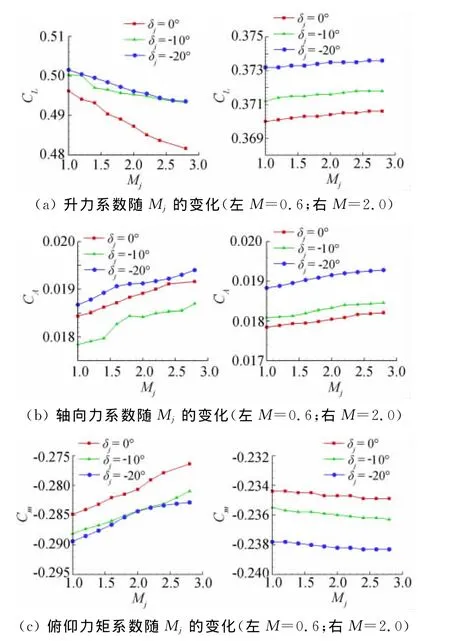
图10 气动力系数随Mj变化Fig.10 Aerodynamic coefficient variation with Mj

2.5 喷流总温

为考察喷流总温的影响，以来流马赫数为0.6和2.0，攻角为15°，喷口总压为300kPa，喷流马赫数为1.0为例，对喷口总温分别取300K、900K、1200K、1800K时的计算结果进行比较和分析。

图11（a～f）给出了不同喷口总温时流场的温度等值线分布。图12分别给出了来流马赫数为0.6和2.0时气动力系数随喷流总温的变化。总的来看，可有如下结论：

（1）喷流总温对尾喷流流场结构有一定影响，甚至改变流场结构的拓扑形态。喷流总温增高时，喷管出口静温增高，由于喷流总压固定，喷管出口静压不变，根据状态方程，则喷管出口密度降低，喷流喷出后，进一步膨胀的能力减弱，即喷流的穿透力减弱。因此，M＝0.6时，喷流总温增高，喷流马赫盘减小，喷流总温达900K时，马赫盘即已消失，成为斜激波相交形态，喷流总温进一步增大，则斜激波相交点前移；M＝2.0时，喷流总温增大，斜激波相交点前移。

（2）喷流总温虽对流场结构有一定改变，但局限于喷管以后的喷流尾迹区域，因此，喷流总温变化对全机气动力特性的影响甚小，几乎可忽略不计。

图11 δj＝－10°时温度等值线分布图Fig.11 Temperature contours forδj＝－10°

图12 气动力系数随Tj变化Fig.12 Aerodynamic coefficient variation with Tj

3 结 论

本章针对一种简化战斗机风洞试验模型，开展了推力转向喷流与高速主流干扰的数值模拟研究，较为系统地研究了来流马赫数、飞行攻角、喷流总压、喷流马赫数、喷流总温、推力转向喷管偏转角等参数对流场结构和全机气动特性的影响规律。根据研究结果和研究体会，可小结如下：

（1）主要的影响参数是来流马赫数、飞行攻角、推力转向喷管偏转角和喷流落压比，其它参数的影响较小。

（2）对流场结构影响最大的参数是来流马赫数，其次是攻角和推力转向喷管偏转角。在来流马赫数为0.6时，在大攻角下，推力转向喷流的引射效应诱导出一定的超环量效应，但还需要进一步的验证。

（3）对推力矢量角损失影响最大的参数也是来流马赫数，其次是推力转向喷管偏转角和攻角。推力矢量角损失随马赫数、喷管偏转角和攻角的增大而增大。在超声速情况下，推力矢量角损失可超过喷管偏转角的一半以上，使得推力矢量技术效率降低。因此，在超声速条件下，推力矢量技术实际上并不可行。

（4）对全机气动特性影响最大的参数是攻角，其次是来流马赫数和推力转向喷管偏转角。但总的来说，由于简化战斗机的主翼为平板翼、尾喷管离主翼距离偏大，导致推力转向喷流／高速主流干扰效应对全机气动力系数的影响较小，对试验测量提出了很高的挑战。

以上结论对后续风洞试验有一定的指导意义，本文计算研究也需要进一步与试验研究相结合，相互校核，以提高计算结果的置信度。

［1］HILEY P E，WALLACE H W，BOOZ D E.Study of nonaxisymmetric nozzles installed in advanced fighter aircraft［J］.J.of Aircraft，1976，13（12）：1000－1006.

［2］司芳芳.推力转向喷流与高速主流干扰的数值模拟研究［D］.［硕士学位论文］.中国空气动力研究与发展中心，2010.

［3］FRED K，HARVEY S.X－31flight test update［R］.AIAA－92－1035.

［4］BOWERS A H，PAHLE J W.Thrust vectoring on the NASA F－18high alpha research vehicle［R］.NASA TM 4771，1996.

［5］CAPONE F，SMERECZNIAK P，SPETNAGEL D.Comparative investigation of multiplane thrust vectoring nozzles［R］.AIAA－92－3263.

［6］DEERE K A.Summary of fluidic thrust vectoring research conducted at NASA langley research center［R］.AIAA 2003－3800.

［7］连永久.射流推力矢量控制技术研究［J］.飞机设计，2008，28（2）：19－24.

［8］张群锋，吕志咏.轴对称矢量喷管外流对内流干扰研究［J］.航空动力学报，2003，18（3）：322－326.

［9］李栋，焦予秦，宋科.喷流－外流干扰流场数值模拟［J］.航空动力学报，2008，29（2）：292－296.

［10］王延奎，张永生.矢量喷流对细长体大迎角非对称流动影响研究［J］.力学学报，2007，39（3）：289－296.