转子陀螺效应对翼吊发动机机翼弯扭颤振特性影响研究

周健斌，章俊杰，孟 光

（1.中国商用飞机有限责任公司 上海飞机设计研究院，上海 201210；2.上海交通大学 机械系统与振动国家重点实验室，上海 200240）

0 引 言

具有陀螺效应的弹性体在航空、航天、机械等领域有广泛的应用。D′Eleuterio［2－6］和 Hughes［7］针对自旋航天器研究了一类具有分布陀螺力矩的弹性系统的动力学特性并提出了陀螺弹性系统的概念。Peck［8－9］等在此基础上提出了运用嵌入在结构中的角动量来实现结构自适应调谐，如频移、模态耦合和解耦、相位调整等。针对一类带有旋转部件的机械臂，Yamanaka［10－11］分析了端部带有转子的均质梁的动力学和稳定性问题，其转子转轴沿梁的轴向。Li［12］等研究了端部带有任意方向旋转轴的转子的柔性连接的稳定性问题。

国内外关于陀螺效应对机翼或飞机颤振特性的影响机理研究文献较少。在实践中常根据经验将陀螺效应等效成一定的系统阻尼，在ω法或p－k法计算时采用阻尼矩阵计入陀螺效应进行颤振计算［1］，取得较好的效果。尽管陀螺力矩在形式上与系统速度有关，但其功率恒等于零，即其本身并不是阻尼力［13］，因此将陀螺效应等效成系统阻尼的方法缺少一定的理论支撑。王彬文［14］等用有限元方法研究了转子陀螺效应对带有翼吊发动机系统振动特性的影响。

本文从机翼结构动力学和转子动力学基本理论出发，建立了计及陀螺效应的机翼弯扭颤振方程，忽略发动机吊挂柔性等影响，分析了陀螺效应对系统颤振特性的影响规律，为进一步分析机翼－发动机系统颤振特性提供一定的理论依据。

1 颤振方程的建立

如图1（a）所示，将机翼－发动机系统简化为一端固支的弯扭耦合Bernoulli－Euler悬臂梁，忽略发动机与机翼间的连接刚度。机翼翼展为l，半弦长为b，右手坐标系o－xyz原点o位于机翼根部，ox轴与机翼刚轴重合，oy轴沿飞机航向。图1（b）所示为机翼变形后x＝x0处弦向截面示意图。o′为机翼刚轴与截面交点，截面位移为v、w，截面绕o′转角为θ。Cw为截面重心，沿弦向与刚轴距离为e。发动机重心位置Cs，坐标为（x0，y0，z0），发动机重量为 ms，转子转速为Ω，旋转矢量方向与刚轴垂直，来流速度为U∞。

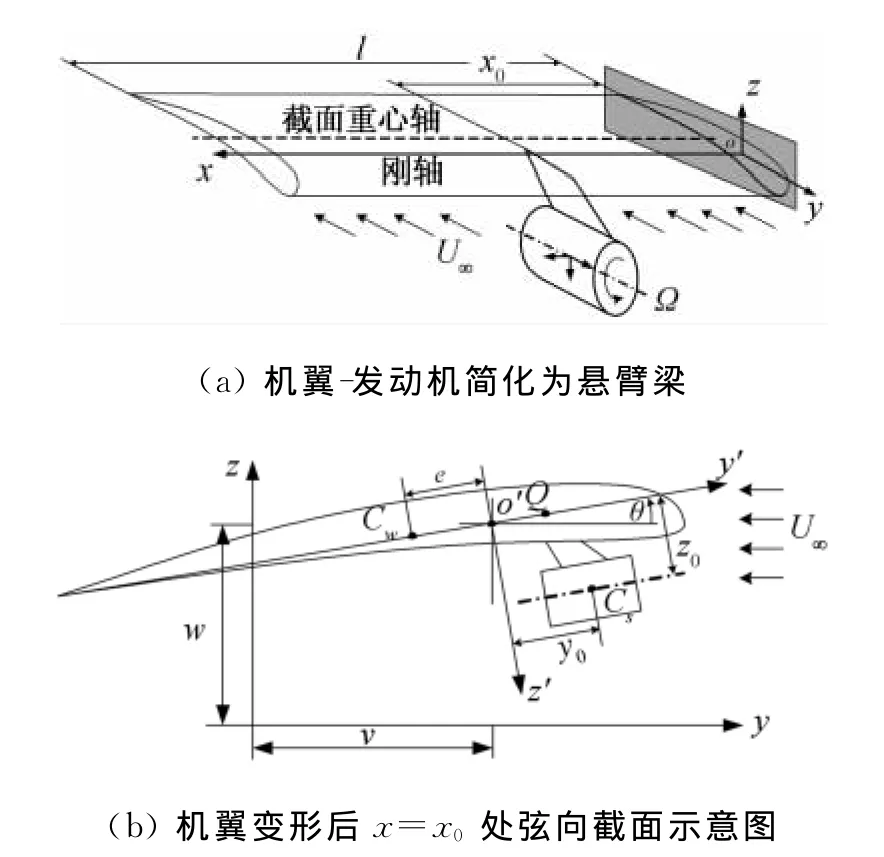
图1 机翼－发动机系统示意图Fig.1 Illustration of the Wing－Engine system

由Hamilton变分原理

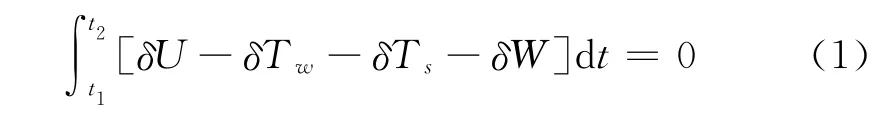
可推导得系统动力学方程，其中δU、δTw、δTs和δW分别为机翼势能、机翼动能、发动机动能和外力做功的变分。由弯扭耦合悬臂梁动力学分析，机翼势能的变分为：

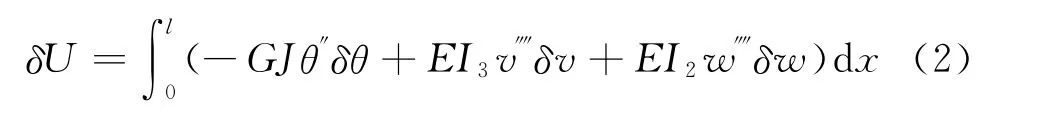
其中，EI2为梁的面外弯曲刚度，EI3为梁的面内弯曲刚度，GJ为梁的扭转刚度。

本文通过建立动车组单辆车整体称重模型，提出了3个调平指导参数以及高度调整阀调平条件。3个调平指导参数分别反映了影响动车组单辆车整体称重调平的3个独立因素：前转向架不平、后转向架不平以及车辆重心偏心。结合现场数据验证了高度调整阀调平条件的正确性。在此基础上可以利用调平指导参数来进行判断，并明确指出应在转向架加设垫片以满足调平条件。应用此称重调平规律和3个调平指导参数以及高度调整法调平条件来指导车辆现场称重，可以有效避免工人的盲目操作，显著提高车辆现场称重效率，还为计算机编写计算动车组单辆车整体称重调平程序提供了必要的理论支持，同时也为车辆称重调平的数字化、智能化提供指导方向。

机翼动能的变分可表示为

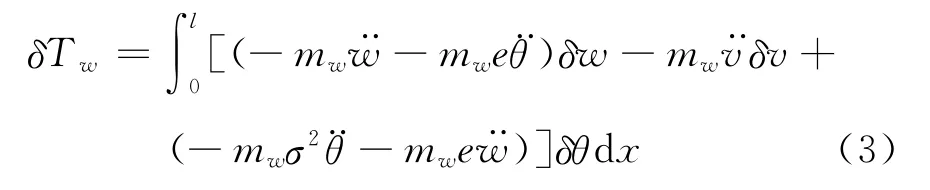
其中，mw为机翼单位长度质量，e为机翼截面重心与刚轴的距离（重心在刚轴前为正），σ为机翼单位长度截面绕刚轴的惯性半径。

对发动机动能分析可知，发动机的动能的变分由两部分组成，δTs＝δTm＋δTr，其中δTm为发动机集总质量的动能的变分，δTr为发动机转子的转动动能的变分。

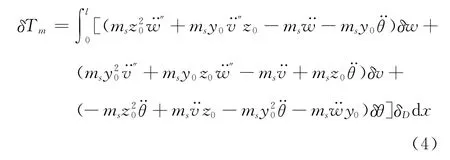
δD＝Dirac（x0－x）。当机翼变形时，向量Ω的偏转角在oxy和oyz平面的投影分别为v′和θ，由转子动力学理论可知，发动机转子的转动的动能可表示为：

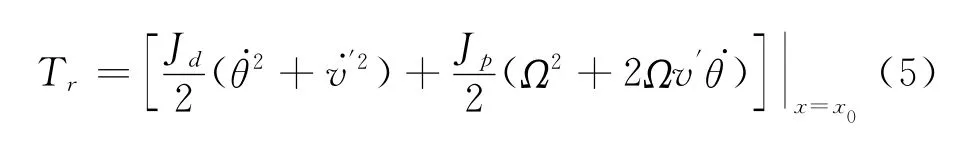
其中，Jp为转子绕其转轴的极转动惯量，Jd为转子的赤道转动惯量。对Tr求变分可得：

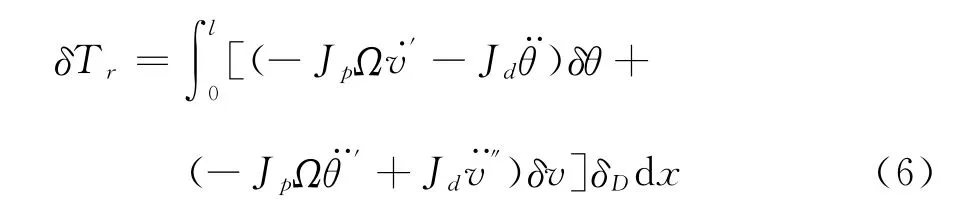
非定常气动力做虚功为：

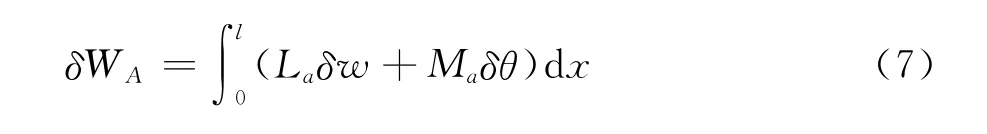
其中，La和Ma分别为气动升力和力矩，根据Theodorsen非定常气动力理论：

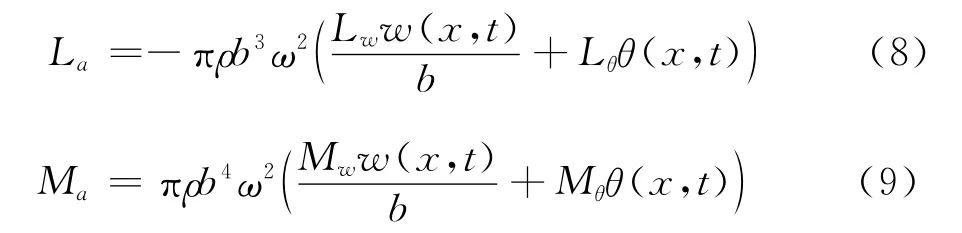
Lw、Lθ、Mw和Mθ为气动系数［15］。

将式（2）～（4）和（6）、（7）代入式（1）可得如下计及发动机转子效应的动力学方程：

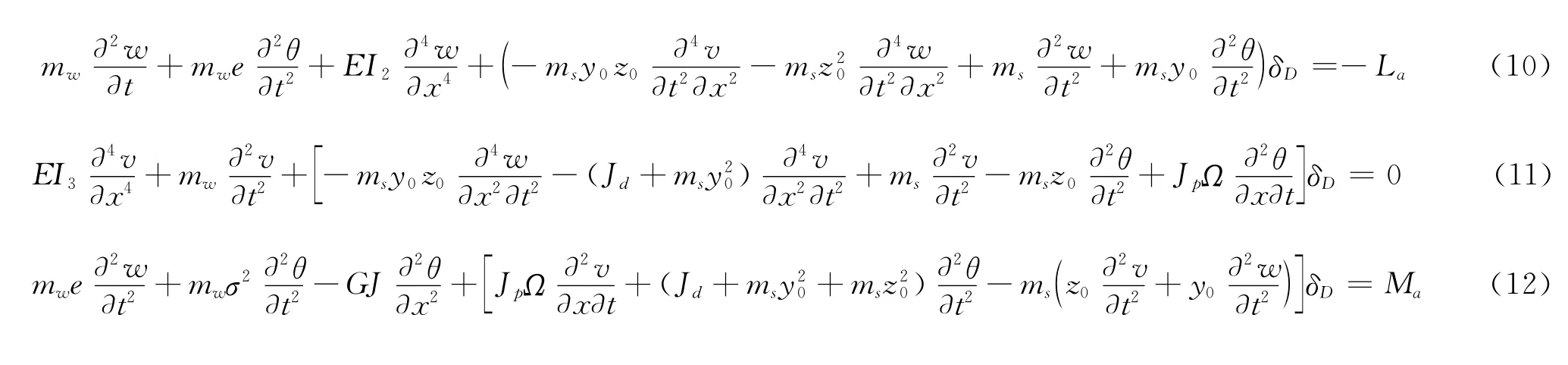
本文采用extended Galerkin［16］对上述系统动力学方程进行离散化并求解颤振特性，该方法仅需基函数满足几何边界条件的要求，而将自然边界条件包含在控制方程中。因此，令

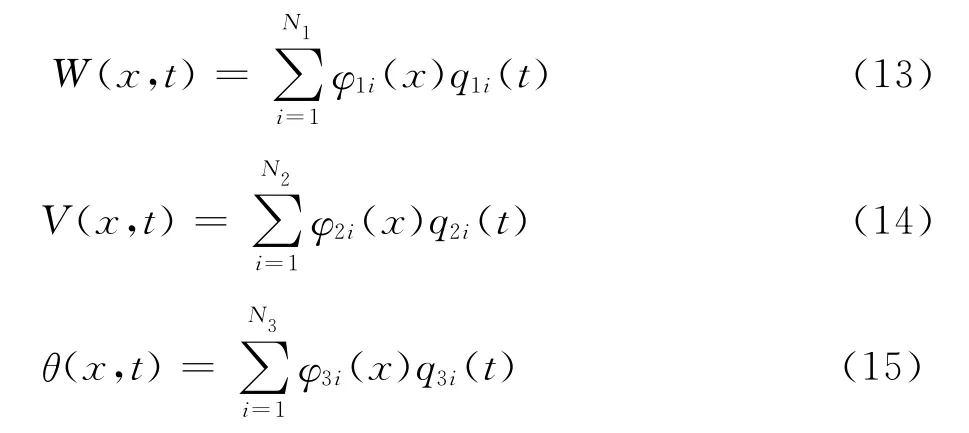
选取如下满足几何边界条件的函数作为基函数：

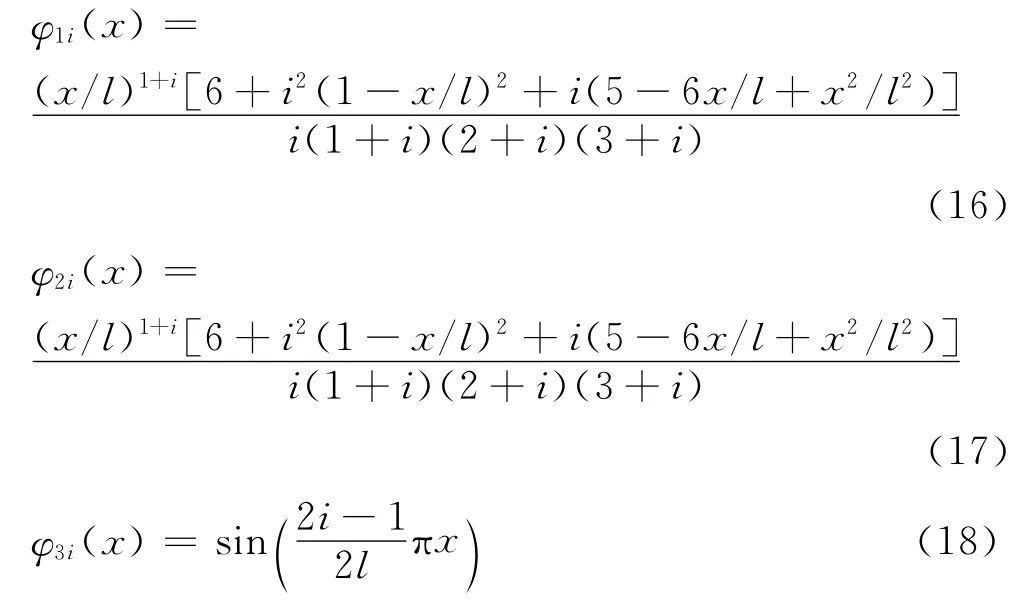
代入方程（10）～（12），积分可得离散后的系统颤振方程：

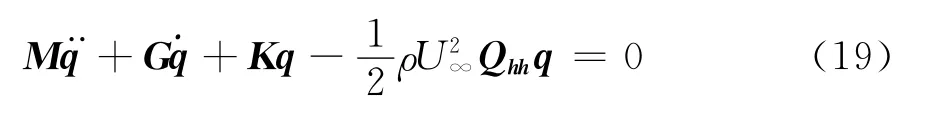
其中q＝｛q11，…，q1N1，q21，…，q2N2，q31，…，q3N3｝T，质量矩阵M为对称正定矩阵，刚度矩阵K、气动力矩阵Qhh为对称矩阵，由于系统陀螺力项与和相关，陀螺矩阵G为非对称矩阵。对系统动力学方程（19）运用p－k法可求得系统的颤振特性。

2 算例分析

采用Runyan机翼模型［17］结构参数，对系统颤振特性进行分析，各主要参数如下：l＝1.2192m，b＝0.1016m，EI2＝403.76N·m2，EI3＝403.76N·m2，GJ＝198.76N·m2，mw＝1.2942kg·m－1，ms＝1.578kg，ρ＝1.224kg·m－3，σ＝0.053m，Jp＝0.01kg·m2，Jd＝0.0185kg·m2。定义无量纲惯性矩用以表征转子惯性矩与梁结构刚度、质量的相对大小，式中图2所示为发动机转速Ω＝0rpm时，发动机位于不同机翼展向位置x0／l时的系统弯扭颤振速度和颤振频率，图中同时给出了文献［17］的试验结果，从图可以看出，采用本文简化模型计算得到的结果与文献中结果吻合得较好。

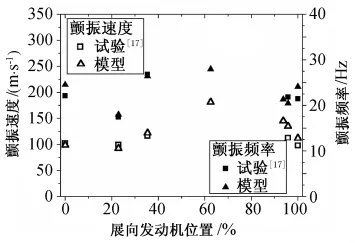
图2 Ω＝0rpm时发动机不同展向位置的系统颤振速度和颤振频率Fig.2 Flutter speeds and frequencies of the system with different spanwise locations andΩ＝0rpm

如图3所示为发动机转子转速发动机位于机翼展向位置x0／l＝22.9%且Ω＝0rpm（即没有陀螺效应作用）时系统颤振V－g、V－ω图。当Ω＝0rpm，系统弯扭颤振速度为91.18m／s，颤振频率为18.17Hz。当计及发动机陀螺效应时，在陀螺力矩的作用下系统固有频率和固有振型发生变化，如图4所示为系统固有频率随发动机转速（无量纲惯性矩）变化的Campbell图。根据陀螺力矩理论，结合系统结构特点可知，转子转动方向随着机翼结构振动而变化，陀螺力矩作用在机翼面内弯曲运动和扭转运动方向，从而使得涉及上述两运动的系统模态相互耦合。

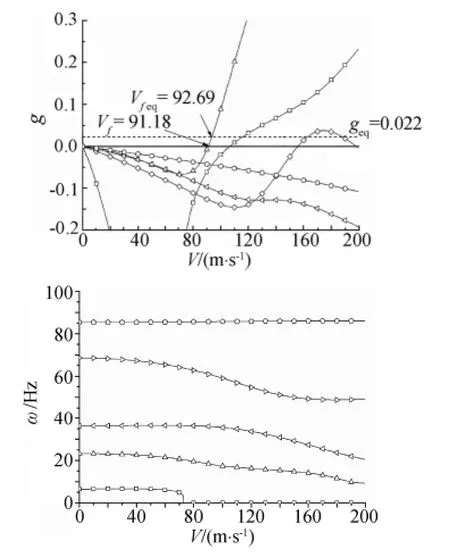
图3 x0／l＝22.9%、Ω＝0rpm时的V－g图和V－ω 图Fig.3 V－gand V－ω graph of the system with x0／l＝22.9%andΩ＝0rpm

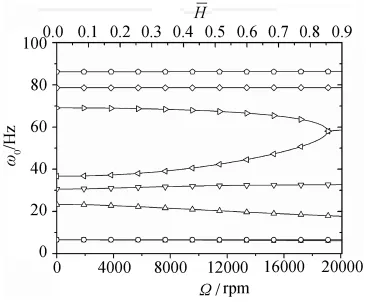
图4 系统固有频率Campbell图Fig.4 Campbell diagram of the system natrual frequencies

陀螺效应对系统固有特性的耦合效应将进一步影响其颤振特性。如图5所示为系统颤振特性随发动机转速变化曲线，由图可知，随着发动机转速的提高，系统颤振速度和颤振频率都逐渐增大。

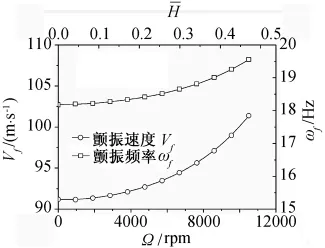
图5 发动机转速对系统颤振速度和颤振频率的影响曲线Fig.5 Influence of gyro effects on the flutter velocity and frequency

进一步考察Ω＝5730rpm（¯H＝0.257）时系统的颤振特性，其颤振V－g、V－ω图如图6所示，此时颤振速度为92.96m／s，颤振频率为18.52Hz。对比图3和图6可知，当不考虑系统吊挂刚度时，在陀螺效应作用下，机翼－发动机系统的V－g、V－ω图基本相似，即系统颤振发生机理未发生根本性变化，因此，发动机陀螺效应可等效成一定的系统结构阻尼geq。等效阻尼可由如下方法计算：设在一定的发动机转速下系统颤振速度为Vf，在不计陀螺效应时系统颤振V－g曲线的相应颤振模态分支上空速为Vf时对应的阻尼比即为该转速所对应的等效阻尼。

根据上述等效阻尼的定义及计算方法可得Ω＝5730rpm（¯H＝0.257）时，转子陀螺效应等效阻尼为geq＝0.022，如图3中水平虚线所示。图7给出了系统等效阻尼随着发动机转速提高的变化曲线。由图可知，等效阻尼亦随着发动机转速的增加呈抛物线型增大。

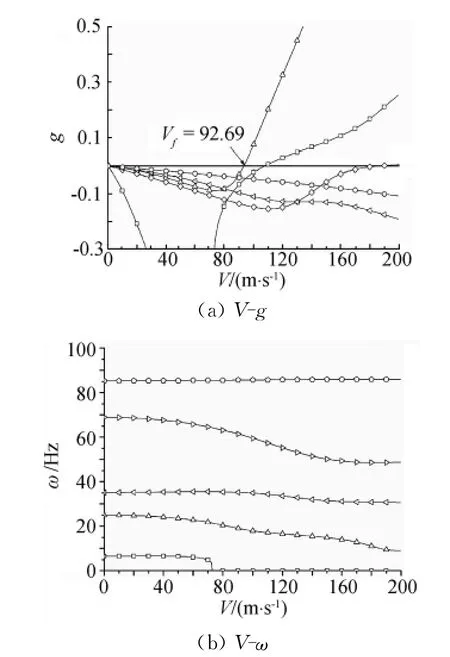
图6 x0／l＝22.9%、＝5730rpm时的V－g图和V－ω 图Fig.6 V－gand V－ω graph of the system with x0／l＝22.9%andΩ＝5730rpm

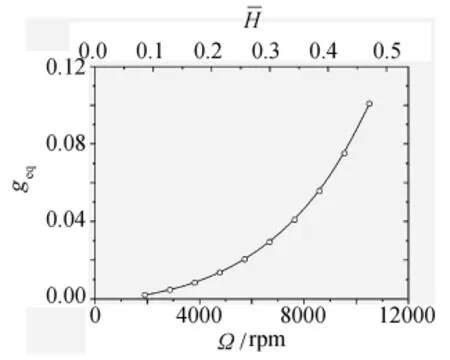
图7 转子效应等效阻尼曲Fig.7 Curve of the gyroscopic equivalent damping

3 结 论

本文通过建立计及发动机转子陀螺效应的机翼弯扭颤振分析方程，在不考虑发动机吊挂刚度的条件下，通过分析得到如下结论：

（1）在发动机转子陀螺效应的作用下，机翼弯扭型颤振速度和颤振频率随转子转速的增加而增大，且发动机转子陀螺效应不影响机翼颤振形式；

（2）尽管陀螺力矩本身并非阻尼力，但由于其在机翼颤振特性中具有上述特点，仍可以将其对机翼颤振特性的影响等效成一定的系统阻尼，且该等效阻尼随着发动机转速的增加而增大。

［1］管德.飞机气动弹性力学手册［M］.航空工业出版社，1994.

［2］D′ELEUTERIO G M T.On the theory of gyroelasticity［J］.Journal of Applied Mechanics，Transactions ASME，1988，55（2）：488－489.

［3］D′ELEUTERIO G M T，HUGHES P C.Dynamics of gyroelastic spacecraft［J］.Journal of Guidance，Control，and Dynamics，1987，10（4）：401－405.

［4］D′ELEUTERIO G M T，HUGHES P C.General motion of gyroelastic vehicles in terms of constrained modes［C］.AIAA／ASME／ASCE／AHS 26th Structures，Structural Dynamics and Materials Conference.1985，384－390.

［5］D′ELEUTERIO G M T，HUGHES P C.Dynamics of gyroelastic continua［J］.Journal of Applied Mechanics，Transactions ASME，1984，51（2）：415－422.

［6］D′ELEUTERIO G M T.Dynamics of gyroelastic vehicles［R］.UTIAS Report（University of Toronto，Institute for Aerospace Studies），1986.

［7］HUGHES P C，D′ELEUTERIO G M T.Modal parameter analysis of gyroelastic continua［J］.Journal of Applied Mechanics，1986，53（4）：918－924.

［8］PECK M A，CAVENDER A R.Structural tuning through embedded angular momentum［A］.44th AIAA／ASME／ASCE／AHS／ASC Structures，Structural Dynamics，and Materials Conference［C］，2003，2：1462－1469.

［9］PECK M A，CAVENDER A R.Practicable gyroelastic technology［A］.27th Annual AAS Rocky Mountain Guidance and Control Conference［C］，2004，118：239－253.

［10］YAMANAKA K，HEPPLER G R，HUSEYIN K.On the dynamics and stability of a beam with a tip rotor［A］.The 35th AIAA／ASME／ASCE／AHS／ASC Structures，Structural Dynamics，and Materials Conference［C］，1994，2 1031－1038.

［11］YAMANAKA K，HEPPLER G R，HUSEYIN K.Stability of gyroelastic beams［J］.AIAA Journal，1996，34（6）：1270－1278.

［12］LI L，HEPPLER G R，HUSEYIN K.Stability of a flexible link with an arbitrarily oriented tip rotor and a conservative tip load［C］.IEEE Interational Conference on Robotics and Automation.2000，2：1472－1477.

［13］陈予恕，曹登庆，黄文虎.近代机械非线性动力学与优化设计技术的若干问题［J］.机械工程学报，2007，43（011）：17－26.

［14］王彬文，孙侠生，齐丕骞.转子陀螺效应对系统振动特性的影响［J］.振动工程学报，2010，23（增刊）：63－67.

［15］HODGES D H，PIERCE G A.Introduction to structural dynamics and aeroelasticity［M］.Cambridge：Cambridge University Press，2002.

［16］FLETCHER C.Computational Galerkin methods［M］.New York：Springer－Verlag，1984.

［17］RUNYAN H，WATKINS C.Flutter of a uniform wing with an arbitrarily placed mass according to a differential－equation analysis and a comparison with experiment［R］.NACA Rep.1848，1950.