一种用于分离流动的网格自适应算法

韩志熔，陆志良，郭同庆，陈迎春，2

（1.南京航空航天大学 航空宇航学院，江苏 南京210016；2.上海飞机设计研究院，上海200232）

0 引 言

网格生成及自适应在数值分析中起着重要的作用。在大量的工程问题中，会遇到在非常狭小的区域内，某些物理量却发生剧烈变化的情况。这个问题给数学处理造成很大的困难。采用均匀网格对这样的问题求解将难以获得合理的精度。网格自适应方法是解决这类问题的一个有效途径。

目前的网格自适应方法主要针对无粘流动问题［1］。在粘性流动情况下，针对不可压N－S方程，一些有限元自适应方法也取得了进展［2－3］。而对于可压缩粘性流动问题的自适应研究近年来正成为热点［1，4］。

本文对于这一问题的研究主要是以下两个部分：（1）自适应指示函数的确定；（2）网格密度改变的方法。针对第一个问题，本文提出了利用单元速度紊乱度作为指示变量构造网格自适应指示函数。围绕第二个问题，采用H型网格自适应方法，提高局部网格密度。

1 自适应网格技术

1.1 指示变量与指示函数

可压粘性流场中，精确捕捉附面层，分离涡，湍流区等是非常重要的。在这些区域，温度、速度的梯度可能较大，会对整个流场的精确求解产生较大影响。因而本文主要着重于对粘性流场中边界层、湍流区域和涡结构的捕捉。分析边界层、湍流区域和涡结构的流场，知道由于粘性迟滞的作用，附面层内的速度相对于自由来流速度比较小；涡结构中的速度沿半径自边缘向涡核中心递减；湍流区域内速度主要表现为方向异性与速度的脉动。基于上述事实，本文提出利用单元流场速度的紊乱度获得自适应指示变量vN：

其中VN是第N个单元的流场速度，V∞是自由来流的速度。同时构造自适应指示函数｜vN－1｜。此指示函数可以同时捕捉附面层、湍流区域及涡。在这些关键区域内VN·V∞值会小于V∞·V∞值，甚至在数值上会出现符号相反的情况。所以当方程（1）的值小于α时（0＜α＜1），｜vN－1｜会大于1－α，VN·V∞与V∞·V∞数值上符号相反时，｜vN－1｜更会大于1。这样会方便我们给出一个阀值Vthreshold。遍历所有单元并记录指示函数｜vN－1｜值，当其大于给定的阀值Vthreshold时，将第N个单元标记为需要加密的单元，Vthreshold的经验值为0.1～0.3。

1.2 H型网格自适应方法

目前网格的自适应通常可通过2种途径来实现，一种是向初始网格中插入新的网格单元从而提高单元密度的H型自适应网格技术［5］；另一种是在保持网格单元总数不变的情况下，通过移动网格结点的位置来改变网格单元密度的分布的R型自适应网格技术［6］。

在流动马赫数比较小时，应用R型网格自适应方法后，网格点的移动不明显，流场数值计算结果提高不显著。H型技术可以有效解决这个问题。但是对于结构网格，如果局部插入网格结点会破坏原有的拓扑结构产生悬挂点，如图1所示。

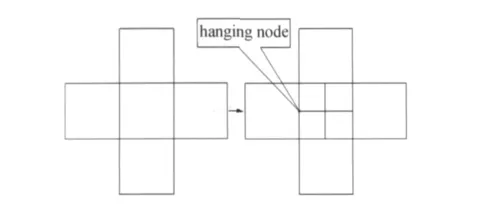
图1 悬挂点Fig.1 Hanging node

这使得结构网格求解器失效。为了解决这个问题，本文在计算中采用了以边为基础的非结构算法：迭代过程中按边的顺序循环，同时索取边的左右单元获取左右单元的流场变量，从而得到边的通量，并将左单元加上边的通量，右单元减去边的通量。所以按边循环完成后就同时获得了所有单元的通量。这样不但解决了悬挂点的问题，而且为我们今后推广到三维创造了条件。

1.3 自适应后网格的光顺

对整个流场的精确求解产生较大影响的区域内，仍然会有网格单元的指示函数值非常接近但低于阀值，这使得初步加密后的网格可能会出现不光顺的情况。图2给出了几种不光滑情况：未被标记的单元有三个相邻单元是被标记单元；未被标记的单元对边的两个相邻单元中，一个是被标记单元，另一个是物面边界，或者两个都是被标记单元。

网格不光滑处存在误差，可能会影响计算的稳定性，或者使得到的解不能正确反映流动特性。必须查找出不光滑网格单元并消除。

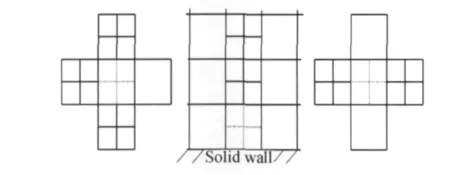
图2 不光滑网格单元Fig.2 Nonsmooth grid cells

网格自适应之后，其流场计算在原有流场的基础上继续进行迭代计算。对新增加的网格单元，其流场变量值由此处的原有单元变量值插值得到，这样网格自适应之后，其流场计算在原有流场的基础上继续进行迭代计算，节约了计算时间。

2 控制方程

定义Ω是流场中任意一个空间位置固定的控制体，∂Ω是Ω的边界，dS是∂Ω上的面元。守恒型N－S方程在Ω内积分形式为：

x－z平面二维坐标下的守恒变量表达式为W＝［ρρuρwρE］T，Fc、Fv分别表示积分形式下的对流通量与粘性通量。湍流模型选取SA一方程模型。

本文选取Jameson中心格式有限体积法进行空间离散，采用五步Runge－Kutta时间推进法求解定常N－S方程，采用双时间推进法求解非定常N－S方程。

3 算例

本文将给出二维NACA0012翼型静态绕流与动态绕流两个算例。

算例1

流场条件取马赫数Ma＝0.15，雷诺数Re＝0.5×106并采用C型网格，如图3（a）所示，单元数为192×46。在初始网格的基础上进行流场迭代计算，依据所得流场解应用网格自适应技术，之后在原流场的基础上继续迭代计算。随着各个计算状态迎角的不同，需要加密的网格数目也不同。如图3（b）、3（c）所示，迎角分别是α＝5.05°以及α＝12.07°时自适应后的网格。

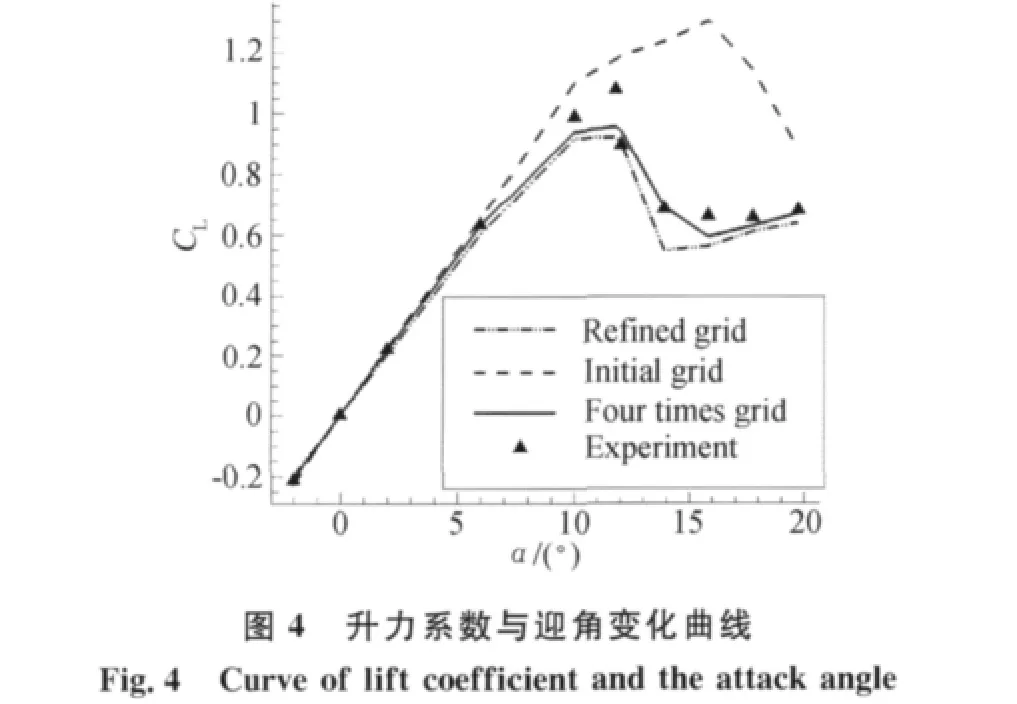
同时在初始网格的基础上，将所有单元一分为四，即单元数为384×92，并计算得到升力系数CL值。如图4所示，将不同网格数下计算所得升力系数CL值与实验值［7］比较，来流迎角小于10°时吻合都比较好，但在10°之后采用初始网格计算所得升力系数与试验值偏差较大。而采用自适应网格与四倍网格计算所得升力系数与试验值误差较小。

在所有计算状态中网格数目最多的一次增加了7137个单元。相对将所有单元一分为四，单元数目增加量为35328个的情况而言，单元增加很少但计算结果却差别不大。

算例2

迎角变化规律为：α＝6.25°±8.5°×（2kt＊）

其中减缩频率k＝0.075，无量纲化时间t＊＝t×U∞／c。来流马赫数Ma＝0.4，雷诺数Re＝3.4×106。初始网格为C型贴体网格，单元数为192×35。在迎角达到最大值时加入网格自适应，自适应后网格如图5所示，网格节点增加了7060个，网格单元增加了6879个。

图5 （a）初始C型网格，（b）自适应后的网格Fig.5 （a）Initial C－type grid，（b）Refined grid

文献［8］给出了流动实验测量结果。图6对初始网格下的计算结果，自适应网格下的计算结果与实验值进行了比较。从图中可以看出，在最大迎角附近，采用网格自适应所得到的计算结果相对初始网格所得到的计算精度有明显提高。

图6 NCA0012翼型轻度失速下的（a）升力系数、（b）力矩系数迟滞环Fig.6 （a）Lift and（b）Momentum coefficient hysteresis for dynamic light stall around NACA0012

4 结 论

本文对二维可压缩粘性流动问题下的自适应技术进行了探讨与应用。提出利用流场速度的紊乱度作为指示函数的变量，同时捕捉附面层，湍流区域以及涡结构。对NACA0012翼型的一些典型分离、失速的算例进行了网格自适应数值计算，并与初始网格计算结果以及实验结果进行了比较。对比结果显示采用本文提出的判据进行网格自适应，能够在增加少量的网格单元数量的情况下明显提高计算的精度。

［1］JIN CHANG－QIU，XU KUN.An adaptive grid method for two－dimensional viscous flows［J］.JournalofComputationalPhysics，2006，218（1）：68－81.

［2］DI Y，LI R，TANG T，et al.Moving mesh finite element methods for incompressible Navier－Stokes equations［J］.SiamJournalonScientificComputing，2005，26（3）：1036－1056.

［3］PEROT B，NALLAPATI R.A moving unstructured staggered mesh method for the simulation of incompressible free－surface flows［J］.JournalofComputationalPhysics，2003，184（1）：192－214.

［4］ONKAR SAHNI，KENNETH E JANSEN，MARK S SHEPHARD，et al.Adaptive boundary layer meshing for viscous flow simulations［J］.Engineeringwith Computers，2008，24（3）：267－285.

［5］HEUVELINE V，SCHIEWECK F.H1－interpolation on quadrilateral and hexahedral meshes with hanging nodes［J］.Computing，2007，80（3）：203－220.

［6］陈宣友，董海涛，李椿萱，等.3点逐步r型自适应网格算法［J］.北京航空航天大学学报，2006，32（1）：13－17.

［7］CHRIS C CHRITZOS，HARRY H HAYSON，ROBERT W BOSWINKLE.Aerodynamic characteristics of NACA0012airfoil section at angles of attack from 0deg to 180deg［R］.NACA，Technical Note 3361，1955.

［8］MICHAEL KERHO.Adaptive airfoil dynamic stall control［J］.JournalofAircraft，2007，44（4）：1350－1360.