超声速高度欠膨胀冲击射流的大涡模拟

刘 海，姚朝晖

（清华大学 航天航空学院，北京100084）

0 引 言

欠膨胀超声速冲击射流在许多工程技术领域得到广泛的应用，如STOVL（Short Take Off and Vertical Landing）飞行器起飞和着陆、火箭的发射，以及除尘、除水等工程问题；而且其流场结构复杂，激波和涡之间存在着强烈的相互作用。因此无论是工程应用还是基础研究，冲击射流都极具研究价值［1－3］。

Alvi［1］等通过实验给出了不同工况下的流场阴影图和壁面上的压强分布曲线，并指出冲击平板上的压强脉动的主频与冲击单音的频率相同。姚朝晖等［3］利用纹影和高速摄影技术发现在马赫盘出现之前，冲击射流的流场是整体振荡的；而马赫盘出现之后，流场振荡局限于马赫盘与冲击平板之间。Henderson［4］讨论了在高度欠膨胀工况下流场的冲击单音的存在与马赫盘出现位置的关系，观察到了流场的环形激波的生成和消失，给出一些瞬时脉动流场的涡的信息，并对反馈环进行了新的论述。

图1为高度欠膨胀（来流总压p0跟环境压强pa的比值NPR大于3.8）冲击射流的流场示意图。由于RANS只能得到流场的平均场的信息，而相比实验LES可以获得更丰富的流场信息，所以本文使用大涡模拟对高度欠膨胀的超声速冲击射流的流场进行了数值模拟，主要是对流场的振荡、内外剪切层之间的环形激波的生成和消失过程以及内剪切层的涡结构的演化进行了仔细的研究。

图1 高度欠膨胀冲击射流流场示意图Fig.1 A schematic of the highly underexpanded supersonic impinging jet

1 数值模拟方法

首先对柱坐标系下的三维可压缩非定常NS方程进行基于密度的加权过滤［5］：

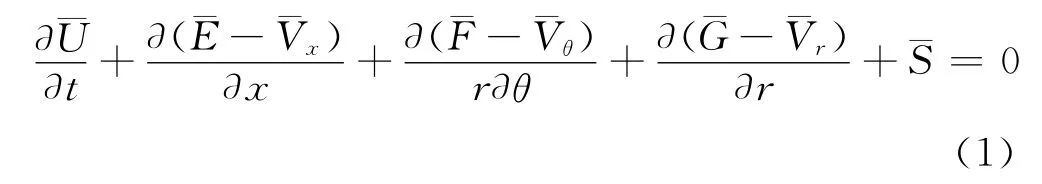
其中，x、θ、r分别表示的是轴向、周向和径向坐标，各项参数如下：

式中τ表示指分子粘性项，而σ和Q则代表过滤产生的亚格子应力和亚格子热通量项。

由于方程无量纲化参考的是环境流场和喷嘴出口直径，所以气体的状态方程为：

粘性系数的计算采用Sutherland公式：

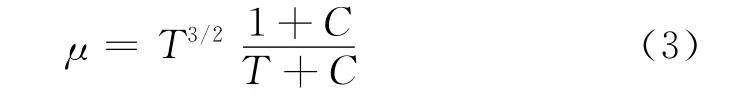
对于空气，C＝110.4／Ta，Ta为环境温度。

本文的亚格子应力模式采用的是Smagorinsky模型：

式中Prt为湍流普朗特数，而涡粘系数的计算公式为：

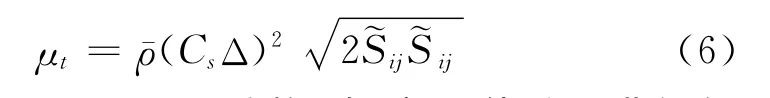
式中Cs为Smagorinsky系数，在壁面附近再进行如下的修正：

计算中对流项采用五阶WENO格式进行离散，粘性通量项采用显式的4阶中心格式进行离散。时间积分采用四步三阶具有强稳定保持性质的Rung－Kutta格式［6］，其CFL数等于2，所以计算效率较高。并对计算程序进行了并行化。

本文在计算取喷嘴出口为临界声速来流条件；出口和远场边界取与时间相关的无反射边界条件［7］；冲击壁面和喷嘴壁面取绝热无滑移固壁边界条件；中心轴在柱坐标系下为奇轴，为保证速度在轴线上单值，采用Lele基于级数展开得到的公式进行插值［8］。

2 程序验证

本文程序验证所用的算例与Alvi的实验工况［1］相同：其中收缩喷嘴的出口直径为d＝25.4mm，冲击距离h／d＝2.0，来流总压跟环境压强的比值NPR＝2.5，冲击平板是大平板。计算网格数：x×θ×r＝300×48×250。本文程序有效性的验证主要是将平均场的数据结果和实验进行对比。

观察图3、图4可以发现本程序计算得到的流场的激波栅格结构的大小和位置以及冲击壁面上的压强系数（Cp＝（p－pa）／（p0－pa））分布与实验结果吻合较好。从而验证了程序可以有效地模拟超声速冲击射流的流场。

3 流场的振荡

下面讨论的算例是基于Henderson［4］的实验工况：喷嘴直径d＝25.4mm，冲击距离h／d＝2.08，喷嘴唇厚0.1d，压比NPR＝4.03，冲击平板为大平板。计算网格数为：x×θ×r＝300×48×250。此种工况流场为对称模态，所以后文分析主要是基于θ＝0的平面进行的，图中r／d＝0对应于计算域的中心轴线。

由图5的马赫数分布可以看出马赫盘及斜激波向流场下游运动的时候，斜激波后面的流场的亚声速区域逐渐增大，同时马赫盘后面的流场的速度也在减小，而马赫盘往上游运动时斜激波和马赫盘后的流场变化趋势相反。原因是当马赫盘向下游运动的时候，马赫盘前面的流场膨胀区域变大，所以气体会进一步膨胀，马赫盘前的马赫数提高，所以马赫盘的激波强度变大，导致马赫盘后面的流场速度减小。同时随着马赫盘往下游运动，斜激波的激波角度变大，所以斜激波强度也变大。马赫盘在向下游运动时，可以发现马赫盘的直径有减小的趋势。

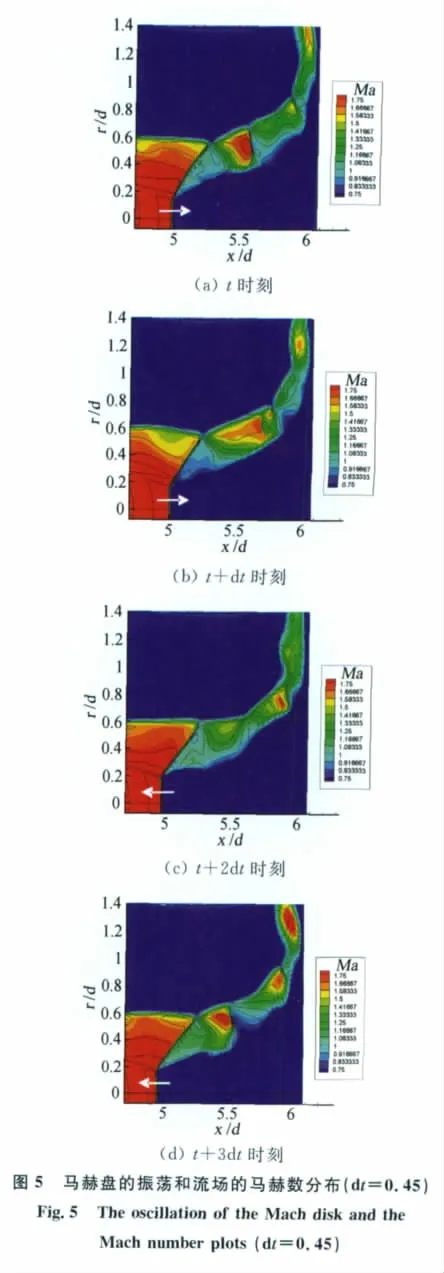
4 环形激波的生成与消失

图6对计算和实验的瞬时流场进行了简单的对比，可以看出流场的马赫盘，斜激波和环形激波的形状基本一致。在Henderson的实验阴影图中，由于冲击壁面附近的图像不清晰，在内外剪切层之间只观察到一道环形激波，而计算中观察到两道环形激波的生成与消失的周期过程。

图6 数值计算的密度云图和实验阴影图Fig.6 Computed density contour and measured shadowgraph photograph

图7为密度等值线和旋转强度云图，由图7（a）可见在马赫盘后面有两道环形激波a和b存在于流场的内外剪切层之间，在剪切层上存在着大尺度涡结构，此时马赫盘往下游运动；图7（b）中涡结构A、D追上环形激波a一起向下游运动，而此时激波a和激波b强度变弱；图7（c）中可看出激波b已经消失，激波a下行过程中在靠近它的地方开始有新环形激波bb生成，环形激波a进一步变弱；在图7（d）中环形激波a消失，在斜激波后面形成新的环形激波aa，而激波bb随大尺度涡结构A、D在往下游运动的过程中逐渐变强。

斜激波后第一道环形激波形成后在内外剪切层的大尺度涡结构追上它之前强度逐渐变强，而两个涡结构追上它一起下行过程中则逐渐变弱，消失前在靠近它的附近生成一道新的环形激波，新的环形激波会随大尺度涡下行过程中先增强然后变弱消失。同时可以发现环形激波生成与消失的周期、大尺度涡结构周期和马赫盘的振荡周期一致。

5 内剪切层的涡

Henderson在实验结果中给出了流场的脉动场，此处本文对流场的内剪切层的涡结构的演化进行进一步的讨论。

由于流场运动的周期性，所以首先看图8的最后两个图8（d）和（e）然后接着再看图（a），马赫盘由向右运动变成了向左运动，相比其它时刻的图，可见在马赫盘与斜激波的交点处，图8（e）中一个相对较大的涡结构开始卷起。即在马赫盘与斜激波相交的地方，当马赫盘运动到最下游时，内剪切层上一个相对较大的涡结构开始卷起，然后在下行过程中发展成大尺度涡结构，如图8中的涡B。

图8 内剪切层的涡结构演化（dt＝0.225）Fig.8 The evolution of the vortex（dt＝0.225）

对于图8中的涡结构A，与第二道环形激波一起下行，在到达冲击壁面时与壁面作用然后破碎，所有这些破碎的涡结构我们用A′表示，其中破碎的涡结构大部分随壁射流沿径向流出，小部分向回流区运动。由于涡A破碎成A′时，此时内外剪切层间的第二道环形激波靠近冲击壁面，在环形激波和冲击壁面之间形成高压区，使得破碎的涡结构沿射流壁面的径向运动受阻，会在原地打转一段时间，其中一部分破碎涡跟随回流往中心区移动。随着时间的发展，靠近壁面的环形激波会慢慢变弱消失，高压区消失，这些破碎的涡结构大部分将跟随着壁射流沿径向运动。

在图8的壁射流区，可以观察到在内外剪切层的作用下形成了壁射流区内外交错的涡结构序列。

6 结 论

基于柱坐标系下的NS方程，利用大涡模拟的方法创建了求解超声速冲击射流的三维并行计算程序，验证了程序的有效性。

对所模拟的高度欠膨胀冲击射流算例，在斜激波、马赫盘及涡结构的共同作用下，内外剪切层之间的环形激波存在着周期性的生成和消失过程。环形激波的周期过程与大尺度涡运动、马赫盘振荡周期一致。

内剪切层上的大尺度涡结构的形成与马赫盘和斜激波的振荡相关；环形激波与冲击壁面之间的高压会对内剪切层的涡沿径向运动形成一定的阻碍，内外剪切层的作用形成了壁射流区内外交错的涡结构。

［1］ALVI F S，LADD J A.Experimental and numerical investigation of supersonic impinging jets［R］.AIAA Paper 2000－2224，2000.

［2］ALVI F S，IYER K G.Mean ＆unsteady flow properties of supersonic impinging jets with lift plates［R］.AIAA Paper 99－1829，1999.

［3］姚朝晖，何枫，韩标，等.高速冲击射流流场特性与噪声机理的研究［J］.流体力学实验与测量，2003，17（2）：84－87.

［4］HENDERSON B，BRIDGES J，WERNET M.Experimental study of the oscillatory flow structure of tone producing supersonic impinging jets［J］.J.Fluid Mech.，2005，542：115－137.

［5］张兆顺，崔桂香，许春晓.湍流大涡数值模拟的理论与应用［M］.北京：清华大学出版社，2009：120－134.

［6］RUUTH S J，SPITERI R J.High－order strong－stability－preserving Runge－Kutta methods with downwind－biased spatial discretizations［J］.SIAMJournalofNumericalAnalysis，2004，42（3）：974－996.

［7］张涵信，沈孟育.计算流体力学－差分方法的原理和应用［M］.北京：国防工业出版社，2003：313－341.

［8］MORINISHI Y，VASILYEV OV，OGI T.Fully conservative finite difference scheme in cylindrical coordinates for incompressible flow simulations［J］.Journal ofComputationalPhysics，2004，197：686－71.