番薯片薄层热风对流干燥模型与传质性能

诸爱士，江飞燕

（浙江科技学院 生物与化学工程学院，杭州310023）

番薯，又名红薯等（学名Ipomoea batatas Lam.），整个热带和亚热带地区均有种植，主要生产地有中国、印度尼西亚、尼日利亚、乌干达和越南。中国番薯种植面积为106hm2左右，年总产量约1 500亿kg，种植面积和总产量均位居世界首位。近年来的研究表明，番薯营养丰富，是维生素A、维生素C及淀粉的极好来源，能量和膳食纤维含量高、低脂肪，也是β-胡萝卜素的重要来源［1］。但是由于鲜番薯含水量高，容易腐烂，又具有生产的季节性，因此考虑用比较适当的方法将番薯加工成干制品日益受到各国的重视，开发番薯系列产品在国际和国内都具有广阔的市场前景。

干燥能大大减少农产品的水分和微生物的活性，并最大限度地减少其在存储期间的物理和化学变化，提高了农产品质量的稳定性［2］。为了提高产量、保证质量的均匀性，工业干燥采用机械化生产。干燥是一个复杂的传热过程，期间不稳定的热量和水分传递同时发生［3-4］。从工程角度考虑，理解、掌握干燥过程动力学是重要的，所以数学模型被用于新干燥过程设计、现有干燥系统改进及干燥过程控制。已有许多数学模型被用来描述干燥过程，其中薄层干燥模型已被广泛使用［5-6］，已有许多中外文献［4-12］报道了对蔬菜、水果干燥特性和数学建模的实验研究，如苹果、胡萝卜、韭菜、杏子、银耳、白萝卜、南瓜和尖蜜拉等。然而报道番薯干燥动力学研究的数量有限，Diamante等［13］研究了空气温度、风速、湿度和番薯片厚度对干燥的影响，结果是用修正Page模型来描述番薯的干燥行为最好；Singh等［14］研究了空气的温度与焦亚硫酸钠和柠檬酸预处理对番薯片干燥动力学的影响，结果发现干燥过程中只有降速阶段，Page模型能很好地描述其干燥特性；Doymaz［15］研究了番薯在干燥柜中干燥的动力学，发现在5个模型中Logarithmic模型与实验数据拟合得最好；孟岳成等［16］研究了熟化后的红薯热风干燥特性及数学模型适用性。然而，在洞道式干燥器中番薯薄层热风对流干燥模型、有效水分扩散系数和活化能的研究鲜见报道。

本研究考察了干燥温度对干燥时间和速率的影响，用文献［4］报道的Newton、Henderson and Pabis、Logarithmic、Page、Modified page、Wang and Singh 6个模型拟合实验数据，以寻求适宜的模型，计算水分有效扩散系数和活化能。

1 材料与方法

1.1 试验材料

鲜番薯：肉淡桔红色，购于杭州农贸市场。经测定，其平均含水质量分数为81.7%（湿基），包装后储存于4℃的冰箱。用时将其取出，洗净，削去外皮，然后切片，外形尺寸为30mm×20mm×2mm。

1.2 试验仪器

DG100D数字型洞道干燥装置（浙江中控科教仪器设备有限公司），DHG-9123A型电热恒温鼓风干燥箱（上海精宏实验设备有限公司），BS124S型精密分析天平（北京赛多利斯仪器系统有限公司）。

1.3 试验方法

空气由离心风机提供，调节管路进口阀门控制好所需空气流量，由电加热器自动控制加热空气，使其温度至设定值；称取保湿的番薯片，要求各实验番薯片的用量基本相同，平铺一层盖满均匀分布小孔的干燥盘，放入洞道干燥机中进行干燥，废气不循环；按质量减量法连续记下干燥时间及与之对应显示的物料剩余质量，直至物料质量保持3min以上不变时，将物料连同物料盘从干燥机中取出，并将其迅速放入温度设置为105℃的电热恒温鼓风干燥箱，直至经称量质量保持不变，即可获得物料的绝干质量。

1.4 结果表达

1.4.1 干燥参数

基于绝干物料质量的含水质量分数Xt、瞬时的物料水分比MRt及瞬时干燥速率DRt，可分别按式（1）、式（2）及式（3）计算。

式（1）中：Xt—t时刻干基含水质量分数，无因次；mt— 物料t时刻的质量，g；mg—绝干时物料质量，g。

式（2）中：MRt—t时刻的水分比，无因次；X＊—平衡干基含水质量分数，无因次；X0—初始干基含水质量分数，无因次。

式（3）中：DRt—t时刻干燥速率，kg水／（kg干物质·s）；MRt＋dt—t＋dt时刻的水分比，无因次；t— 干燥时间，s。

1.4.2 模型检验指标

方程的决定系数R2值直接取自方程拟合时得到的数据，模型的相关系数r和残余方差S2分别按式（4）和式（5）［17］计算：

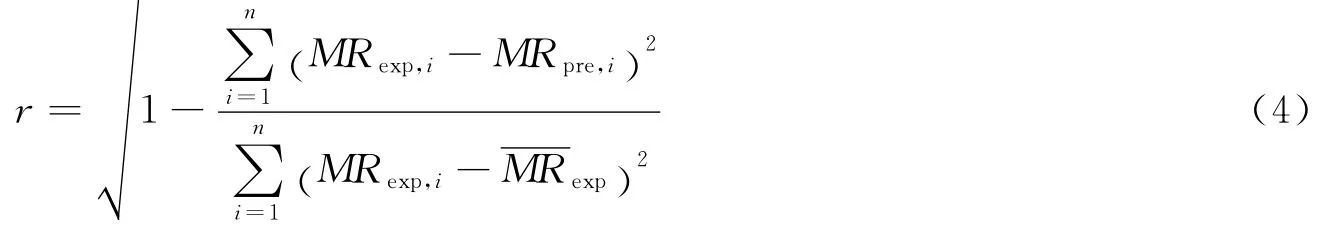
式（4）中：MRexp，i—MR 的实验值，无因次；MRpre，i—MR 的模型预测值，无因次；MRexp—MR的试验平均值，无因次；n—试验观察点数。

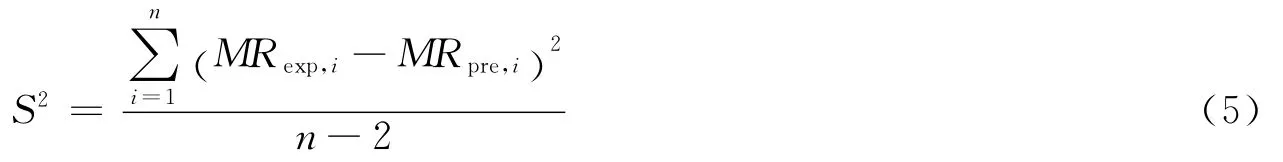
若某模型的R2与r值越与1相接近，或S2值越接近0，表明用该模型拟合试验数据，其拟合度越高。

1.4.3 扩散系数与活化能

物料在进行薄层干燥时，水分质量传递的参数——有效扩散系数Deff（m2／s），可用试验数据经菲克第二扩散方程式（6）求解［11，15］。

设恒定热风温度下Deff不变、物料各处的X0相同，忽略水分在物料外部的扩散阻力和物料因干燥所产生的体积收缩，式（6）应用于大面积片状物料的水分扩散时可视为一维扩散，其解为式（7）［18］。干燥时，由于片状试样的长与宽相对于厚度而言均比较大，故可将试样的水分传递简化为仅在试样厚度方向上的单向扩散，即一维扩散。

式（7）中：N—正整数；H—番薯片的厚度，m。

干燥盘有孔，试样平铺一层于盘上，试样上下双侧均可与热风进行对流传质，因此式（7）中H取试样厚度的一半。因干燥过程所需时间较长，故式（7）可简化为式（8）［4-5，11，15］。

将式（8）取对数，作lnMR ～t图，拟合直线，其斜率为-π2Deff／4 H2，因此可得Deff。

可由阿累尼乌斯方程（9）关联出Ea［11］。

式（9）中：D0— 阿累尼乌斯方程常数，m2／s；Ea— 活化能，J／mol；R— 气体摩尔常数，8.314J／（mol·K）；T—干燥空气温度，℃。

将式（9）取对数线性化，得到式（10）。

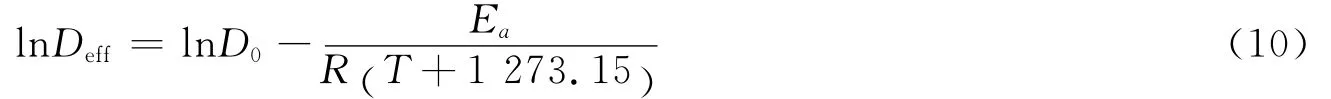
作lnDeff～1／（T＋273.15）图，拟合直线，得到斜率和截距，再分别计算出Ea和D0。

2 结果与分析

2.1 热风温度对干燥的影响

番薯片厚2mm，风速0.946m／s，装载量2.02kg／m2，研究了热风温度分别为60、65、70、75、80℃时的MR～t关系和DR～MR关系，分别见图1、图2。

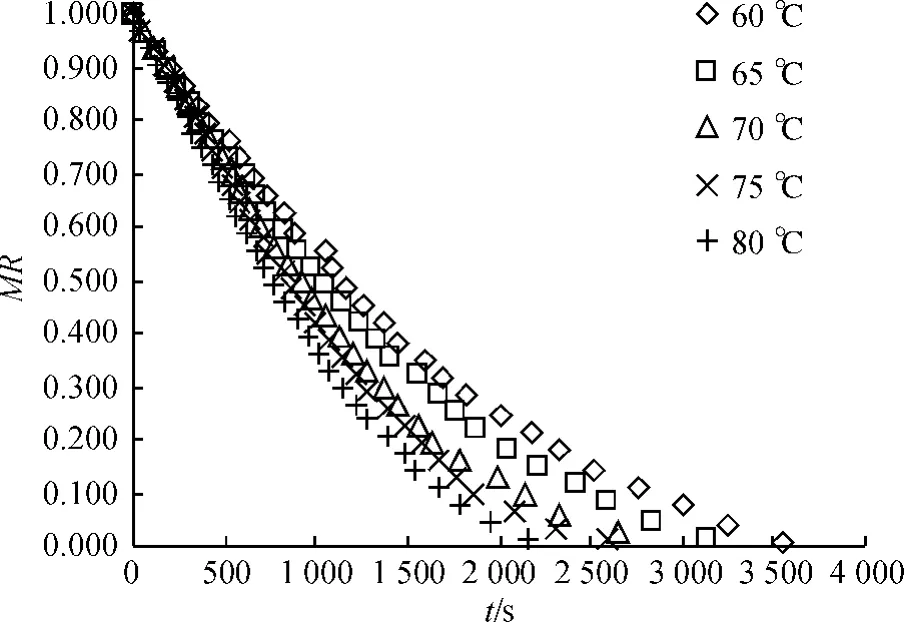
图1 不同干燥温度的MR～t关系Fig.1 Relation of MRand t at different temperatures

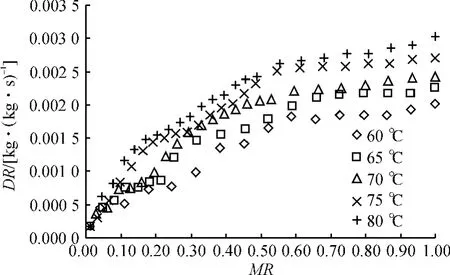
图2 不同干燥温度下的干燥速率曲线Fig.2 Rate of drying curves at different temperatures

图1 显示，水分比的变化与干燥温度变化呈对应关系；干燥时间变化趋势与干燥温度变化相反，即温度从60℃升高到80℃，水分比下降加快、干燥时间从3 548s缩短到2 164s。这是因为热空气温度越高，则空气与被干燥物料表面间的温度差越大，从而加大了传热推动力，能使传热速率加快；在进口空气湿度不变的情况下，升高热空气的温度，增大了其湿分的容量，从而降低了其相对湿度，增大了与物料的湿度差——传质推动力，加快了传质；干燥温度的升高也促进了水分子的热运动，加快了物料中水分的分子扩散；这些均说明了干燥介质温度对物料的干燥过程影响明显。

图2显示，干燥过程有一个预热段，速率下降，温度越高越明显，但较短。原因是干燥开始时物料温度低，与空气间的温差大，传热快使得传质也快，但随物料被加热，温差减小，干燥速率快速降低至恒速阶段。干燥有较长的恒速段，随温度升高恒速段变短；从60℃升高到80℃，平均干燥速率从0.001 8kg水／（kg干物质·s）增大到0.002 7kg水／（kg干物质·s）。干燥的降速阶段较长，每个温度下的速率下降幅度没有规律，但热风温度越高，相比降速时幅度较大。热空气与试样间的热量传递方式是对流传热，试样吸收热量温度升高后，水分以表面汽化方式传递给热空气，而试样内部的水分是在浓度梯度作用下以液态分子扩散的形式从内部扩散至试样表面。干燥初始，试样表面水分的性质与纯水相同，物料组织不致密，在较长时间内试样浅表水分扩散至表面足以赶上表面的汽化，因此各温度下均有较长的恒速段，这阶段的传质属表面汽化控制；随干燥的继续进行，试样表面的实际汽化面积逐渐减小并向试样内部迁移，此时所失水分大部分是物料的结合水分，而其平衡蒸汽压小于纯水，试样内部水分扩散速率较慢，因此出现了较长的干燥降速阶段，此阶段的传质属物料内部迁移控制；温度高，前期失水较快，后期就少了，所以降速段的干燥速率降得快。

2.2 模型评价

用文献报道的6种干燥模型（表1）来拟合各温度的试验数据，得到各自的模型，再计算出各模型的R2、r与S2值，具体数据详见表2。

表2表明，从R2值和r值看，对番薯来说，Logarithmic、Page和 Wang and Singh模型的R2值和r值均大于0.99，拟合度均较高；Logarithmic模型的S2最小，说明该模型预测值与试验值之间的差距最小，S2值小说明拟合度高，因此Logarithmic模型最适用于试验数据的拟合。由于各农产品的组织结构、成分等有区别，因此适用的薄层模型也会不一样，如韭菜干燥适用Logarithmic模型［6］，苹果切片干燥适用 Modified Page模型［7］，南瓜干燥适用 Newton模型［11］等。

表1 常用薄层干燥模型Table 1 Common drying models for thin layer

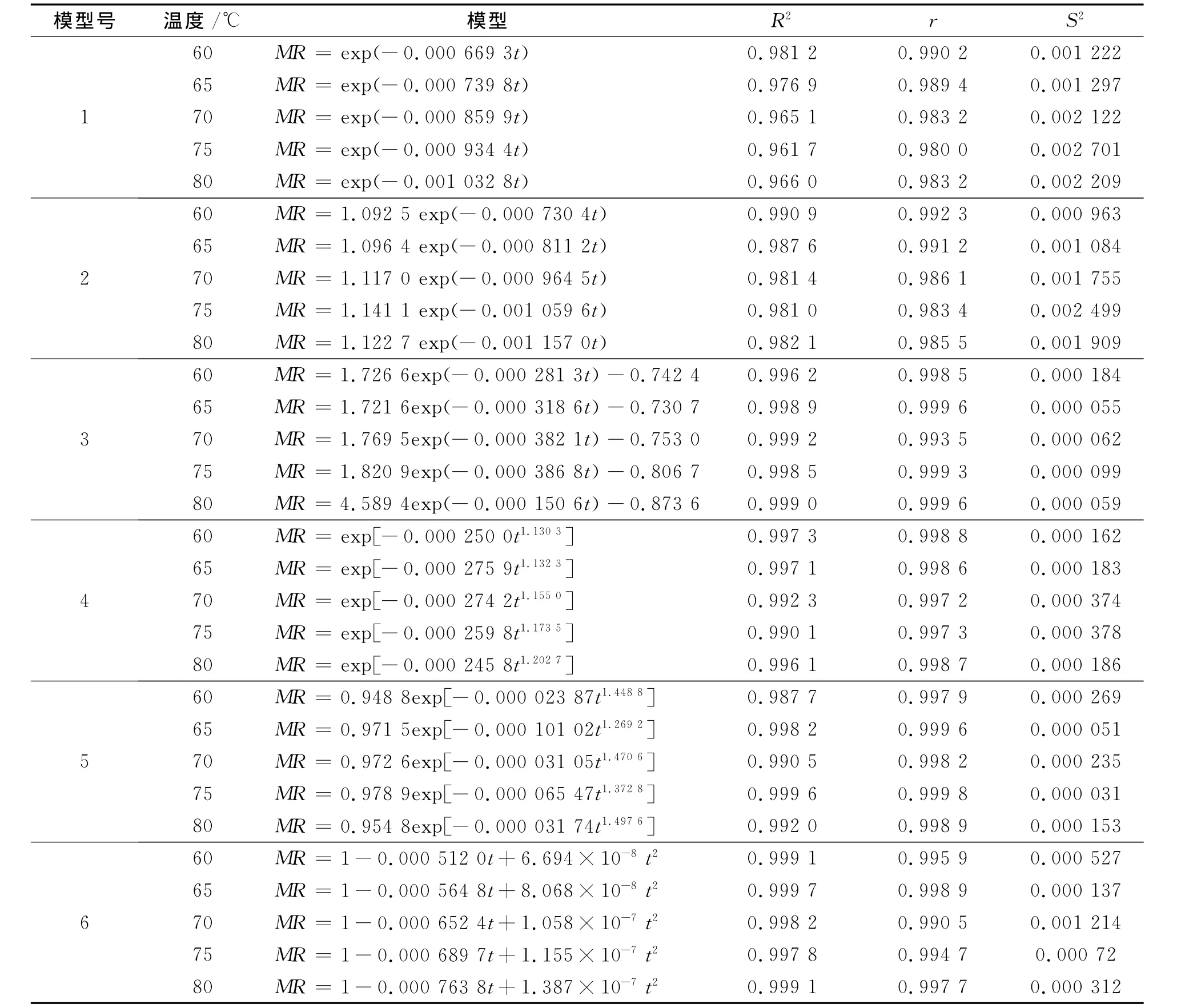
表2 不同干燥温度下拟合的模型和评价指标Table 2 Fitting models and evaluation indexes at different drying temperatures

2.3 不同温度下的有效扩散系数Deff与活化能Ea

研究了番薯片厚度2mm时各温度的Deff与干燥过程的Ea，计算得到各温度下的Deff见表3。

表3数据显示，有效扩散系数数值在文献［10］、［12］、［15］等所报道的范围之内；随热风温度升高，Deff增大，物料温度的升高，加剧了水分子的热运动，使水分子的扩散加快，这一结果与文献报道的一致。用式（10）关联表3中的数据，其关系见图3。

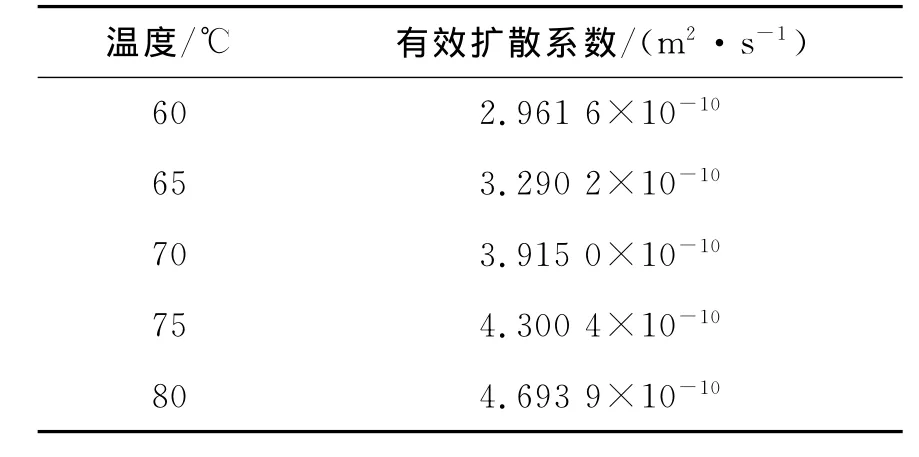
表3 不同温度下的有效扩散系数Table 3 Effective moisture diffusion coefficient at different temperatures

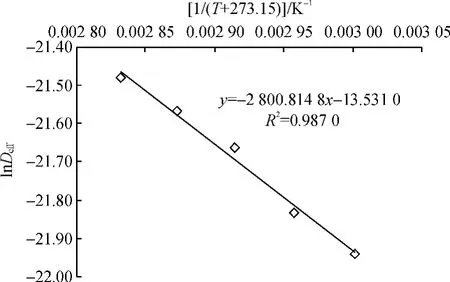
图3 lnDeff～1／（T＋273.15）关系Fig.3 Relationship of lnDeffand 1／（T＋273.15）

图3表明，lnDeff与1／（T＋273.15）具有良好的线性关系，说明符合阿累尼乌斯方程，则：D0＝e-13.5310＝1.329 1×10-6m2／s，Ea＝-8.314×（-2 800.814 8）＝23.29kJ／mol，数值较大，表明干燥温度对干燥过程有明显影响，与温度考察的结果相吻合。所得活化能值也在文献［10］、［15］所列果蔬活化能的范围之中。有效扩散系数与温度的关系式是

3 结 语

番薯片薄层热风对流干燥过程由较短的预热降速段、较长的恒速段和很长的降速段组成；热风温度越高，则干燥速率越大，水分比减小越快。比较模型评价指标，干燥试验数据最符合Logarithmic模型。风速0.946m／s、片厚2mm时，温度从60℃增高到80℃，水分有效扩散系数Deff从2.961 6×10-10m2／s增大到4.693 9×10-10m2／s，活化能Ea为23.29kJ／mol；所得热风温度对干燥的影响结果和Ea值均表明热风温度对干燥过程影响显著。

［1］ Aina A J，Falade K O，Akingbala J O，et al.Physicochemical properties of caribbean sweet potato（Ipomoea batatas（L）Lam）starches［J］.Food and Bioprocess Technology，2012，5（2）：576-583.

［2］ Hatamipour M S，Kazemi H H，Nooralivand A，et al.Drying characteristics of six varieties of sweet potatoes in different dryers［J］.Food and Bioproducts Processing，2007，85（3）：171-177.

［3］ Sahin A Z，Dincer I.Prediction of drying times for irregular shaped multi-dimensional moist solids［J］.Journal of Food Engineering，2005，71（1）：119-126.

［4］ Menges H O，Ertekin C.Mathematical modeling of thin layer drying of golden apples ［J］.Journal of Food Engineering，2006，77（1）：119-125.

［5］ Gornicki K，Kaleta A.Drying curve modelling of blanched carrot cubes under natural convection condition［J］.Journal of Food Engineering，2007，82（2）：160-170.

［6］ Doymaz I.Influence of blanching and slice thickness on drying characteristics of leek slices［J］.Chemical Engineering and Processing：Process Intensification，2008，47（1）：41-47.

［7］ 林喜娜，王相友.苹果切片红外辐射干燥模型建立与评价［J］.农业机械学报，2010，41（6）：128-132.

［8］ 肖红伟，张世湘，白竣文，等.杏子的气体射流冲击干燥特性［J］.农业工程学报，2010，26（7）：318-323.

［9］ 黄艳，黄建立，郑宝东.银耳微波真空干燥特性及动力学模型［J］.农业工程学报，2010，26（4）：362-367.

［10］ Lee J H，Kim H J.Vacuum drying kinetics of Asian white radish（Raphanus sativus L.）slices［J］.LWT-Food.Science and Technology，2009，42（1）：180-186.

［11］ Nawirska A，Figiel A，Kucharska A Z，et al.Drying kinetics and quality parameters of pumpkin slices dehydrated using different methods［J］.Journal of Food Engineering，2009，94（1）：12-20.

［12］ Chong C H，Law C L，Cloke M，et al.Drying kinetics and product quality of dried chempedak［J］.Journal of Food Engineering，2008，88（4）：522-527.

［13］ Diamante L M，Munro P A.Mathematical modelling of hot air drying of sweet potato slices［J］.International Journal of Food Science Technology，1991，26（1）：99-109.

［14］ Singh S，Raina C S，Bawa A S，et al.Effect of pretreatments on drying and rehydration kinetics and color of sweet potato slices［J］.Drying Technology，2006，24（11）：1487-1494.

［15］ Doymaz I.Thin-layer drying characteristics of sweet potato slices and mathematical modeling［J］.Heat and Mass Transfer，2011，47（3）：277-285.

［16］ 孟岳成，王君，房升，等.熟化红薯热风干燥特性及数学模型适用性［J］.农业工程学报，2011，27（7）：387-292.

［17］ 何少华，文竹青，娄涛.试验设计与数据处理［M］.长沙：国防科技大学出版社，2002：166-167.

［18］ Crank J.The mathematics of diffusion［M］.Oxford：Oxford University Press，1975.