钢琴的音源

张茂林，刘金寿

（1.国家轻工业乐器信息中心，北京 100122；2.大连大学，辽宁 大连 116622）

纵观各类乐器，能产生初始声波的音源主要有“弦、棒、簧、板、膜、管（空气柱）”6种，而钢琴的音源则是琴弦。按照“惠更斯原理”，所有发射子波的部件都可以看作波源，因而相对于听众，音板、琴体也可以看作是音源。所不同的是，琴弦是原始音源，音板、琴体乃是二级、三级音源而已。这里所说的音源一般常指“原始音源”。

一般弦乐器使用的琴弦较少，涉及的弦线规格也不多，而钢琴使用的琴弦数量既大、规格又广。1台现代钢琴大约采用了220根左右的琴弦，可谓数量之大；弦径涉及几十种，弦长区分约220种，可见规格之广。仅从钢丝弦径的角度来看，从钢琴最高音c5使用的细裸琴弦（直径0.725 mm，长约数厘米）到最低音A2使用的缠铜弦（芯线直径1.6 mm，长约1 m～2 m），就有近30种弦径规格；若考虑每根缠铜弦使用的铜线的直径，那么，钢琴用弦就要有60余种规格了；如果再计及弦的有效长度，则钢琴所用的约220根弦，弦长规格各有差异，这样算来，恐怕钢琴用弦就达到了约220种规格。

既然钢琴的原始音源是琴弦，那么，首先就有必要了解弦振动的物理原理。

1 理想弦与实际钢琴弦

基于日常经验，弦在振动发音时似乎将弦拉得越紧发音越高，而弦设置越长则发音越低。那么，到底什么叫做琴弦？其发音的高、低、强、弱取决于什么因素？

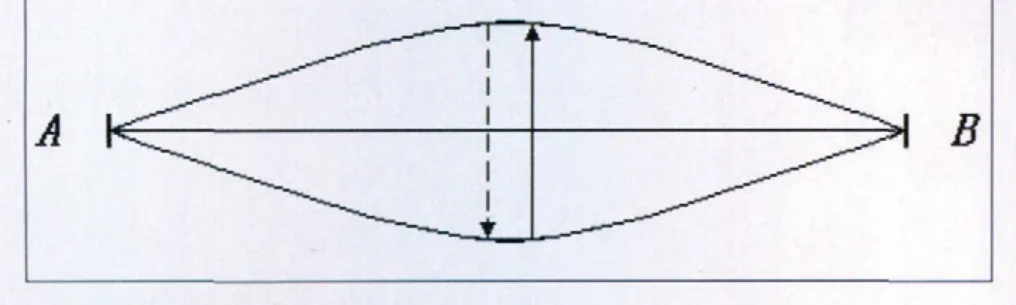
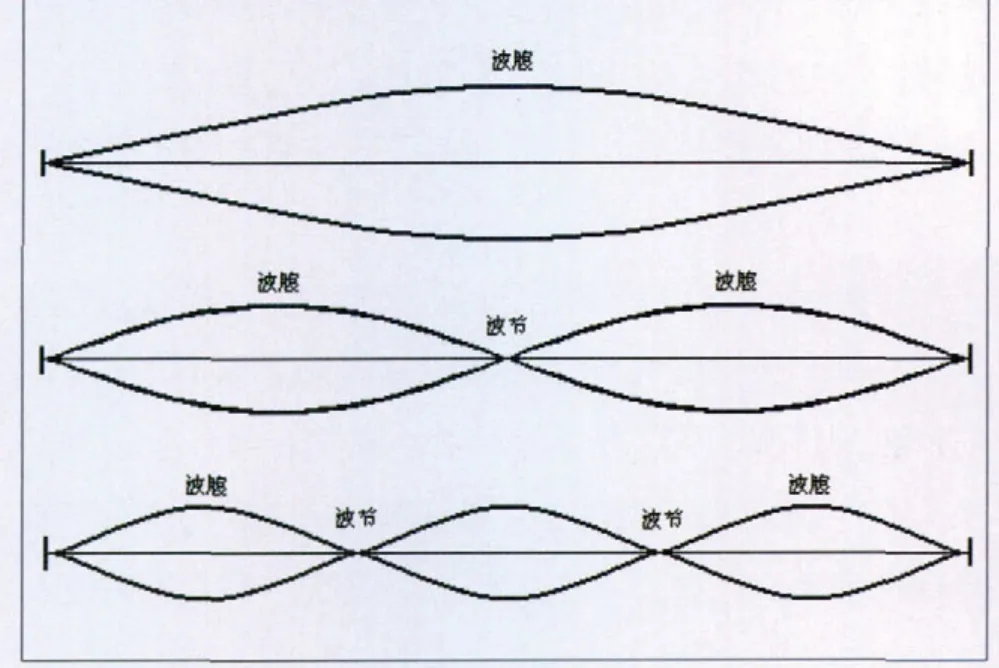
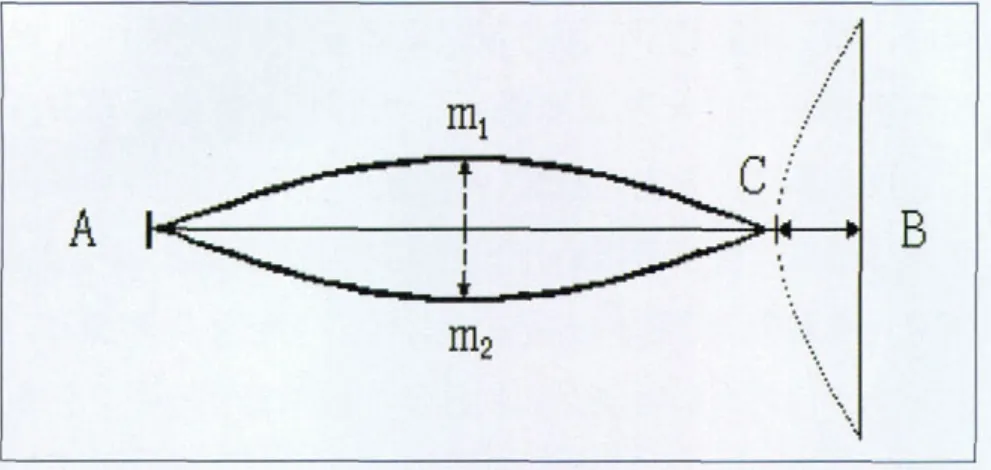
物理声学给琴弦下的定义是，张于2个固定点之间，由弹性固体材料构成的均匀、柔韧的细线称之为琴弦。但是应该知道，现实中绝对符合这个定义的琴弦根本不存在，它只能作为一种抽象的理想模型，因为，不能期望人工或大自然制成的弦能够达到完全的细瘦均匀，也不能追求绝对的柔韧和刚强。现实中，粗细、均匀、刚柔都是相对的。较刚硬的弦，一旦增加其长度，就会显得柔韧；而较粗的弦，如果是很长的一段，也会相对显得细。如此相对，反之亦然。这个道理实际就是数学分析中常用的“相对性原理”，例如，若有r<

上面虽然定义的是“理想弦”，但却可以为研究提供一个赖以比附的模型。在研究自然科学中常常是这样做的：定义一个现实中并不绝对存在的理想模型，却能够为许多研究的具体事物提供一个定量标准及一种理论规范。这样，就能够对许许多多的事物加以一定的条件限制，从而使其简化或近似为理想模型，以利于问题的研究和解决。例如几何学中的点、直线、平面，力学中的质点、光滑平面、匀速运动，电磁学中的点电荷、电偶极子、无限大带电平面、电流元、磁偶极子、无限长螺线管……按照这个思维，上述物理声学给琴弦下的定义实际上给了琴弦一个理想模型的定义。

图1 钢琴三音区的弦列概况

图2 弦振动的波腹波节与振幅

图3 琴弦的分段振动

在现实的众多弦鸣乐器中，绝大多数弦乐器的琴弦大体接近理想弦，都能够按照理想弦振动模型来做近似分析，因为它们大都比较接近柔、细、轻的理想模型，例如小提琴、吉他、二胡、柳琴等。可是，钢琴却有所不同，它的中音区琴弦比较接近理想模型，而高、低音区，特别是最高、最低两端琴弦却明显偏离了理想模型，原因就是高音弦太短，低音弦太粗（见图1）。因此，偏离理想模型较远的高、低两端音区，在实际调律中就出现了“高音偏高、低音偏低”的基频偏离十二平均律理论值的现象。这是一种必然，因为十二平均律的音高理论值是根据理想模型算出来的。

2 弦的振动方式

要使1根琴弦振动起来，必须具备4个条件。第一要有支点，第二必须悬空，第三要松紧适度（张力恰当），第四要施加激励（击奏或摩擦）。概括而言就是必须具备“端点、悬空、张力、激励”4个条件。具备了这4个条件而振动起来的弦，其振动方式与状态也较为复杂，一般用肉眼只能观察到它的横振动。实际上，当它受到激励时，还附加、包含有纵振动、扭转振动、倍频振动等等，只是因为它们较弱，难以被直接观测到。

2.1 横振动

横振动是一种与弦体走向相垂直的振动。弦的横振动粗看起来呈枣核形，其两端不动，为振动的“节”；中间振幅最大，为振动的“腹”，如图2所示。

值得注意的是，在弦的全长振动的同时，弦还做1/2、1/3、1/4……等分段振动，如图3所示。

全长振动产生基音，基音的频率基本决定着琴弦发音的音高；分段振动产生谐音（泛音），在理想情况下，它们是频率为基频整数倍的一系列谐音列（泛音列），谐音的多少及强弱则关系到弦音的音色与品质。

就理想弦而言，谐音的音量一般都要比基音的音量小。谐音的音波振幅（能量）大体与它们的序数成反比，是按1/n（n为谐音序数）逐级下降的，如第二谐音波的振幅为基音波振幅的1/2，第三谐音的振幅则为基音波振幅的1/3，第四谐音的振幅则为基音波振幅的1/4……

那么有没有泛音的振幅超过基音振幅的情况呢？笔者曾于1988年，在原北京乐器研究所反复观测过钢琴最低音的“第一泛音（即第二谐音）的振幅明显高于基音振幅，第二、三泛音的振幅明显偏强”的仪器显示情形，当时使用的是丹麦的电脑频谱分析仪。至于为什么会出现这种反常现象，笔者分析认为，主要原因当属钢琴最低音弦偏离理想弦模型较远，是最低音弦“过粗、过重、多层缠铜”既笨重又偏长的特殊结构，使其出现了第一泛音的振幅超越基音振幅以及第二、三泛音的振幅明显偏高的现象。这一“最低音弦的泛音振幅异常”的现象基本上揭示“为什么许多人分辨钢琴低音的音准困难”的原因。

图4 弦的纵振动

图5 弦的扭转振动

图6 竖琴琴弦的倍频振动

2.2 纵振动

弦做横振动时，其长度实际上也在做周期性变化，从而导致张力亦发生着周期性变化。这种张力的周期性变化会使弦同时产生纵向振动，即与弦的走向一致的伸缩运动，如图4所示。

在同一条弦上，纵振动的频率要比横振动的基频高得多，其本身也伴有一系列谐音，因而它们对弦发音的音色有一定的影响。各种乐器音色各异，有些乐器音色独特，其原因除了主要源于琴弦的泛音而外，与弦的该类纵振动也有关系。

纵振动的频率除与弦长、线密度有关外，还与弦材料的弹性模量有关。

2.3 扭转振动

当用琴弓擦弦或用手指、拨片拨弦时，弦除了做横振动、纵振动外，同时还会做扭转振动，如图5所示。

扭转振动的频率比横振动基频要低，其基音亦有一系列谐音伴随。扭转振动对弦发音的音色也有一定的影响。

扭转振动的频率除与弦长、密度有关外，还与弦的刚性系数有关。

2.4 倍频振动

由于弦乐器的挂弦点不是绝对固定的，所以，弦乐器一般都不同程度地存在倍频振动。弦在做横振动时，每完成一个周期，与弦连接的物体（如坚琴的音板）就会被带动并振动两次，其基频为横振动基频的两倍，故谓之倍频振动。如图6所示，C、B两点间距的长度即为竖琴音板发生倍频振动的幅度。

这种振动与弦的横振动同步，它加强了弦的二次谐波。倍频振动也有自身的谐音系列，它对弦发音的音色同样能产生一定的影响。

在乐器的实际演奏中，弦的上述4种振动方式常常是组合共存的。横振动必然引起纵振动，拨弦或擦弦又会引发扭转振动（击弦没有扭转振动），至于倍频振动，只要栓挂琴弦的部件在弦长的方向上有弹性，就总是会发生的。乐器的结构、激发弦的方法，决定了上述振动方式各自所占的份量和比例。

需要强调的是，在弦振动的所有方式中，横振动的能量最大，作用也最为突出和重要，其基频基本决定了发音的音高，其谐音列在弦的音色上起主导作用。正因为如此，不少文献、资料在论及弦振动时，只讲横振动而不提及其他3种振动方式。一般提及的“弦振动”，在没有特别声明时往往默指横振动。

3 理想弦的振动频率

在物理学中，称均匀、细长、轻质、柔顺弦为理想弦。理想弦振动的频率可按下面公式计算：

式中：

fn—频率； n—谐音序数（n＝1，2，3……）；—有效弦长；T—弦张力；—线密度。

由上式可知，振动频率与弦长成反比，与张力的平方根成正比，与弦的线密度的平方根成反比。利用上式不仅可以计算弦振动的基频，而且可以计算弦振动的各级谐频。

表1 理想弦各倍频数值表（取65.4075 Hz即C做基频）

……

这样，就得到了一根理想弦振动的一系列谐频表达：

f1，2 f1，3f1，4 f1，5 f1，6 f1，7 f1，8 f1，……

可见这一系列谐频都是 f1的纯倍频。倘若令 f1为小字一组 a1的基频，即f1= 440 Hz ，那么，就可得到该弦各级谐波的谐频：

440 Hz，880 Hz ，1320 Hz，1760 Hz ，2200 Hz，……

显然，改变弦长是用以改变频率的便捷途径，这一点已为许多弦乐器所利用。

上式既然是属于理想模型的，因此，用上式计算出的结果就与实际情况会有一些出入。因为乐器中实用的弦并非完全理想，它们有的相对柔、细、轻而近于理想，有的则相对偏刚、偏粗、偏重，偏离了理想弦的模型。还有，一些琴弦的振动也并非完全受张力制约，非张力振动产生的频率成分也不能用上式计算。但是，考虑到大部分琴弦比较接近理想模型，琴弦的主体振动又主要偏重于横振动，因此在讨论一般问题时，忽略次要成分，将振动频率分布按上式分析计算，基本不妨碍对问题主要矛盾的研究与解决。

表2 钢琴弦振动产生的14个分音及其与分音的和谐程度（取C1为基频）

图7 理想弦振动的谐音图 （以 C1音的前16个分音为例，不计及能量）

4 理想弦的谐音列

在弦的4种振动方式中，横振动的能量是最强的，它基本代表了弦振动的主要成分；用理想弦模型基本可以抽象地代表除了钢琴最高、最低音区以外所有琴弦以及其他各种乐器琴弦。因此，掌握理想弦横振动的谐音列，是理解钢琴弦以及其他乐器琴弦谐音列、音色的基础。

4.1 理想弦振动的谐音列是一个线性的纯倍频音列

设一条理想弦，其全长振动发出的基音为大字组的C音，则其分段振动所产生的一系列谐音（也称分音）的对应音高在五线谱中的相对位置如图7所示。

图7谱表中的每一个音都与下侧坐标标示的一个阿拉伯数字相对应，这些阿拉伯数字就是（1）式中的 ，它具有如下含义：

1）表示每个谐音的序数；

2）表示弦分几段振动；

3）表示各次谐音相对于基音（第一谐音）频率的倍数；

4）利用这些数字还可以计算各个谐音之间的频率比。

例如：

谱表中标以“l”的音（C）是第1谐音（也称基音），它对应于弦的全长即“一分段”的振动，其频率即为基频，是基频的1倍频，数值是65.4075 Hz；

谱表中标以“2”的音（c ）为第2谐音，它对应于弦的两分段振动，其频率是基频的2倍频，数值是130.815 Hz；

谱表中标以“3”的音（g）为第3谐音，它对应于弦的三分段振动，其频率是基频的3倍频，数值是196.2225 Hz；

谱表中标以“4”的音（c1）为第4谐音，它对应于弦的四分段振动，其频率是基频的4倍频，数值是261.63 Hz；

谱表中标以“8”的音（c2）为第8谐音，它则对应于弦的八分段振动，其频率是基频的8倍频，数值是523.26 Hz。

……

表1列出了理想弦各倍频数值，表2为钢琴弦振动产生的14个分音及其与分音的和谐程度。

4.2 谐音列各谐音之间的频率比

在理想弦的谐音列中，各谐音之间的频率比如下：

第2谐音与第1谐音（基音）的频率比为2∶1；

第3谐音与第2谐音的频率比为3∶2；

第4谐音与第3谐音的频率比为4∶3；

第5谐音与第4谐音的频率比为5∶4；

第5谐音与第3谐音的频率比为5∶3；

……

音乐工作者习惯把高于基音的谐音称为泛音，把谐音列称为泛音列。不管哪种称呼都应该注意，谐音的序数与泛音的序号并非相等，而是要错开一位。谐音的序号与泛音的序号具有如下的对应关系：

图8 钢琴的低音弦列

基音是一致的，但在谐音列中常称其为第一谐音；

第2谐音对应于第1泛音；

第3谐音对应于第2泛音；

第4谐音对应于第3泛音；

……

在学习与研究的过程中，分清谐音与泛音的对应序号十分重要，不可将二者混为一谈。

4.3 实际弦振动之谐音列的非纯倍频现象

在理想弦振动的谐音列中，各谐音的频率都是基频的纯倍数，即各谐音都是基音的倍频音。在数学中，将这样的纯倍频关系称作线性关系。与之相对应的是，实际的琴弦并非符合绝对的柔、细、轻，因而，它们或多或少地会具有偏离理想弦的倾向（见图8）。所以，在实际的弦振动中，各谐音的频率就不一定都是基频的纯倍频了，它们会相应地表现出对于纯倍频的一些偏离。但是在一定的精度范围内，为了讨论问题的方便，忽略这类影响不大的偏离，也不失为一种奏效的研究方法。通常将实际弦振动中谐音频率偏离纯倍频的现象，称为谐音列的非纯倍频现象，这种非纯倍频因素就构成了实际弦振动音波中的非谐成分，它也会影响音色的形成。

可以想象，在实际的弦振动中如果再计入其他3种振动方式的影响，上述的偏离纯倍频的现象可能还要加剧。实际琴弦谐音列的非纯倍频现象在一般的细弦乐器中并不明显，但在钢琴的高、低两端音区中却产生了不可忽视的影响。这种影响的直接效果就是，按照听觉调律即“充分保证八度纯”所校准的钢琴，出现了“高音偏高，低音偏低”的基频偏离十二平均律理论值的现象（见图9）。这个现象也是钢琴所特有的，因为只有钢琴两端音区的琴弦明显偏离了理想弦模型，并且它们发音的频率也比较接近人耳接受乐声的频段。

图9 钢琴的音准曲线

“高音偏高，低音偏低”现象的具体原因不止如此，详细的分析将在后面“听觉调律的基础训练”内容中讨论。需要说明的是，凡是不涉及钢琴的两端音区的讨论，套用理想弦振动的模型及其频率计算公式（1），一般不会太多地影响问题的实质。

4.4 弦振动谐音列中的非协和音

与十二平均律的具体音高相比，理想弦振动的第7、11、14谐音明显偏低，第13谐音明显偏高（见图7谱表）。这表明纯倍频的谐音与理想的十二平均律之间存在着不相容的成分，这种不相容恰恰说明了十二平均律与纯倍频音律——纯律的冲突。按照类似纯倍频谐音关系递推出的纯律，其各级音程与十二平均律的相应音程是不一致的。于是，上述明显偏低的第7、11、14谐音和明显偏高的第13谐音，还有与基音的音程关系为三个八度加大二度的第9谐音，以及因严重偏低而无法纳入乐音音阶的第13谐音，就构成了理想弦振动谐音列中的不协和成分。通常称这第7、9、11、13、14谐音为理想谐音列中的非协和音，正是这种非协和音的存在，引发了纯律的增四度、增五度、减七度、小二度等几个音程的合音具有最差的和谐程度，对应于十二平均律也如此。凡事物都有两重性，钢琴的这些非谐成分要比一般乐器的非谐成分能量大，可以设想它也更能影响到钢琴音色的个性。

5 击弦点

要让琴弦发音，必须要有激发它振动的着力点，该着力点可以被敲击、撞击、拨击，也可以被擦弦拉奏，笼统地称琴弦的该着力点为击弦点。钢琴弦的振动要靠木毡槌的撞击。乐器的设计、制作与演奏，很讲究击弦点的位置，这是因为该点位置与乐器发音的音色关系密切。通过调整或改变击弦点的位置，可以改变乐器发音的音色。

物理学家T·Young在研究用各种方法激发琴弦振动时发现：一条弦被激发振动时，波腹处在击弦点上时，其对应的分音被加强；而波节处在击弦点上时，其对应的分音则被抑制或消除。由此，他得出这样的结论：弹性体在一定位置上受激发使之振动，那么，这个位置是弹性体振动的波腹而不是波节；如果在一定位置上止住弹性体的振动，那么，这个位置是弹性体振动的波节而不是波腹。

例如：敲击琴弦的中部时，弦的中部必为振动的波腹而非波节，那么，波腹在此处的全弦振动（第一分音）、1/3弦长振动（第3分音）、1/5弦长振动（第5分音）……均被加强。而波节在此处的 1/2弦长振动（第2分音）、1/4弦长振动（第4分音）、1/6弦长振动（第6分音）……则被抑制或消除。

若激发弦的 1/4处，波腹处在此位的 1/2弦长的振动将被加强；而波节处于击弦点上相应的1/4、1/8、1/16等弦长的振动则被抑制或消除。

下面再介绍在一定位置上止住弦振动的情况。典型的例子是泛音奏法。在小提琴或二胡上，如果用左手指轻触弦长的 1/3处，用右手运弓擦弦，这时就能听到一个非常清纯的比基音高十二度（八度加五度）的泛音。这是因为，左手指轻触在弦的1/3处时，抑制、消除了波节不在此处的第1、第2、第4等等分音，只有第3分音的波节恰好处在止住弦振动的位置，而被保留下来。如果轻触 1/2、1/4位置，则可分别奏出高一个八度、高两个八度的泛音来。

T·Young的这个发现和结论被称为“杨氏定律”，该定律同样适用于弦以外的其他类型的乐声振动体。根据“杨氏定律”，通过调整乐器发音体的激发位置，可以在一定程度上改善乐器的谐音组合，从而改变了乐器的发音。这种激发位置的改变，有可能得到或是趋近于所希望得到和追求的音色。

乐器设计与制造家们历来都非常重视击弦点问题，对于钢琴而言更是如此。有学者用数学物理方程的计算表明，钢琴弦在正常条件的约束下产生的振动谐音列，一般都可以表述为正弦或余弦波的谐波序列。在琴槌的撞击下，琴弦的各次谐波一般都按照谐波序号n的倒数1/n的规律衰减；而拨弦情况下，琴弦的各次谐波则按照1/n2的规律衰减；擦弦情况下弓停则音消，几乎不存在余音，更谈不上衰减了。可见钢琴琴弦的泛音要比以其他激励琴弦的方式的乐器所产生的泛音要丰富、持久和强烈，这也是钢琴音色与众不同、个性独特、庄重美丽的原因之一。

当音槌中心恰好撞击在第n次谐波的节点上时，所对应的第n次谐波就受到制止不会出现。一条弦的第7、9、11、13、14分段的振动，能产生出与基音不相融合的一些非谐分音，所以若将弦槌击弦点选在弦长的1/7、1/9、1/11、1/13、1/14附近，可以有效地抑制这类与基音不相协和的成分，而使音质得到改善或美化。在上述7个非谐分音中，第7、第9能量最大，影响明显，所以在钢琴制造和调修中，常选琴弦的1/7、1/9处做击弦点，在最高音区可以考虑选弦长的1/13、1/14处做击弦点。

在钢琴的实际调修中，由于弦槌击弦的部位是一个有一定宽度的“曲面”而不是一个“点”，再加上寻找琴弦的1/7、1/9、1/11、1/13、1/14较难精确定位，所以，具体操作时就需要边试边调，操作经验和听觉功力就显得十分重要。调整钢琴弦槌击弦点的具体的方法就是，调制或修正弦槌与槌柄的仰角。在新装配钢琴时，通过调整槌柄和槌骨孔壁的胶结位置来进行，旧琴则需要用酒精烤棍加热融化槌柄和孔壁的粘胶，以微微改动琴槌的仰角来实现改变击弦点。笔者就曾经利用此法，通过调整高音区诸多弦槌击弦点位置的方法，提高了不少钢琴高音区的亮度，也消弱过一些钢琴高音的燥度。

[1] 缪天瑞.律学.北京：人民音乐出版社，1996

[2] 李时中.谈钢琴弦列最佳击弦点的理论与实践.乐器.1992（1）