一种高效的基音估计算法

高 悦，陈砚圃，闵 刚，杜 佳

（西安通信学院 基础部,陕西 西安 710106）

一种高效的基音估计算法

高 悦，陈砚圃，闵 刚，杜 佳

（西安通信学院 基础部,陕西 西安 710106）

分析已有的一些基音估计算法，对比其优缺点，提出一种可大大提高计算速度的高效基音估计算法。该算法是利用平均幅度差（MAMDF）法提取若干个可能峰值点，再利用计算精度较高的循环平均幅度差（CAMDF）法对这几个点进行验证，选取数值最小的点作为基音周期。由于只对几个点求CAMDF函数，因此运算量大大减小。

基音周期；基音估计；平均幅度差（AMDF）；改进的平均幅度差（MAMDF）；循环平均幅度差（CAMDF）

基音周期是语音压缩、合成以及识别中的重要参数，是语音信号处理中重要的一项，基音周期估计也因此成为大多数语音信号处理系统的重要组成部分。基音估计（Pitch Estimation）又称基音检测（Pitch Detection），它在有调语音辨意、低速率语音编码、说话人识别等方面具有关键作用，基音检测的最终目标是找出和声带振动频率完全一致的基音周期变化轨迹曲线，若不可能，则找出尽量相吻合的轨迹曲线[1]。基音周期估计一直是语音信号研究的重要课题，然而对此所提出的很多方法[2]都有其局限性。

由于语音信号是非平稳的时变信号，只有其中的浊音部分能够看作是准周期的，所以语音信号处理中通常采取短时处理技术。本文首先分析一些传统基音检测函数的特性，并比较其优缺点，在此基础上，提出一种新的基音估计算法，该算法不仅可减小倍频和半频的误判，而且能大大提高计算速度。

1 传统基音估计算法及其优缺点

1.1 自相关法（ACF）[3]

语音信号经加窗后的信号为Sn（n），Sn（n）的短时自相关函数为：

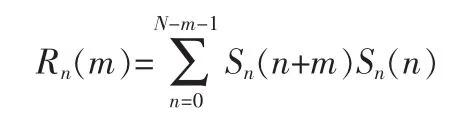
由于浊音是准周期信号，其最大值会周期性地出现，因此自相关函数实际上放大了其峰值。对于大多数浊音，语音信号的自相关函数都会有一些周期出现的局部最大值，第1个局部最大值与起点之间的距离即为基音周期[4]。清音的自相关函数则没有明显的峰值出现。因此通过检测是否有峰值就可判断是清音还是浊音。

自相关法是检测基音周期的有效方法，但因为求取自相关函数需要进行大量乘法运算，因此计算时间长，不适合实时应用。

1.2 平均幅度差法（AMDF）

平均幅度差函数AMDF（Average Magnitude Difference Function）的原理与ACF法相似，都是将周期性出现的点放大，所不同的是AMDF法求取的基音周期是第1个局部最小值与起点之间的距离。其定义为：

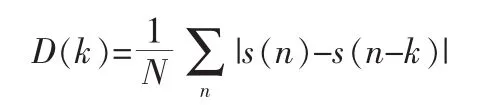
从D（k）的计算式看出，计算D（k）的差值项是不同的。随着k增加，求和的差值项数逐渐减少，结果导致D（k）的谷值幅度随着滞后时间k的增加而逐渐下降。因此，很难提取代表基音周期大小的谷值。有些方法设置多个阈值，以此筛选AMDF的谷值并进行有效性检验。然而，阈值的设置很难适用于所有语音，估计结果中选择倍频、半频，以及将清音误判为浊音的概率很高。

为了克服基本AMDF算法中谷值幅度随滞后时间增加而逐渐下降造成误判，在其基础上人们又提出许多新的算法，如变长的 AMDF（LVAMDF）、循环 AMDF（CAMDF）和改进的AMDF（MAMDF）等方法[5]。

1.3 改进的AMDF（MAMDF）

AMDF是一种用于估计基音周期的好方法，但由于其本身固有的缺陷，难以估计代表基音周期大小的谷值。由此，人们提出一种改进的AMDF方法，即以AMDF函数的最大峰值点（nmax,Rmax）与另一点（N,0）连接为一条直线，以这条直线与AMDF函数对应点之差作为线性变换的结果，由此得到修正的平均幅度差函数。这一变换的目的是对AMDF函数的各个周期谷值点的深度作线性缩减，同时将原函数的峰值和谷值点反转。在基音周期不是很大的情况下，以此方法进行变换后，将第1峰值与起点之间的距离作为基音周期，基本不会改变非平稳浊音语音的AMDF函数谷值特性和清音语音的AMDF函数特性，因此是比较准确的。但当基音周期较大时，由于这种线性缩减不能很好地修正AMDF函数,利用MAMDF方法仍会出现误判。

1.4 循环 AMDF（CAMDF）

基于以上算法的一些缺陷，一种新的CAMDF（Circular AMDF）函数[6]被提出,即采取类似于循环卷积的方法将AMDF函数重新定义为

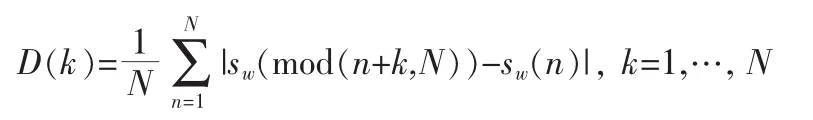
由CAMDF的定义可以看出，其原理与AMDF类似，在基音周期的整数倍点处会呈现显著的谷值点特征。但CAMDF函数与AMDF函数的不同之处在于,在计算幅度差函数D（k）时，当前加窗语音帧内的每个样本点都被使用且仅被使用一次，求和的差值项数也相同。因此，CAMDF函数值不会像AMDF函数那样因求和的差值项越来越少而呈下降趋势，其谷值点函数值会随着滞后时间k的增加而依次递增。这样，利用谷值点检测基音周期就更容易和有效。

由于CAMDF函数具有以上优点，它成为基音周期检测的有效方法。但由于每求取CAMDF函数的一个样点值，都要进行2N次运算，因此计算一帧的CAMDF函数运算量非常大，这样使其无法实时应用。这里在综合以上基音周期计算方法优缺点的基础上，提出一种综合多种方法优点的高效计算方法，既保留CAMDF函数计算精度高的优点,又避免CAMDF函数运算时间过长的缺点。

2 改进的基音周期检测算法

考虑到AMDF方法运算量较小，运算速度快，首先采用MAMDF法计算基音周期。理论上，求得MAMDF函数后，只要找到最大的峰值点即可得到所要求的周期。但由于语音信号的准周期性，有时最大峰值点所对应的点并不是基音周期，而真正的基音周期对应的点也可能并不是最大峰值点。因此，为了消除这种误判情况，在求出MAMDF函数的峰值点后，对峰值点所对应的MAMDF函数的函数值进行排序，取出最大的5个函数值，这5个函数值对应的点即为可能的周期点。

回顾已有的基音周期求取方法可发现，CAMDF方法是一种比较准确的方法，其误判率较低，基音周期的计算较准确。因此可采用准确率较高的CAMDF方法，仅对这5个点进行计算，然后对这5个点的CAMDF函数值进行排序，函数值最小的那个点与零点的距离即所要求的基音周期。采用这种方法，不但利用CAMDF函数可准确求取基音周期的优点，同时避免了该方法运算量大的缺点。

图1所示是对一帧语音求取MAMDF函数和CAMDF函数，MAMDF函数上的圆圈是对MAMDF函数取最大的5个峰值点：16，37，53，90，106。 CAMDF 函数上的圆圈是这 5 个点在CAMDF函数上的对应位置。可看出，第3个点的值最小，因此这帧语音的周期就是53个点。

图1 对一帧语音求取MAMDF函数和CAMDF函数

3 结束语

传统基于AMDF函数的基音检测算法中很容易出现基音估计加倍或减半的现象，CAMDF基音检测算法精度较高，但运算量太大。本文针对该现象，综合传统基音检测算法的优点，提出一种新的基音检测算法。由于该基音检测算法只需计算5个点的CAMDF函数，而传统CAMDF算法需对一帧中的所有点进行计算，因此大大减少运算量，简化基音检测过程。

[1]杨行俊，迟惠生.语音信号数字处理[M].北京：电子工业出版社，1995.

[2]冯 康，时慧琨.语音信号基音检测的现状及展望[J].微机发展，2004，14（3）：95-98.

[3]Rabiner L R.On the use of autocorrelation analysis for pitch detection[J].IEEE Trans.1977，ASSP-25（1）：24-33.

[4]鲍长春.低比特率语音编码基础[M].北京：北京工业大学出版社，2001.

[5]成新民，曾毓敏，赵 力.一种改进的AMDF求取语音基音的方法[J].微电子学与计算机，2005，22（11）:162-167.

[6]张文耀，许 刚，王裕国.循环AMDF及其语音基音周期估计算法[J].电子学报，2003， 31（6）：886-890.

An effective pitch estimation algorithm

GAO Yue， CHEN Yan-pu， MIN Gang， DU Jia
（Base Department,Xi’an Communication College,Xi’an710106,China）

This paper analyses and compares some existing pitch detection algorithms,then puts forward an effective pitch detection algorithm which improves calculation speed.This algorithm uses MAMDF method picking up some possible peak values.Then verifies their values with high-precision CAMDF,the point which has the minimum value is the pitch.The computation reduces greatly because only several points’CAMDF function are are computed.

pitch； pitch estimation； average magnitude difference function（AMDF）； MAMDF； CAMDF

TN912.3

A

1674－6236（2010）01-0024-02

2009-09-29 稿件编号：200909103

高 悦（1973—），女，陕西西安人，博士，讲师。研究方向：语音信号处理。