微型电动汽车用FSPM调速系统建模仿真

刘涛只，全 力，朱孝勇

(江苏大学，江苏镇江 212013)

0 引 言

当前，以内燃机为动力的传统汽车虽然在发展，但受到石油资源的减少和环境污染这两大难题的制约，具有无排放、噪声较低和效率较高等优势的电动汽车逐渐受到人们的重视。世界各大汽车公司以及各国都大量人力物力用于电动汽车的研究开发。

电动汽车体系中的一个重要分支是微型电动汽车。微型电动汽车，是指最高时速低于50 km，整车重量低于600 kg，一次充电续航里程为70～130 km一类纯电动汽车。由于微型电动汽车具有质量轻、价格低、体积小、低速性能好等优点，是一种特别适合中小型城市及广大农村运行的短途交通工具，出现之后便立即受到了国内外相关领域企业和学者的关注。

微型电动汽车是由储能电池和能量管理系统、车体、电机驱动系统组成的一类新型运载车辆。蓄电池及电池管理系统技术、车体技术、电机及其驱动控制系统技术等是微型电动汽车的关键技术。

与普通微型汽车相比，微型电动汽车减少了发动机动力系统，包括减速箱、起动电机、水冷却和油箱等部件，增加了电机、驱动控制系统和充电系统。考虑到微型电动汽车存在频繁起动、加速、巡航、减速、爬坡等工况，且一般仍采用电压等级为48 V/60 V/72 V的铅酸电池供电，因此低压大电流电机在微型电动汽车领域得到了广泛应用。

本文在理论分析基础上，以一台低压大电流磁通切换电机作为控制对象，应用MATLAB/Simulink构建了基于SVPWM的磁通切换电机驱动系统的仿真模型，并通过仿真及实验验证了系统具有稳态精度高、动态响应快、抗扰动能力强等优点，对所提出的SVPWM控制方法进行了有效性验证。

1 磁通切换电机的结构及工作原理

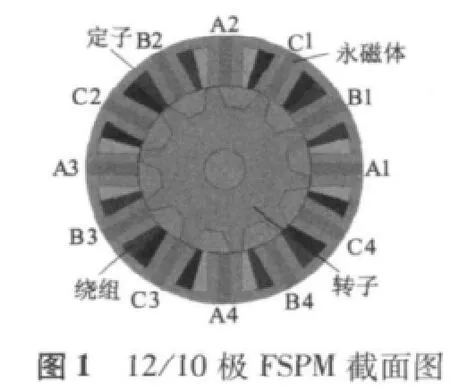
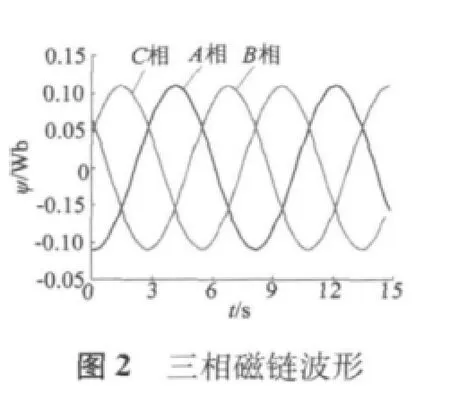
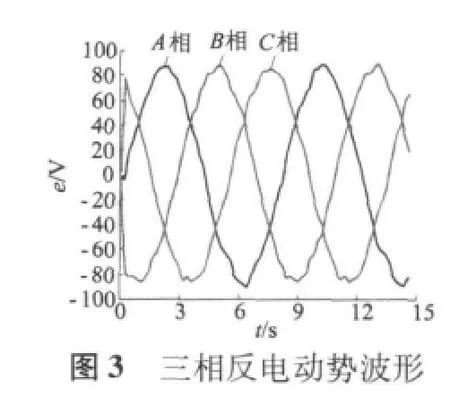
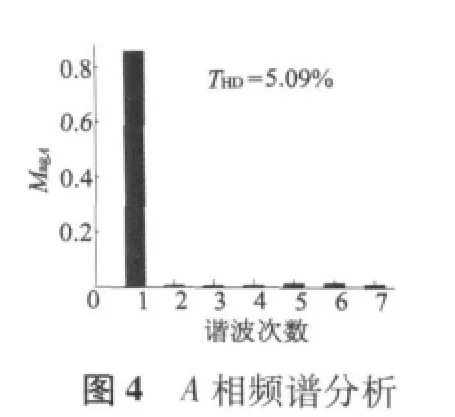
磁通切换电机(以下简称FSPM)是一种新型结构的定子永磁型电机，其结构完全不同于转子永磁型电机。图1为一台三相12/10极FSPM的截面图。电机的转子部分为凸极结构，上面既无绕组也无永磁体。定子也是凸极结构，采用集中绕组，绕组端部较小，节省用铜量并减小铜耗。定子中12个线圈共分成了三组，每四个串联组成一相，例如图中的A1～A4是A相的四个线圈，以此类推。每个线圈绕组横跨在两个定子齿上，中间嵌有一块交替充磁的永磁体。磁通切换电机FSPM绕组里匝链的磁通(磁链)会根据转子的不同位置切换正负极性和数值大小。在一个转子极距范围内，对应着电机的一个电周期，磁通的数量会从最大变到最小，方向从进入绕组到穿出绕组。磁通切换电机的特殊结构决定了其定子上每相绕组具有一致性和互补性，确保磁通切换电机每相的永磁磁链、反电动势和电枢电流的波形为正弦波。图2和图3分别为电机在额定转速750 r/min下的三相磁链波形和反电动势波形，图4为A相频谱分析结果。

2 FSPM的结构及工作原理

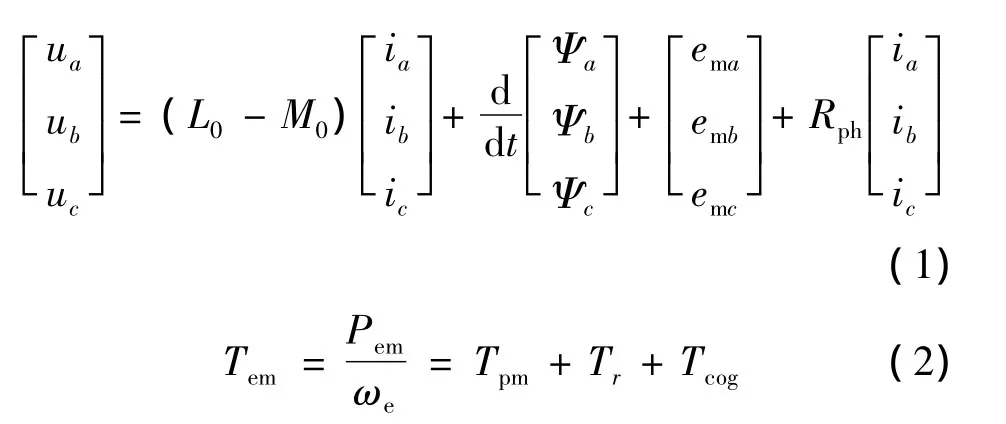
三相FSPM在定子坐标系下的数学模型:

式中:ua、ub、uc为三相相电压;L0为自感的基波直流分量;M0为互感的基波直流分量;ia、ib、ic为三相电流;Ψa、Ψb、Ψc为三相相绕组匝链的总磁链;ema、emb、emc为三相反电势;Rph为每相绕组电阻;Lm为自感波形的脉动幅值;pr为电机转子极数;θr为转子位置角;Tpm为电机永磁体产生的永磁磁链与电枢电流作用产生的永磁转矩;Tcog为电机定位力矩;Tr为电机磁阻转矩;Pem为电机电磁功率。

其中:

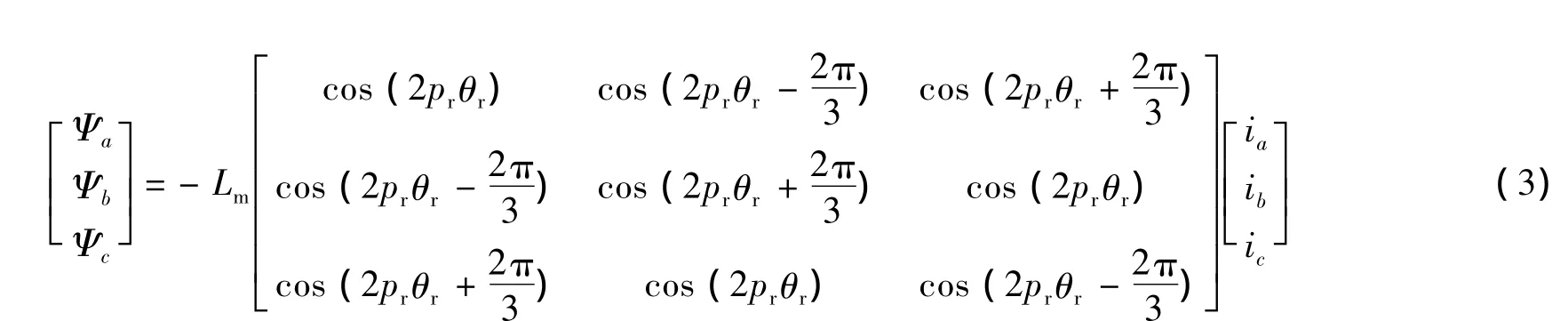
忽略电动机铁心饱和，不计电动机中的涡流和磁滞损耗，经过三相Park变换后FSPM在转子坐标系下的数学模型:

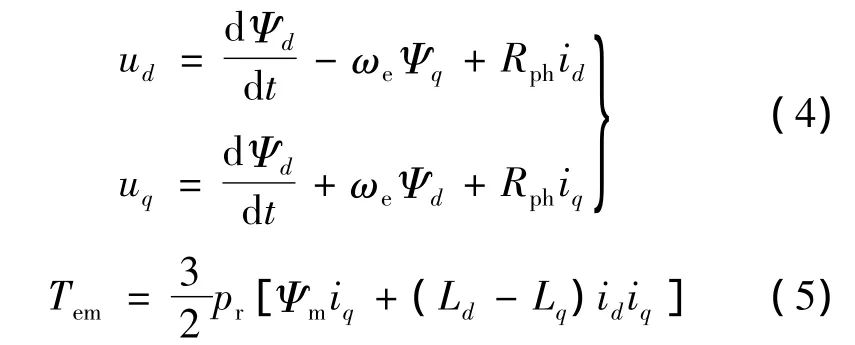
式中:ud为电机交轴电压;uq为电机交轴电压;Ψd、Ψq分别为电机d、q轴绕组中匝链的总磁链;ωe为电机转子的电角速度;Ψm为绕组中匝链的永磁磁链的峰值;Ld、Lq分别为直轴和交轴电感;id、iq分别为直轴和交轴电流。

3 FSPM调速系统的建模

基于FSPM的数学模型，本文对FSPM的SVPWM控制系统仿真建模，采用外速度环和内电流环的双闭环控制方式，如图5所示。

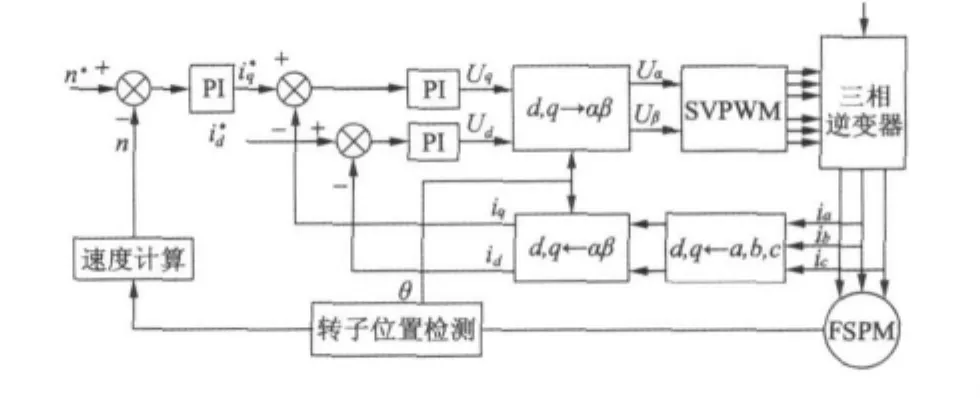
图5 FSPM调速系统原理图

本系统中，经过测量可得电机三相定子电流ia、ib、ic，经Clarke变换和Park变换为实际直交轴电流id和iq。参考交轴电流由实际转速与给定参考转速的差值通过控制器得到，直交轴电压Ud和Uq由实际交直轴电流id和iq分别和参考直交轴电流比较后经电流调节器生成，再经过变换模块得到控制电压Uα、Uβ，最后经过SVPWM模块生成六路脉冲信号来驱动逆变器模块产生三相电压，控制电机转动。

主要功能包括交通控制系统、运输系统、在物联网基础上建立起来的车辆状况监测和管理系统、对车辆进行控制系统、行车路线的管理和规划系统等，利用电子系统对这些功能进行集中协调和管理。

3.1 电机模型

系统建模的关键在于电机本体的建模。可以根据FSPM的数学模型中三相电压方程建立三相绕组子模块;根据三相输出转矩方程和机械运动方程建立运动子模块。最后将这些子模块通过接口模块组合起来就是电机子系统的模型，如图6所示。

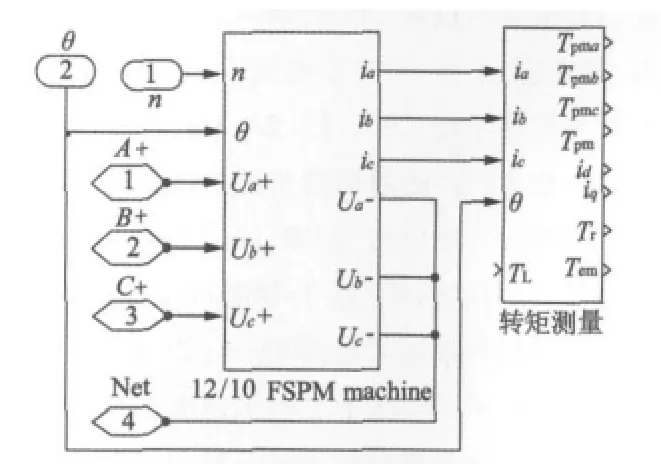
图6 三相FSPM电机仿真模型

图中“A+”、“B+”、“C+”为三相绕组与功率变换器主电路相连的三个端口;“Net”是与分裂电容中点相连的三相绕组的公共端;θ为转子位置的机械角度，它由给定转速与时间的乘积得到，单位为(°);n为给定转子转速，单位为r/min。

3.2 SVPWM 模型

利用MATLAB可建立如图7所示的SVPWM仿真模型。SVPWM仿真模型主要包括坐标变换模块、扇区判断模块、T1、T2计算模块、导通时刻计算模块以及PWM波生成模块。

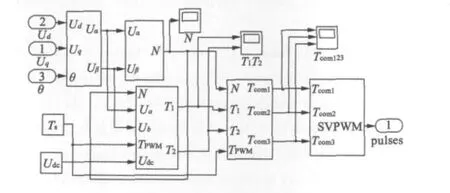
图7 SVPWM仿真模型

3.3 SVPWM控制系统仿真模型

SVPWM控制的FSPM调速系统的仿真模型如图8所示。

本文采用id=0控制方式。调速系统模型包括电机本体模型、SVPWM模型、三相逆变模型等。

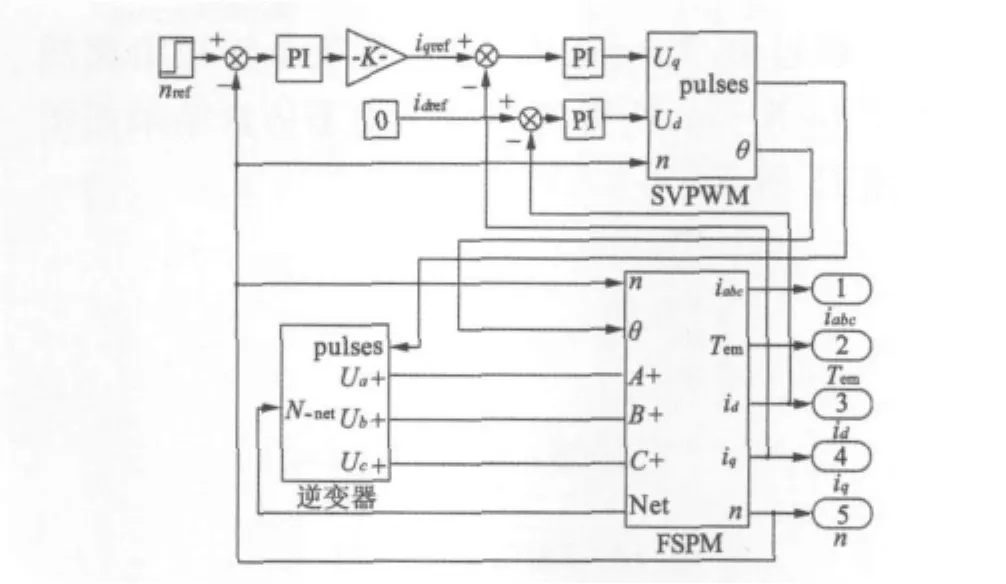
图8 SVPWM控制系统仿真模型

4 仿真分析

仿真所需的FSPM实验样机参数:定子齿数为12;转子极数为10;定子外径为160 mm;定子内径为100 mm;气隙长度为0.4 mm;转子内径为24 mm;有效轴长为80 mm;每相绕组匝数为30;额定转矩为25.4 N·m;额定电流为20.5 A;每相电阻为0.718 Ω;永磁磁链为 0.0987 Wb;摩擦系数为0.003 N·m·s，转动惯量为 0.008 kg·m2，功率器件的开关频率为10 kHz。

为了验证模型有效性，进行了以下的仿真实验:

(1)负载恒定，转速突变

保持三相FSPM的负载转矩18 N·m，当t=0.02 s时，将给定转速值500 r/min突然增加到700 r/min，所得到的电机动态仿真结果如图9～图12所示。

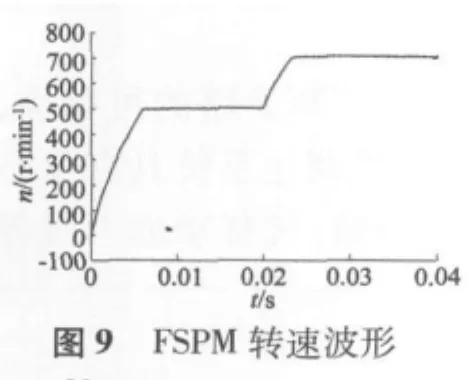
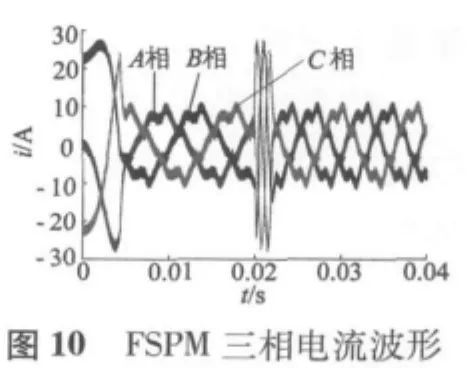
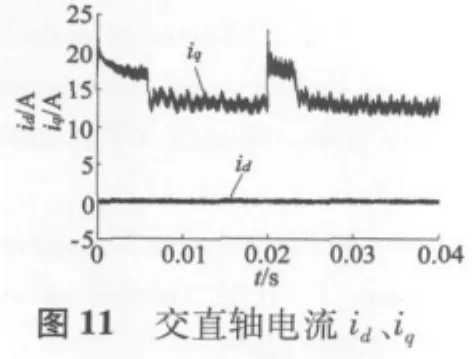
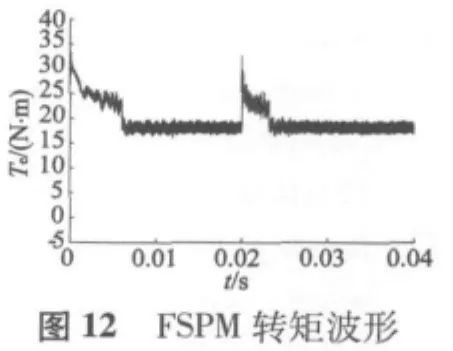
从仿真曲线可以看出，电机起动后，电机转速在0.005 s左右上升到给定值的转速值500 r/min，超调量很小，稳定后转矩波动较小。而当仿真时间到达0.02 s时，转速值由给定的500 r/min增加到要求的700 r/min，并且在0.025 s左右达到稳定，转矩也很快稳定且波动较小，可见系统满足电动车在行驶过程中加速工况的要求。

(2)转速恒定，负载突变

保持三相FSPM的转速500 r/min，电机从t=0开始空载起动，当t=0.02 s时，将负载转矩值突然增加到18 N·m，所得到的电机动态仿真结果如图13～图15所示。

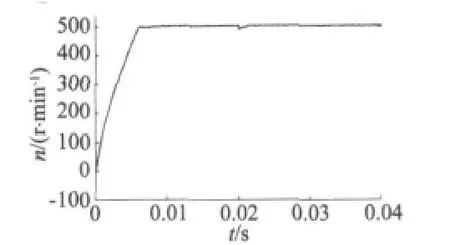
图13 FSPM转速波形

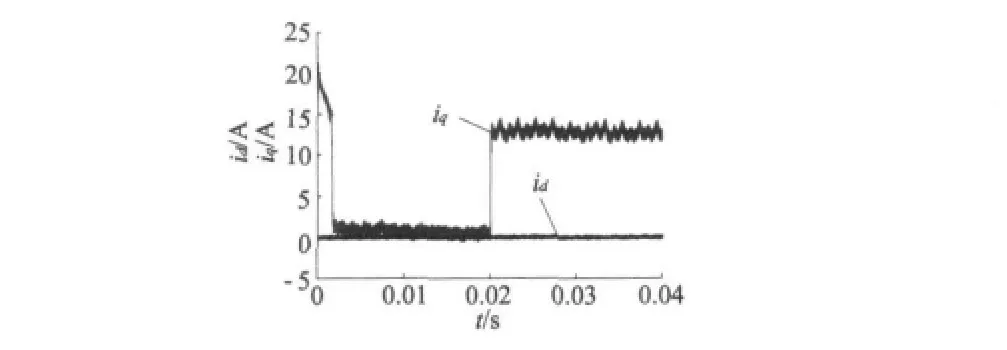
图14 交直轴电流id、iq

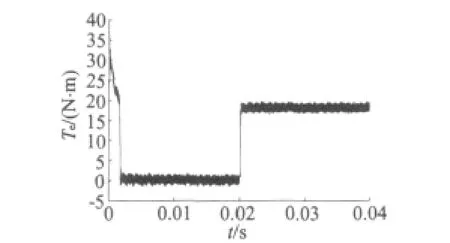
图15 FSPM电机转矩波形

由仿真波形可知，电机空载起动后，转速在t=0.005 s时稳定在给定值500 r/min，超调量小，稳定后转矩波动小，符合电动车起动工况的要求。t=0.02 s突加负载18 N·m时，电磁转矩立刻上升到给定转矩，电流也能立刻切换并稳定，符合电动汽车爬坡工况的要求。

仿真结果验证了SVPWM控制策略的可行性，以及SVPWM控制的FSPM电机调速系统具有稳态精度高、转矩脉动小、动态响应快、抗扰动能力强等优点。

5 结 语

本文主要在MATLAB/Simulink环境下研究了FSPM基于SVPWM的控制系统，并进行仿真。由仿真结果可知，系统的稳态精度较高，响应较快，电机定子电流及转矩在转矩负载突变后能较快趋于稳定，在转速突变后也能较快趋于稳定。仿真实验表明SVPWM控制系统对于FSPM调速系统控制的正确合理性，通过几个简单工况的仿真，进而验证了FSPM在微型电动车上的适用性。

［1］薛定宇，陈阳泉.基于MATLAB/Simulink的系统仿真技术与应用［M］.北京:清华大学出版社，2002.

［2］赵辉，鲁超，冯金钊，等.基于SVPWM的永磁同步电机控制策略研究［J］.电测与仪表，2009，46(7):14 －16.

［3］张春喜，廖文建，王佳子.异步电机SVPWM矢量控制仿真分析［J］.电机与控制学报，2008，12(2):160 －163，168.

［4］朱瑛，程明，花为，等.磁通切换永磁电机的空间矢量脉宽调制控制［J］.电机与控制学报，2010，14(3):45 －50.

［5］王妍，杜军红，陶伟宜，等.基于DSP的空间电压矢量法PWM的研究［J］.电机与控制学报，2000，4(2):98 －101，105.

［6］赵辉，鲁超，岳友军，等.基于三电平逆变器的永磁同步电机控制策略研究［J］.电气自动化，2010，32(3):1 －3.

［7］王艾萌，孙鹏纬，付超，等.基于SVPWM的永磁同步电机交流调速系统的实验研究［J］.华北电力大学学报，2005，32(2):15 －17.

［8］花为，程明，诸志强，等.新型磁通切换型双凸极永磁电机的静态特性研究［J］.中国电机工程学报，2006，26(13):129－134.

［9］陆炜，程明，花为.新型两相磁通切换型永磁电机调速系统建模与仿真研究［J］.微电机，2007，40(7):1－6.