半直驱风电系统最大功率跟踪和变桨距集成控制

刘广忱，王生铁，张 鸿，田桂珍

(内蒙古工业大学，内蒙古呼和浩特 010080)

0 引 言

并网风力发电是近十年来国际上发展速度最快的可再生能源技术之一，年均增长率超过25%，2010年底总装机容量达到 194.4 GW［1］。目前，主流风力发电系统(WPGS)可分为基于双馈感应发电机(DFIG)的齿轮驱动型WPGS和基于永磁同步发电机(PMSG)的直接驱动型WPGS两类。前者由于仍然有滑环和电刷，必须定期检修，后期维护工作量大，且不大适合在比较恶劣的环境下运行，一定程度上降低了系统的可靠性;而后者虽然减少了齿轮箱故障，降低了维护费用，但由于直接耦合，PMSG的转速很低，导致PMSG体积庞大，且造价较高。为了克服上述两种WPGS的缺点，芬兰的WinWinD公司提出了一种采用一级齿轮增速和多极中速PMSG的新型WPGS，即所谓的半直驱型WPGS(MWPGS)。该WPGS兼具直驱型WPGS的可靠性及传统多级高速齿轮增速系统的紧凑性，并可显著降低发电机成本、提高发电机效率［2－4］。

MWPGS的结构如图1所示，它包括两个背靠背的全功率PWM变换器，其控制系统主要包括:机侧变换器控制、网侧变换器控制、变桨距控制和偏航控制。其中，机侧变换器实现发电机侧有功、无功功率的解耦控制和最大功率跟踪控制［5－11］;网侧变换器实现输出有功、无功功率的解耦控制和实现低电压穿越［12－16］;变桨距控制限制输出功率，使机组安全稳定运行［17－20］;偏航控制实现风轮跟踪风向及自动解缆控制。

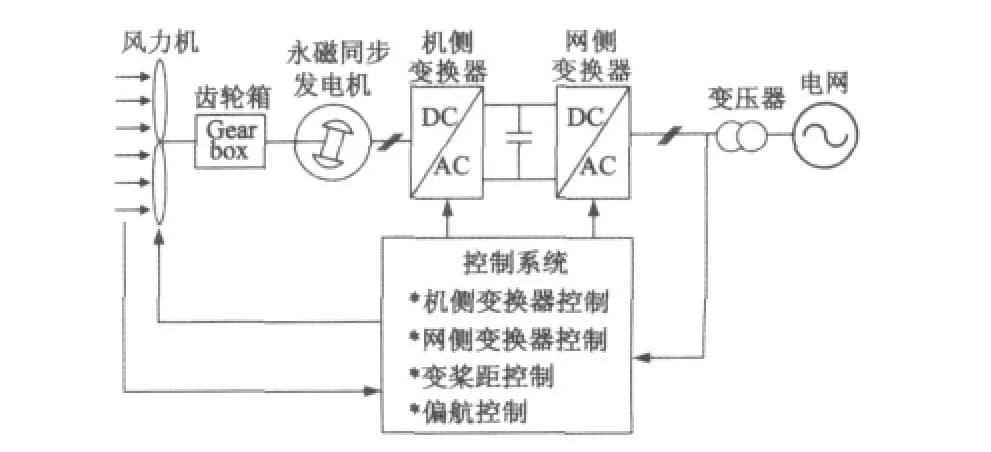
图1 半直驱风力发电系统结构图

本文主要研究最大功率跟踪和变桨距的集成控制策略，以期在随机风速和风力机工况频繁切换条件下，实现半直驱风力发电系统优化及可靠运行。

1 半直驱风电系统机侧部分数学模型

1.1 风力机模型

由流体力学可知，风力机从风中捕获的功率:

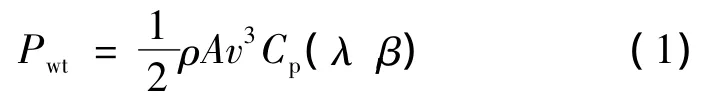
Cp(λ，β)是叶尖速比λ和桨距角β的非线性函数，可表示［13］:

由式(2)可得风力机风能利用系数特性曲线Cp(λ，β)，如图2 所示。

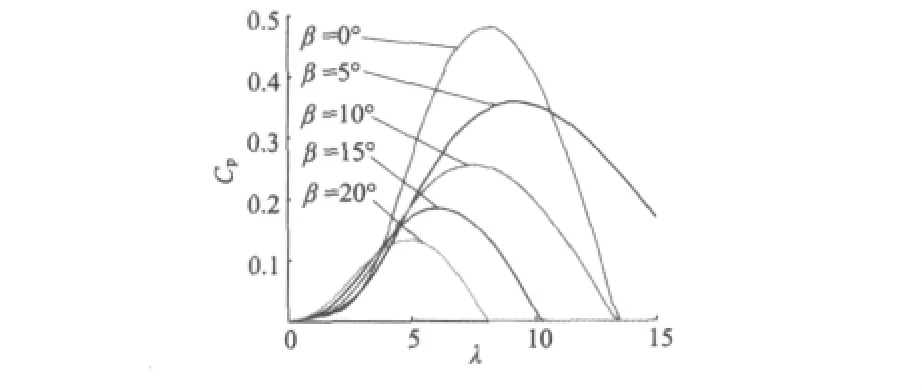
图2 风能利用系数曲线

由于变桨系统可以独立控制桨距角β，当风速大于切入风速而小于额定风速时，通常控制β=0°。从图2可以看出，此时存在且仅存在唯一叶尖速比λm对应于风能利用系数 Cp(λ，β)的最大值 Cpmax，即最佳叶尖速比。因此，当风速小于额定风速时，如果控制λ=λm，则Cp=Cpmax，即实现最大风能捕获。由图2中还可发现，Cp(λ，β)随 β的增大而减小。因此，当风速高于额定风速而小于切出风速时，可以通过增大β以降低Cp(λ，β)，减少风能捕获，从而控制输出功率恒定。

1.2 机械传动链模型

将增速齿轮箱和发电机转子的转动惯量折算到风轮转子侧，并假设传动系统的阻力全部集中于风轮主轴上，且主轴为刚性轴，则半直驱风力发电机组机械传动链的运动方程:

式中:Tm为折算到高速轴上的等效机械转矩;Te为发电机电磁转矩;J为折算到高速轴上的系统总转动惯量;F为系统总粘滞摩擦系数。

1.3 永磁同步发电机模型

在d－q同步旋转坐标系下，将d轴定向于转子磁场方向，q轴超前d轴90°，则永磁同步发电机的定子电压方程可表示［21］:

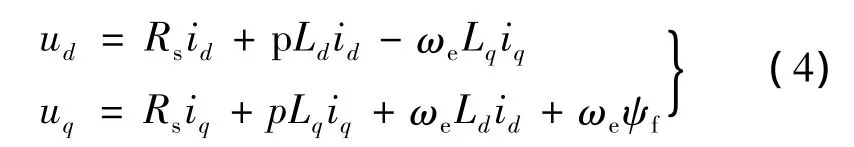
式中:ud、uq分别为定子电压的d轴和q轴分量;Ld、Lq分别为d轴和q轴等效电感;id、iq分别为定子电流的d轴和q轴分量;p为微分算子;Rs为每相定子绕组上的电阻;ωe为发电机的电角速度;ψf为转子永磁体磁链。

采用id=0的控制方式，发电机的电磁转矩可表示:

式中:Np为永磁体极对数。

1.4 变桨距执行机构模型

变桨距执行机构有电动和液压两种，目前多采用电动执行机构。为研究方便，将模型简化为一个一阶惯性环节，则变桨距执行机构传递函数［22］:

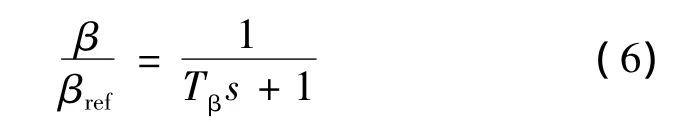
式中:Tβ为变桨距机构时间常数;βref为参考桨距角。

2 最大功率跟踪和变桨距集成控制策略

2.1 集成控制原理

风能具有随机性，风力机总是处于所有可能风速决定的不同工况，并进行较为频繁的切换。集成控制策略实现最大功率跟踪(MPPT)控制和变桨距控制的集成，在可用风速范围内(切入风速＜风速＜切出风速)，针对风况的不同，对半直驱风力发电系统采用不同的控制策略，以最大限度地获取风能及保证风电系统的可靠运行。集成控制结构如图3所示。

由图3可知，集成控制策略以转速控制为基础，以风速滞环判断为条件，针对不同工况，采取相应的控制策略。当风速小于额定值时，切入MPPT控制。此时转速环给定由最大功率控制模块提供，同时变桨距控制将β为零;当风速大于额定值时，进行变桨距控制。此时转速环给定为恒定量;当风速在额定风速附近波动时，滞环比较器可以防止风电机组在上述两种工作模态之间频繁切换。

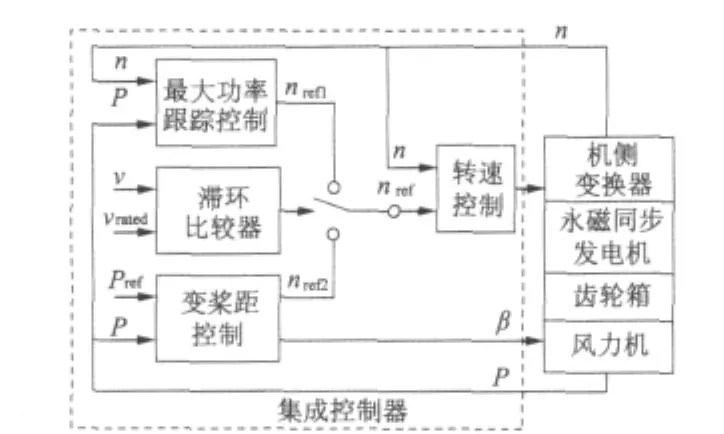
图3 最大功率跟踪和变桨距集成控制结构图

2.2 转速控制

发电机的转速控制结构如图4所示。由图中可知，系统采用转速外环、电流内环的双闭环控制结构，经过PI调节和电压前馈补偿得到参考电压指令。该指令通过利用电压空间矢量脉宽调制(SVPWM)技术控制变换器中各开关管的通、断，以调节发电机定子电流，进而调节发电机的电磁转矩，最终实现对风电机组转速的控制。

图4 发电机转速控制结构图

2.3 最大功率跟踪控制

常用的MPPT方法有叶尖速比法(TSR)、功率信号反馈法(PSF)和爬山法(HCS)三种。其中，TSR需要同时检测风速和发电机转速，并通过控制使叶尖速比维持最优值;PSF基于风机最大功率曲线进行控制，使得机组在不同发电机转速下的输出功率跟随指令值;HCS通过不断改变功率指令使机组输出功率逐步逼近最优值。由于HCS不需要了解最大功率曲线，对参数变化不敏感，也不依赖于风速的精确测量，实现方法简单方便，故本文采用该方法进行最大功率跟踪控制。

HCS又分为固定步长HCS和变步长HCS。前者采用固定转速扰动值进行爬山搜索，不能同时兼顾系统的快速性和稳定性，而后一种方法有效地解决了这一问题。因此，系统采取变步长HCS进行MPPT控制。变步长爬山法的最大功率跟踪流程如图5所示。

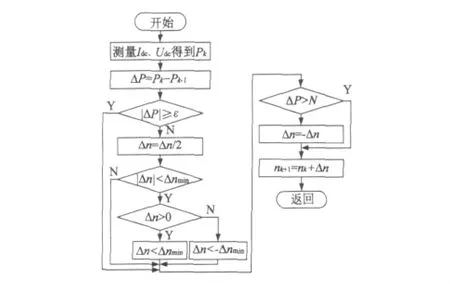
图5 变步长最大功率跟踪算法流程图

其最大功率跟踪原理为:风电机组在一给定转速下稳定运行一定时间后，给其一个转速扰动信号，计算当前输出功率P(k)，并与上一控制周期的输出功率P(k－1)比较得到ΔP，对ΔP进行判断。若ΔP＞0且数值较大时，Δn则保持其符号不变并采用较大步长;若ΔP较小，则通过二分法将Δn减半处理，并且为保证HCS的正确性，对Δn的最小值进行了限制。若ΔP＜0，Δn则取反，反方向进行HCS。该方法可同时兼顾系统的快速性和稳定性，当输出功率在山坡位置时，增大扰动步长，使转速迅速跟踪最佳转速，而当功率接近山顶时，减小扰动步长使转速平稳逼近最佳值。

2.4 变桨距控制

当风速大于额定风速时，受风电机组容量以及变换器容量的限制，系统将通过增大桨距角来降低Cp值，从而限制风力机捕获风能，以控制输出功率稳定在额定值附近并控制转速稳定在安全运行范围内。变桨距控制结构如图6所示。

图6 变桨距控制结构图

由图6可知，当风速高于额定风速时，将风机的输出功率P作为反馈量与参考功率Pref比较得到ΔP，该值通过桨距角调节器调节得到桨距角指令，然后通过桨距执行机构对风力机进行桨距调节，最终使得系统输出功率稳定在参考功率附近。

3 系统建模及仿真结果

3.1 系统模型及参数

基于上述分析，在MATLAB/Simulink环境下搭建了如图7所示的MWPGS机侧控制仿真模型。为便于对MPPT和变桨距集成控制策略的研究，将机侧变换器后的模型由带内阻的电压源与额定负载并联来等效。集成控制策略通过滞环比较器判断风速变化，实现MPPT和变桨距控制之间的可靠切换。其中，滞环比较器的上限值为9.5 m/s，下限值为额 定风速9 m/s。

图7 半直驱风电系统机侧控制仿真模型

以实验室现有实验系统为背景，半直驱风力发电系统参数如表1所示。

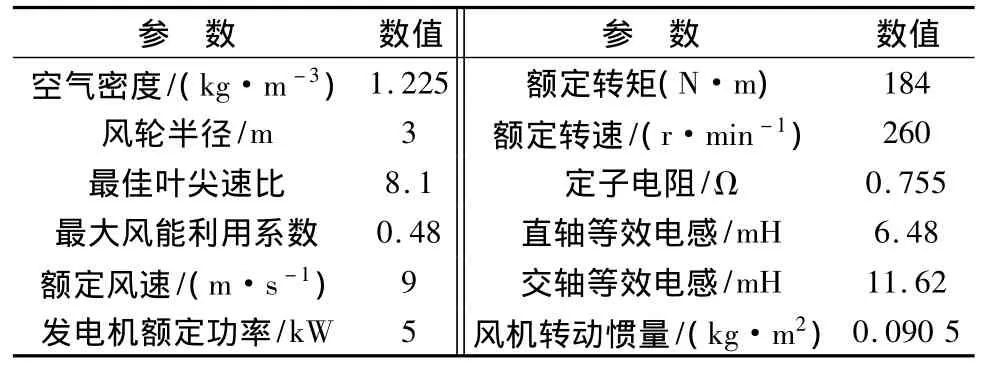
表1 系统参数

3.2 仿真结果及分析

3.2.1 渐变风响应

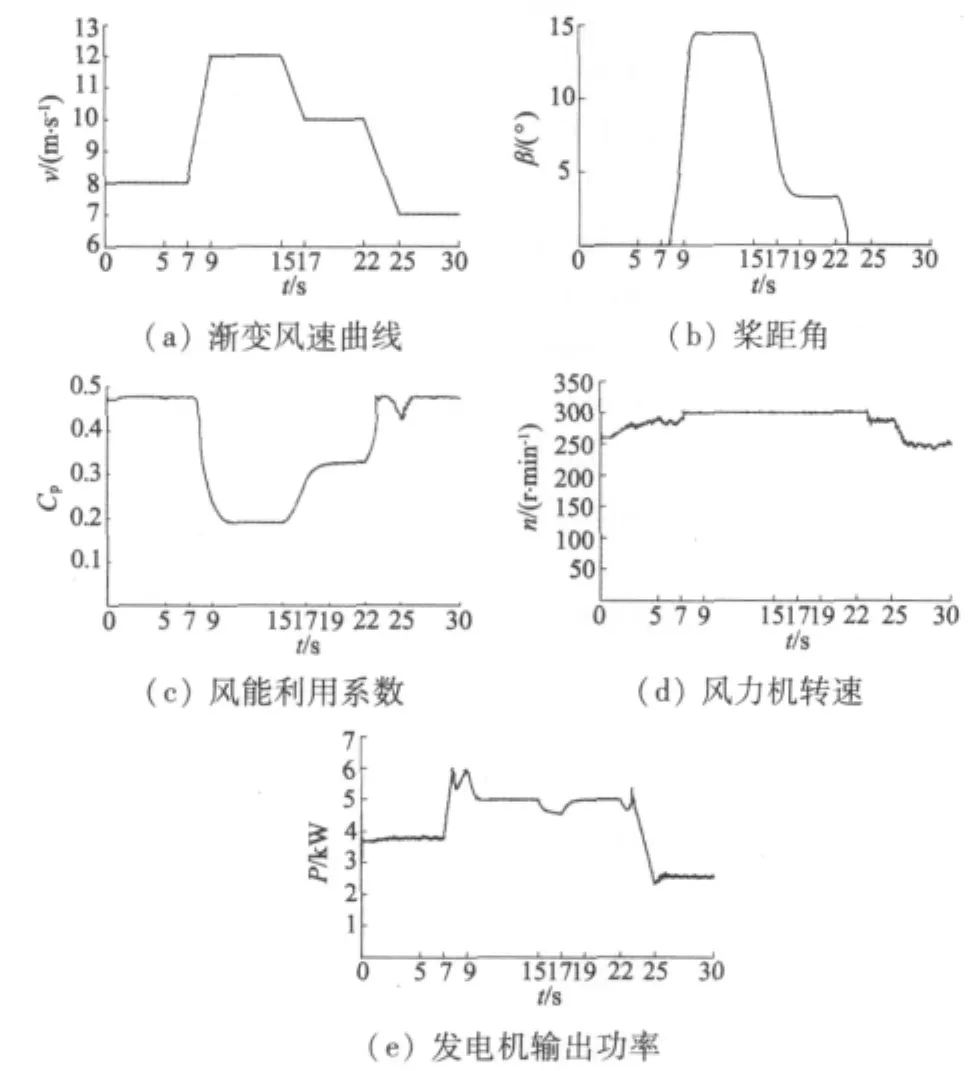
图8 渐变风速时风电机组集成控制响应曲线

在渐变风速条件下，半直驱风电系统集成控制响应曲线如图8所示。从图中可以看出，当初始风速为8 m/s时，系统进行MPPT控制，此时β=0°;7 s后，风速开始逐渐增大，当风速大于9.5 m/s时，系统切换到变桨距控制。v=12 m/s时，β=14.7°，Cp=0.18，转速稳定在300 r/min左右，功率控制在额定值5 kW附近;当风速由12 m/s渐变到10 m/s时，通过桨距角调节，最终使得系统输出功率稳定在额定值5 kW附近，转速稳定在300 r/min左右。此时，桨距角 β =3.25°，Cp=0.33;当风速由10 m/s渐变到7 m/s时，经历了变桨距控制到MPPT控制的切换，最终，β=0°，Cp值保持在最大值0.48左右，输出功率稳定在2.6 kW附近。

3.2.2 随机风响应

图9 随机风速时风电机组集成控制响应曲线

在随机风速条件下，半直驱风电系统集成控制响应曲线如图9所示。从图中可以看出，1～8 s，风速小于9.5 m/s，系统进行MPPT控制;8 s时，风速大于9.5 m/s，系统切换到变桨距控制。17～18 s，风速在9 m/s和9.5 m/s之间变化，由于滞环比较器的作用，系统仍进行变桨距控制;18 s，风速小于9 m/s，系统切换到 MPPT控制;18～22 s，风速在9.5 m/s以下，系统仍进行MPPT控制;22 s，风速大于9.5 m/s，系统切换到变桨距控制;22～24 s，系统进行变桨距控制;24～30 s，系统进行MPPT控制。总之，在随机风速作用的30 s时间内，集成控制策略在MPPT控制和变桨距控制之间进行了4次切换，获得了较为满意的控制效果。

4 结 语

风力发电是近十年来发展最为迅速的可再生能源发电技术。半直驱风力发电系统结合了当下两种主流机型DFIG和PMSG的长处，具有可靠性高和成本较低的优点。本文首先建立了半直驱风力发电系统机侧部分动态模型;其次，根据风能随机性及风力机工况切换频繁的特点，给出了半直驱风力发电系统最大功率跟踪和变桨距的集成控制策略。这种控制策略以转速控制为基础，以风速滞环判断为条件，实现不同控制模式之间的可靠切换，能够实现半直驱风力发电系统的优化及可靠运行;最后，在MATLAB/Simulink环境下进行了仿真研究，结果表明，在渐变风和随机风的作用下，集成控制策略能够实现最大功率跟踪控制和变桨距控制的可靠切换，获得了较为满意的控制效果，验证了本文所论控制策略的有效性。本文的工作将有利于半直驱风力发电系统的研究、开发与应用，对其它拓扑结构风电系统的控制也有参考价值。

［1］Global Wind Energy Council.Global wind capacity increases by 22%in 2010 － Asia leads growth［EB/OL］.2011－02－02:http://www.gwec.net/index.php?id=30＆no_cache=1＆tx_ttnews［tt_news］=279＆tx_ttnews［backPid］=4＆cHash=ada99bb3b6.

［2］WinWinD.WWD －3 Wind Turbine Datasheet［EB/OL］.www.winwind.fi，2008

［3］Polinder H，van der Pijl F F A，de Vilder G －J，et al.Comparison of direct－ drive and geared generator concepts for wind turbines［J］.IEEE Trans.on Energy Conversion，2006，21(3):725 －734.

［4］Grauers A.Efficiency of three wind energy generating systems［J］.IEEE Trans.on Energy Conversion，1996，11(3):650 – 657.

［5］Nobutoshi Mutoh，Atsushi Nagasawa.A maximum power point tracking control method suitable for compact wind power［C］//Power Electronics Specialists Conference.2006:1 －7.

［6］Wai R J，Lin C Y，Chang Y R.Novel maximum power extraction algorithm for PMSG wind generation system［J］.IET Electr.Power Appl.，2007，1(2):275 －283.

［7］Kelvin Tan，Syed Islam.Optimum control strategies in energy conversion of PMSG wind turbine system without mechanical sensors［J］.IEEE Trans.on Energy Conversion，2004，19(2):392 －399.

［8］房泽平，王生铁.小型风电系统变步长扰动MPPT控制仿真研究［J］.计算机仿真，2007，24(9):47 －50.

［9］Koutroulis E，Kalaitzakis K.Design of a maximum power tracking system for wind － energy conversion applications［J］.IEEE Trans.on Industrial Electronics，2006，53(2):486 －494.

［10］Liu Qihui，He Yikang，Zhao Rende.The maximal wind energy tracking control of a variable speed constant frequency wind power generation system［J］.Automation of Electric Power Systems，2003，27(20):63 －67.

［11］Datta R，Ranganathan V T.A method of tracking the peak power points for a variable speed wind energy conversion system［J］.IEEE Trans.on Energy Conversion，2003，18(1):163 －168.

［12］Liu G C，Wang S T，Guo J.Unified control for grid － side converter of multibrid wind power generation system［C］//2010 International Conference on Power System Technology.Hangzhou，China，2010:1－6.

［13］Conroy J F，Watson R.Low －voltage ride－through of a full converter wind turbine with permanent magnet generator［J］.IET Renewable Power Generation，2007，1(3):182 －189.

［14］Eloy － Garcia J，Arnaltes S，Rodriguez － Amenedo J L.Direct power control of voltage source inverters with unbalanced grid voltages［J］.IET Power Electronics，2008，1(3):395 －407

［15］Mohamed Y A － R I.Mitigation of dynamic，unbalanced，and harmonic voltage disturbances using grid－connected inverters with filter［J］.IEEE Transactions on Industrial Electronics，2011，58(9):3914 －3924.

［16］Sato A，Noguchi T.Voltage－ source PWM rectifier－ inverter based on direct power control and its operation characteristics［J］.IEEE Trans.on Power Electronics，2011，26(5):1559 －1567.

［17］夏长亮，宋战锋.变速恒频风力发电系统变桨距自抗扰控制［J］.中国电机工程学报，2007，27(14):91 －95.

［18］Senjyn T，Sakamoto R，Urasaki N.Output power leveling of wind turbine generator for all operating regions by pitch angle control［J］.IEEE Trans.on Energy Conversion，2006，21(2):467 －475.

［19］Boukhezzara B，Lupua L，Siguerdidjanea H，et al.Multivariable control strategy for variable speed，variable pitch wind turbines［J］.Renewable Energy，2007，1(32):1273 －1287.

［20］Baku M Nagai，Kazumasa Ameku，Jitendro Nath Roy.Performance of a 3 kW wind turbine generator with variable pitch control system［J］.Applied Energy，2009，9(86):1774 －1782.

［21］唐任远.现代永磁电机理论与设计［M］.北京:机械工业出版社，1997:244 －254.

［22］Horiuchi N，Kawahito T.Torque and power limitations of variable speed wind turbines using pitch control and generator power control［J］.IEEE Trans.on Power Systems，2001，1(7):15－19.