特种函数旋转变压器谐波补偿的有限元分析

张艳丽，杨为华，刘永平，邵焕清，桑 瑜

(中国电子科技集团第二十一研究所，上海 200233)

0 引 言

特种函数旋转变压器(以下简称特函旋变)误差补偿方法在文献［1］中已进行了详细的理论分析，本文采用二元有限元计算方法对一种55#机座的特殊函数的旋转变压器进行谐波补偿仿真分析，并通过试验数据进行分析验证。

1 特函旋变的原理

特函旋变由定、转子两部分构成，定子激磁，通过电磁感应，转子方输出一相与定子机械转角成特殊函数关系变化的信号，结构图如图1所示，原理图如图2所示。输出电压表达式:

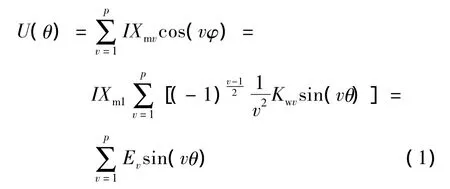
2 有限元分析模型

特函旋变输出电压U(θ)取胜转子转角θ的变化可以复现用户要求的函数关系，本文有限元仿真分析的特函旋变的曲线如图3所示。

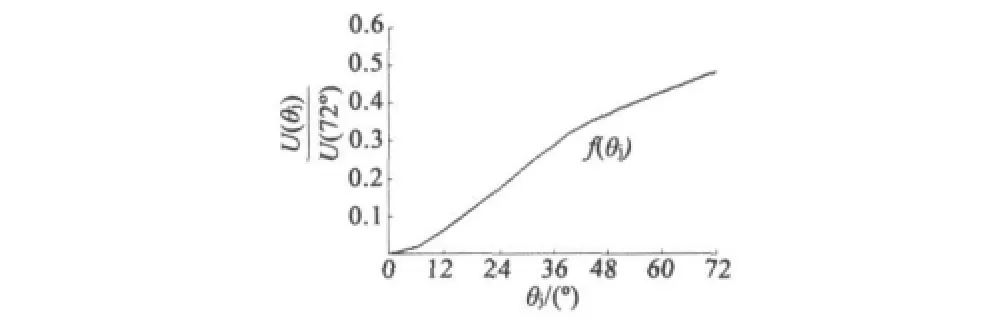
图3 特函旋变曲线

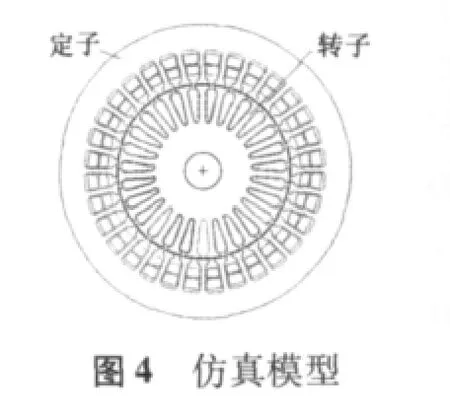
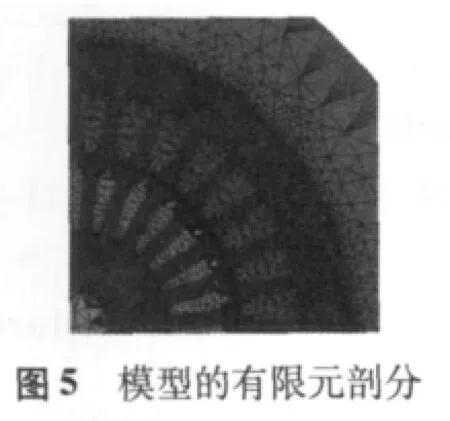
特种函数f(θj)旋转变压器二维暂态磁场有限元仿真模型的基本参数如表1所示，假定该旋转变压器工作理想状态，加在定子方激磁绕组上的电压E1=30 V，激磁频率f=400 Hz。为了分析谐波补偿对旋转变压器精度的影响，建立两个仿真模型，除定子绕组的匝数不同外，其余各种参数定义相同。定、转子均采用同心式绕组，模型1的定子绕组未进行谐波补偿，模型2中定子绕组是通过文献［2］中误差补偿计算方法进行了三次谐波补偿，图4为特函旋变仿真模型。为使剖分单元合理，采用静态场剖分，暂态场计算，图5为模型的有限元剖分图，有140000多个剖分单元。定、转子铁心材料为软磁合金带 1JH3，厚0.35 mm，气隙0.3 mm。

表1 仿真模型参数

3 有限元计算结果及分析

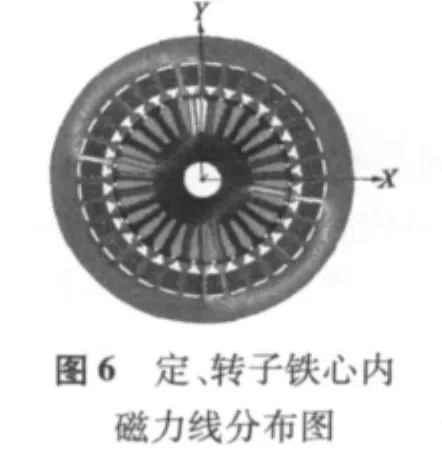
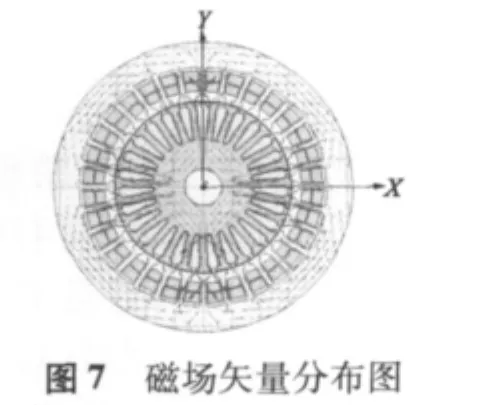
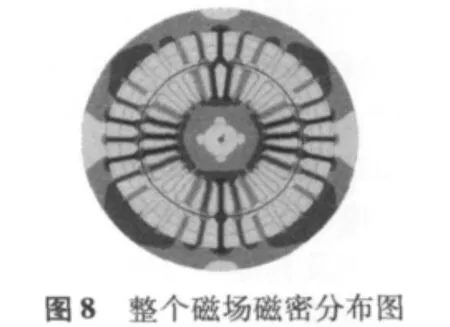
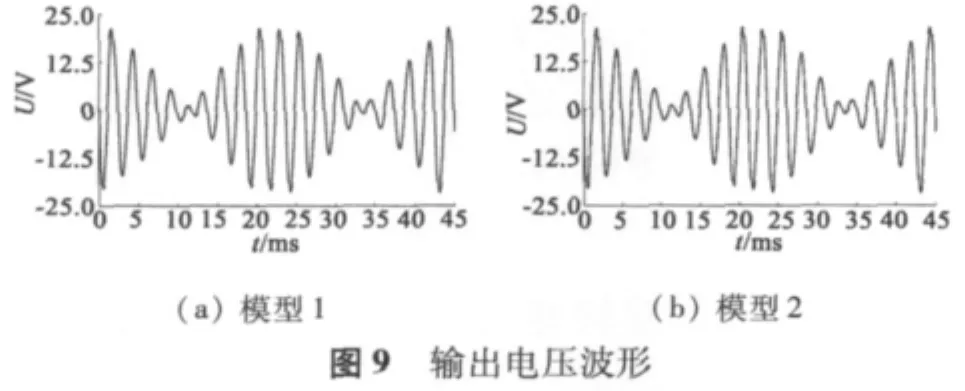
特函旋变二维暂态磁场有限元仿真结果如图6～图8所示。由图可知，该旋变的齿部磁密最大，设计时主要考虑齿部的磁饱和。特函旋变模型在一个电周期内的输出电压波形如图9所示。该特种函数f(θ)的使用范围是 0°～ 72°，每 6°测一点。

三次谐波补偿前有限元仿真计算误差值Δfm如图10(a)所示，最大误差点为30°位置，误差值约为－6.8‰，且误差值偏负值。

三次谐波补偿后有限元仿真计算误差值Δf'm如图10(b)所示，最大误差点为6°位置，误差值约为+3.9‰，通过谐波补偿，误差值明显降低，且误差值均匀分布在横轴线两侧。

图10 有限元计算误差值

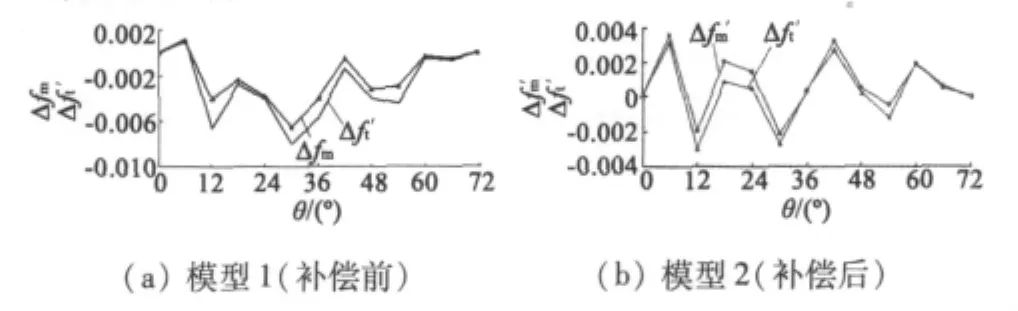
图11 计算值与实测值对比图

三次谐波补偿前后实测误差对比曲线如图12所示。本文试验数据曲线均为平均值，具体试验数据如表2所示。未进行谐波补偿前零级品为0，补偿后零级品为96%，产品精度显著提高。

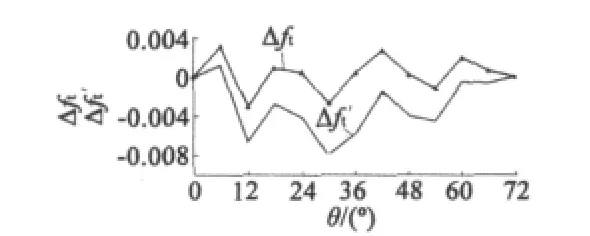
图12 三次谐波补偿前后实测误差对比曲线

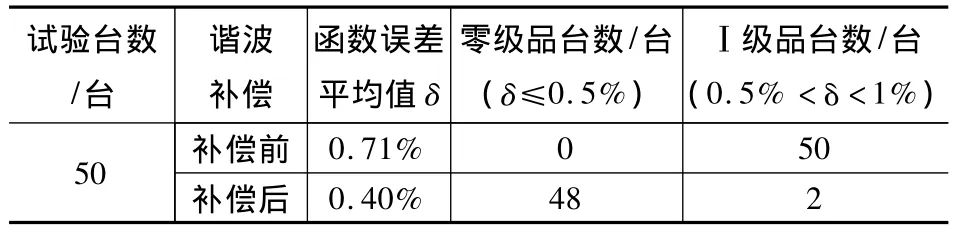
表2 特函旋试验数据

4 结 语

通过特函旋变二维暂态磁场有限元仿真结果和实验数据分析表明，采用有限元仿真分析有效验证了谐波补偿对降低误差的正确性及有效性，有限元磁场仿真有助于旋转变压器的设计及优化。二维磁场仿真忽略了定、转子铁心的端部效应，对转子斜槽也无法计算。为提高计算的精确度，考虑转子的斜槽情况，应进一步研究旋转变压器的三维磁场仿真技术。

［1］田恒安，陈燕玉，廖超宏，等.特种函数旋转变压器设计计算［J］.微特电机，1976(1):39 －64.

［2］张艳丽.特种函数旋转变压器的谐波补偿［J］.微特电机，2008(12):31－33.

［3］Lang C W.Special synchros for function generation［J］.Control Engineering，1968，15(12):75 －78.