FIR滤波在嵌入式系统中的实现与优化

杨秀朋

（贵州航天控制技术有限公司，贵阳 550009）

FIR滤波在嵌入式系统中的实现与优化

杨秀朋

（贵州航天控制技术有限公司，贵阳 550009）

介绍FIR滤波器的基本原理以及满足线性相位的条件，阐述了FIR滤波器的生成。从MATLAB得到的滤波器实现了在嵌入式中的移植，并进行了计算优化。通过对含有噪声的数据处理结果表明，该方法在工程实践中能满足要求。

FIR滤波器；MATLAB；嵌入式系统；算法优化

在嵌入式系统的采集控制应用系统中，采集到的原始信号往往是伴随着一些不希望出现的噪声。对噪声的处理可以采用硬件滤波或软件滤波。数字滤波器由于其精度高、稳定性好、使用灵活等优点，随着处理速度快、价格低廉的处理器的大量出现，使得数字信号处理技术在众多领域得到广泛应用。

数字滤波器根据冲击响应函数的时域特征，可分为FIR（有限长冲击响应滤波器）和IIR（无限长冲击响应滤波器）。FIR滤波器与IIR滤波器相比，具有严格的线性相位，幅度特性可任意等优点。应用FIR数字滤波可以实现相位的完全同步，这对于在相位严格要求的数据处理中有着重要意义。

MATLAB是一款功能很强大的工具软件，可以利用MATLAB软件中的工具箱完成运算量大的频谱分析以及滤波器生成等计算，从而克服嵌入式系统运行速度限制。根据信号与系统原理，滤波在时域就是输入信号与系统函数的卷积。因此在有了系统函数的基础上，就容易在嵌入式系统中实现FIR滤波。

1 有限冲击响应FIR具有线性相移的条件

FIR数字滤波器设计是采用多项式:

来逼近所要求的频率特性指标。由于它的单位冲击响应是有限长的,所以FIR数字滤波器是稳定的。由式（1）可以得到FIR数字滤波器的频率响应：

若要FIR数字滤波器具有严格线性相位，其相位和频率成线性关系，即相频特性满足：

虽然有初始相位θ0的存在，但它是一个群延迟并且是一个常数，对于滤波输出数据弥补相应的θ0完全可以实现滤波前后的同步。FIR数字滤波器具有线性相位的充要条件［3］是：

在式（4）中，N为滤波器的阶数，τ为滤波后的整体的延迟。在设计FIR滤波器时N（滤波器阶数）是已知的，因此整体导致的相移便是已知的，然后相应地平移τ个点，便可以实现相位同步。

2 滤波器的参数生成

FIR滤波器的设计任务，就是要决定一个系统函数H(z)，使它的频率响应满足幅度以及相位要求。由于嵌入式系统应用范围相对专一，信号的特征可以预知，加之速度受到限制，因此可以借助一些上位机软件（如MATLAB）来完成信号的频域分析。在信号频域分析的基础上根据应用需要确定相应的滤波指标，最后完成滤波器生成。对于采样频率处于几个固定值集合的情况，可以根据采样频率生成几个滤波器，根据不同的采样频率分别调用，从而完成滤波运算。

系统函数H(z)在时域对应h(n)，h(n)是一个长度为N的数组，将长度为M的输入信号input(n)与h(n)进行卷积运算，就可以得到滤波后的输出。

2.1 信号频谱分析

对于某系统采集的数据input［n］进行频谱分析，采样频率为2 000Hz，如图1所示。

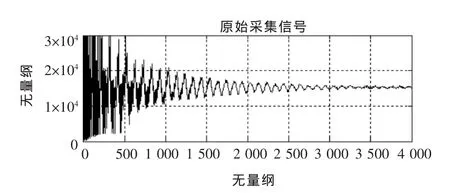
图1 原始输入信号

对上述信号频谱分析的m语言调用函数以及注释为：

若上述信号采样频谱为2 000Hz，在MATLAB命令窗口中执行 SpectrumAnalysis（input,2000）,便可以得到原始信号的幅度谱如图2所示。

图2 输入信号的频谱图

2.2 滤波参数确定

从图2可以看出有用信号的频率分布在50Hz以内，故确定滤波器的指标参数分别为：

（1）低通滤波，通带为50Hz，阻带为100Hz、阻带衰减80dB；

（2）为了确保相位严格可控，采用FIR滤波；

（3）为了确保所需频率成分无衰减通过，用Kaiser窗来实现。

在MATLAB命令窗口中输入fdatool命令，可以得到滤波器分析与生成界面。在该界面下生成的系统函数的幅频特性如图3所示。

图3 满足要求的FIR低通滤波器的频谱

从图3可以看出，该滤波器在通带范围内的衰减为0dB，这可以保证有用信号完全通过，高频杂波的衰减不少于80dB，足以保证滤波需求。

2.3 滤波器h(n)的生成

在 MATLAB中利用 fdatool工具箱［3］按要求生成相关参数h(n)，对于图3设计的滤波器通过“导入至工作空间”的方法，在工作空间中将保留为一个名称为h的归一化一维数组，如图4所示。该数组可以通过文本文档保留下来，以后用在各种处理器中移植该滤波器算法时，可以直接使用。

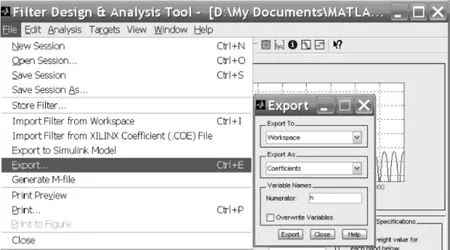
图4 将滤波器作为数组导出

3 实现滤波以及相位同步

3.1 FIR滤波的核心代码

设输入信号为input(n)，长度为M；滤波器数组为h（n）,长度为N，滤波后的输出为output（n）。FIR实现滤波的核心代码为：

图5 原始数据及低通滤波后的数据

3.2 FIR滤波实现相位同步

卷积实现滤波会有一定的相位延迟，但由于是FIR滤波，相位是严格可控的。设输入信号input(n)的长度为M，系统函数h(n)的阶数为N(长度为N+1)，卷积之后得到输出y(n)的长度为M+N，其中相位滞后N/2个点。根据式（4）得知去掉头部N/2个点后取M个点，即可实现输出与输入同相位。

4 运算速度分析以及优化

上述滤波方法在Samsung公司的44B0处理器中运行结果为：当进行2 000个点的60阶FIR滤波运算，总的运算时间约为108ms。这意味着采集1s钟的数据只需要108ms来进行滤波计算，这对于进行滤波处理运算速度是足够的，但如果该嵌入式系统的采样频率更高时，或者还有更多的事情要做时，减少运算时间就显得更有必要。

4.1 从算法原理进行优化

根据FIR滤波器原理［4］，系统函数描述如下：

b(r),r=0,1，…，N分别等于该系统的单位抽样响应 h(r),r=0,1,2，…，N。

当h(n)=±h(N-n)时，对应的FIR系统具有线性相位，该滤波器具有对称性。因此线性相位结构就可以少用N/2个循环。那么此时实现滤波运算的核心代码便可以改为：

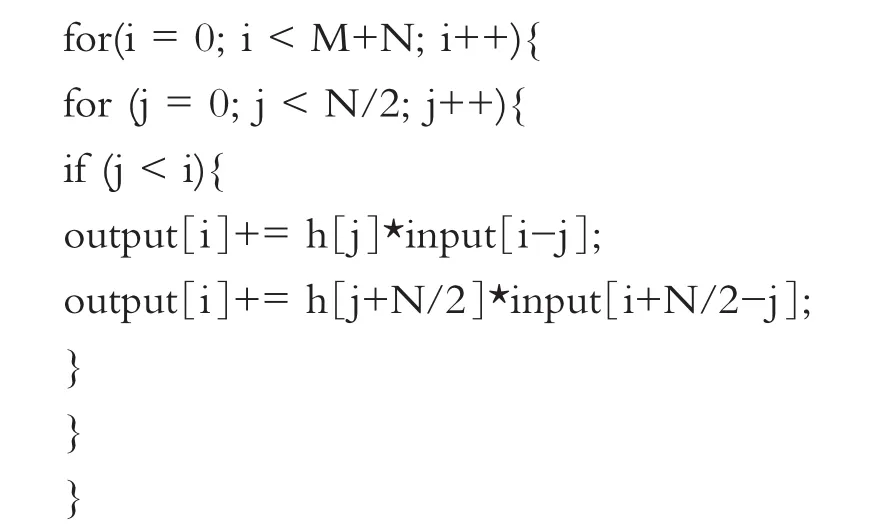
上述的运算代码比优化前的代码少了一半的循环运算，显然提高了运算速度。将上述m语言代码移植到Samsung公司的44B0处理器中运行2 000个点的60阶FIR滤波，需要的时间便由此前的108ms降至72ms左右，明显提高了运算速度。

4.2 对C语言代码进行优化

在嵌入式C语言中，对于数据量大的数组采用指针来进行计算可明显提高运算速度。为了提高运行效率，将这三个数组全改为指针运算，经过示波器测试观察，运行时间约为52ms。这跟优化前的108ms相比，执行效率提高了1倍。

5 其他通带类型滤波器设计

其滤波器的设计跟上述低通滤波器的实现过程是一致的，在这里简要地以设计带通滤波器来予以说明。

根据图2的分析结果，表明该原始信号在100～150Hz之间有一个较大的频率分量，如果我们需要分析该分量的时域波形，就可以用一个带通滤波器来实现。确定带通的参数以及滤波器的幅频特性如图6所示。

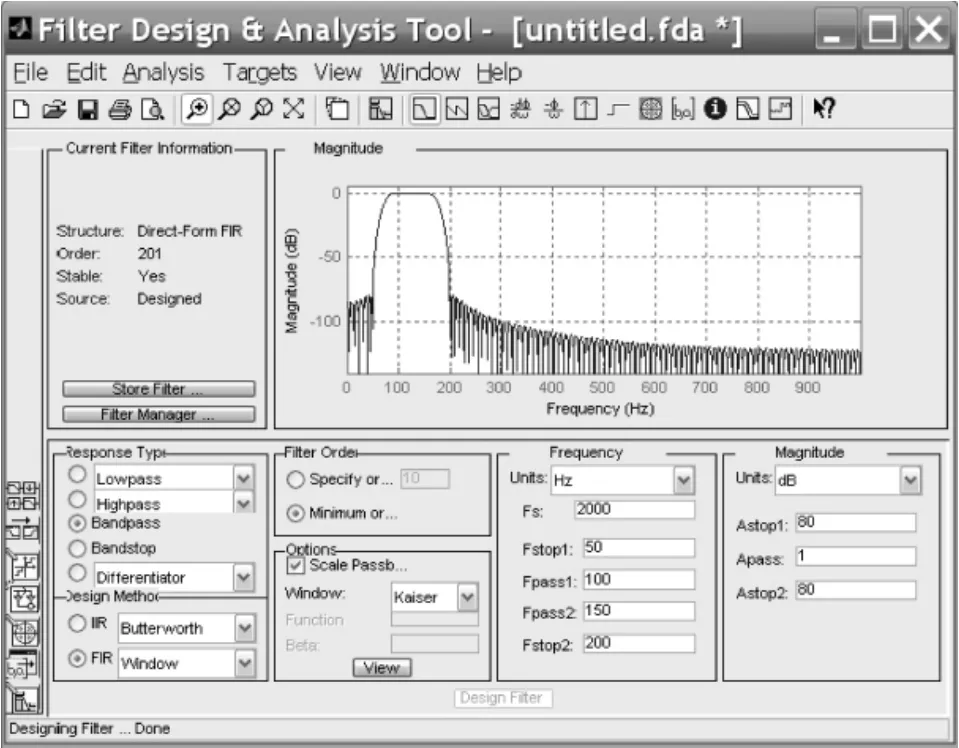
图6 满足要求的FIR带通滤波器的频谱

根据图6生成的滤波器，将滤波器作为数组导出及后续的实现滤波计算与前面讲述的低通滤波过程完全相同，这里不做赘述。原始信号经过带通的数据如图7所示。

从图7可以看出，当信号经过带通滤波器后，直流分量、低频分量和高频分量都已经被滤除掉，整个信号的包络呈现出规律的衰减趋势，这已经达到了滤波效果。

图7 原始数据带通滤波后的效果

6 结 论

本文所设计的FIR滤波能无相位失真地满足滤波效果，在单片机中进行C语言移植后，其运算速度能满足在嵌入式系统中的应用要求。本文提出的实现方法，对于FIR滤波在其他嵌入式系统中的应用提供了一定的借鉴作用。

[1]西蒙·赫金.信号与系统[M].北京：电子工业出版社，2004.

[2]程佩青.数字信号处理教程:第3版[M].北京：清华大学出版社，2007.

[3]王彬.MATLAB数字信号处理[M].北京：机械工业出版社，2010.

[4]胡广书.数字信号处理——理论、算法与实现:第2版[M].北京：清华大学出版社，2003.

Realization and Optimization of FIR Filters in Embedded System

YANG Xiupeng
(Guizhou Space Control Technology Co.,LTD,Guiyang 550009)

This paper introduces basic principle and the linear phase condition of the FIR filters,and the generation of the FIR filters with MATLAB tools is elaborated.The transplanting of the FIR filters getting from MATLAB is completed in embedded system,and computational optimization is achieved.By the processing of noisy data,the method proposed in this paper can meet requirements of engineering practice.

FIR filters；MATLAB；embedded system；computational optimization

TP302

A

1673-1980(2012)05-0154-04

2012-05-03

杨秀朋（1983-），男，土家族，贵州思南人，硕士，研究方向为油田测试设备的信号处理。